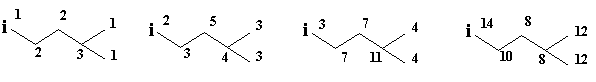Topological Substituent Descriptors
Mircea V. DIUDEA1*, Lorentz JÄNTSCHI2, Ljupčo PEJOV3
1Babeş-Bolyai University Cluj-Napoca, Romania
2 Technical University Cluj-Napoca, Romania
3Sv. Kiril i Metodij University Skopje, Macedonia
*corresponding author, diudea@chem.ubbcluj.ro
Abstract
Motivation. Substituted 1,3,5-triazines are known as useful herbicidal substances. In view of reducing the cost of biological screening, computational methods are carried out for evaluating the biological activity of organic compounds. Often a class of bioactives differs only in the substituent attached to a basic skeleton. In such cases substituent descriptors will give the same prospecting results as in case of using the whole molecule description, but with significantly reduced computational time. Such descriptors are useful in describing steric effects involved in chemical reactions.
Method. Molecular topology is the method used for substituent description and multi linear regression analysis as a statistical tool.
Results. Novel topological descriptors, XLDS and Ws, based on the layer matrix of distance sums and walks in molecular graphs, respectively, are proposed for describing the topology of substituents linked on a chemical skeleton. They are tested for modeling the esterification reaction in the class of benzoic acids and herbicidal activity of 2-difluoromethylthio-4,6-bis(monoalkylamino)-1,3,5-triazines.
Conclusions. Ws substituent descriptor, based on walks in graph, satisfactorily describes the steric effect of alkyl substituents behaving in esterification reaction, with good correlations to the Taft and Charton steric parameters, respectively. Modeling the herbicidal activity of the seo of 1,3,5-triazines exceeded the models reported in literature, so far.
Keywords
Steric effect, Substituent descriptors, Molecular topology, Herbicidal activity.
Abbreviations and notations
MLR, multi linear regression; SVTI, substituent volume topological index; Es, Tafts steric parameter; n, Chartons steric parameter.
1. Introduction
In the field of chemical reactivity, the first proposal of a substituent steric parameter is due to Taft [1, 2]. He tried to quantify the steric influence of a substituent located on the hydrocarbon part of organic esters in the acid-catalysed hydrolysis of aliphatic carboxylic esters, RCOOR. His Es steric parameter is defined as:
![]() (1)
(1)
where ![]() is the ratio of acid-catalysed hydrolysis
rate constant of RCOOR to that of MeCOOR. By definition,
is the ratio of acid-catalysed hydrolysis
rate constant of RCOOR to that of MeCOOR. By definition, ![]() .
.
The Es parameter has been defined empirically [3]. Taft himself pointed out that Es varies parallel to the atom group radius. Charton also found that Es is linearly dependent on the van der Waals radius of the substituent, thus defining a new steric parameter, n [4-8].
Murray [9] found correlations between the Taft parameter and the Randić [10] topological index, for a series of substituted alkyls. In this respect, Ivanciuc and Balaban [3] have proposed a topological descriptor, SVTI, which encodes the topological distances (i.e., the number of bonds/edges, Dij, joining the atoms/vertices i and j on the shortest path) in a molecular graph, G.
It is defined on the fragment F (i.e. an alkyl group) attached to the vertex i of G, as:
![]() (2)
(2)
The summation runs over all NF vertices of F and the distance Dij is limited to 3, in agreement to the Chartons conclusion about the limit of the influence of the steric effect beyond the gamma carbon [5-8].
The calculation of SVTI is exemplified for the sec-butyl group (R = H) or higher homologues (R ¹ H):
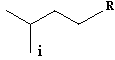
SVTI (s-Bu) = 1+ 2 + 2 + 3 = 8
The above authors have tested their descriptors in describing the reaction rates of acid-catalysed hydrolysis of RCOOR' (the Taft's set).
In the present work, two novel descriptors for substituents are proposed. They are now tested in modeling the effector-receptor interaction in the herbicidal activity of 2-difluoromethylthio-4,6-bis(monoalkylamino)-1,3,5-triazines.
2. Substituent Topological Descriptors, XLDS and Ws
The substituent descriptors XLDS and Ws herein proposed are constructed with the aid of layer matrices.
Before defining our descriptors, lets recall some knowledges about the layer matrices [11-17].
A partition G(i) with respect to the vertex i, in a graph, is defined [11, 14, 15] as:
![]() (3)
(3)
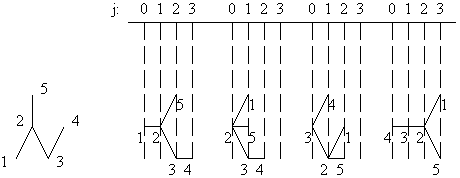
where Diu is the topological distance (see above) and ecci is the eccentricity of i (i.e. the largest distance between i and any vertex in G). Figure 1 illustrates the relative partitions for the graph G1.
Let ![]() be the layer j of
the vertices u located at distance j, in the relative partition G(i):
be the layer j of
the vertices u located at distance j, in the relative partition G(i):
![]() (4)
(4)
The entries in a layer
matrix, LM, collect the topological property Pu for
all vertices u belonging to the layer ![]() :
:
![]() (5)
(5)
|
G1 |
G1(1,5) |
G1(2) |
G1(3) |
G1(4) |
G1(1) = {{1},{2},{3,5},{4}}; G1(2) = {{2},{1,3,5},{4}};
G1(3) = {{3},{2,4},{1,5}}; G1(4) = {{4},{3},{2},{1,5}};
G1(5) = {{5},{2},{1,3},{4}}.
Figure 1. Partitions of G1 with respect to each of its vertices
The matrix LM can be written as:
LM(G)
=![]() (6)
(6)
where V(G) is the set of vertices in graph and d(G) is the diameter (i.e., the largest distance) of G. The dimensions of such a matrix are N´ (d(G)+1).
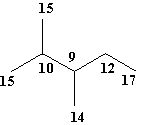
Figure 2 illustrates the layer matrix of distance sums, LDS [13], the topological property M which collects being the sum of distances joining a vertex i with all the remainder vertices in G. Note that the first column contains just the vertex topological property.
(in this case, ![]() , marked in the weighted graph, G2{DSi}).
, marked in the weighted graph, G2{DSi}).
|
G2 |
i \ j: 0 1 2 3 4 |
|
(1) 15 10 24 26 17 (2) 10 39 26 17 0 (3) 9 36 47 0 0 (4) 12 26 24 30 0 (5) 17 12 9 24 30 (6) 15 10 24 26 17 (7) 14 9 22 47 0 LDS(G2) |
Figure 2. Matrix LDS for the graph G2
This matrix and the invariants calculated on (e.g., the well-known Wiener index [18], counting all distances in G) are useful tools in topological description of molecular graphs [13, 14].
Another interesting matrix is the layer matrix of walk degrees [15], LeW. A walk, W, is defined [19] as a continuous sequence of vertices, v1, v2, ..., vm; it is allowed edges and vertices to be revisited.
If the two terminal vertices coincide (v1 = vm ), the walk is called a closed (or self returning) walk, otherwise it is an open walk.
If its vertices are distinct, the walk is called a path. The number e of edges traversed is called the length of walk.
Walks of length e, starting at the vertex i, eW(i), can be counted by summing the entries in the row i of the eth power of the adjacency matrix A (whose nondiagonal entries are 1 if two atoms are adjacent and zero otherwise):
![]() (7)
(7)
where eW(i) is called the walk degree (of rank e) of vertex i (or atomic walk count [15, 20] ).
Walk degrees, eW(i), can be also calculated by summing the first neighbours degrees of lower rank, according to an additive algorithm11 illustrated in figures 3 and 4.
Local and global invariants based on walks in graph were considered for correlating with physico-chemical properties [15, 20].
Figure 3 illustrates the layer matrix of walk degrees, LeW, e = 1-4, for G2. Note that the first column in L1W is just the vertex degree or the vertex valency. Note that the matrix LeW was re-invented by Randic in 2001, for e = 1, under the name valence shells [21].
The substituent descriptor XLDS is the local centrocomplexity index, XLM [14], defined on the LDS matrix:
![]() (8)
(8)
where i is the attachment point of the substituent to a given chemical structure (see figure 4) and z denotes the number of bits of max[LDS]ij in G. Calculation of XLDS is exemplified in figure 4.
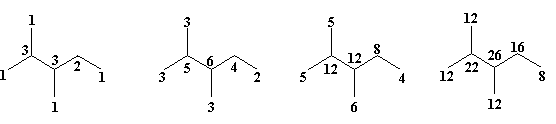
G2 {1Wi } G2 {2Wi } G2 {3Wi } G2 {4Wi }
|
L1W |
L2W |
L3W |
L4W |
i \ j 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4 0 1 2 3 4
1 1 3 4 3 1 3 5 9 7 2 5 12 17 14 4 12 22 38 28 8
2 3 5 3 1 0 5 12 7 2 0 12 22 14 4 0 22 50 28 8 0
3 3 6 3 0 0 6 12 8 0 0 12 26 14 0 0 26 50 32 0 0
4 2 4 4 2 0 4 8 8 6 2 8 16 18 10 0 16 34 34 24 0
5 1 2 3 4 2 2 4 6 8 6 4 8 12 18 10 8 16 26 34 24
6 1 3 4 3 1 3 5 9 7 2 5 12 17 14 4 12 22 38 28 8
7 1 3 5 3 0 3 6 9 8 0 6 12 20 14 0 12 26 38 32 0
Figure 3. Layer matrix of walk degrees, LeW for the graph G2
(calculated by summing the first neighbor degrees of lower rank)
|
{1W} |
{2W} |
{3W} |
{DS} |
(a) |
Ws (i) = 7+7/2+11/3+8/4 ≈ 16.167;
XLDS(i) = 14∙100+10∙10-2+8∙10-4+8∙10-6+12∙10-8+12∙10-10 = 14.1008081212 ≈ 14.101; (b)
Figure 4. (a) Walk degrees, eW, (calculated by summing the first neighbors degrees
of lower rank) and distance sums, DS; (b) Evaluation of Ws and XLDS descriptors
Ws is based on the walks in a connected molecular graph. It is calculated from the layer matrix L3W by:
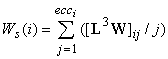 (9)
(9)
where 3W is the walk number, of length 3.
We limited here to elongation 3 by following the Chartons suggestion about the limit of the influence of steric effect (see above). The calculation of the parameter Ws is exemplified in figure 4.
The XLDS descriptor is similar to the SVTI parameter, both of them counting distances in the substituent.
Ws describes the branching in the vicinity of the attachment point i.
All these parameters suggest the steric influence of a substituent in the interaction of the skeleton (or a situs of it) with a partner (e.g., a reactant [3, 22] or a biological receptor). They are free of electronic contributions, at least in the variant in which the heteroatom is not considered.
3. Correlating Test
The utility of the substituent descriptors, XLDS and Ws, was proven on a set of thirty aminoalkyl fragments (table 1) involved in the inhibition of Hill reaction of triazines [23] (figure 5).
In this respect, the fragmental volumes, V, (in cm3/mol) for the considered substituents have been calculated as described below. Other parameter herein considered was the number of atoms different from hydrogen, N.
All these descriptors have been calculated separately for the two sites, A and B (see figure 5).
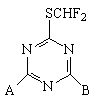
Figure 5. Herbicidal bioactive triazines
Table 1. Topological descriptors and biological activity pI50 for the triazines in figure 5
|
No |
A |
B |
NA |
NB |
Ws, A |
Ws, B |
XA * |
XB |
VA ** |
VB |
pI50 |
|
1 |
NH2 |
NH2 |
1 |
1 |
1 |
1 |
1.1 |
1.1 |
18.763 |
18.763 |
3.82 |
|
2 |
NH2 |
NHCH3 |
1 |
2 |
1 |
5 |
1.1 |
3.23 |
18.763 |
32.636 |
5.20 |
|
3 |
NH2 |
NHC2H5 |
1 |
3 |
1 |
8.5 |
1.1 |
6.446 |
18.763 |
47.908 |
5.34 |
|
4 |
NH2 |
NH-i-C3H7 |
1 |
4 |
1 |
13.66 |
1.1 |
9.061 |
18.763 |
60.766 |
5.83 |
|
5 |
NHCH3 |
NHCH3 |
2 |
2 |
5 |
5 |
3.23 |
3.23 |
32.636 |
32.636 |
6.01 |
|
6 |
NHCH3 |
NHC2H5 |
2 |
3 |
5 |
8.5 |
3.23 |
6.446 |
32.636 |
47.908 |
6.39 |
|
7 |
NHCH3 |
NHC3H7 |
2 |
4 |
5 |
11.75 |
3.23 |
10.071 |
32.636 |
62.393 |
6.75 |
|
8 |
NHCH3 |
NH-i-C3H7 |
2 |
4 |
5 |
13.66 |
3.23 |
9.061 |
32.636 |
60.766 |
6.76 |
|
9 |
NHCH3 |
NHC4H9 |
2 |
5 |
5 |
13.93 |
3.23 |
15.111 |
32.636 |
76.638 |
6.74 |
|
10 |
NHCH3 |
NH-s-C4H9 |
2 |
5 |
5 |
15.16 |
3.23 |
13.091 |
32.636 |
75.039 |
6.76 |
|
11 |
NHCH3 |
NH-t-C4H9 |
2 |
5 |
5 |
20.50 |
3.23 |
12.081 |
32.636 |
74.106 |
6.78 |
|
12 |
NHCH3 |
NHC5H11 |
2 |
6 |
5 |
15.62 |
3.23 |
21.161 |
32.636 |
88.241 |
7.12 |
|
13 |
NHC2H5 |
NHC2H5 |
3 |
3 |
8.5 |
8.5 |
6.446 |
6.446 |
47.908 |
47.908 |
6.82 |
|
14 |
NHC2H5 |
NHC3H7 |
3 |
4 |
8.5 |
11.75 |
6.446 |
10.071 |
47.908 |
62.393 |
6.74 |
|
15 |
NHC2H5 |
NH-i-C3H7 |
3 |
4 |
8.5 |
13.66 |
6.446 |
9.061 |
47.908 |
60.766 |
6.89 |
|
16 |
NHC2H5 |
NHC4H9 |
3 |
5 |
8.5 |
13.93 |
6.446 |
15.111 |
47.908 |
76.638 |
6.95 |
|
17 |
NHC2H5 |
NH-i-C4H9 |
3 |
5 |
8.5 |
16.16 |
6.446 |
14.101 |
47.908 |
74.497 |
7.01 |
|
18 |
NHC2H5 |
NH-s-C4H9 |
3 |
5 |
8.5 |
15.16 |
6.446 |
13.091 |
47.908 |
75.039 |
6.87 |
|
19 |
NHC2H5 |
NH-t-C4H9 |
3 |
5 |
8.5 |
20.50 |
6.446 |
12.081 |
47.908 |
74.106 |
6.97 |
|
20 |
NHC2H5 |
NHC5H11 |
3 |
6 |
8.5 |
15.62 |
6.446 |
21.161 |
47.908 |
88.241 |
6.94 |
|
21 |
NHC2H5 |
NHC6H13 |
3 |
7 |
8.5 |
17.00 |
6.446 |
28.222 |
47.908 |
102.032 |
7.21 |
|
22 |
NHC2H5 |
NHC7H15 |
3 |
8 |
8.5 |
18.17 |
6.446 |
36.292 |
47.908 |
116.672 |
7.01 |
|
23 |
NHC2H5 |
NHC8H17 |
3 |
9 |
8.5 |
19.18 |
6.446 |
45.373 |
47.908 |
128.770 |
6.81 |
|
24 |
NHC3H7 |
NHC3H7 |
4 |
4 |
11.75 |
11.75 |
10.071 |
10.071 |
62.393 |
62.393 |
6.45 |
|
25 |
NH-i-C3H7 |
NHC3H7 |
4 |
4 |
13.66 |
11.75 |
9.061 |
10.071 |
60.766 |
62.393 |
6.75 |
|
26 |
NH-i-C3H7 |
NH-i-C3H7 |
4 |
4 |
13.66 |
13.66 |
9.061 |
9.061 |
60.766 |
60.766 |
6.75 |
|
27 |
NH-i-C3H7 |
NHC4H9 |
4 |
5 |
13.66 |
13.93 |
9.061 |
15.111 |
60.766 |
76.638 |
6.71 |
|
28 |
NH-i-C3H7 |
NH-s-C4H9 |
4 |
5 |
13.66 |
15.16 |
9.061 |
13.091 |
60.766 |
75.039 |
6.88 |
|
29 |
NH-i-C3H7 |
NH-t-C4H9 |
4 |
5 |
13.66 |
20.50 |
9.061 |
12.081 |
60.766 |
74.106 |
6.70 |
|
30 |
NH-i-C3H7 |
NHC5H11 |
4 |
6 |
13.66 |
15.62 |
9.061 |
21.161 |
60.766 |
88.241 |
6.69 |
* The symbol X stands for XLDS (see text);
** Volume, [cm3/mol].
Table 2. Statistics of multivariable regression (distinct variables on branches A and B)
|
No. |
XI |
bi |
A |
r |
s |
v(%) |
F |
|
1 |
1/N,B |
-3.786 |
7.549 |
0.8987 |
0.311 |
4.752 |
117.587 |
|
2 |
1/Ws,B |
-3.372 |
6.933 |
0.8298 |
0.396 |
6.047 |
61.899 |
|
3 |
1/XB |
-3.806 |
7.038 |
0.8835 |
0.333 |
5.076 |
99.598 |
|
4 |
1/VB |
-72.276 |
7.760 |
0.8975 |
0.313 |
4.779 |
115.936 |
|
5 |
1/NA 1/NB |
-1.234 -2.678 |
7.810 |
0.9577 |
0.208 |
3.175 |
149.557 |
|
6 |
1/Ws,A 1/Ws,B |
-1.335 -2.077 |
7.118 |
0.9615 |
0.199 |
3.030 |
165.554 |
|
7 |
1/XA 1/XB |
-1.317 -2.526 |
7.252 |
0.9662 |
0.186 |
2.844 |
189.755 |
|
8 |
1/VA 1/VB |
-22.999 -52.514 |
8.048 |
0.9478 |
0.231 |
3.519 |
119.237 |
|
9 |
1/Ws,A 1/VB |
-1.114 -47.194 |
7.618 |
0.9714 |
0.172 |
2.619 |
226.162 |
|
10 |
1/Ws,A 1/XB |
-1.180 -2.458 |
7.159 |
0.9729 |
0.167 |
2.550 |
239.280 |
|
11 |
1/Ws,A 1/NB |
-1.120 -2.484 |
7.484 |
0.9746 |
0.162 |
2.472 |
255.491 |
|
12 |
NA 1/NA 1/NB |
-0.385 -2.777 -2.444 |
9.477 |
0.9834 |
0.134 |
2.039 |
254.937 |
|
13 |
Ws,A 1/Ws,A 1/Ws,B |
-0.025 -1.594 -2.056 |
7.372 |
0.9661 |
0.190 |
2.903 |
121.327 |
|
14 |
XA 1/XA 1/XB |
-0.078 -2.047 -2.413 |
7.876 |
0.9818 |
0.140 |
2.132 |
232.401 |
|
15 |
VA 1/VA 1/VB |
-0.036 -65.998 -45.367 |
10.649 |
0.9808 |
0.144 |
2.193 |
219.227 |
|
16 |
XA 1/VA 1/VB |
-0.155 -59.011 -46.244 |
9.762 |
0.9815 |
0.141 |
2.152 |
228.039 |
|
17 |
XA 1/VA 1/XB |
-0.154 -60.818 -2.399 |
9.337 |
0.9836 |
0.133 |
2.029 |
257.426 |
|
18 |
XA 1/VA 1/NB |
-0.153 -58.888 -2.430 |
9.614 |
0.9846
|
0.129 |
1.968 |
274.318 |
In table 2 A and bi values are the coefficients of:
![]() (10)
(10)
and leave one out procedure (loo) has the results:
loo(12): r = 0.9768; s = 0.153; v(%) = 2.332;
loo(18): r = 0.9778; s = 0.149; v(%) = 2.271. (11)
The inhibitory activities of triazines on Chlorella have been taken from the study of Morita et al [24]. They are expressed as pI50, which represents the negative logarithm of concentration required for 50% inhibition of Hill reaction. The correlating results are listed in table 2.
4. Results and Discussion
In single variable regression, the descriptors for the substituents in branch B (table 2) are not satisfactory to model the inhibitory activity of triazines; the correlation coefficient, r, is lower than 0.9 (for those in A, r is still lower) and the coefficient of variance, v, is about 5 %. Note that all these "steric" descriptors are taken as reciprocal values, suggesting that the triazine ring fits at the biological receptor as better as the substituent is less sterically involved.
In two variables regression, by adding the descriptors for the branch A the correlation is improved, as indicates the higher values for r and F (the Fisher ratio) and the drop in the dispersion, s, and v(%) values (entries 5-8, table 2). When the descriptors for the two branches are heterogeneous, the result is still better (entries 9-11).
In three variables regression, the correlation is once more improved. Again the heterogeneous descriptors model the inhibition reaction better that the homogeneous ones (compare entries 16-18 with 12-15, Table 2).
The best model found (see also entry 18) was:
pI50 = 9.614 0.153∙XA 58.888∙1/VA 2.430∙1/NB;
n = 30; r2 = 0.9694; s = 0.129; v(%) = 1.968; F = 274.3; (10)
The cross validation (leave-one-out, loo, procedure) test for the equations in entries 12 and 18 are given in the bottom of table 2.
Despite the excellent model offered by equation (10), a brief inspection on the general structure of these triazines showed a rather surprising error: the molecule is symmetric, so that the two branches A and B are interchangeable! In consequence, the two columns of descriptors have no meaning if they are taken as distinct descriptors. Thus, the contribution of the substituents in A and B in modeling the global biological activity must somehow be mixed!
The simple summation (or simple arithmetic mean) of contributions of the two branches, A and B, did not provide satisfactory results. More reliable appeared in other kinds of average: geometric (geo) and harmonic (har). The best correlating results are included in table 3. The cross validation test, loo, is given for each entry.
From table 3 it appears that, in single variable regression, the descriptor 1/X(LDS)geo provides a rather good (r> 0.95) description of the activity, both in estimation and prediction, "loo" (entry 2).
The best prediction is offered by the three variables equation, in entry 6 (r >0.975), all of them as harmonic average of the descriptors of A and B branches:
pI50 = 10.292 119.503∙1/Vhar 0.097∙Xhar 0.047∙Ws,har;
n = 30; r = 0.9807; s = 0.144; v(%) = 2.198; F = 218.158; (11)
The corresponding arithmetic averaged descriptors used in (11) supplied a correlation of r = 0.955 which is, of course, unsatisfactory.
This equation was chosen for a tempting prediction in the past. The experimental data for the compounds no. 3, 12, 21 and 24 (showing residuals, ycalc-yexp, about two times or larger than the value of standard error of estimate:
s = +0.144; -0.254; +0.236; +0.301 and -0.398, respectively
were changed by the values:
5.6209; 6.8778; 6.9073 and 6.8471, respectively
calculated by equations:
pI50 = 10.292 119.503 1/Vhar 0.097 Xhar 0.047 Ws,har
n = 26; r = 0.9932; s = 0.086; v(%) = 1.309; F = 530.484 (12)
The correlating data, obtained by using the new column of activities, ycor, are included in table 3 as the rows "ycor". The improvement in the statistical parameters of the regression equations is obvious for all data of table 3 (where * means "leave one out" cross validation procedure; and ** are yi corrected for i = 3, 12, 21 and 24):
Table 3. Statistics of multivariable regression, Ycalc = a + åi biXi (averaged variables)
|
No. |
Xi |
bi |
a |
r |
s |
v(%) |
F |
|
1 |
1/Ws,har loo* ycor** |
-3.151
|
7.121
|
0.9553 0.9467 0.9666 |
0.210 0.229 0.175 |
3.204 3.489 2.669 |
292.215
398.721 |
|
2 |
1/Xgeo loo ycor |
-3.891
|
7.253
|
0.9621 0.9558 0.9793 |
0.194 0.209 0.138 |
2.956 3.183 2.108 |
348.097
655.776 |
|
3 |
1/Vhar Nhar loo ycor |
-126.800 -0.541
|
11.091 |
0.9763
0.9721 0.9924 |
0.156
0.167 0.086 |
2.387
2.543 1.307 |
275.063
875.466 |
|
4 |
1/Vhar Xhar loo ycor |
-113.340 -0.137 |
10.010 |
0.9777
0.9735 0.9907 |
0.152
0.163 0.095 |
2.318
2.480 1.446 |
292.278
713.286 |
|
5 |
1/Nhar Xhar Ws,har loo ycor |
-5.614 -0.056 -0.057 |
9.491 |
0.9798
0.9742 0.9918 |
0.147
0.160 0.091 |
2.247
2.446 1.380 |
208.342
523.336 |
|
6 |
1/Vhar Xhar Ws,har loo ycor |
-119.503 -0.097 -0.047 |
10.292 |
0.9807
0.9752 0.9938 |
0.144
0.157 0.079 |
2.198
2.397 1.204 |
218.158
690.328 |
|
7 |
1/Vhar Xhar Ws,har Nhar loo ycor |
-105.131 -0.232 -0.081 0.673 |
9.058 |
0.9824
0.9742 0.9938 |
0.141
0.160 0.080 |
2.144
2.444 1.226 |
172.608
499.253 |
|
8 |
1/Nhar Xhar Ws,har Vhar loo ycor |
-4.724 -0.228 -0.070 0.052 |
7.858 |
0.9825
0.9751 0.9924 |
0.140
0.157 0.089 |
2.139
2.401 1.358 |
173.400
405.773 |
More over, among the 24 descriptors (N, V, Ws, XLDS , 1/N, 1/V, 1/Ws, 1/XLDS, taken as "ari", "har" and "geo" average) used in single variable regression, in 20 of them an improvement of the statistics was recorded. Again the equation in entry 6 was the best model. This test suggested that the experimental data for the compounds, above mentioned, are "in error".
From eq 11 and table 3, it comes out that the inhibitory activity of triazines is controlled by the possibility of the triazine ring (i.e., the pharmacophor) to accommodate at the receptor situs.
This opinion is supported by the reciprocal values and the negative regression coefficient, and negative partial correlation index of these "steric" descriptors involved in an eq. of type 11. It suggests that the triazine ring fits at the biological receptor as better as the substituent is less sterically involved.
A plot of the observed vs. calculated (by eq 11) pI50 values is given in figure 6. For comparison, the plot for the same descriptors and ycor is given in Figure 7.
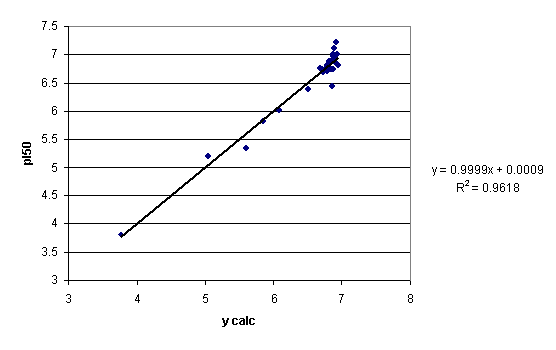
Figure 6. Plot of experimental biological activity (VAR1) vs. ycalc. (cf. eq 11) values
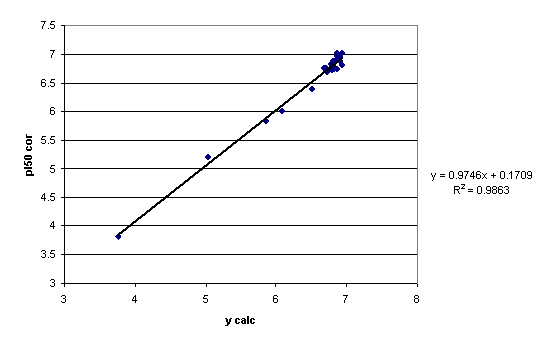
Figure 7. Plot of experimental biological activity (VAR1) vs. ycor values
4. Computation of Fragmental Volumes
The geometries of the hydrocarbon fragments (in fact, the corresponding radicals) were fully optimized at the Unrestricted Hartree-Fock (UHF) level of theory, using the 6-31G** basis set (of DZP quality), which contains a single set of d polarization functions on carbons, and a single set of p polarization functions on hydrogens for better description of the radical wavefunctions.
The Berny's optimization algorithm was used (the energy derivatives with respect to nuclear coordinates were computed analytically [25]), along with the initial guess of the second derivative matrix.
Standard harmonic vibrational analysis was applied to test the character of the optimized geometries (stationary points at the potential energy hypersurfaces - PES). All stationary points corresponded to real minima on the explored PES.
Molecular volume calculations were performed for the optimized structures, by the Monte-Carlo method. Since Monte-Carlo method for calculating molecular volume (defined as the volume inside a contour of 0.001 electrons/Bohr3 density) is stochastically based algorithm, it often leads to results accurate up to several percents.
Therefore, 11 volume calculations per fragment were performed for each fragment, and the arithmetic average value was taken as the closest approximation to the real one (at the level of theory employed).
In order to increase the density of points for a more accurate integration, the "Tight" option of the Gaussian "Volume" keyword was used. All calculations were performed with Gaussian 94 suite of programs [26].
5. Conclusions
The Ws descriptor, based on the walks in graph, satisfactorily describes the steric effect of alkyl substituents in the esterification reaction.
It is a pure steric parameter, not affected by the electronic effects. Ws correlate well to the fragmental volumes (over 0.92) and show a lower degeneracy in comparison to the SVTI, n and Nc parameters.
It is also well correlated18 to the Taft, Es, (0.9637), and Charton, n, (0.9587), parameters, which makes from Ws a promising alternative in describing the steric effect of alkyl substituents.
6. Acknowledgment
The work was supported in part by the Romanian GRANT CNCSIS 2002.
References
[1] R. W. Taft, Linear free energy relationships from rates of esterification and hydrolysis of aliphatic and ortho-substituted benzoate esters. J. Am. Chem. Soc. 1952, 74, 2729-2732.
[2] R. W. Taft, Polar and steric substituent constants for aliphatic and o-benzoate groups from rates of esterification and hydrolysis of esters. J. Am. Chem. Soc. 1952, 74, 3120-3128.
[3] O. Ivanciuc and A. T. Balaban, A new topological parameter for the steric effect of alkyl substituents. Croat. Chem. Acta, 1996, 69, 75-83.
[4] M. Charton, The nature of the ortho effect. II. Composition of the Taft steric parameters. J. Am. Chem. Soc. 1969, 91, 615-618.
[5] M. Charton, Steric effects. I. Esterification and acid-catalyzed hydrolysis of esters. J. Am. Chem. Soc. 1975, 97, 1552-1556.
[6] M. Charton, Steric effects. II. Base-catalyzed ester hydrolysis. J. Am. Chem. Soc. 1975, 97, 3691-3693.
[7] M. Charton, Steric effects. III. Bimolecular nucleophilic substitution. J. Am. Chem. Soc. 1975, 97, 3694-3697.
[8] M. Charton, Steric effects. IV. E1 and E2 eliminations. J. Am. Chem. Soc. 1975, 97, 6159-6161.
[9] W. J. Murray, J. Pharm. Sci. 1977, 66, 1352.
[10] M. Randić, On characterization of molecular branching. J. Am. Chem. Soc. 97 (1975) 6609-6615.
[11] V. A. Skorobogatov and A. A. Dobrynin, Metric analysis of graphs. Commun. Math. Comput. Chem (MATCH) 1988, 23, 105-151.
[12] M. V. Diudea, O. M. Minaliuc and A. T. Balaban, Regressive Vertex Degrees (New Graph Invariants) and Derived Topological Indices. J. Comput. Chem., 1991, 12, 527-535.
[13] T. Balaban and M. V. Diudea, Real Number Vertex Invariants: Regressive Distance Sums and Related Topological Indices. J. Chem. Inf. Comput. Sci., 1993, 33, 421-428.
[14] M. V. Diudea, Layer Matrices in Molecular Graphs. J. Chem. Inf. Comput. Sci. 1994, 34, 1064-1071.
[15] M. V. Diudea, M. I. Topan and A. Graovac, Layer Matrices of Walk Degrees. J. Chem. Inf. Comput. Sci. 1994, 34, 1072-1078.
[16] C. Y. Hu, L. Xu, A new algorithm for computer perception of topological symmetry. Anal. Chim. Acta 1994, 295, 127-134.
[17] Ch. Y. Hu, L. Xu, On highly discriminating molecular topological index. J. Chem. Inf. Comput. Sci. 1996, 36, 82-90.
[18] H. Wiener, Structural determination of parafin boiling point. J. Am. Chem. Soc., 1947, 69, 17-20.
[19] N. Trinajstić, Chemical Graph Theory; CRC Press, Inc.; Boca Raton, FL, 1983.
[20] G. Rücker, C. Rücker, Counts of all walks as atomic and molecular descriptors. J. Chem. Inf. Comput. Sci. 1993, 33, 683-695.
[21] M. Randić, Graph valence shells as molecular descriptors. J. Chem. Inf. Comput. Sci. 2001, 41, 627-630.
[22] C. M. Pop, M. V. Diudea and L. Pejov, Taft Revisited, Studia Univ."Babes-Bolyai", 1997, 42, 131-138.
[23] M. okić, D. Plavić, N. Trinajstić, 2-Difluoromethylthio-4,6-bis(monoalkylamino)-1,3,5-triazines as inhibitors of Hill reaction: a QSAR study with orthogonalized descriptors. J. Chem. Inf. Comput. Sci. 1996, 36, 146-150.
[24] K. Morita, T. Nagare, Y. Hayashi, Quantitative structure-activity relationships for herbicidal 2-Difluoromethylthio-4,6-bis(monoalkylamino)-1,3,5-triazines Agric. Biol. Chem., 1987, 51, 1955-1957.
[25] H. B. Schlegel, Optimization of Equilibrium Geometries and Transition Structures, J. Comp. Chem., 1982, 3, 214-220.
[26] M. J. Frisch, G. W. Trucks, H. B. Schlegel, P. M. W. Gill, B. G. Johnson, M. A. Robb, J. R. Cheeseman, T. A. Keith, G. A. Petersson, J. A. Montgomery, K. Raghavachari, M. A. Al-Laham, V. G. Zakrzewski, J. V. Ortiz, J. B. Foresman, C. Y. Peng, P. Y. Ayala, M. W. Wong, J. L. Andres, E. S. Replogle, R. Gomperts, R. L. Martin, D. J. Fox, J. S. Binkley, D. J. Defrees, J. Baker, J. P. Stewart, M. Head-Gordon, C. Gonzalez, and J. A. Pople, Gaussian 94 (Revision B.3), Gaussian, Inc., Pittsburgh PA, 1995.