Graph Theory.
1. Fragmentation of Structural Graphs
Lorentz JÄNTSCHI
Technical University Cluj-Napoca
Abstract
The investigation of structural graphs has many fields of applications in engineering, especially in applied sciences like as applied chemistry and physics, computer sciences and automation, electronics and telecommunication.
The main subject of the paper is to express fragmentation criteria in graph using a new method of investigation: terminal paths. Using terminal paths are defined most of the fragmentation criteria that are in use in molecular topology, but the fields of applications are more generally than that, as I mentioned before.
Graphical examples of fragmentation are given for every fragmentation criteria. Note that all fragmentation is made with a computer program that implements a routine for every criterion.[1]
A web routine for tracing all terminal paths in graph can be found at the address: http://vl.academicdirect.ro/molecular_topology/tpaths/.
Keywords
Graph theory, Graph fragmentation, Vertex descriptors, Molecular topology, Graph coloring, Graph partitioning.
1. Introduction
The fragmentation of structural graphs has various applications, starting from electric circuits and internet routing and ending with computational chemistry and molecular topology.
Partitioning of graph in classes of vertices may be done in different ways [2],[3]. The most frequently used discriminating criteria are well-known square matrices that collect contributions of pairs of vertices from the graph. The adjacency matrix is the simplest matrix of this type.
Some authors use characteristic polynomial and its eigenvalue to characterize a given graph [4].
The sequence of eigenvalues forms the graph spectrum [5]. A basic result in spectral geometry is the theorem of Cheng [6].
Let us consider a sequence matrix. It is of dimension n×(n-1), where n is the number of vertices.
Such a matrix can be used to compare different graphs (interstructural similarity), when analyzing the columns of sequence matrices, the sums by columns or global sums (generic indices) [7].
It is also possible to compare the vertices of a graph (intrastructural similarity), when analyzing the rows of sequence matrices and the sums by rows [8],[9]. With this observation, a sequence matrix is an elegant method to investigate graphs [10].
Note that the ordering of graph vertices by using sequence matrices is of a partially ordered type [11],[12].
Prior, Dobrynin reported the degeneracy of some sequence matrices [13],[14]. Decomposition of graphs into congruent factors has interesting chemical implications [15],[16]. Dobrynin [17] and Diudea [18],[19] reported distance degree sequences (DPS in our notation) and their chemical applications.
The path sequence matrix (APS in our notation) is calculated in order to study molecular similarity [20].
2. Terminal Paths
Let G = (V, E) be an un-oriented graph. We are note the set of all paths in G with P(G). The distance from i to j in G is d(G)i,j and detour is δ(G)i,j. For p Î P(G), l(p) denotes the length of path p.
|
t = (vi)1≤i≤n is named terminal path if: vi Î V, t Î P(G) and "v Î V s. th. (vn, v) Î E then t È (vn, v) Ï P(G) |
(1) |
The set of terminal paths in G is T(G) = (T(G)v)vÎV where T(G)i is:
|
T(G)i = {t = (vi)1≤i≤n s. th. v1 = i and t terminal path} |
(2) |
Note that if G = (V, E) is a connected graph, then " v Î V, " e Î E $ t Î T(G)v s. th. e Í t. Thus, any connected graph can be reconstructed from the terminal path list starting from an arbitrary vertex.
Also, " i, j Î V, T(G)j can be constructed from T(G)i. Consequently, the sets of terminal paths T(G)v, v Î V are equivalent by construction.
For exemplification of terminal paths, let us consider the graph G from fig. 1:

Fig. 1. Graph G
G = (V, E); V = {1, …, 8}; E = {(1, 2), (1, 3), (2, 4), (3, 5), (3, 6), (4, 5), (4, 7), (6, 7), (7,8)}
All terminal paths starting from vertex 1 are computed using graph G from figure 1 and definitions (1) and (2). The solution is:
|
T(G)1 = {
} |
{1, 2, 4, 5, 3, 6, 7, 8}, {1, 2, 4, 7, 8}, {1, 2, 4, 7, 6, 3, 5}, {1, 3, 6, 7, 8}, {1, 3, 6, 7, 4, 2}, {1, 3, 6, 7, 4, 5}, {1, 3, 5, 4, 7, 6}, {1, 3, 5, 4, 7, 8}, {1, 3, 5, 4, 2} |
(3) |
Note that according to definition (1) and (2), T(G) Í P(G) for any graph G.
3. Graph Partitioning in Sets
Let G = (V, E) be a connected graph and i, j Î V two vertices. Let p Î P(G)i,j a path from i to j in G.
|
CJi,j,p = {k : k Î V} is named CJ set of i vs. j and p if: d(G)k,i < d(G)k,j $ q Î Pk,i s. th. p Ç q = {i} |
(4) |
The set of sets of vertices CJSi,j = {CJi,j,p : pÎP(G)i,j} are named set of CJ sets of i vs. j.
|
CJDii,j,p = {k : k Î V} is named CJDi set of i vs. j and p if: CJDii,j,p Î CJSi,j l(p) = d(G)i,j |
(5) |
The set of sets of vertices CJDiSi,j = {CJDii,j,p : p Î P(G)i,j} are named set of CJDi sets of i vs. j.
|
CJDei,j,p = {k | k Î V} is named CJDe set of i vs. j and p if: CJDii,j,p Î CJSi,j l(p) = δ(G)i,j |
(6) |
The set of sets of vertices CJDeSi,j = {CJDei,j,p | p Î P(G)i,j} are named set of CJDe sets of i vs. j. CJDiMi,j = {s : s Î CJDiSi,j} is named CJDiM set of i vs. j if l(s) = max{ |cjdi| : cjdi Î CJDiSi,j}. CJDeMi,j = {s : s Î CJDeSi,j} is named CJDeM set of i vs. j if l(s) = max{ |cjde| : cjde Î CJDeSi,j}. The sets CJDi can be constructed as follows:
|
CJDii,j,p = Æ; CJDij,i,p = Æ; For (v = 1; v ≤ |V|; v++) If (d(G)v,i < d(G)v,j) and ($p' Î P(G)v,i s.th. p' Ç p == {i}) then CJDii,j,p = CJDii,j,p È {v}; EndIf; If (d(G)v,j < d(G)v,i) and ($p' Î P(G)v,j s.th. p' Ç p == {j}) then CJDij,i,p = CJDij,i,p È {v}; EndIf; EndFor; |
(7) |
Note that the algorithm (7) can be applied for any distance operator in place of d(∙), such as detour operator δ(∙).
Through CJ sets there exist inclusions relations:
|
CJDiSMi,j Í CJDiSi,j Í CJSi,j and CJDeSMi,j Í CJDeSi,j Í CJSi,j |
(8) |
that are obviously from the definitions (4)-(6). Figurative, inclusions are:
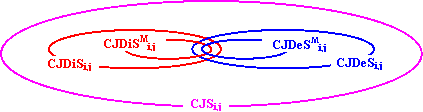
Fig. 2. Inclusions relations in CJ sets
Note that in generally the sets CJDiSMi,j, CJDiSi,j, CJSi,j, CJDeSi,j, CJDeSMi,j are not distinct; more, in trees the sets are equals.
To prove that the sets CJDiSMi,j, CJDiSi,j, CJSi,j, CJDeSi,j, CJDeSMi,j are not banal, let’s apply the algorithm (7) to construct sets for graph G from fig. 1.
Following example shows that sets CJDiSM and CJDeSM are not identically:
CJDiSM1,2 = {CJ1,2,[1,2]}; CJ1,2,[1,2] = {1, 3, 6, 8}
CJDiSM2,1 = {CJ2,1,[2,1]}; CJ2,1,[2,1] = {2, 4, 7}
CJDeSM1,2 = {CJ1,2,[1,3,6,7,4,2]}; CJ1,2,[1,3,6,7,4,2] = {1}
CJDeSM1,2 = {CJ2,1,[2,4,7,6,3,1]}; CJ2,1,[2,4,7,6,3,1] = {2}
and graphical representation of them are in fig. 3:
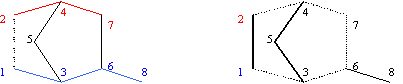
Fig. 3. CJDi and CJDe sets for vertices 1 and 2 and graph G from fig. 1
The following example shows that CJDe sets are not included in CJDi sets:
CJDiSM4,8 = {CJ4,8,[4,7,6,8]}; CJ4,8,[4,7,6,8] = {1, 2, 4, 5}
CJDiSM8,4 = {CJ8,4,[8,6,7,4]}; CJ8,4,[8,6,7,4] = {8}
CJDeSM4,8 = {CJ4,8,[4,2,1,3,6,8]}; CJ4,8,[4,2,1,3,6,8] = {4, 5, 7}
CJDeSM8,4 = {CJ8,4,[8,6,3,1,2,4]}; CJ8,4,[8,6,3,1,2,4] = {8}
and graphical representation of them are in fig. 4:
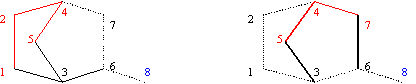
Fig. 4. CJDi4,8,[4,7,6,8] and CJDe4,8,[4,2,1,3,6,8] sets for graph G from fig. 1
The following example shows that sets CJDiSM can contain more than one set:
CJDiSM2,8 = {CJ2,8,[2,4,7,6,8] = {1, 2, 5}, CJ2,8,[2,1,3,6,8] = {4, 2, 5}};
CJDiSM8,2 = {CJ8,2,[8,6,3,1,2] , CJ8,2,[8,6,3,1,2]}; CJ8,2,[8,6,3,1,2] = CJ8,2,[8,6,7,4,2] = {8};
and graphical representation of them are in fig. 5:
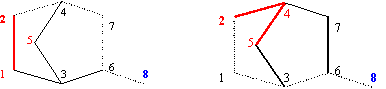
Fig. 5. CJDi2,8,[24768] and CJDi2,8,[21368] sets of graph G from fig. 1
4. Gp Subgraph
Let p = (i = v1, …, vl(p) = j) Î P(G) a path starting from vertex i and ending in vertex j. The Gp subgraph of graph G and path p is defined by:
|
Gp = (Vp, Ep), Vp = {v Î V : v Ï p\{i, j}}, Ep = {e = (ea, eb) Î E : ea, eb Ï p\{i, j}} |
(9) |
Note that Gp subgraph associated of graph G and path p is not necessary a connected subgraf, even if G is a connected graph. More, if G is a tree, Gp has at least two connected components.
For path p = [1, 3, 5, 4, 7] and graph G from fig. 1 the graph G[1, 3, 5, 4, 7] = G\[1, 3, 5, 4, 7] is not a connected graph. Gp has two connected components: [1, 2] and [7, 6, 8]. Also, from original graph G, p\{1,7} is also a connected component. Using comparison operator ≤ between graphs is obviously that Gp È p ≤ G. In fig. 6 are graphically represented the components of G by path p:

Fig. 6. Graph G, path p = [1, 3, 5, 4, 7], path p\{1, 7} = [3, 5, 4] and subgraph Gp
Gp = (Vp, Ep), Vp = {1, 2, 6, 7, 8}, Ep = {(1,2), (6, 7), (6, 8)}
Note that G = Gp È p È [2, 4] È [3, 6].
3. Graph Partitioning in Fragments
Let G = (V, E) be a connected graph and i, j Î V two vertices. Let p Î P(G)i,j a path from i to j in G.
|
CFi,j,p = {k : k Î V} is named CF fragment of i vs. j and p if: d(Gp)k,i < d(Gp)k,j |
(10) |
where subgraph Gp is obtained from graph G and path p according to definition (9).
Note that in definition (10) is used term of fragment for CFi,j,p. Indeed, CFi,j,p is an fragment, a connected set of vertices from graph G.
The set of sets of vertices CFSi,j = {CFi,j,p : p Î P(G)i,j} are named set of CF sets of i vs. j.
More, in CFSi,j,p fragment, there exist the relation:
|
"kÎCFSi,j,p, $qÎP(Gp)k.i path from k to i in Gp s. th. qÇp = {i} |
(11) |
Similar to definitions (5) and (6), CFDi and CFDe fragments are defined:
|
CFDii,j,p={k : kÎV} is named CFDi fragment of i vs. j and p if: CFDii,j,p Î CFSi,j l(p) = d(Gp)i,j |
(12) |
The fragments set CFDiSi,j = {CFDii,j,p : p Î P(G)i,j} are named set of CFDi fragments of i vs. j.
|
CFDei,j,p={k : kÎV} is named CFDe fragment of i vs. j and p if: CFDei,j,p Î CFSi,j l(p) = δ(Gp)i,j |
(13) |
The fragments set CFDeSi,j = {CFDei,j,p : pÎP(G)i,j} are named set of CFDe fragments of i vs. j. CFDiMi,j = {f : f Î CFDiSi,j} is named CFDiM fragment of i vs. j if l(f) = max{ |cfdi| : cfdi Î CFDiSi,j}. CFDeMi,j = {f : f Î CFDeSi,j} is named CFDeM set of i vs. j if l(f) = max{ |cfde| : cfde Î CFDeSi,j}. The sets CFDi can be constructed as follows:
|
CFDii,j,p = Æ; CFDij,i,p = Æ; For (v = 1; v ≤ |V|; v++) If (d(Gp)v,i < d(Gp)v,j) then CFDii,j,p È= {v}; EndIf; If (d(Gp)v,j < d(Gp)v,i) then CFDij,i,p È= {v}; EndIf; EndFor; |
(14) |
Note that the algorithm (14) can be applied for any distance operator in place of d(∙), such as detour operator δ(∙).
Based on construction (14) the sets CFDi are always fragments. Through CF sets it exist inclusions relations:
|
CFDiSMi,j Í CFDiSi,j Í CFSi,j and CFDeSMi,j Í CFDeSi,j Í CFSi,j |
(15) |
that are obviously from the definitions (11)-(13). Figurative, inclusions are:
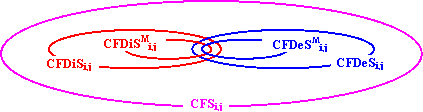
Fig. 7. Inclusions relations for CF sets
Note that in generally the sets CF are not distinct. In trees are even equals.
To prove that the sets CFDiSMi,j, CFDiSi,j, CFSi,j, CFDeSi,j, CFDeSMi,j are not banal, let’s apply the algorithm (14) to construct sets for graph G from fig. 1.
Following example shows that sets CFDiSM and CFDeSM are not identically:
CFDiSM1,2 = {CF1,2,[1,2]}; CF1,2,[1,2] = {1, 3, 6, 8}
CFDiSM2,1 = {CF2,1,[2,1]}; CF2,1,[2,1] = {2, 4, 7}
CFDeSM1,2 = {CF1,2,[1,3,6,7,4,2]}; CF1,2,[1,3,6,7,4,2] = {1}
CFDeSM1,2 = {CF2,1,[2,4,7,6,3,1]}; CF2,1,[2,4,7,6,3,1] = {2}
and graphical representation of them are in fig. 3:
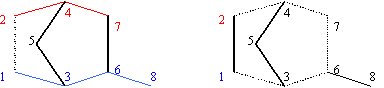
Fig. 8. CFDi1,2,[1,2] and CFDi1,2,[1,2,6,7,4,2] fragments of graph G from fig. 1
The following example shows that CFDe sets are not included in CFDi sets:
CFDiSM4,8 = {CF4,8,[4,7,6,8]}; CF4,8,[4,7,6,8] = {1, 2, 3, 4, 5};
CFDeSM4,8 = {CF4,8,[4,2,1,3,6,8]}; CF4,8,[4,2,1,3,6,8] = {4, 5, 7};
CFDiSM8,4 = {CF8,4,[8,6,7,4]} = {{8}} = {CF8,4,[8,6,3,1,2,4]} = CFDeSM8,4
and fragments are depicted in fig. 9:

Fig. 9. CFDi4,8,[4,7,6,8] and CFDe4,8,[4,2,1,3,6,8] fragments of graph G from fig. 1
The following example shows that sets CFDiSM can contain more than one fragment:
CFDiSM7,1 = {CF7,1,[7,4,2,1] , CF7,1,[7,6,3,1]};
CF7,1,[7,4,2,1] = {6, 7, 8}; CF7,1,[7,6,3,1] = {4, 5, 7}
and graphical representation of them are in fig. 10:
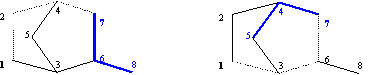
Fig. 10. CFDi7,1,[7,4,2,1] and CFDi7,1,[7,6,3,1] fragments of graph G from fig. 1
The Szeged (SzDi) fragments are defined by:
|
SzDii,j = {k : k Î V} is named SzDi fragment of i vs. j if: d(G)k,i < d(G)k,j |
(16) |
The SzDi sets are connected subgraphs (fragments). Looking at (5) and (16) definitions, is easy to observe that:
|
CJDi Í SzDi, |
(17) |
and also:
|
CFDi Ë SzDi, |
(18) |
The following construction collects the fragments SzDi for all i and j pairs of vertices:
|
For (i = 1; i < |X|; i++) For (j = i + 1; j ≤ |X|; j++) SzDii,j := Æ; SzDij,i := Æ; For (v = 1; v ≤ |X|; v++) dvi = maxint; dvj = maxint; For (ct Î T(G)v) For (k = 1; k ≤ ct[0]; k++) If (ct[k] == i) and (dvi > k) then dvi = k; EndIf; If (ct[k] == j) and (dvj > k) then dvj = k; EndIf; EndFor; EndFor; If dvi > dvj then SzDii,j È= {v}; EndIf; If dvi > dvj then SzDij,i È= {v}; EndIf; EndFor; EndFor; EndFor; |
(19) |
A graphical example of SzDi fragments for vertices 2 and 6 and graph G from fig. 1 is depicted in fig. 11:
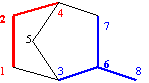
Fig. 11. SzDi2,6 and SzDi6,2 fragments of graph G from fig. 1
Like CJ and CF, SzDe sets can be defined as:
|
SzDii,j = {k : k Î V} is named SzDe set of i vs. j if: δ(G)k,i < δ(G)k,j |
(20) |
SzDe sets are not fragments (connected subgraphs). An example is depicted in fig. 12:
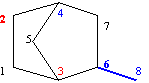
Fig. 12. SzDe2,6 = {2,3} and SzDe6,2 = {4, 6, 8} sets for graph G from fig. 1
4. A Comparison between Graph Partitioning Methods
Let us to consider the graph from fig. 13. If CFDi, CJDi and SzDi partitioning methods are applied for graph G from fig. 13 and (1,4) pair of vertices, we have:
CFDi1,4,[1,2,3,4] = {1, 8, 9, 10}; CFDi4,1,[4,3,2,1] = {4, 5, 6, 7};
CJDi1,4,[1,2,3,4] = {1, 9, 10}; CJDi4,1,[4,3,2,1] = {4, 5, 6, 7, 8};
SzDi1,4 = {1, 2, 9, 10}, SzDi4,1 = {3, 4, 5, 6, 7, 8}.
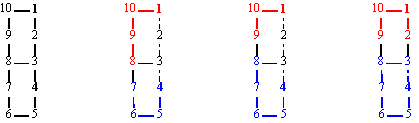
Fig. 13. Graph G = (V, E); V = {1, …, 10}; E = {(i, i+1) : 1 ≤ i ≤ 10} È {(10, 1), (8, 3)} and
CFDi1,4,[1,2,3,4], CFDi4,1,[4,3,2,1], CJDi1,4,[1,2,3,4], CJDi4,1,[4,3,2,1], SzDi1,4, SzDi4,1 sets
From fig. 13, some conclusions are immediate:
· The sets CFDi and CJDi are distinct: CF4,1,[4,3,2,1] Ì CJ4,1,[4,3,2,1] and CF1,4,[1,2,3,4] Ì CJ1,4,[1,2,3,4];
· The sets SzDi and CJDi are distinct: CJ4,1,[4,3,2,1] Ì Sz4,1 and CJ1,4,[1,2,3,4] Ì Sz1,4;
· The sets SzDi and CFDi are distinct: CF4,1,[4,3,2,1] Ì Sz4,1 and CF1,4,[1,2,3,4] Ë Sz1,4;
· The sets CFDi are not contained in sets SzDi: CF4,1,[4,3,2,1] Ì Sz4,1 and CF1,4,[1,2,3,4] Ë Sz1,4;
· The CJDi sets are contained in SzDi sets: CJ4,1,[4,3,2,1] Ì Sz4,1 and CJ1,4,[1,2,3,4] Ì Sz1,4;
Let us consider another two fragmentation methods, the minimal set that contain i vertex and not contain j vertex MIi,j:
|
MIi,j = {i} |
(21) |
and maximal set that contain i vertex and not contain j vertex:
|
MAi,j = G\{j} |
(22) |
Some interesting properties are also available now:
· MIi,j is a set that is contained in all sets generated for (i,j) pair of vertices:
|
MIi,j Í CJi,j,p; MIi,j Í CFi,j,p; MIi,j Í Szi,j |
(23) |
· MAi,j it contain all fragments generated for (i,j) pair of vertices:
|
CJi,j,p Ê MAi,j; CFi,j,p Ê MAi,j; Szi,j Ê MAi,j |
(24) |
The inclusions and intersections of sets are depicted in fig. 14:
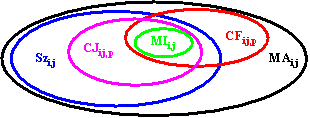
Fig. 14. Inclusions between MI, CJ, CF, SZ and MA sets
5. Graph Edges Coloring
The edges of a graph can be colored depending on which fragment are included. To apply the coloring process, is necessary to decompose the graph into connected fragments. From presented methods, connected subgraphs are obtained for CFDi, CFDe and SzDi criteria.
The CFDi criterion partition a graph G for a pair of vertices (i, j) into four regions:
· region of i’s belonging versus j, that is CFDii,j,p;
· region of j’s belonging versus i, that is CFDij,i,p;
· the path p\{i, j};
· indifferent region G\{p\{i, j} È CFDii,j,p È CFDij,i,p}
An important observation is that first three regions are connected sets of vertices (fragments) and last one (indifferent region) it can be a disconnected subgraph.
In fig. 15 are depicted partitioning of graph G from fig. 1 into four regions:
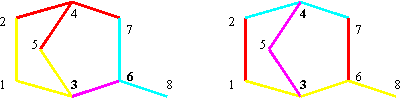
Fig. 15. Graph G from fig. 1 edges coloring in two cases: (3, 6) and (3,4) pairs of vertices
yellow: CFDii,j; turquoise: CFDij,i; pink: p\{i, j}; red: rest;
The fragments from fig. 15 are:
CFDi3,6,[3,6] = [1,2,3,5]; CFDi6,3,[6,3] = [6,7,8];
CFDi3,4,[3,5,4] = [1,3,6,8]; CFDi4,3,[4,5,3] = [2,4,7];
Note that for (3,4) pair of vertices, the remaining zone of graph, {(1, 2, 6, 7), (1, 2), (6, 7)} are not connected one.
With a similar deduction, The CFDe criterion partition a graph G for a pair of vertices (i, j) into four regions:
· region of i’s belonging versus j, that is CFDei,j,p;
· region of j’s belonging versus i, that is CFDej,i,p;
· the path p\{i, j};
· indifferent region G\{p\{i, j} È CFDei,j,p È CFDej,i,p}
An important observation is that first three regions are connected sets of vertices (fragments) and last one (indifferent region) it can be a disconnected subgraph.
In fig. 16 are depicted partitioning of graph G from fig. 1 into four regions:

Fig. 16. Graph G from fig. 1 edges coloring in two cases: (3, 6) and (3,4) pairs of vertices
yellow: CFDei,j; turquoise: CFDej,i; pink: p\{i, j}; red: rest;
The fragments from fig. 16 are:
CFDi3,6,[3,1,2,4,7,6] = [3,5]; CFDi6,3,[6,7,4,2,1,3] = [6,8];
CFDi3,4,[3,1,2,4] = [3,6,8]; CFDi4,3,[4,2,1,3] = [4,7];
Note that for (3,4) pair of vertices, the remaining zone of graph, {(1, 2, 6, 7), (1, 2), (6, 7)} are not connected one.
With a similar deduction, The SzDi criterion partition a graph G for a pair of vertices (i, j) into three regions:
· region of i’s belonging versus j, that is CFDei,j,p;
· region of j’s belonging versus i, that is CFDej,i,p;
· the equidistant region {k : d(k,i) = d(k,j)}.
An important observation is that first two regions are connected sets of vertices (fragments) and last one (equidistant region) it can be a disconnected subgraph.
In fig. 17 are depicted partitioning of graph G from fig. 1 into three regions:
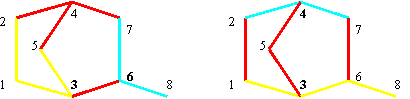
Fig. 17. Graph G from fig. 1 edges coloring in two cases: (3, 6) and (3,4) pairs of vertices
yellow: CFDei,j; turquoise: CFDej,i; red: equidistant region {k : d(k,i) = d(k,j)};
The fragments from fig. 17 are:
SzDi3,6 = [1,2,3,5]; SzDi6,3 = [6,7,8];
SzDi3,4 = [1,3,6,8]; SzDi4,3 = [2,4,7];
6. Theoretical Results (Theorems)
Theorem 1. CF is a fragment.
" i, j Î V, p Î P(G)i,j path in G from i to j then Fi,j,p fragment
Demonstration:

Fig. 18. Auxiliary construction for theorem 1 demonstration
Let v Î CFi,j,p. Then:
(Case 1) d(Gp)v,i < ¥, d(Gp)v,j = ¥ and respectively
(Case2) d(Gp)v,i < ¥, d(Gp)v,j < ¥, d(Gp)v,i < d(Gp)v,j
(Case 1, demonstration):
d(Gp)v,i < ¥ Þ $pv,i Î P(Gp)v,i (P(Gp)k,i ¹ Æ). Let k Î pv,i Þ $pk,i Î P(Gp)k,i (pk,i Í pv,i) Þ
|
d(Gp)k,i < ¥ Þ $pv,kÎ P(Gp)v,k (pv,k Í pv,i) |
(25) |
If d(Gp)k,j < ¥ Þ $pk,j Î P(Gp)k,j (P(Gp)k,j ¹ Æ). Let wv,j = pv,k È pk,j; wv,j Î W(Gp)v,j (W(Gp)v,j ¹ Æ) Þ d(Gp)v,j £ l(pv,k) + l(pk,j) < ¥ contradiction with d(Gp)v,j = ¥ Þ
|
d(Gp)k,j = ¥ |
(26) |
From (25) and (26) Þ k Î CFi,j,p Þ pv,i Í CFi,j,p Þ v connected with i in CFi,j,p Þ
|
CFi,j,p connected |
(27) |
(Case 2, demonstration):
d(Gp)v,i < ¥ Þ $pv,i Î P(Gp)v,i s. th. l(pv,i) = min{l(q), q Î P(Gp)v,i} (P(Gp)v,i ¹ Æ; l(pv,i) = d(Gp)v,i). Let k Î pv,i Þ
|
$ pk,i Î P(Gp)k,i (pk,i Í pv,i) , $pv,k Î P(Gp)v,k (pv,k Í pv,i) |
(28) |
Because a geodesic path can contain only geodesic paths, from (28) it results:
l(pk,i) = d(Gp)k,i , l(pv,k) = d(Gp)v,k , l(pv,i) = l(pv,k) + l(pk,i) Þ d(Gp)v,i = d(Gp)v,k + d(Gp)k,i
d(Gp)v,j £ d(Gp)v,k + d(Gp)k,j (d(Gp) a metric); (28) Þ d(Gp)v,j -d(Gp)v,i £ d(Gp)k,j - d(Gp)k,i
From d(Gp)v,i < d(Gp)v,j Þ 0 <d(Gp)v,j - d(Gp)v,i£d(Gp)k,j-d(Gp)k,i and then:
d(Gp)k,i < d(Gp)k,j Þ k Î CFi,j,p Þ pv,i Í CFi,j,p Þ
|
v connected with i in CFi,j,p Þ CFi,j,p connected |
(29) |
From (27) and (29) it result that CFi,j,p is a connected subgraph (q.e.d.).
Theorem 2. SzDi is a fragment.
"i, j Î V then SZDii,j fragment
Demonstration:
Let v Î SZDii,j. Then d(G)v,i < ¥, d(G)v,j < ¥, d(G)v,i < d(G)v,j (G connected graph).
From d(G)v,i < ¥ Þ $pv,i Î P(G)v,i s. th. l(pv,i) = min{l(q), qÎ P(G)v,i} (P(G)v,i ¹ Æ; l(pv,i) = d(G)v,i). Let k Î pv,i Þ
|
$ pk,i Î P(G)k,i (pk,i Í pv,i) , $pv,k Î P(G)v,k (pv,k Í pv,i) |
(30) |
Because a geodesic path can contain only geodesic paths, from (28) it results:
l(pk,i) = d(G)k,i , l(pv,k) = d(G)v,k , l(pv,i) = l(pv,k) + l(pk,i) Þ d(G)v,i = d(G)v,k + d(G)k,i
d(G)v,j £ d(G)v,k + d(G)k,j (d(G) a metric); (30) Þ d(G)v,j - d(G)v,i £ d(G)k,j - d(G)k,i
Because d(G)v,i < d(G)v,j Þ 0 < d(G)v,j-d(G)v,i £ d(G)k,j-d(G)k,i and then
d(G)k,i < d(G)k,j Þ k Î SzDii,j Þ pv,i Í SzDii,j Þ v connected with i in SzDii,j Þ
SzDii,j connected subgraph (q.e.d.).
Theorem 3. CJDi sets are contained in SzDi fragments.
CJDii,j,p Ì SzDii,j
Demonstration:
Let v Î CJDii,j,p. According to definition of CJDi set,
|
d(G)v,i < d(G)v,j |
(31) |
This is (according to the definition of SzDi fragment) a necessary and enough such that v Î SzDii,j,p. From here, it result immediately that CJDii,j,p Ì SzDii,j (q.e.d.).
References