Graph Theory.

2. Vertex Descriptors and Graph Coloring

Lorentz JÄNTSCHI

Technical University of Cluj-Napoca

http://lori.academicdirect.ro

Abstract

This original work presents the construction of a set of ten sequence matrices and their applications for ordering vertices in graphs. For every sequence matrix three ordering criteria are applied: lexicographic ordering, based on strings of numbers, corresponding to every vertex, extracted as rows from sequence matrices; ordering by the sum of path lengths from a given vertex; and ordering by the sum of paths, starting from a given vertex.

We also examine a graph that has different orderings for the above criteria. We then proceed to demonstrate that every criterion induced its own partition of graph vertex.

We propose the following theoretical result: both LAVS and LVDS criteria generate identical partitioning of vertices in any graph.

Finally, a coloring of graph vertices according to introduced ordering criteria was proposed.

Keywords

Graph theory, Vertex descriptors, Matrix based descriptors, Invariants, Graph coloring, Graph partitioning.

1. Introduction

The problem of vertex partitioning in graphs can be solved in different ways [1],[2]. The most frequently used discriminating criteria are well-known square matrices that collect contributions of pairs of vertices from the graph. The adjacency matrix is the simplest matrix of this type. Some authors use characteristic polynomial and its eigenvalue to characterize a given graph [3]. The sequence of eigenvalues forms the graph spectrum [4]. A basic result in spectral geometry is the theorem of Cheng [5].

            Let us consider a sequence matrix. It is of dimension n×(n-1), where n is the number of vertices. Such a matrix can be used to compare different graphs (interstructural similarity), when analyzing the columns of sequence matrices, the sums by columns or global sums (generic indices) [6]. It is also possible to compare the vertices of a graph (intrastructural similarity), when analyzing the rows of sequence matrices and the sums by rows [7],[8]. With this observation, a sequence matrix is an elegant method to investigate graphs [9]. Note that the ordering of graph vertices by using sequence matrices is of a partially ordered type [10],[11].

Prior, Dobrynin reported the degeneracy of some sequence matrices [12],[13]. Decomposition of graphs into congruent factors has interesting chemical implications [14],[15]. Dobrynin [16] and Diudea [17],[18] reported distance degree sequences (DPS in our notation) and their chemical applications. The path sequence matrix (APS in our notation) is calculated in order to study molecular similarity [19].

2. Theoretical Considerations

Some definitions are required. Let G = (V, E) be an un-oriented graph. We are note the set of all path in G with P(G). The distance from i to j in G is d(G)_i,j and detour is δ(G)_i,j. For p Î P(G), l(p) denotes the length of path p.

t = (v_i)_1≤i≤n is a terminal path if:

(1) t Î P(G) and

(2) "v Î V s. th. (v_n, v) Î E then t È (v_n, v) Ï P(G).

The set of terminal paths starting with i in G is T(G)_i = {t = (v_i)_1≤i≤n s. th. v₁ = i and t terminal path}. The set of terminal paths in G is T(G) = (T(G)_v)_vÎV.

The set of distance paths from i to j in G is DP(G)_i,j = {p=(x_i)_1£i£n s. th. pÎP(G), x₁=i, x_n=j & l(p)=d(G)_i,j}. The set of distance path in G is DP(G) = {p = (x_i)_1£i£n s. th. p Î P(G) and l(p) = }.

The set of detour paths from i to j in G is ΔP(G)_i,j = {p=(x_i)_1£i£n s. th. pÎP(G), x₁=i, x_n=j & l(p)=δ(G)_i,j}. The set of detour path in G is ΔP(G) = {p = (x_i)_1£i£n s. th. p Î P(G) and l(p) = }.

The set of distance terminal paths from i to j in G is DT(G)_i,j = {t=(x_i)_1£i£n s. th. tÎT(G), x₁=i, x_n=j & l(t)=d(G)_i,j}.

The set of distance terminal path in G is DT(G) = {t = (x_i)_1£i£n s. th. t Î T(G) and l(t) = }.

The set of detour terminal paths from i to j in G is ΔT(G)_i,j = {t=(x_i)_1£i£n s. th. tÎT(G), x₁=i, x_n=j & l(t)= δ(G)_i,j}.

The set of detour terminal path in G is ΔT(G) = {t = (x_i)_1£i£n s. th. t Î T(G) and l(t) = }.

            Note that if G = (V, E) is a connected graph, then " v Î V, " e Î E $ t Î T(G)_v s. th. e Í t. Thus, any connected graph can be reconstructed from the terminal path list starting from an arbitrary vertex. Also, " i, j Î V, T(G)_j can be constructed from T(G)_i. Consequently, the sets of terminal paths T(G)_v, v Î V are equivalent by construction.

            In order to generate sequence matrices, we compute terminal paths. Let G = (V, E), V = {1, …, 8}, E = {(1, 2), (1, 3), (2, 4), (3, 5), (3, 6), (4, 5), (4, 7), (6, 7), (7,8)} shown in figure 1:

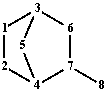
Fig. 1. Graph G (see above)

            We have devised a 16-bit windows original computer program to list all terminal paths. For the graph in figure 1, we have obtained the following set of terminal paths for vertex 1:

T(G)₁

                                    1          2          4          5          3          6          7          8

                                    1          2          4          7          8

                                    1          2          4          7          6          3          5

                                    1          3          6          7          8

                                    1          3          6          7          4          2

                                    1          3          6          7          4          5

                                    1          3          5          4          7          6

                                    1          3          5          4          7          8

                                    1          3          5          4          2

Fig. 2. Terminal paths of graph G from fig. 1 starting from vertex 1

3. The Construction of Sequence Matrices of Numbering

We extend the concept used for the distance degree sequence matrix¹⁶ and layer path (path degree sequence)¹⁹ matrix to construct a set of 10 sequence matrices. A sequence matrix is a matrix that collects vertex contribution in each row and elongation of paths in each column. The elements of the matrix cumulate a value of vertex property for a given elongation. Sequence matrices are of dimension n×(n-1) and are given by following definitions:

SMN (sequence matrix of numbering) of paths (P) which starts with i and has length j is APS(G)_i,j = |{p Î P(G), s. th. p₁ = i, l(p) = j}|, where p₁ is the first vertex from path p and operator |∙| is the cardinal operator.

SMN of distance P that starts with i and has length j is DPS(G)_i,j = |{p Î APS(G)_i,j, s. th. p Î DP(G)}|.

SMN of detour P that starts with i and has length j is ΔPS(G)_i,j = |{p Î APS(G)_i,j, s. th. p Î ΔP(G)}|.

SMN of terminal paths (T) which starts with i and has length j is ATS(G)_i,j = |{t Î T(G), s. th. t₁ = i, l(t) = j}}|.

SMN of distance T that starts with i and has length j is DTS(G)_i,j = |{p Î ATS(G)_i,j, s. th. p Î DT(G)}|.

SMN of detour T that starts with i and has length j is ΔTS(G)_i,j = |{p Î ATS(G)_i,j, s. th. p Î ΔT(G)}|.

SMN of the vertex situated at the end of paths that starts with i and has j edges is AVS(G)_i,j = |{vÎV, s. th. $ p Î P(G), p₁ = i, p_j+1 = v, l(p) = j}|.

SMN of the vertex situated at the end of distance paths that starts with i and has j edges is DVS(G)_i,j = |{vÎV, s. th. $ pÎDP(G), p₁ = i, p_j+1 = v, l(p)=j}|.

SMN of the vertex situated at the end of detour paths that starts with i and has j edges is ΔVS(G)_i,j = |{vÎV, s. th. $ pÎΔP(G), p₁ = i, p_j+1 = v, l(p)=j}|.

SMN of the cycles that contain vertex i and has j edges is ACS(G)_i,j = |{p Î P(G), s. th. l(p) = j-1 and (p_j,p₁) Î E}|.

            If an lexicographically ordering are applied to the sequence matrices of numbering (SMN), through permutation of one line with another, and the new matrix obtained can be used to make interstructural comparisons (with any other graph) because a lexicographically ordered matrix is independent with respect to labeling.

When two vertices are compared, lexicographic ordering is also useful from the point of view of the selected criterion.

The results of lexicographic ordering can be used to index the graph, by permuting the old indexing.

The computer program used in lexicographic ordering (quicksort method), gives permutation of partial ordering (σ in what follows).

            Ten sequence matrices, ten lexicographically associated matrices and ten permutations σ are computed.

Two vertex indices in every case (from ten cases) are calculated. The first is sum of elements from the row (the number of total paths), the second is the weighted sum of elements from the row (the length of total paths).

For the graph G from figure 1 we obtain a set of ten tables with three different ordering criteria (table 1-10).

Table 1. APS and LAPS numbered sequences

APS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i	LAPS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i
1	2	3	4	7	6	2	1	25	97	1=σ(8)	1	2	3	4	5	5	2	22	99
2	2	3	5	5	6	4	0	25	97	2=σ(1)	2	3	4	7	6	2	1	25	97
3	3	3	5	7	3	0	0	21	67	3=σ(2)	2	3	5	5	6	4	0	25	97
4	3	4	4	6	3	1	0	21	68	4=σ(6)	2	4	4	5	6	3	0	24	90
5	2	4	5	5	4	5	1	26	102	5=σ(5)	2	4	5	5	4	5	1	26	102
6	2	4	4	5	6	3	0	24	90	6=σ(7)	3	3	4	5	5	2	0	22	78
7	3	3	4	5	5	2	0	22	78	7=σ(3)	3	3	5	7	3	0	0	21	67
8	1	2	3	4	5	5	2	22	99	8=σ(4)	3	4	4	6	3	1	0	21	68

Table 2. DPS and LDPS numbered sequences

DPS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i	LDPS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i
1	2	3	2	2	0	0	0	9	22	1=σ(8)	1	2	3	2	0	0	0	8	22
2	2	3	3	0	0	0	0	8	17	2=σ(1)	2	3	2	2	0	0	0	9	22
3	3	3	1	0	0	0	0	7	12	3=σ(2)	2	3	3	0	0	0	0	8	17
4	3	4	0	0	0	0	0	7	11	4=σ(5)	2	4	1	0	0	0	0	7	13
5	2	4	1	0	0	0	0	7	13	5=σ(6)	2	4	2	0	0	0	0	8	16
6	2	4	2	0	0	0	0	8	16	6=σ(3)	3	3	1	0	0	0	0	7	12
7	3	3	2	0	0	0	0	8	15	7=σ(7)	3	3	2	0	0	0	0	8	15
8	1	2	3	2	0	0	0	8	22	8=σ(4)	3	4	0	0	0	0	0	7	11

Table 3. ΔPS and LΔPS numbered sequences

ΔPS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i	LΔPS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i
1	0	0	0	1	4	2	1	8	43	1=σ(1)	0	0	0	1	4	2	1	8	43
2	0	0	0	1	4	4	0	9	48	2=σ(6)	0	0	0	1	4	3	0	8	42
3	0	0	2	4	3	0	0	9	37	3=σ(2)	0	0	0	1	4	4	0	9	48
4	0	0	2	4	2	1	0	9	38	4=σ(5)	0	0	0	4	0	4	1	9	47
5	0	0	0	4	0	4	1	9	47	5=σ(4)	0	0	2	4	2	1	0	9	38
6	0	0	0	1	4	3	0	8	42	6=σ(3)	0	0	2	4	3	0	0	9	37
7	1	0	0	1	4	2	0	8	37	7=σ(8)	1	0	0	0	1	4	2	8	44
8	1	0	0	0	1	4	2	8	44	8=σ(7)	1	0	0	1	4	2	0	8	37

Table 4. ATS and LATS numbered sequences

ATS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i	LATS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i
1	0	0	0	3	4	1	1	9	45	1=σ(8)	0	0	0	0	1	3	2	6	37
2	0	0	1	1	3	4	0	9	46	2=σ(1)	0	0	0	3	4	1	1	9	45
3	0	0	1	5	3	0	0	9	38	3=σ(5)	0	0	1	1	0	4	1	7	38
4	0	1	0	3	2	1	0	7	30	4=σ(2)	0	0	1	1	3	4	0	9	46
5	0	0	1	1	0	4	1	7	38	5=σ(3)	0	0	1	5	3	0	0	9	38
6	0	1	0	0	3	3	0	7	35	6=σ(6)	0	1	0	0	3	3	0	7	35
7	1	0	0	1	3	2	0	7	32	7=σ(4)	0	1	0	3	2	1	0	7	30
8	0	0	0	0	1	3	2	6	37	8=σ(7)	1	0	0	1	3	2	0	7	32

Table 5. DTS and LDTS numbered sequences

DTS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i	LDTS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i
1	0	0	0	2	0	0	0	2	8	1=σ(8)	0	0	0	0	0	0	0	0	0
2	0	0	1	0	0	0	0	1	3	2=σ(1)	0	0	0	2	0	0	0	2	8
3	0	0	1	0	0	0	0	1	3	3=σ(3)	0	0	1	0	0	0	0	1	3
4	0	1	0	0	0	0	0	1	2	4=σ(5)	0	0	1	0	0	0	0	1	3
5	0	0	1	0	0	0	0	1	3	5=σ(2)	0	0	1	0	0	0	0	1	3
6	0	1	0	0	0	0	0	1	2	6=σ(4)	0	1	0	0	0	0	0	1	2
7	1	0	0	0	0	0	0	1	1	7=σ(6)	0	1	0	0	0	0	0	1	2
8	0	0	0	0	0	0	0	0	0	8=σ(7)	1	0	0	0	0	0	0	1	1

Table 6. ΔTS and LΔTS numbered sequences

ΔTS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i	LΔTS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i
1	0	0	0	0	2	1	1	4	23	1=σ(8)	0	0	0	0	0	2	2	4	26
2	0	0	0	0	1	4	0	5	29	2=σ(5)	0	0	0	0	0	3	1	4	25
3	0	0	0	2	3	0	0	5	23	3=σ(6)	0	0	0	0	1	3	0	4	23
4	0	0	0	2	1	1	0	4	19	4=σ(2)	0	0	0	0	1	4	0	5	29
5	0	0	0	0	0	3	1	4	25	5=σ(1)	0	0	0	0	2	1	1	4	23
6	0	0	0	0	1	3	0	4	23	6=σ(4)	0	0	0	2	1	1	0	4	19
7	1	0	0	0	2	2	0	5	23	7=σ(3)	0	0	0	2	3	0	0	5	23
8	0	0	0	0	0	2	2	4	26	8=σ(7)	1	0	0	0	2	2	0	5	23

Table 7. AVS and LAVS numbered sequences

AVS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i	LAVS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i
1	3	6	7	8	8	8	8	48	212	1=σ(8)	2	4	7	8	8	8	8	45	207
2	3	6	8	8	8	8	8	49	215	2=σ(1)	3	6	7	8	8	8	8	48	212
3	4	7	8	8	8	8	8	51	218	3=σ(2)	3	6	8	8	8	8	8	49	215
4	4	8	8	8	8	8	8	52	220	4=σ(5)	3	7	8	8	8	8	8	50	217
5	3	7	8	8	8	8	8	50	217	5=σ(6)	3	7	8	8	8	8	8	50	217
6	3	7	8	8	8	8	8	50	217	6=σ(3)	4	7	8	8	8	8	8	51	218
7	4	7	8	8	8	8	8	51	218	7=σ(7)	4	7	8	8	8	8	8	51	218
8	2	4	7	8	8	8	8	45	207	8=σ(4)	4	8	8	8	8	8	8	52	220

Table 8. DVS and LDVS numbered sequences

DVS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i	LDVS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i
1	2	3	1	1	0	0	0	7	15	1=σ(8)	1	2	3	1	0	0	0	7	18
2	2	3	2	0	0	0	0	7	14	2=σ(1)	2	3	1	1	0	0	0	7	15
3	3	3	1	0	0	0	0	7	12	3=σ(2)	2	3	2	0	0	0	0	7	14
4	3	4	0	0	0	0	0	7	11	4=σ(5)	2	4	1	0	0	0	0	7	13
5	2	4	1	0	0	0	0	7	13	5=σ(6)	2	4	1	0	0	0	0	7	13
6	2	4	1	0	0	0	0	7	13	6=σ(3)	3	3	1	0	0	0	0	7	12
7	3	3	1	0	0	0	0	7	12	7=σ(7)	3	3	1	0	0	0	0	7	12
8	1	2	3	1	0	0	0	7	18	8=σ(4)	3	4	0	0	0	0	0	7	11

Table 9. ΔVS and LΔVS numbered sequences

ΔVS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i	LΔVS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i
1	0	0	0	1	3	2	1	7	38	1=σ(1)	0	0	0	1	3	2	1	7	38
2	0	0	0	1	3	3	0	7	37	2=σ(2)	0	0	0	1	3	3	0	7	37
3	0	0	1	3	3	0	0	7	30	3=σ(6)	0	0	0	1	3	3	0	7	37
4	0	0	1	3	2	1	0	7	31	4=σ(5)	0	0	0	2	0	4	1	7	39
5	0	0	0	2	0	4	1	7	39	5=σ(4)	0	0	1	3	2	1	0	7	31
6	0	0	0	1	3	3	0	7	37	6=σ(3)	0	0	1	3	3	0	0	7	30
7	1	0	0	1	3	2	0	7	32	7=σ(8)	1	0	0	0	1	3	2	7	38
8	1	0	0	0	1	3	2	7	38	8=σ(7)	1	0	0	1	3	2	0	7	32

Table 10. ACS and LACS numbered sequences

ACS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i	LACS	1	2	3	4	5	6	7	ΣiSi,j	ΣiSi,j∙i
1	0	0	0	1	1	0	0	2	11	1=σ(8)	0	0	0	0	0	0	0	0	0
2	0	0	0	1	1	0	0	2	11	2=σ(1)	0	0	0	0	1	1	0	2	11
3	0	0	0	2	1	0	0	3	16	3=σ(2)	0	0	0	0	1	1	0	2	11
4	0	0	0	2	1	0	0	3	16	4=σ(6)	0	0	0	0	1	1	0	2	11
5	0	0	0	2	0	0	0	2	10	5=σ(7)	0	0	0	0	1	1	0	2	11
6	0	0	0	1	1	0	0	2	11	6=σ(5)	0	0	0	0	2	0	0	2	10
7	0	0	0	1	1	0	0	2	11	7=σ(3)	0	0	0	0	2	1	0	3	16
8	0	0	0	0	0	0	0	0	0	8=σ(4)	0	0	0	0	2	1	0	3	16

4. Graph Partitioning

Three operators on SMN matrices were applied for vertex comparison: LSMN (lexicographically ordered matrix of numbering), SMNΣ_pn_p (sum of all path number that satisfy selected criteria) and SMNΣ_pn_p∙l(p) (sum of all length of path that satisfy selected criteria).

Every operator induces a partial ordering in V (the set of vertices form the graph), and partitions the vertices in classes of equivalence that it correspond to equal operator values.

            For example, 1 is equivalent with 2 by APSΣ_pn_p, with 6,7 and 8 by ΔPSΣ_pn_p, with 2, 6, 7 by ACS and ACSΣ_pn_p∙l(p), with 2, 5, 6, 7 by ACSΣ_pn_p, with 4, 5, 6 and 8 by ΔTSΣ_pn_p. All vertices are equivalent by ΔVSΣ_pn_p and DVSΣ_pn_p. Vertex 1 is singulary according to APSΣ_pn_p∙l(p), DPSΣ_pn_p, ΔPSΣ_pn_p∙l(p), ATSΣ_pn_p∙l(p), LDTS, DTSΣ_pn_p, DTSΣ_pn_p∙l(p), LAVS, AVSΣ_pn_p, AVSΣ_pn_p∙l(p), LDVS, DVSΣ_pn_p∙l(p) and LΔVS.

            This example demonstrates the flexibility of sequence matrix criteria in the characterization of various properties of vertices.

            Let us look at all partial orderings induced in the graph by every sequence matrix.

            LAPS discriminates all vertices for the graph in fig. 1. The values obtained by applying Σ_pn_p and Σ_pn_p∙l(p) operators are degenerate in the case of APS. APSΣ_pn_p partitioning V(G) in 5 classes of equivalence:

P(V(G), APSΣ_pn_p) = {(3,4), (7,8), (6), (1,2), (5)}.

APSΣ_pn_p∙l(p) partitions V(G) in 7 classes of equivalence:

P(V(G), APSΣ_pn_p∙l(p)) = {(7), (8), (6), (4), (2,3), (1), (5)}.

            LDPS discriminates all vertices for the graph in fig. 1. The values for Σ_pn_p and Σ_pn_p∙l(p) operators are degenerate in the case of DPS.

DPSΣ_pn_p partitions V(G) in 3 classes of equivalence:

P(V(G), DPSΣ_pn_p) = {(3,4,5), (2,6,7,8), (1)}.

DPSΣ_pn_p∙l(p) partitions V(G) in 7 classes of equivalence:

P(V(G), DPSΣ_pn_p∙l(p)) = {(8), (6), (4), (7), (5), (3), (1,2)}.

All vertices for the graph from fig. 1 are discriminated by LΔPS criterion. The values for Σ_pn_p and Σ_pn_p∙l(p) operators are degenerate according to ΔPS criterion.

ΔPSΣ_pn_p partitions V(G) in 2 classes of equivalence:

P(V(G), ΔPSΣ_pn_p) = {(1,6,7,8), (2,3,4,5)}.

ΔPSΣ_pn_p∙l(p) partitions V(G) in 7 classes of equivalence:

P(V(G), ΔPSΣ_pn_p∙l(p)) = {(3,7), (4), (6), (1), (8), (5), (2)}.

LATS discriminates all vertices for the graph G. The values for Σ_pn_p and Σ_pn_p∙l(p) are degenerate according to ATS.

ATSΣ_pn_p partitions V(G) in 3 classes of equivalence:

P(V(G), ATSΣ_pn_p) = {(8), (4,5,6,7), (1,2,3)}.

ATSΣ_pn_p∙l(p) partitions V(G) in 7 classes of equivalence:

P(V(G), ATSΣ_pn_p∙l(p)) = {(4), (7), (6), (8), (3,5), (1), (2)}.

LDTS partitions the vertices of G in 5 classes of equivalence:

P(V(G), LDTS) = {(8), (1), (2,3,5), (4,6), (7)}.

The values for Σ_pn_p and Σ_pn_p∙l(p) operators are degenerate according to DTS.

DTSΣ_pn_p partitions V(G) in 3 classes of equivalence:

P(V(G), DTSΣ_pn_p) = {(8), (2,3,4,5,6,7), (1)}.

DTSΣ_pn_p∙l(p) partitions V(G) in 5 classes of equivalence:

P(V(G), DTSΣ_pn_p∙l(p)) = {(8), (7), (4,6), (2,3,5), (1)}.

            LΔTS discriminates all vertices for the graph in fig. 1. The values for Σ_pn_p and Σ_pn_p∙l(p) operators are degenerate in ΔTS criteria.

ΔTSΣ_pn_p partitions V(G) in 2 classes of equivalence:

P(V(G), ΔTSΣ_pn_p) = {(1,4,5,6,8), (2,3,7)}.

ΔTSΣ_pn_p∙l(p) partitions V(G) in 5 classes of equivalence:

P(V(G), ΔTSΣ_pn_p∙l(p)) = {(4), (1,3,6,7), (5), (8), (2)}.

LAVS partitions the vertices of G in 6 classes of equivalence:

P(V(G), LAVS) = {(8), (1), (2), (5,6), (3,7), (4)}.

The values for Σ_pn_p and Σ_pn_n∙l(p) are degenerate in AVS criteria.

AVSΣ_pn_p partitions V(G) in 6 classes of equivalence:

P(V(G), AVSΣ_pn_p) = {(8), (1), (2), (5,6), (3,7), (4)}.

AVSΣ_pn_p∙l(p) partitions V(G) in 6 classes of equivalence:

P(V(G), AVSΣ_pn_p∙l(p)) = {(8), (1), (2), (5,6), (3,7), (4)}.

LDVS partitions the vertices of G in 6 classes of equivalence:

P(V(G), LDVS) = {(8), (1), (2), (5,6), (3,7), (4)}.

The values for Σ_pn_p and Σ_pn_p∙l(p) are degenerate in DVS criteria.

DVSΣ_pn_p does not discriminate the vertices of G:

P(V(G), DVSΣ_pn_p) = {(1,2,3,4,5,6,7,8)}.

DVSΣ_pn_p∙l(p) partitions V(G) in 6 classes of equivalence:

P(V(G), DTSΣ_pn_p∙l(p)) = {(4), (3,7), (5,6), (2), (1), (8)}.

LΔVS partitions V(G) in 7 classes of equivalence:

P(V(G), LΔVS) = {(1), (2,6), (5), (4), (3), (8), (7)}.

The values for Σ_pn_p and Σ_pn_p∙l(p) operators are totally degenerate in ΔVS criteria.

ΔVSΣ_pn_p partitions does not discriminate the vertices:

P(V(G), ΔVSΣ_pn_p) = {(1,2,3,4,5,6,7,8)}.

ΔVSΣ_pn_p∙l(p) partitions V(G) in 6 classes of equivalence:

P(V(G), ΔVSΣ_pn_p∙l(p)) = {(3), (4), (7), (2,6), (1,8), (5)}.

LACS partitions V(G) in 4 classes of equivalence:

P(V(G), LACS) = {(8), (1,2,6,7), (5), (3,4)}.

The values for Σ_pn_p and Σ_pn_p∙l(p) are degenerate in ACS.

ACSΣ_pn_p partitions V(G) in 3 classes:

P(V(G), ACSΣ_pn_p) = {(8), (1,2,5,6,7), (3,4)}.

ACSΣ_pn_p∙l(p) partitions V(G) in 4 classes of equivalence:

P(V(G), ACSΣ_pn_p∙l(p)) = {(8), (5), (1,2,6,7), (3,4)}.

Note that the matrices LAVS and LDVS contain different values, but induce the same ordering "σ" for vertices:

σ_LAVS =  = σ_LDVS                                                                (σP)

The property (σP) was verified by a set of various graphs, with different numbers of cycles, edges and vertices. In each case, the LAVS and LDVS criteria induce the same partial ordering for vertices.

5. Vertices Coloring

According to the partitions induced and presented in tables 1-10 a graph vertices coloring are making. In colorings, a code color was used. In increasing order of values for selected criteria, the colors used are red, gold, blue, lavender, lime, green and brown. For the partitions that discriminate all vertices no coloring was made.

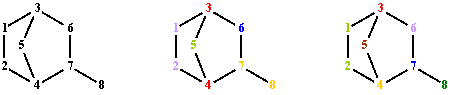
Fig. 3. Graph G vertices colorings from fig. 1; partitions: LAPS, APSΣ_pn_p and APSΣ_pn_p∙l(p)

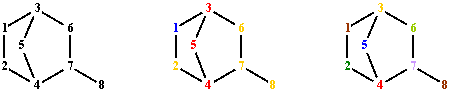
Fig. 4. Graph G vertices colorings from fig. 1; partitions: LDPS, DPSΣ_pn_p and DPSΣ_pn_p∙l(p)

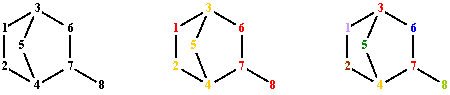
Fig. 5. Graph G vertices colorings from fig. 1; partitions: LΔPS, ΔPSΣ_pn_p and ΔPSΣ_pn_p∙l(p)

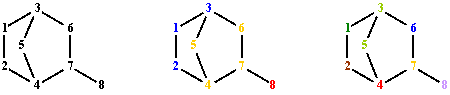
Fig. 6. Graph G vertices colorings from fig. 1; partitions: LATS, ATSΣ_pn_p and ATSΣ_pn_p∙l(p)

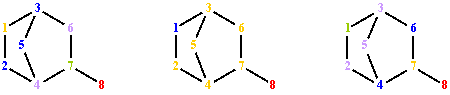
Fig. 7. Graph G vertices colorings from fig. 1; partitions: LDTS, DTSΣ_pn_p and DTSΣ_pn_p∙l(p)

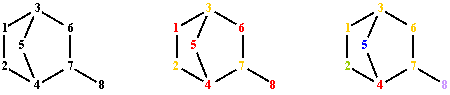
Fig. 8. Graph G vertices colorings from fig. 1; partitions: LΔTS, ΔTSΣ_pn_p and ΔTSΣ_pn_p∙l(p)

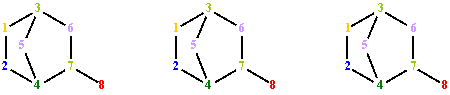
Fig. 9. Graph G vertices colorings from fig. 1; partitions: LAVS, AVSΣ_pn_p and AVSΣ_pn_p∙l(p)

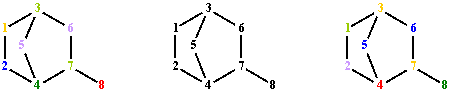
Fig. 10. Graph G vertices colorings from fig. 1; partitions: LDVS, DVSΣ_pn_p and DVSΣ_pn_p∙l(p)

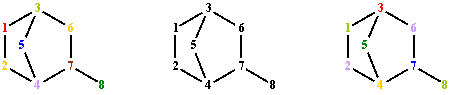
Fig. 11. Graph G vertices colorings from fig. 1; partitions: LΔVS, ΔVSΣ_pn_p and ΔVSΣ_pn_p∙l(p)

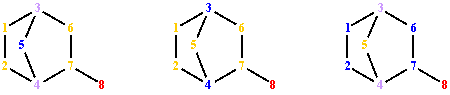
Fig. 12. Graph G vertices colorings from fig. 1; partitions: LACS, ACSΣ_pn_p and ACSΣ_pn_p∙l(p)

6. Conclusions

The analyzed matrix critters are capable to partitioning vertices in equivalence classes by different properties (i.e. number of paths, length of paths, et all).

All criteria give a specific partitioning of vertices, excepting LAVS and LDVS ordering. For LAVS and LDVS criterion, an interesting property result: although the individual matrix values are different, comparison rules match, so that the two matrices induce identical partitioning. Testing on a large set of graphs, the partitioning rule LADS ≡ LVDS remain same.

That is a subject for a new theorem that will be proved later.

More, all AVS criterion (AVSΣ_pn_p and AVSΣ_pn_p∙l(p) and LAVS) make same partitioning of graph vertices for the given graph G from fig. 1. More, the ordering is the same (see fig. 9).

Vertex partitioning can be applied in graph coloring [20], the theory of traffic (lights), distributed electric circuits, computer networks [21], and chemical graphs [22]. Edge partitioning is another problem that can be solved using terminal path structure. For more details about this subject, please consult [23].

References

---

[1]. Liu X., Balasubramanian K., Munk E. M., 'Computational Techniques for Vertex Partitioning of Graphs', J. Chem. Comput. Sci., 30 (1990), 263-269.

[2]. Skorobogatov A. V., Dobrynin A. A., 'Metric Analysis of Graphs', Commun. Math. Comput. Chem., 23 (1988), 105-151.

[3]. Quenell T., 'Eigenvalue comparisons in Graph Theory', Pacific J. of Math., 176-2 (1996), 443-461.

[4]. Harary F., Schwenk A. J., 'The Spectral Approach to Determining the Number of Walks in a Graph', Pacific J. of Math., 80-2 (1979), 443-449.

[5]. Cheng S.-Y., 'Eigenvalue Comparison Theorems and Its Geometric Applications', Math. Z., 143 (1975), 289-297.

[6]. Basak C. S., R. V. Magnusson, G. Niemi, R. Regal, 'Determining Structural Similarity of Chemicals Using Graph-Theoretic Indices', Discr. Appl. Math., 19 (1988), 17-44.

[7]. Liu X., Balasubramanian K., E. M. Munk, 'Computational Techniques for Vertex Partitioning of Graphs', J. Chem. Inf. Comput. Sci., 30 (1990), 263-269.

[8]. Bersohn M., 'A Matrix Method for Partitioning the Atoms of a Molecule Into Equivalence Classes', Comput. Chem., 11 (1987), 67-72.

[9]. Balaban A. T., 'Local versus Global (i.e. Atomic versus Molecular) Numerical Modelling of Molecular Graphs', J. Chem. Inf. Comput. Sci., 34 (1994), 398-402.

[10]. Lerman M., Soare I. R., 'd-Simple Sets, Small Sets and Degree Classes', Pacific J. of Math., 87-1 (1980), 135-155.

[11]. Dhar D., 'Asymptotic Enumeration of Partially Ordered Sets', Pacific J. of Math., 90-2 (1980), 299-306.

[12]. Dobrynin A. A., 'Degeneracy of Some Matrix Graph Invariants', J. of Math. Chem., 14 (1993) 175-184.

[13]. Dobrynin A. A., 'Cubic Graphs with 62 Vertices Having the Same Path Layer Matrix', J. Graph Theory, 17 (1993), 1-4.

[14]. Balaban A. T., 'Applications of Graph Theory in Chemistry', J. Chem. Inf. Comput. Sci., 25 (1985), 334-343.

[15]. Balaban A. T., 'Solved and Unsolved Problems in Chemical Graph Theory', Annals of Discr. Math., 55 (1993), 109-126.

[16]. Dobrynin A. A., Kochetova A. A., 'Degree Distance of a Graph: A Degree Analogue of the Wiener Index', J. Chem. Inf. Comput. Sci., 36 (1996), 1082-1086.

[17]. Diudea M. V., 'Layer Matrices in Molecular Graphs', J. Chem. Inf. Comput. Sci., 34 (1994), 1064-1071.

[18]. Diudea M. V., Topan M., Graovac A., 'Layer Matrices of Walk Degrees', J. Chem. Inf. Comput. Sci., 34 (1994), 1072-1078.

[19]. Randić M., 'Design of Molecules with Desired Properties (A Molecular Similarity Approach to Property Optimization),' in 'Concept and Applications of Molecular Similarity', Ed. A. M. Johnson, G. M. Maggiora, John Wiley & Sons, 5 (1990), 77-145.

[20]. Exoo G., 'Some New Ramsey Colorings', The Electronic J. of Combinatorics, 5 (1998), #R29(1-5).

[21]. Jäntschi L., L. M. Ungureşan, 'Special Chapters of Chemistry for Automatics' (in Romanian), U. T. Pres, Cluj-Napoca, Romania, (2001), 1-202.

[22]. Diudea M. V., Gutman I., Jäntschi L., 'Molecular Topology', Nova Science, Huntington, New York, (2001), 1-332.

[23]. Jäntschi L., 'Graph Theory. 1. Fragmentation of Structural Graphs', Leonardo Electronic Journal of Practices and Technologies, 1 (2002), 19-36.