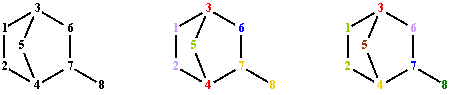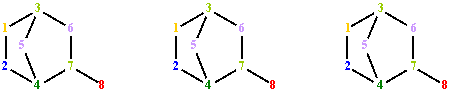
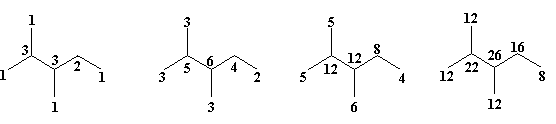
 SVTI (s-Bu) = 1+ 2 + 2 + 3 = 8
SVTI (s-Bu) = 1+ 2 + 2 + 3 = 8

| ||||
| G1 | G1(1,5) | G1(2) | G1(3) | G1(4) |
G2 |
|
| ||||
| G2 {1Wi } | G2 {2Wi } | G2 {3Wi} | G2 {4Wi } | |
| L1W | L2W | L3W | L4W | |
| i\j | 0 1 2 3 4 | 0 1 2 3 4 | 0 1 2 3 4 | 0 1 2 3 4 |
| 1 | 1 3 4 3 1 | 3 5 9 7 2 | 5 12 17 14 4 | 12 22 38 28 8 |
| 2 | 3 5 3 1 0 | 5 12 7 2 0 | 12 22 14 4 0 | 22 50 28 8 0 |
| 3 | 3 6 3 0 0 | 6 12 8 0 0 | 12 26 14 0 0 | 26 50 32 0 0 |
| 4 | 2 4 4 2 0 | 4 8 8 6 2 | 8 16 18 10 0 | 16 34 34 24 0 |
| 5 | 1 2 3 4 2 | 2 4 6 8 6 | 4 8 12 18 10 | 8 16 26 34 24 |
| 6 | 1 3 4 3 1 | 3 5 9 7 2 | 5 12 17 14 4 | 12 22 38 28 8 |
| 7 | 1 3 5 3 0 | 3 6 9 8 0 | 6 12 20 14 0 | 12 26 38 32 0 |
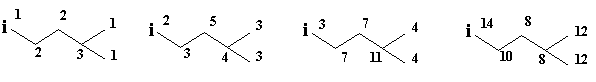
| ||||
| {1W} | {2W} | {3W} | {DS} | (a) |
|
Ws (i) = 7+7/2+11/3+8/4 ≈ 16.167;
XLDS(i) = 14∙100+10∙10-2+8∙10-4+8∙10-6+12∙10-8+12∙10-10 = 14.1008081212 ≈ 14.101; | (b) | |||
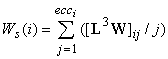
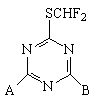
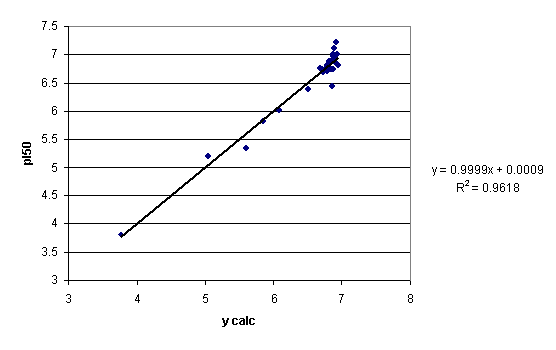
| No | A | B | NA | NB | Ws,A | Ws,B | XA* | XB | VA** | VB | pI50 |
| 1 | NH2 | NH2 | 1 | 1 | 1 | 1 | 1.1 | 1.1 | 18.763 | 18.763 | 3.82 |
| 2 | NH2 | NHCH3 | 1 | 2 | 1 | 5 | 1.1 | 3.23 | 18.763 | 32.636 | 5.20 |
| 3 | NH2 | NHC2H5 | 1 | 3 | 1 | 8.5 | 1.1 | 6.446 | 18.763 | 47.908 | 5.34 |
| 4 | NH2 | NH-i-C3H7 | 1 | 4 | 1 | 13.66 | 1.1 | 9.061 | 18.763 | 60.766 | 5.83 |
| 5 | NHCH3 | NHCH3 | 2 | 2 | 5 | 5 | 3.23 | 3.23 | 32.636 | 32.636 | 6.01 |
| 6 | NHCH3 | NHC2H5 | 2 | 3 | 5 | 8.5 | 3.23 | 6.446 | 32.636 | 47.908 | 6.39 |
| 7 | NHCH3 | NHC3H7 | 2 | 4 | 5 | 11.75 | 3.23 | 10.071 | 32.636 | 62.393 | 6.75 |
| 8 | NHCH3 | NH-i-C3H7 | 2 | 4 | 5 | 13.66 | 3.23 | 9.061 | 32.636 | 60.766 | 6.76 |
| 9 | NHCH3 | NHC4H9 | 2 | 5 | 5 | 13.93 | 3.23 | 15.111 | 32.636 | 76.638 | 6.74 |
| 10 | NHCH3 | NH-s-C4H9 | 2 | 5 | 5 | 15.16 | 3.23 | 13.091 | 32.636 | 75.039 | 6.76 |
| 11 | NHCH3 | NH-t-C4H9 | 2 | 5 | 5 | 20.50 | 3.23 | 12.081 | 32.636 | 74.106 | 6.78 |
| 12 | NHCH3 | NHC5H11 | 2 | 6 | 5 | 15.62 | 3.23 | 21.161 | 32.636 | 88.241 | 7.12 |
| 13 | NHC2H5 | NHC2H5 | 3 | 3 | 8.5 | 8.5 | 6.446 | 6.446 | 47.908 | 47.908 | 6.82 |
| 14 | NHC2H5 | NHC3H7 | 3 | 4 | 8.5 | 11.75 | 6.446 | 10.071 | 47.908 | 62.393 | 6.74 |
| 15 | NHC2H5 | NH-i-C3H7 | 3 | 4 | 8.5 | 13.66 | 6.446 | 9.061 | 47.908 | 60.766 | 6.89 |
| 16 | NHC2H5 | NHC4H9 | 3 | 5 | 8.5 | 13.93 | 6.446 | 15.111 | 47.908 | 76.638 | 6.95 |
| 17 | NHC2H5 | NH-i-C4H9 | 3 | 5 | 8.5 | 16.16 | 6.446 | 14.101 | 47.908 | 74.497 | 7.01 |
| 18 | NHC2H5 | NH-s-C4H9 | 3 | 5 | 8.5 | 15.16 | 6.446 | 13.091 | 47.908 | 75.039 | 6.87 |
| 19 | NHC2H5 | NH-t-C4H9 | 3 | 5 | 8.5 | 20.50 | 6.446 | 12.081 | 47.908 | 74.106 | 6.97 |
| 20 | NHC2H5 | NHC5H11 | 3 | 6 | 8.5 | 15.62 | 6.446 | 21.161 | 47.908 | 88.241 | 6.94 |
| 21 | NHC2H5 | NHC6H13 | 3 | 7 | 8.5 | 17.00 | 6.446 | 28.222 | 47.908 | 102.032 | 7.21 |
| 22 | NHC2H5 | NHC7H15 | 3 | 8 | 8.5 | 18.17 | 6.446 | 36.292 | 47.908 | 116.672 | 7.01 |
| 23 | NHC2H5 | NHC8H17 | 3 | 9 | 8.5 | 19.18 | 6.446 | 45.373 | 47.908 | 128.770 | 6.81 |
| 24 | NHC3H7 | NHC3H7 | 4 | 4 | 11.75 | 11.75 | 10.071 | 10.071 | 62.393 | 62.393 | 6.45 |
| 25 | NH-i-C3H7 | NHC3H7 | 4 | 4 | 13.66 | 11.75 | 9.061 | 10.071 | 60.766 | 62.393 | 6.75 |
| 26 | NH-i-C3H7 | NH-i-C3H7 | 4 | 4 | 13.66 | 13.66 | 9.061 | 9.061 | 60.766 | 60.766 | 6.75 |
| 27 | NH-i-C3H7 | NHC4H9 | 4 | 5 | 13.66 | 13.93 | 9.061 | 15.111 | 60.766 | 76.638 | 6.71 |
| 28 | NH-i-C3H7 | NH-s-C4H9 | 4 | 5 | 13.66 | 15.16 | 9.061 | 13.091 | 60.766 | 75.039 | 6.88 |
| 29 | NH-i-C3H7 | NH-t-C4H9 | 4 | 5 | 13.66 | 20.50 | 9.061 | 12.081 | 60.766 | 74.106 | 6.70 |
| 30 | NH-i-C3H7 | NHC5H11 | 4 | 6 | 13.66 | 15.62 | 9.061 | 21.161 | 60.766 | 88.241 | 6.69 |
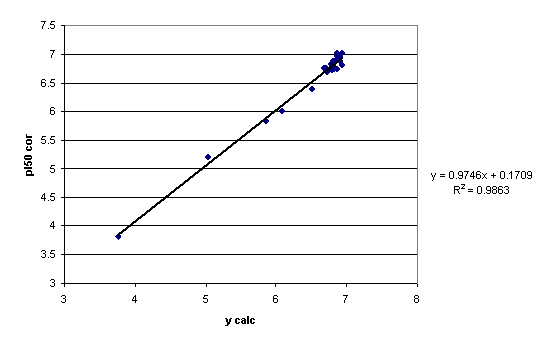
| No. | XI | bi | A | r | s | v(%) | F |
| 1 | 1/N,B | -3.786 | 7.549 | 0.8987 | 0.311 | 4.752 | 117.587 |
| 2 | 1/Ws,B | -3.372 | 6.933 | 0.8298 | 0.396 | 6.047 | 61.899 |
| 3 | 1/XB | -3.806 | 7.038 | 0.8835 | 0.333 | 5.076 | 99.598 |
| 4 | 1/VB | -72.276 | 7.760 | 0.8975 | 0.313 | 4.779 | 115.936 |
| 5 | 1/NA1/NB | -1.234-2.678 | 7.810 | 0.9577 | 0.208 | 3.175 | 149.557 |
| 6 | 1/Ws,A1/Ws,B | -1.335-2.077 | 7.118 | 0.9615 | 0.199 | 3.030 | 165.554 |
| 7 | 1/XA1/XB | -1.317-2.526 | 7.252 | 0.9662 | 0.186 | 2.844 | 189.755 |
| 8 | 1/VA1/VB | -22.999-52.514 | 8.048 | 0.9478 | 0.231 | 3.519 | 119.237 |
| 9 | 1/Ws,A1/VB | -1.114-47.194 | 7.618 | 0.9714 | 0.172 | 2.619 | 226.162 |
| 10 | 1/Ws,A1/XB | -1.180-2.458 | 7.159 | 0.9729 | 0.167 | 2.550 | 239.280 |
| 11 | 1/Ws,A1/NB | -1.120-2.484 | 7.484 | 0.9746 | 0.162 | 2.472 | 255.491 |
| 12 | NA1/NA1/NB | -0.385-2.777-2.444 | 9.477 | 0.9834 | 0.134 | 2.039 | 254.937 |
| 13 | Ws,A1/Ws,A1/Ws,B | -0.025-1.594-2.056 | 7.372 | 0.9661 | 0.190 | 2.903 | 121.327 |
| 14 | XA1/XA1/XB | -0.078-2.047-2.413 | 7.876 | 0.9818 | 0.140 | 2.132 | 232.401 |
| 15 | VA1/VA1/VB | -0.036-65.998-45.367 | 10.649 | 0.9808 | 0.144 | 2.193 | 219.227 |
| 16 | XA1/VA1/VB | -0.155-59.011-46.244 | 9.762 | 0.9815 | 0.141 | 2.152 | 228.039 |
| 17 | XA1/VA1/XB | -0.154-60.818-2.399 | 9.337 | 0.9836 | 0.133 | 2.029 | 257.426 |
| 18 | XA1/VA1/NB | -0.153-58.888-2.430 | 9.614 | 0.9846 | 0.129 | 1.968 | 274.318 |
| No. | Xi | bi | a | r | s | v(%) | F |
| 1 | 1/Ws,harloo*ycor** | -3.151 | 7.121 | 0.9553 0.9467 0.9666 | 0.210 0.229 0.175 | 3.204 3.489 2.669 | 292.215 398.721 |
| 2 | 1/Xgeolooycor | -3.891 | 7.253 | 0.9621 0.9558 0.9793 | 0.194 0.209 0.138 | 2.956 3.183 2.108 | 348.097 655.776 |
| 3 | 1/VharNharlooycor | -126.800 -0.541 | 11.091 | 0.9763 0.9721 0.9924 | 0.156 0.167 0.086 | 2.387 2.543 1.307 | 275.063 875.466 |
| 4 | 1/VharXharlooycor | -113.340 -0.137 | 10.010 | 0.9777 0.9735 0.9907 | 0.152 0.163 0.095 | 2.318 2.480 1.446 | 292.278 713.286 |
| 5 | 1/NharXharWs,harlooycor | -5.614 -0.056 -0.057 | 9.491 | 0.9798 0.9742 0.9918 | 0.147 0.160 0.091 | 2.247 2.446 1.380 | 208.342 523.336 |
| 6 | 1/VharXharWs,harlooycor | -119.503 -0.097 -0.047 | 10.292 | 0.9807 0.9752 0.9938 | 0.144 0.157 0.079 | 2.198 2.397 1.204 | 218.158 690.328 |
| 7 | 1/VharXharWs,harNharlooycor | -105.131 -0.232 -0.081 0.673 | 9.058 | 0.9824 0.9742 0.9938 | 0.141 0.160 0.080 | 2.144 2.444 1.226 | 172.608 499.253 |
| 8 | 1/NharXharWs,harVharlooycor | -4.724 -0.228 -0.070 0.052 | 7.858 | 0.9825 0.9751 0.9924 | 0.140 0.157 0.089 | 2.139 2.401 1.358 | 173.400 405.773 |
| (1) | t = (vi)1≤i≤n is named terminal path if: vi Î V, t Î P(G) and " v Î V s. th. (vn, v) Î E then t È (vn, v) Ï P(G) |
| (2) | T(G)i = {t = (vi)1≤i≤n s. th. v1 = i and t terminal path} |

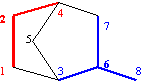
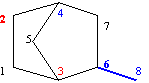
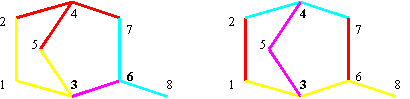
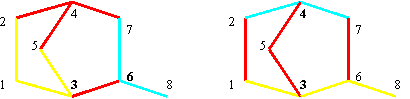
| (3) | } | {1, 2, 4, 5, 3, 6, 7, 8}, {1, 2, 4, 7, 8}, {1, 2, 4, 7, 6, 3, 5}, {1, 3, 6, 7, 8}, {1, 3, 6, 7, 4, 2}, {1, 3, 6, 7, 4, 5}, {1, 3, 5, 4, 7, 6}, {1, 3, 5, 4, 7, 8}, {1, 3, 5, 4, 2} |
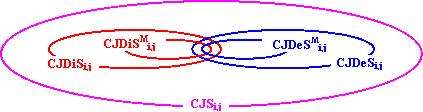
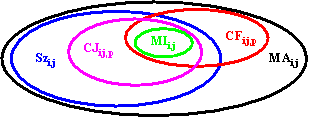
| (4) | CJi,j,p = {k : k Î V} is named CJ set of i vs. j and p if: d(G)k,i < d(G)k,j $ q Î Pk,i s. th. p Ç q = {i} |
| (5) | CJDii,j,p = {k : k Î V} is named CJDi set of i vs. j and p if: CJDii,j,p Î CJSi,j l(p) = d(G)i,j |
| (6) | CJDei,j,p = {k | k Î V} is named CJDe set of i vs. j and p if: CJDii,j,p Î CJSi,j l(p) = δ(G)i,j |
| (7) | CJDii,j,p = Æ; CJDij,i,p = Æ;
For (v = 1; v ≤ |V|; v++)
If (d(G)v,j < d(G)v,i) and ($p' Î P(G)v,j s.th. p' Ç p == {j}) then
|
| (8) | CJDiSMi,j Í CJDiSi,j Í CJSi,j and CJDeSMi,j Í CJDeSi,j Í CJSi,j |
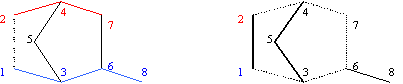
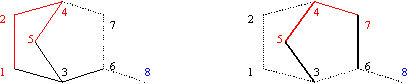
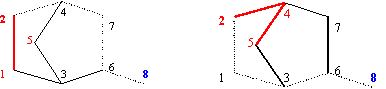
| (9) | Gp = (Vp, Ep), Vp = {v Î V : v Ï p\{i, j}}, Ep = {e = (ea, eb) Î E : ea, eb Ï p\{i, j}} |

| (10) | CFi,j,p = {k : k Î V} is named CF fragment of i vs. j and p if: d(Gp)k,i < d(Gp)k,j |
| (11) | " k Î CFSi,j,p, $ q Î P(Gp)k.i path from k to i in Gp s. th. q Ç p = {i} |
| (12) | CFDii,j,p={k : k Î V} is named CFDi fragment of i vs. j and p if: CFDii,j,p Î CFSi,j l(p) = d(Gp)i,j |
| (13) | CFDei,j,p={k : k Î V} is named CFDe fragment of i vs. j and p if: CFDei,j,p Î CFSi,j l(p) = δ(Gp)i,j |
| (14) | CFDii,j,p = Æ; CFDij,i,p = Æ;
For (v = 1; v ≤ |V|; v++)
If (d(Gp)v,j < d(Gp)v,i) then
|
| (15) | CFDiSMi,j Í CFDiSi,j Í CFSi,j and CFDeSMi,j Í CFDeSi,j Í CFSi,j |
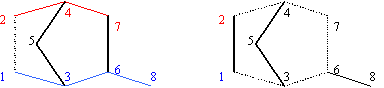

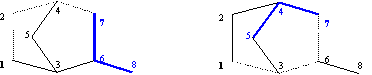
| (16) | SzDii,j = {k : k Î V} is named SzDi fragment of i vs. j if: d(G)k,i < d(G)k,j |
| (17) | CJDi Í SzDi, |
| (18) | CFDi Ë SzDi, |
| (19) |
For (i = 1; i < |X|; i++)
For (v = 1; v ≤ |X|; v++)
For (ct Î T(G)v)
If (ct[k] == j)and(dvj > k) then
If dvi > dvj then
If dvi > dvj then
|
| (20) | SzDii,j = {k : k Î V} is named SzDe set of i vs. j if: δ(G)k,i < δ(G)k,j |
| (21) | MIi,j = {i} |
| (22) | MAi,j = G\{j} |
| (23) | MIi,j Í CJi,j,p; MIi,j Í CFi,j,p; MIi,j Í Szi,j |
| (24) | CJi,j,p Ê MAi,j; CFi,j,p Ê MAi,j; Szi,j Ê MAi,j |


| (25) | d(Gp)k,i < ¥ Þ $ pv,k Î P(Gp)v,k (pv,k Í pv,i) |
| (26) | d(Gp)k,j = ¥ |
| (27) | CFi,j,p connected |
| (28) | $ pk,i Î P(Gp)k,i (pk,i Í pv,i) , $ pv,k Î P(Gp)v,k (pv,k Í pv,i) |
| (29) | v connected with i in CFi,j,p Þ CFi,j,p connected |
| (30) | $ pk,i Î P(G)k,i (pk,i Í pv,i) , $ pv,k Î P(G)v,k (pv,k Í pv,i) |
| d(G)v,i < d(G)v,j | (31) |
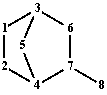
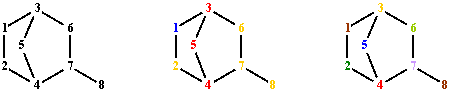
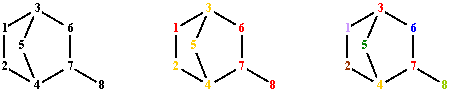
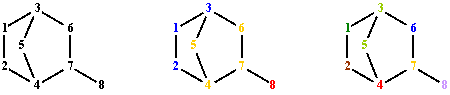
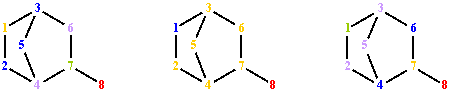
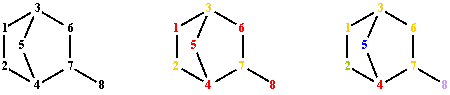
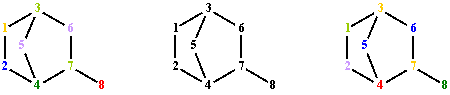
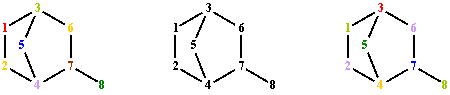
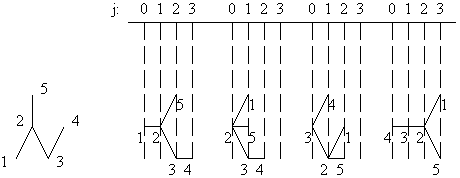
T(G)1 1 2 4 5 3 6 7 8 1 2 4 7 8 1 2 4 7 6 3 5 1 3 6 7 8 1 3 6 7 4 2 1 3 6 7 4 5 1 3 5 4 7 6 1 3 5 4 7 8 1 3 5 4 2Fig. 2. Terminal paths of graph G from fig. 1 starting from vertex 1
| APS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | LAPS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | |
| 1 | 2 | 3 | 4 | 7 | 6 | 2 | 1 | 25 | 97 | 1=σ(8) | 1 | 2 | 3 | 4 | 5 | 5 | 2 | 22 | 99 | |
| 2 | 2 | 3 | 5 | 5 | 6 | 4 | 0 | 25 | 97 | 2=σ(1) | 2 | 3 | 4 | 7 | 6 | 2 | 1 | 25 | 97 | |
| 3 | 3 | 3 | 5 | 7 | 3 | 0 | 0 | 21 | 67 | 3=σ(2) | 2 | 3 | 5 | 5 | 6 | 4 | 0 | 25 | 97 | |
| 4 | 3 | 4 | 4 | 6 | 3 | 1 | 0 | 21 | 68 | 4=σ(6) | 2 | 4 | 4 | 5 | 6 | 3 | 0 | 24 | 90 | |
| 5 | 2 | 4 | 5 | 5 | 4 | 5 | 1 | 26 | 102 | 5=σ(5) | 2 | 4 | 5 | 5 | 4 | 5 | 1 | 26 | 102 | |
| 6 | 2 | 4 | 4 | 5 | 6 | 3 | 0 | 24 | 90 | 6=σ(7) | 3 | 3 | 4 | 5 | 5 | 2 | 0 | 22 | 78 | |
| 7 | 3 | 3 | 4 | 5 | 5 | 2 | 0 | 22 | 78 | 7=σ(3) | 3 | 3 | 5 | 7 | 3 | 0 | 0 | 21 | 67 | |
| 8 | 1 | 2 | 3 | 4 | 5 | 5 | 2 | 22 | 99 | 8=σ(4) | 3 | 4 | 4 | 6 | 3 | 1 | 0 | 21 | 68 |
| DPS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | LDPS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | |
| 1 | 2 | 3 | 2 | 2 | 0 | 0 | 0 | 9 | 22 | 1=σ(8) | 1 | 2 | 3 | 2 | 0 | 0 | 0 | 8 | 22 | |
| 2 | 2 | 3 | 3 | 0 | 0 | 0 | 0 | 8 | 17 | 2=σ(1) | 2 | 3 | 2 | 2 | 0 | 0 | 0 | 9 | 22 | |
| 3 | 3 | 3 | 1 | 0 | 0 | 0 | 0 | 7 | 12 | 3=σ(2) | 2 | 3 | 3 | 0 | 0 | 0 | 0 | 8 | 17 | |
| 4 | 3 | 4 | 0 | 0 | 0 | 0 | 0 | 7 | 11 | 4=σ(5) | 2 | 4 | 1 | 0 | 0 | 0 | 0 | 7 | 13 | |
| 5 | 2 | 4 | 1 | 0 | 0 | 0 | 0 | 7 | 13 | 5=σ(6) | 2 | 4 | 2 | 0 | 0 | 0 | 0 | 8 | 16 | |
| 6 | 2 | 4 | 2 | 0 | 0 | 0 | 0 | 8 | 16 | 6=σ(3) | 3 | 3 | 1 | 0 | 0 | 0 | 0 | 7 | 12 | |
| 7 | 3 | 3 | 2 | 0 | 0 | 0 | 0 | 8 | 15 | 7=σ(7) | 3 | 3 | 2 | 0 | 0 | 0 | 0 | 8 | 15 | |
| 8 | 1 | 2 | 3 | 2 | 0 | 0 | 0 | 8 | 22 | 8=σ(4) | 3 | 4 | 0 | 0 | 0 | 0 | 0 | 7 | 11 |
| ΔPS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | LΔPS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | |
| 1 | 0 | 0 | 0 | 1 | 4 | 2 | 1 | 8 | 43 | 1=σ(1) | 0 | 0 | 0 | 1 | 4 | 2 | 1 | 8 | 43 | |
| 2 | 0 | 0 | 0 | 1 | 4 | 4 | 0 | 9 | 48 | 2=σ(6) | 0 | 0 | 0 | 1 | 4 | 3 | 0 | 8 | 42 | |
| 3 | 0 | 0 | 2 | 4 | 3 | 0 | 0 | 9 | 37 | 3=σ(2) | 0 | 0 | 0 | 1 | 4 | 4 | 0 | 9 | 48 | |
| 4 | 0 | 0 | 2 | 4 | 2 | 1 | 0 | 9 | 38 | 4=σ(5) | 0 | 0 | 0 | 4 | 0 | 4 | 1 | 9 | 47 | |
| 5 | 0 | 0 | 0 | 4 | 0 | 4 | 1 | 9 | 47 | 5=σ(4) | 0 | 0 | 2 | 4 | 2 | 1 | 0 | 9 | 38 | |
| 6 | 0 | 0 | 0 | 1 | 4 | 3 | 0 | 8 | 42 | 6=σ(3) | 0 | 0 | 2 | 4 | 3 | 0 | 0 | 9 | 37 | |
| 7 | 1 | 0 | 0 | 1 | 4 | 2 | 0 | 8 | 37 | 7=σ(8) | 1 | 0 | 0 | 0 | 1 | 4 | 2 | 8 | 44 | |
| 8 | 1 | 0 | 0 | 0 | 1 | 4 | 2 | 8 | 44 | 8=σ(7) | 1 | 0 | 0 | 1 | 4 | 2 | 0 | 8 | 37 |
| ATS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | LATS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | |
| 1 | 0 | 0 | 0 | 3 | 4 | 1 | 1 | 9 | 45 | 1=σ(8) | 0 | 0 | 0 | 0 | 1 | 3 | 2 | 6 | 37 | |
| 2 | 0 | 0 | 1 | 1 | 3 | 4 | 0 | 9 | 46 | 2=σ(1) | 0 | 0 | 0 | 3 | 4 | 1 | 1 | 9 | 45 | |
| 3 | 0 | 0 | 1 | 5 | 3 | 0 | 0 | 9 | 38 | 3=σ(5) | 0 | 0 | 1 | 1 | 0 | 4 | 1 | 7 | 38 | |
| 4 | 0 | 1 | 0 | 3 | 2 | 1 | 0 | 7 | 30 | 4=σ(2) | 0 | 0 | 1 | 1 | 3 | 4 | 0 | 9 | 46 | |
| 5 | 0 | 0 | 1 | 1 | 0 | 4 | 1 | 7 | 38 | 5=σ(3) | 0 | 0 | 1 | 5 | 3 | 0 | 0 | 9 | 38 | |
| 6 | 0 | 1 | 0 | 0 | 3 | 3 | 0 | 7 | 35 | 6=σ(6) | 0 | 1 | 0 | 0 | 3 | 3 | 0 | 7 | 35 | |
| 7 | 1 | 0 | 0 | 1 | 3 | 2 | 0 | 7 | 32 | 7=σ(4) | 0 | 1 | 0 | 3 | 2 | 1 | 0 | 7 | 30 | |
| 8 | 0 | 0 | 0 | 0 | 1 | 3 | 2 | 6 | 37 | 8=σ(7) | 1 | 0 | 0 | 1 | 3 | 2 | 0 | 7 | 32 |
| DTS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | LDTS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | |
| 1 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | 8 | 1=σ(8) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 3 | 2=σ(1) | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | 8 | |
| 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 3 | 3=σ(3) | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 3 | |
| 4 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 4=σ(5) | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 3 | |
| 5 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 3 | 5=σ(2) | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 3 | |
| 6 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 6=σ(4) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | |
| 7 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 7=σ(6) | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8=σ(7) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| ΔTS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | LΔTS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | |
| 1 | 0 | 0 | 0 | 0 | 2 | 1 | 1 | 4 | 23 | 1=σ(8) | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 4 | 26 | |
| 2 | 0 | 0 | 0 | 0 | 1 | 4 | 0 | 5 | 29 | 2=σ(5) | 0 | 0 | 0 | 0 | 0 | 3 | 1 | 4 | 25 | |
| 3 | 0 | 0 | 0 | 2 | 3 | 0 | 0 | 5 | 23 | 3=σ(6) | 0 | 0 | 0 | 0 | 1 | 3 | 0 | 4 | 23 | |
| 4 | 0 | 0 | 0 | 2 | 1 | 1 | 0 | 4 | 19 | 4=σ(2) | 0 | 0 | 0 | 0 | 1 | 4 | 0 | 5 | 29 | |
| 5 | 0 | 0 | 0 | 0 | 0 | 3 | 1 | 4 | 25 | 5=σ(1) | 0 | 0 | 0 | 0 | 2 | 1 | 1 | 4 | 23 | |
| 6 | 0 | 0 | 0 | 0 | 1 | 3 | 0 | 4 | 23 | 6=σ(4) | 0 | 0 | 0 | 2 | 1 | 1 | 0 | 4 | 19 | |
| 7 | 1 | 0 | 0 | 0 | 2 | 2 | 0 | 5 | 23 | 7=σ(3) | 0 | 0 | 0 | 2 | 3 | 0 | 0 | 5 | 23 | |
| 8 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 4 | 26 | 8=σ(7) | 1 | 0 | 0 | 0 | 2 | 2 | 0 | 5 | 23 |
| AVS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | LAVS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | |
| 1 | 3 | 6 | 7 | 8 | 8 | 8 | 8 | 48 | 212 | 1=σ(8) | 2 | 4 | 7 | 8 | 8 | 8 | 8 | 45 | 207 | |
| 2 | 3 | 6 | 8 | 8 | 8 | 8 | 8 | 49 | 215 | 2=σ(1) | 3 | 6 | 7 | 8 | 8 | 8 | 8 | 48 | 212 | |
| 3 | 4 | 7 | 8 | 8 | 8 | 8 | 8 | 51 | 218 | 3=σ(2) | 3 | 6 | 8 | 8 | 8 | 8 | 8 | 49 | 215 | |
| 4 | 4 | 8 | 8 | 8 | 8 | 8 | 8 | 52 | 220 | 4=σ(5) | 3 | 7 | 8 | 8 | 8 | 8 | 8 | 50 | 217 | |
| 5 | 3 | 7 | 8 | 8 | 8 | 8 | 8 | 50 | 217 | 5=σ(6) | 3 | 7 | 8 | 8 | 8 | 8 | 8 | 50 | 217 | |
| 6 | 3 | 7 | 8 | 8 | 8 | 8 | 8 | 50 | 217 | 6=σ(3) | 4 | 7 | 8 | 8 | 8 | 8 | 8 | 51 | 218 | |
| 7 | 4 | 7 | 8 | 8 | 8 | 8 | 8 | 51 | 218 | 7=σ(7) | 4 | 7 | 8 | 8 | 8 | 8 | 8 | 51 | 218 | |
| 8 | 2 | 4 | 7 | 8 | 8 | 8 | 8 | 45 | 207 | 8=σ(4) | 4 | 8 | 8 | 8 | 8 | 8 | 8 | 52 | 220 |
| DVS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | LDVS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | |
| 1 | 2 | 3 | 1 | 1 | 0 | 0 | 0 | 7 | 15 | 1=σ(8) | 1 | 2 | 3 | 1 | 0 | 0 | 0 | 7 | 18 | |
| 2 | 2 | 3 | 2 | 0 | 0 | 0 | 0 | 7 | 14 | 2=σ(1) | 2 | 3 | 1 | 1 | 0 | 0 | 0 | 7 | 15 | |
| 3 | 3 | 3 | 1 | 0 | 0 | 0 | 0 | 7 | 12 | 3=σ(2) | 2 | 3 | 2 | 0 | 0 | 0 | 0 | 7 | 14 | |
| 4 | 3 | 4 | 0 | 0 | 0 | 0 | 0 | 7 | 11 | 4=σ(5) | 2 | 4 | 1 | 0 | 0 | 0 | 0 | 7 | 13 | |
| 5 | 2 | 4 | 1 | 0 | 0 | 0 | 0 | 7 | 13 | 5=σ(6) | 2 | 4 | 1 | 0 | 0 | 0 | 0 | 7 | 13 | |
| 6 | 2 | 4 | 1 | 0 | 0 | 0 | 0 | 7 | 13 | 6=σ(3) | 3 | 3 | 1 | 0 | 0 | 0 | 0 | 7 | 12 | |
| 7 | 3 | 3 | 1 | 0 | 0 | 0 | 0 | 7 | 12 | 7=σ(7) | 3 | 3 | 1 | 0 | 0 | 0 | 0 | 7 | 12 | |
| 8 | 1 | 2 | 3 | 1 | 0 | 0 | 0 | 7 | 18 | 8=σ(4) | 3 | 4 | 0 | 0 | 0 | 0 | 0 | 7 | 11 |
| ΔVS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | LΔVS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | |
| 1 | 0 | 0 | 0 | 1 | 3 | 2 | 1 | 7 | 38 | 1=σ(1) | 0 | 0 | 0 | 1 | 3 | 2 | 1 | 7 | 38 | |
| 2 | 0 | 0 | 0 | 1 | 3 | 3 | 0 | 7 | 37 | 2=σ(2) | 0 | 0 | 0 | 1 | 3 | 3 | 0 | 7 | 37 | |
| 3 | 0 | 0 | 1 | 3 | 3 | 0 | 0 | 7 | 30 | 3=σ(6) | 0 | 0 | 0 | 1 | 3 | 3 | 0 | 7 | 37 | |
| 4 | 0 | 0 | 1 | 3 | 2 | 1 | 0 | 7 | 31 | 4=σ(5) | 0 | 0 | 0 | 2 | 0 | 4 | 1 | 7 | 39 | |
| 5 | 0 | 0 | 0 | 2 | 0 | 4 | 1 | 7 | 39 | 5=σ(4) | 0 | 0 | 1 | 3 | 2 | 1 | 0 | 7 | 31 | |
| 6 | 0 | 0 | 0 | 1 | 3 | 3 | 0 | 7 | 37 | 6=σ(3) | 0 | 0 | 1 | 3 | 3 | 0 | 0 | 7 | 30 | |
| 7 | 1 | 0 | 0 | 1 | 3 | 2 | 0 | 7 | 32 | 7=σ(8) | 1 | 0 | 0 | 0 | 1 | 3 | 2 | 7 | 38 | |
| 8 | 1 | 0 | 0 | 0 | 1 | 3 | 2 | 7 | 38 | 8=σ(7) | 1 | 0 | 0 | 1 | 3 | 2 | 0 | 7 | 32 |
| ACS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | LACS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ΣiSi,j | ΣiSi,j∙i | |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 2 | 11 | 1=σ(8) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 2 | 11 | 2=σ(1) | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 2 | 11 | |
| 3 | 0 | 0 | 0 | 2 | 1 | 0 | 0 | 3 | 16 | 3=σ(2) | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 2 | 11 | |
| 4 | 0 | 0 | 0 | 2 | 1 | 0 | 0 | 3 | 16 | 4=σ(6) | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 2 | 11 | |
| 5 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | 10 | 5=σ(7) | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 2 | 11 | |
| 6 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 2 | 11 | 6=σ(5) | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 2 | 10 | |
| 7 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 2 | 11 | 7=σ(3) | 0 | 0 | 0 | 0 | 2 | 1 | 0 | 3 | 16 | |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8=σ(4) | 0 | 0 | 0 | 0 | 2 | 1 | 0 | 3 | 16 |