Free Software Development. 4. Client-Server Implementation of Bone Age Assessment Calculations from Leonardo Electronic Journal of Practices and Technologies

Free Software Development. 4.

Client-Server Implementation of Bone Age Assessment Calculations

Sorana BOLBOACĂ^a*, Carmencita DENEŞ^b, Andrei ACHIMAŞ CADARIU^a

^a “Iuliu Haţieganu” University of Medicine and Pharmacy, Cluj-Napoca, Romania

^b “Axente Iancu” Pediatric Clinic no. 1, Cluj-Napoca, Romania

* corresponding author, sbolboaca@umfcluj.ro

Abstract

In pediatrics, bone age also called skeletal maturity, an expression of biological maturity of a child, is an important quantitative measure for the clinical diagnosis of endocrinological problems and growth disorders.

The present paper discusses a Java script implementation of Tanner-Whitehouse Method on computer, with complete graphical interface that include pictures and explanations for every bone. The program allows to select a stage (from a set of 7 or 8 stages) for every bone (from a set of 20 bones), and also allow user to input some specific data such as natural age, sex, place of residence. Based on TW2 reported values, selected and input data, the program compute the bone age.

Java script functions and objects were used in order to make an efficient and adaptive program. Note that in classic way, the program implementation it requires more than 160 groups of instructions only for user interface design. Using of dynamic creation of page, the program became smaller and efficient.

The program was tested and put on a web server to serve for directly testing via http service and from where can also be download and runes from a personal computer without internet connection:

http://vl.academicdirect.ro/medical_informatics/bone_age/v1.0/

Keywords

Bone age, Skeletal maturity, Tanner-Whitehouse method, Online evaluation, Java script programming.

Background

In pediatrics, skeletal maturity, also called “bone age”, an expression of biological maturity of a child, is an important quantitative measure for the clinical diagnosis of endocrinological problems and growth disorders. Bone age is also used in monitoring children with hormone therapy.

Skeletal maturity may be assessed by analysis of the ossification centers of the hand, foot, knee, elbow or pelvis but most often used is the hand.

For the assessment of child skeletal maturity, radiologists use a hand and wrist radiography.

The assessment is realized by assessing the ossification and maturation of the epiphysis of the hands and wrists comparing them with standards radiographs and standards descriptions. There are al least two methods of evaluating wrist and hand bone age represented by Tanner-Whitehouse method and Greulich-Pyle method.[1],[2]

In the Greulich-Pyle [3] method the radiographs of the whole hand and wrist are compared with images in the atlas. This method, as the Tanner-Whitehouse one, is gender specific and it is enabling to assess the bone age of the child from birth to 18 years old. The Greulich-Pyle method has been used more frequently by orthopedists.

The Tanner and Whitehouse method [4] is most frequently applied methods for skeletal maturity in Romania. The Tanner-Whitehouse method is based on left hand and wrist radiography. Generally, in order to determine the bone age it is used the left hand and wrist radiography. The bone age of the left hand precedes that of the right hand because the right hand is more frequently involved in injury than the left one [5]. The score is assign to 20 of the epiphyses in the left hand and wrist radiographs compared with the standard.

In the end, the radiologist totals the scores for those 20 bones and, by reference to gender-dependent standard tables, converts the total maturity score (on a scale of 0 to 1000) into an individual bone age. Comparing the bone age with chronological age will reveal if the child growth is advanced or retarded relative to the normal situation.

The Grulich-Pyle method and the Tanner-Whitehouse method do not give equivalent bone ages [6].

Estimating bone age of a child using Tanner-Whitehouse method is time-consuming (between 8 and 10 minutes for each patient) and is also necessary that the radiologists to have some abilities and a lot of practice. In recent years, the increasing speed in computer sciences and decreases their costs give the opportunity to create and use computerized bone age estimation system.

In order to help radiologists to estimate bone age, we created and present in this paper software which use the Tanner-Whitehouse method for estimating child bone age.

Tanner-Whitehouse Method

To assess the bone age the Tanner-Whitehouse method were used [4]. For this method is necessary to analyze 20 bones: distal radius, distal ulna, first, third and fifth metacarpals, proximal phalanges of the thumb, third and fifth fingers, middle phalanges of the third and fifth fingers, distal phalanges of the thumb, third and fifth fingers, the seventh carpal bones: capitate, hamate, triquetral, lunate, scaphoid, trapezium and trapezoid.

Each bone, conform to Tanner-Whitehouse method, was graded into 8 or 9 maturity stages. Staging were assigned pursuant the rating system of the Tanner-Whitehouse method. If no sign of the bone was presented, the lowest rating was given (this rate in not include in our software).

The epiphyseal region were staging by distinction of the size, shape, density, smoothness or thickening of the borders, thickness of epiphyseal line, extent of fusion and capping. The individual scores of 20 bones corresponding to the stages, both for the boys and for the girls are given in table 1 and table 2.

For computing bone age we used, according to the reference table (table 3 and table 4), Tanner-Whitehouse equivalency between maturity score and bone age [4].

All data from table 1-4 are writes in PHP modules. More, photos with all stages of grow for bones are also scanned and putted into a web folder.

Table 1. Twenty Bone Tanner-Whitehouse Maturity Score for Boys

Bone	Boys
Bone	B	C	D	E	F	G	H	I
Radius	15	17	21	27	48	77	96	106
Ulna	22	26	30	39	56	73	84	X
First Metacarpal	4	5	11	19	24	28	30	32
Third Metacarpal	3	4	6	10	16	22	23	25
Fifth Metacarpal	3	3	6	12	17	21	23	25
Proximal Phalanx of the Thumb	4	5	8	15	23	28	30	32
Proximal Phalanx of the Third Finger	3	4	6	13	20	23	24	26
Proximal Phalanx of the Fifth Finger	3	3	6	13	19	22	23	25
Middle Phalanx of the Third Finger	3	4	7	13	19	22	23	25
Middle Phalanx of the Fifth Finger	4	4	8	14	19	21	22	23
Distal Phalanx of the Thumb	4	4	7	14	23	30	31	33
Distal Phalanx of the Third Finger	3	4	6	10	16	21	22	24
Distal Phalanx of the Fifth Finger	3	4	7	11	16	20	21	23
Capitate	60	62	65	71	79	89	116	X
Hamate	42	44	49	59	70	81	92	106
Triquetral	7	10	17	28	38	45	62	X
Lunate	10	13	20	27	36	44	60	X
Scaphoid	14	18	23	30	35	42	58	X
Trapezium	12	15	21	28	34	39	47	59
Trapezoid	14	16	20	23	32	39	56	X

Table 2. Twenty Bone Tanner-Whitehouse Maturity Score for Girls

Bone	Girls
Bone	B	C	D	E	F	G	H	I
Radius	17	19	25	33	54	85	99	106
Ulna	22	26	30	39	60	73	80	X
First Metacarpal	5	6	11	18	24	29	31	33
Third Metacarpal	3	5	7	11	17	23	24	26
Fifth Metacarpal	3	4	7	12	18	22	24	25
Proximal Phalanx of the Thumb	5	5	8	14	24	29	30	32
Proximal Phalanx of the Third Finger	4	4	7	13	20	24	25	26
Proximal Phalanx of the Fifth Finger	4	4	7	13	19	23	24	25
Middle Phalanx of the Third Finger	4	4	7	13	20	23	24	25
Middle Phalanx of the Fifth Finger	4	5	8	14	20	22	22	23
Distal Phalanx of the Thumb	5	5	8	15	24	31	32	34
Distal Phalanx of the Third Finger	3	4	6	10	17	22	23	24
Distal Phalanx of the Fifth Finger	3	4	7	11	17	21	22	23
Capitate	53	56	61	67	76	85	113	X
Hamate	44	47	53	64	74	85	97	109
Triquetral	8	12	19	28	36	46	63	X
Lunate	10	14	20	27	35	46	60	X
Scaphoid	13	17	23	29	36	44	57	X
Trapezium	12	14	20	25	32	39	49	59
Trapezoid	13	16	20	24	31	40	57	X

Table 3. Tanner-Whitehouse Boys Bone Age (BBA) for Given Maturity Score (MS)

MS	114	116	119	123	126	129	133	136	139	142	146	150	154	159	163	168
BBA	1.0	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9	2.0	2.1	2.2	2.3	2.4	2.5
MS	172	176	181	185	190	195	200	205	210	215	220	226	231	236	242	247
BBA	2.6	2.7	2.8	2.9	3.0	3.1	3.2	3.3	3.4	3.5	3.6	3.7	3.8	3.9	4.0	4.1
MS	252	258	264	270	276	282	287	292	298	303	308	314	319	325	331	337
BBA	4.2	4.3	4.4	4.5	4.6	4.7	4.8	4.9	5.0	5.1	5.2	5.3	5.4	5.5	5.6	5.7
MS	343	349	355	360	366	372	378	384	390	396	402	409	415	422	428	435
BBA	5.8	5.9	6.0	6.1	6.2	6.3	6.4	6.5	6.6	6.7	6.8	6.9	7.0	7.1	7.2	7.3
MS	441	447	454	460	466	472	477	483	489	495	501	507	513	520	526	533
BBA	7.4	7.5	7.6	7.7	7.8	79.0	8.0	8.1	8.2	8.3	8.4	8.5	8.6	8.7	8.8	8.9
MS	540	546	553	560	566	573	580	587	594	601	608	615	622	629	636	643
BBA	9.0	9.1	9.2	9.3	9.4	9.5	9.6	9.7	9.8	9.9	10.0	10.1	10.2	10.3	10.4	10.5
MS	650	657	664	671	678	684	690	697	703	711	718	725	732	740	747	754
BBA	10.6	10.7	10.8	10.9	11.0	11.1	11.2	11.3	11.4	11.5	11.6	11.7	11.8	11.9	12.0	12.1
MS	761	768	774	781	788	795	802	809	817	823	830	836	842	849	855	861
BBA	12.2	12.3	12.4	12.5	12.6	12.7	12.8	12.9	13.0	13.1	13.2	13.3	13.4	13.5	13.6	13.7
MS	867	873	879	884	889	895	900	906	911	916	921	926	931	936	940	944
BBA	13.8	13.9	14.0	14.1	14.2	14.3	14.4	14.5	14.6	14.7	14.8	14.9	15.0	15.1	15.2	15.3
MS	948	952	956	959	963	967	970	973	976	979	981	983	985	987	989	991
BBA	15.4	15.5	15.6	15.7	15.8	15.9	16.0	16.1	16.2	16.3	16.4	16.5	16.6	16.7	16.8	16.9
MS	992	994	995	996	996	997	998	999	999	999	10³
BBA	17.0	17.1	17.2	17.3	17.4	17.5	17.6	17.7	17.8	17.9	18.0

Table 4. Tanner-Whitehouse Girls Bone Age (GBA) for Given Maturity Score

MS	131	136	140	146	152	159	163	172	179	186	192	199	206	213	220	226
GBA	1.0	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9	2.0	2.1	2.2	2.3	2.4	2.5
MS	233	240	247	253	260	267	274	281	287	293	299	303	311	317	324	331
GBA	2.6	2.7	2.8	2.9	3.0	3.1	3.2	3.3	3.4	3.5	3.6	3.7	3.8	3.9	4.0	4.1
MS	338	345	351	357	363	370	376	382	389	395	402	408	414	420	426	432
GBA	4.2	4.3	4.4	4.5	4.6	4.7	4.8	4.9	5.0	5.1	5.2	5.3	5.4	5.5	5.6	5.7
MS	438	444	450	456	462	468	474	480	485	491	497	503	510	516	522	529
GBA	5.8	5.9	6.0	6.1	6.2	6.3	6.4	6.5	6.6	6.7	6.8	6.9	7.0	7.1	7.2	7.3
MS	535	541	547	553	559	565	571	578	585	592	600	608	617	625	634	643
GBA	7.4	7.5	7.6	7.7	7.8	7.9	8.0	8.1	8.2	8.3	8.4	8.5	8.6	8.7	8.8	8.9
MS	653	662	670	680	690	700	710	721	731	742	752	762	772	783	794	803
GBA	9.0	9.1	9.2	9.3	9.4	9.5	9.6	9.7	9.8	9.9	10.0	10.1	10.2	10.3	10.4	10.5
MS	812	821	830	838	845	852	859	866	872	879	885	891	898	903	908	913
GBA	10.6	10.7	10.8	10.9	11.0	11.1	11.2	11.3	11.4	11.5	11.6	11.7	11.8	11.9	12.0	12.1
MS	918	923	928	932	937	940	944	948	953	956	960	963	966	969	972	974
GBA	12.2	12.3	12.4	12.5	12.6	12.7	12.8	12.9	13.0	13.1	13.2	13.3	13.4	13.5	13.6	13.7
MS	976	979	981	982	984	986	987	989	990	991	993	994	995	995	996	996
GBA	13.8	13.9	14.0	14.1	14.2	14.3	14.4	14.5	14.6	14.7	14.8	14.9	15.0	15.1	15.2	15.3
MS	997	997	998	998	999	999	10³
GBA	15.4	15.5	15.6	15.7	15.8	15.9	16.0

Java Script Programming

Why we choose JavaScript? We had some reasons when we chose Java Script programming language. First, we chose JavaScript language in order to create our program because is a simple programming language which can be written into HTML documents. The second reason was that JavaScript language allow interactivity with the users, especially can be used in order to create online calculators and our purpose was to create a program which to allow to the radiologists to compute, assisted by the computer, child bone age.

Arrays and multi-dimensional arrays are very useful in JavaScript. Arrays are a kind of objects in JavaScript and are dynamically created. An Array object is used to store a set of values in a single variable name. Each value is an element of the array and has an associated index number. The index number start at zero (in this case the array is empty) and can be n (case in that the length of the array is equal with n) [7].

Using Array object is possible to create one-dimensional Array objects:

var <table_name> = new Array(<table_dimension>);

a[0]

a[1]

Fig. 1. a[0] and a[1] from a = new Array(2);

One-dimensional arrays were used in our program. We used Arrays Object to create a one-dimensional table in order to create content with the bones name used in Tanner-Whitehouse method for bone age assessment:

var bone_name = new Array(20);

bone_name[0] = "Radius";

bone_name[1] = "Ulna";

bone_name[2] = "First Metacarpal";

bone_name[3] = "Third Metacarpal";

…

Two-dimensional Array objects are constructed as follows:

var <table_name> = new Array(new Array(<table_dimension>), …);

b[0][0]	b[0][1]
b[1][0]	b[1][1]	b[1][2]

Fig. 2. b[0][0], b[0][1], b[1][0], b[1][1], b[1][2] from

b = new Array(new Array(2), new Array(3));

Two-dimensional arrays were used in our program. Conform to Tanner-Whitehouse method, each bone covered eight or nine maturity stage. If no sign of the bone was presented, the lowest rating was given (this stage is not include in our program). Because we didn’t take in consideration the lowest stage, in our program we have seven or eight maturity stage for each bone. In order to create the standard definition correspond to each bone maturity stage, we used the next array object:

var std_bone_stage = new Array(new Array(8), new Array(7), …);

std_bone_stage[0][1] = "The center is just visible as a single deposit of calcium, or more rarely as multiple deposits. The border is ill-defined.";

…

std_bone_stage is a two-dimensional array with 8 columns and 20 rows and it contain strings. This example corresponds to the Radius, which has eight maturity Tanner-Whitehouse stages.

Multi-dimensional Array objects declaration syntax is similarly to the two-dimensional ones. A 3-dimensional table can be declared as follows:

var <table_name> = new Array(new Array (new Array(<table_dimension>), …);

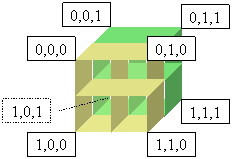
Fig. 3. c[0][0][0], c[0][0][1], c[0][1][0], c[0][1][1],

c[1][0][0], c[1][0][1], c[1][1][0], c[1][1][1] cells from

c = new Array(new Array(new Array(2)), new Array(new Array(2));

We used a 3-dimensional table for storing the bone scores that are different from boys to girls. Each bone used from Tanner-Whitehouse method has an individual score that corresponding to the stages, individual score which is different from boys and from girls. In order to use these individual scores to assess the bone age of the child, the first dimension correspond to each bone, the second one correspond to bone stage, and last one to the sex (0 for boy and 1 for girl):

var individual_bone_maturity_score =

new Array(new Array(new Array(2), …));

individual_bone_maturity_score[0][0][0]=15;

individual_bone_maturity_score[0][0][1]=17;

individual_bone_maturity_score[0][1][0]=17;

individual_bone_maturity_score[0][1][1]=19;

individual_bone_maturity_score[0][2][0]=21;

individual_bone_maturity_score[0][2][1]=25;

individual_bone_maturity_score[0][3][0]=27;

individual_bone_maturity_score[0][3][1]=33;

…

The organizing of the HTML document according to HTML 4.0 specifications (DHTML model) make possible the accessing of object containers from the document through all collection. For example, all tags with a specified format can be retrieved using the tags function:

var <variable_name> = document.all.tags(<tag_name>);

where <tag_name> is given as string and represent the value of name attribute of the referred tag. We used this function to retrieve all Input tags:

var bone_stage = document.all.tags("INPUT");

when we obtain a collection with 154 objects for the document http://academicdirect.ro/virtual_library/TW2/index.html which implement the bone age evaluation.

The properties of HTML objects can be reads or writes on the same way. For example, for us are very important to retrieve the sex of the patient from sex drop down list:

patient_sex = document.all.sex.value;

The state of radio buttons from one bone (only one is checked) is obtained with:

if ( bone_stage(j).checked ) {

…

}

With helps of the java script operators, the programming can be easily made. Operators take one or more variables or values (operands) and return a new value; e.g. the ‘/’ operators can divide two numbers to produce a new one. We use operators in expressions to relate values, whether to perform arithmetic or compare quantities. JavaScript operators are based on C++ one. Thus, JavaScript provides a number of operators divided into several classes depending on the relationship they perform [8]. The classification of these operators is given in table 4-7. Arithmetic operators take numerical values or their operands and return a single value. The standard arithmetic operators are given in table 5. A comparison operator compares its operands and returns a logical value based on whether the comparison is true or false. The operands can be numerical or string values. When used on string values, the comparisons are based on the alphabetic ordering (table 6). Boolean operators are used to combine multiple comparisons into a conditional expression. Boolean operators work with two operands, each of which is a true or false value, and return a true or false result (table 7). The assignment operator (=) lets us assign a value to a variable. We can assign any value to a variable, included another variable (table 8).

Table 5. Arithmetic or computational operators

+ (plus sign)	Addition
- (minus sign)	Subtraction
* (asterisk)	Multiplication
/ (forward slash)	Division
% (percent sign)	Modulus: the remainder after division
++ (increment)	This operator takes only one operand. The operand’s is increased by 1. The value returned depends on whether the ++ operator is placed before or after the operand. E.g. ++y will return the value of y following the increment where as y++ will return the value of y prior to the decrement.
-- (decrement)	This operator takes only one operand. The operand’s value is decreased by 1. The value returned depends, as in the case of unary increment, on whether the -- operator is placed before or after the operand. E.g. --y will return the value of y following the decrement whereas y-- will return the value of y prior to the decrement.
-	Unary negation: returns the negation of operands.

Table 6. Comparison operators

== (equal to)	Returns true if operands are equal.
!= (not equal to)	Returns true if operands are not equal.
> (greater than)	Returns true if left operand is greater than right one.
>= (greater than or equal to)	Returns true if left operands is greater than or equal to right operand.
< (less than)	Returns true if left operand is less than right operand.
<= (less than or equal to)	Returns true if left operand is less than or equal to right operand.

Table 7. Boolean operators

&& (and)	Returns true if both operands are true.
\|\| (or)	Returns true if either operand is true.
! (not)	Returns true if the negation of the operand is true (e. g. the operand is false).

Table 8. Assignment operators

Assigns the value of the right hand operand to the variable on the left.

(also -= , *= , /=)

Adds the value of the right hand operand to the left hand variable and stores the result in the left hand variable.

&= (also !=)

Assigns result of (left hand operand && right hand operand) to left hand operand.

JavaScript functions are more like biological functions. It cumulates or multiplies using some algorithm a set of values to give a specific response to the main program. A function is composed from a set of statements, which perform some action. It may accept incoming values (parameters), and it may return an outgoing value. To create a function it is necessary to define its name, any values or arguments and some statements:

function <function_name>(argument1, argument2, …) { <statements> };

We can create a function without arguments (like procedures in Pascal) but in this case, the function must include the parentheses, as in the example below:

function <functionName>() { <statements> };

We used this kind of function in our program to the beginning of the program in order to compute the maturity score and bone age on base of individual bone:

function bone_stage_calculation() {

var individual_bone_maturity_score = new Array(new Array(new

Array(2), new Array(2), …), …);

//20 new Array of 9 new Array(2) inside of new Array

…

individual_bone_maturity_score [14][6][0] = 92;

individual_bone_maturity_score [14][6][1] = 97;

…

for (i = 0; i < 1; i++) {

da = 0;

for (j = k; j < k+8; j++)

if ( bone_stage(j).checked ){

if (document.all.Sex.value == 'M') b +=

individual_bone_maturity_score[i][j-k][0];

else b += individual_bone_maturity_score[i][j-k][1];

da = 1;

}

k += 8;

if (da > 0) colect += bone_name[i]+', ';

}

…

};

As we used in bone_stage_calculation function, there exist a simple way to output the values to the screen. The write function of the document object makes this very easy:

...

document.write(colect);

...

where colect is a string variable that contain the string for output. Also the document.write function can be used to display a constant string:

document.write("Tanner-Whitehouse Test");

Some interactive I/O functions are also available: alert, prompt and confirm. These functions are generally used for advertising or for submitting data to the server, but are very useful for program debugging and developing. We used the alert function to display number of INPUT tags from the document in testing phase:

alert(document.all.tags("INPUT").length) ; // display 154

Dynamically Building of a HTML Page

In order to create a dynamically program and interactive one we used some statements. Statements define the flow of a script, known as program flow. A statement is made up of small expressions, which evaluate into a cogent meaning. Form JavaScript statements we used in our program a loops statement (for), and a conditional statement (if ...else) [8]. for loop repeatedly cycles though a block of statements until a test condition is false. This statement is used commonly to initialize a counter variable. The number of times a loop is repeated depends on a counter. The JavaScript for syntax incorporates the counter and its increments, as below:

for (<initial_statements>; <evaluate_conditions>; <end_statements>) {<statements>}

if (<conditional_statement>) <statement1>; [ else <statement2>;]

where initial statements are made only at beginning of the cycle, are separately by ",”.

We used in our program the next sequence of three for’s:

for (i = 0; i < 1; i++){

document.write("<BR><hr size='5' color='#191970'

width='40%'><h2><font color='#800000'>" +

bone_name[i]+"</h2></font><table border='1'>");

for (j = 1; j < 9; j++){

document.write("<tr><td><input type='radio' id='x"+i+"_"+j+

"' name='o"+i+"' value='"+j+"'>");

for (k = 1; k < 4;k++){

document.write("<td align='center'><img src='"+i+"_"+j+"_"+

k+".jpg' height='100'>");

}

document.write("<td>"+standard_bone_stage[i][j]+"<BR>");

}

document.write("</table>");

}

A set of form type objects (input, select, …) for patient information may be used in order to send the data to a web server or compute directly in java script program. The purpose of this program is to allow computer assessment of child bone age in order to compare the result with biological age. Because the Tanner-Whitehouse method used to assess the skeletal maturity has some results for boys and other results for girls first we create using document.write a sub-table which allows us to choose child sex (see the example below). We present now how we create the sex sub-table using form controls:

document.write("<BR><hr size='7' color='#191970'><BR>");

document.write("<center><table width='50%' border=1><tr>");

document.write("<td>Sex:<BR><select name='sex'>");

document.write("<option value='M' selected>Male</option>");

document.write("<option value='F'>Female</option></select>");

In order to create a database with all the bone ages assess with this program we created a form with the patient data:

document.write("<form method=post"+"action='eval.php'>");

Evaluation Function

The present paper describes the assessment of child skeletal maturity based on JavaScript programming language. In order to assess the child bone age, first, the program took in consideration all the individual score bone on the based of what the radiologist checked:

for (i = 0; i < 1; i++){

da = 0;

for (j = k; j < k+8; j++)

if ( bone_stage(j).checked ){

if (document.all.Sex.value=='M') b+=

individual_bone_maturity_score[i][j-k][0];

else b += individual_bone_maturity_score[i][j-k][1];

da = 1;

}

k += 8;

if (da>0) colect += bone_name[i]+', ';

}

At the end, the bone_stage_calculation() function sum all the individual bone stage score, and assign for every maturity score, differentiate on sex, a bone age:

if (document.all.Sex.value == 'M'){

var boys_maturity_score = new Array(171);

boys_maturity_score[0]=114;

boys_maturity_score[1]=116;

...

if (b>0) for(k = 0; k<171; k++) {

if (boys_maturity_score[k]>=b) {

colect += "<tr><td>Maturity score:<td>"+b+" ->

"+boys_maturity_score[k]+"<tr><td>Bone age:<td>"+(1+k/10);

break;

}

} else colect +=

"<tr><td>Maturity score:<td>0 -> 0<tr><td>Bone age:<td>0";

} else {

var girls_maturity_score=new Array (151);

girls_maturity_score[0]=131;

girls_maturity_score[1]=136;

if (b>0) for(k = 0; k<150; k++) {

if (girls_maturity_score[k] >= b) {

colect +="<tr><td>Maturity score:<td>"+b+" -> "+

girls_maturity_score[k]+"<tr><td>Bone age:<td>"+(1+k/10);

break;

}

} else colect +=

"<tr><td>Maturity score:<td>0 -> 0<tr><td>Bone age:<td>0";

}

Results

Our software integrates the Tanner-Whitehouse method in a fact and reliable way. It is easy to use, have a friendly interface (see figure 4) and reduce the time needed to obtain final bone age from 8-10 minutes to 3-5 minutes.

It is a PC’s program and it is quite easy to run in any computer. The minimum required for running the program is an HTML 4.0 web browser (like Internet Explorer 4.0, Netscape 4.7, Mozzilla, Opera, and so on). With this minimum requirement, the program is quite easy to install it in a clinical environment.

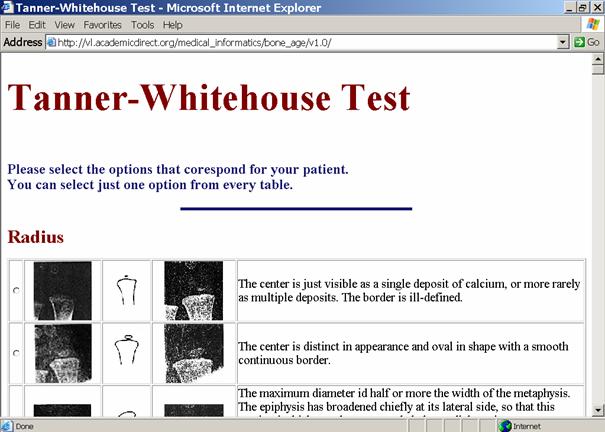
Fig. 4. Java script program running (index.html)

The program subsumes all the documentation of Tanners-Whitehouse atlas, including the standardized image. They are available on the screen when the radiologists use the program.

For every bone from 20^th, the radiologists choose, whit a mouse click, the patient individual bone maturity stage. For one bone, the program allows choosing just a single maturity stage. To every bone, maturity stage was assign, on based of Tanner-Whitehouse standard, a score.

The program allows users to input some specific data such as: the patient personal number, the first and second name of the patient, the patient address, the patient chronological age, the patient weight and height, the patient diagnosis, the date of patient examination (figure 5).

In order to use our program it is necessary to follow three steps, represented by:

· choosing the bone maturity stage, for every bone;

· introducing the patient data;

· displaying the Tanner-Whitehouse test results.

Fig. 5. Input patient data interface (these data are fictive one)

At the end, the program creates a report (figure 6) with all the patient data, and displays the skeletal maturity score and corresponding bone age. The report can be print or can be save on the computer hard disk or on a floppy disk.

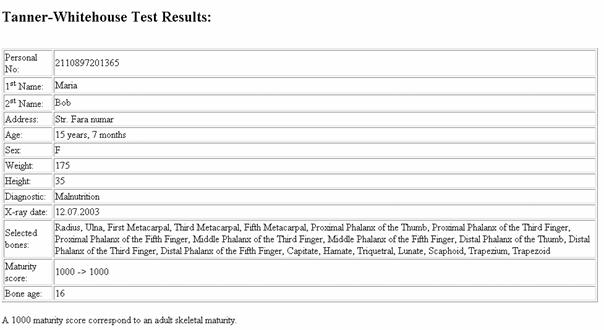
Fig. 6. Patient report (the data from this report do not belong to any patient).

The performance of the computerized procedure depends to some extend on the interaction user and on the familiarization of the radiologists with a Web browser. On the other hand, the program performance also depends on the radiologist’s experiences, experience which is essential.

However, the execution time of the total process of bone age assessment is always significantly shorter than the time necessary for the traditionally subjective visual rating.

Discussions

Why is so important to assess skeletal maturity? Is quite simple, the development and growth of children is a very important issue for every country. It is important to have healthy children because if we have healthy children now, in the feature, will we have healthy adults.

Radiographs of the hand and wrist, which representing well al the skeletal system, has been used in order to assess bone age for the following reasons:

· it is easy to take a left hand and wrist radiograph;

· the development of the hand and wrist is not different from that of other bones such as knee, foot or pelvis;

· the accuracy of an analysis of skeletal maturity of the hand and wrist is not inferior to that of many other bones;

· the ossification of the carpal bones not only appears uniformly in order but also is affected more by illness or inadequate nutritional conditions rather than genetic factors [9],[10].

The Tanner-Whitehouse system (TW2) was made by Tanner-Whitehouse in 1972 by a longitudinal and cross sectional study. The size, shape, density, smoothness or thickening of the borders, thickness of epiphyseal line, extent of fusion and capping of the twenty bones of the left hand (distal radius; distal ulna; first, third and fifth metacarpals; proximal phalanges of the thumb, third and fifth fingers; middle phalanges of the third and fifth fingers; distal phalanges of the thumb, third and fifth fingers; the seventh carpal bones: capitate, hamate, triquetral, lunate, scaphoid, trapezium and trapezoid) were analyzed and graded into 8 or 9 stages from A to H or I according to the degree of maturity and scored from 0 to 1000 according to the biological weight which indicate the bone maturity by stages [4].

Our program subsumes all the documentation of Tanners-Whitehouse atlas, including the standardized image. They are available on the screen when the radiologists use the program. The program is easy to use and it is an important tool in pediatric radiology.

The program can be extended in order to compute RUS bone maturity score – this score use just radius, ulna and finger bones, and/or Carpal bone maturity score – use only carpal bones. Can also be developing an automated system of bone age maturity evaluation applied on the base of the Tanner-Whitehouse method.

The program can be improved to send the resulted data to a Web server. This task can be easily done using a PHP program [11] in order to create a large database (in this case usually a MySQL database [12]) with patients results. The database can be after that interrogates to retrieve the data results for selected patient, to make computation on groups of patients, in order to relieve group dependencies.

Conclusions

We presented a helpful program in skeletal maturity assessment that includes the Tanner-Whitehouse method. Now, radiological department have at their disposition an efficient and useful program in assessing the child skeletal maturity. The program have a nicely interface, is easy to use and significantly reduces the time need to obtain final bone age, from 8-10 minutes to 3-5 minutes.

The program which was dynamically create allow interaction with the users and can run from any computer, if on computer is installed Internet Explorer 4.0. It is quite easy to install the program in a clinical environment. The program is a powerful tool for routine application in pediatric radiology.

References