Modelling and Simulation of Crude Oil Dispersion
Abdulfatai Jimoh and Mohammed Alhassan
Department of Chemical Engineering, Federal University of Technology, Minna, Nigeria,
Abstract
This research work was carried out to develop a model equation for the dispersion of crude oil in water. Seven different crude oils (Bonny Light, Antan Terminal, Bonny Medium, Qua Iboe Light, Brass Light Mbede, Forcados Blend and Heavy H) were used as the subject crude oils. The developed model equation in this project which is given as:
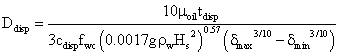
It was developed starting from the equation for the oil dispersion rate in water which is given as:
![]()
The developed equation was then simulated with the aid of MathCAD 2000 Professional software. The experimental and model results obtained from the simulation of the model equation were plotted on the same axis against time of dispersion. The model results revealed close fittings between the experimental and the model results because the correlation coefficients and the r-square values calculated using Spreadsheet Program were both found to be unity (1.00).
Keywords
Dispersion; Simulation; Crude oil
Introduction
Crude oil is naturally occurring oil, bituminous liquid composed predominantly of various organic chemicals. It is found in large quantities below the surface of earth and is used as a fuel and as a raw material in the chemical industries [1].
The Fumes are putrid; respiration is impaired; the local says they cannot fish on river; they can neither farm as their land has being devastated (The Guardian, Tuesday August 20, 2002, Debo Adesina, Oil spill in Niger Delta area, Guardian News papers limited, Lagos, p. 1-20). Such is the story of communities in the Niger delta region of Nigeria.
Of all the different ways in which the industrialized world's use of energy can damage the natural environment, the most vivid for many people may be oil spills. On a seemingly regular basis, our newspapers and television screens are filled with pictures of listing tankers spilling crude oil (also known as petroleum), and oil soaked sea-birds in various stages of death. While these oil spills may be the most publicized (the Exxon Valdez for example), accidental spills from tankers account for only about 20% of the crude oil discharged into the world's oceans each year. The remaining 80% is largely a result of routine oil tanker operations such as emptying ballast tanks. There are possible methods of reducing the amount of crude oil released into our oceans each year, but as long as vast amounts of oil are routinely transported by sea, there will be some amount of unavoidable spillage [2] over the year. The people have had their aquatic environment polluted as a result of oil spillage that refuses to dry up after many years of occurrence.
Oil spills vary widely in magnitude, location, and in the degree of soil, debris and water contamination. In addition to accidental spills, oily waters are encountered in the production of petroleum (produced water), in numerous waste pits, and in manufacturing operations involving lubricating oils [3]. Although each situation calls for a special set of remediation operations, it is useful to develop a generalized approach that can be adapted to specific conditions. This generalized approach can be visualized in terms of a mathematical model.
There is frequent dispersion of crude in the Niger-Delta Area. These dispersions have really become the topic of the day in the Niger-Delta Area owing to the resulting harm from this problem. On completion of this work, the time it would take certain quantity of crude oil dispersed to reach a particular distance could be predicted. As a corollary, the distance that a particular crude dispersion will reach at a given time will also be predicted using a model equation. The model developed can be simulated with the aid of a computer soft ware called MathCad 2000 professional in addition to spread sheet programmed to analyze the result for its validity. This can then be used for the control of dispersion of crude oil in the concerned areas.
This project is therefore a contribution towards the sustainability of the environment of the Niger-Delta Area as the model developed can be used to effectively monitor and predict the extent of movement of the spilled oil. This will enhance oils remediation measure to be put in place.
Literature Review
Crude oil or petroleum (derived from Latin petrus-rock and oleum-oil) or mineral oil is a thick, dark brown or greenish flammable liquid, which, at certain points, exists in the upper strata of Earth's crust. It consists of a complex mixture of various hydrocarbons, largely of the methane series, but may vary much in appearance, composition, and Crude oil properties. It can be shortened to the prefix petro-, as in "petrodiesel" [1].
Oil Spill
An oil spill is the release of crude oil into the natural environment, usually the ocean. An oil spill that occurs near a coastline will always impact more living organisms then one which occurs in the open ocean. This is simply because coastal areas are home to much more concentrated and diversified populations of marine life than the open ocean. Nevertheless, all oil spills have an impact on marine organisms, and oil from open ocean spills can end up contaminating beaches hundreds of miles away. Oil spills can harm marine life in three different ways, by poisoning after ingestion, by direct contact and by destroying habitats [2].
Causes of oil spills
Crude oil spills may be caused by:
· Mistakes or carelessness from people;
· Break down of equipment;
· Natural disasters such as hurricanes;
· Deliberate acts by terrorists, countries at war, vandals, or illegal dumpers [4].
As a corollary, the distance that a particular crude dispersion will reach at a given time can be predicted by developing a model equation and the model developed can be simulated with the aid of a computer soft ware called MathCad 2000 professional in addition to spread sheet programmed to analyze the result for its validity. This can then be used for the control of dispersion of crude oil in the concerned areas.
CAD Procedure
MathCAD is a rich problem-solving environment that gives a wide choice of tools and supports a variety of analysis and visualization techniques. MathCAD is now being used by hundreds of thousands of engineers, scientists, and students across a broad range of technical disciplines. To give a flavour for some applications, it has an assembled library of application files demonstrating how MathCAD is being used to solve problems in various engineering fields.
In the most general sense, MathCAD can be thought of as a combination of
· a powerful technical computing environment cantered on real math notation, and
· a flexible, full-featured technical word processor.
Unlike other technical software, MathCAD performs mathematics the same way one does. That’s because it looks and works like a pad of paper and pencil. MathCAD’s on-screen interface is a blank worksheet on which one enters equations, graph data or functions, and annotates with text - anywhere on the page. Mathematical expressions in MathCAD look the way one would see them in a text or a reference. The only difference is that MathCAD’s equations and graphs are “live.” Changing any data, variable or equation makes MathCAD to recalculate the worksheet - instantly.
This underlying technology is referred to as MathCAD’s “Live Document Interface”. Spreadsheet software has achieved great popularity because of its availability for microcomputers at reasonable cost, the ease of learning and using the software, and its flexible application to many problems. Solutions for many engineering problems can be achieved rapidly by spreadsheet than by writing a language code program, such as FORTRAN or BASIC. The term “spreadsheet” refers to row and column organizational form of the input and output of the software [5].
Mathematical modelling is a comprehensive process of representing real-world phenomena in terms of mathematical equations and extracting from them useful information for understanding and prediction. In the process of idealization, some simplifications will have been made in obtaining the mathematical model. Therefore, the mathematical model is less real than the system is supposed to represent. Nevertheless, it is an essential step in the construction of a theory. To quote Boltzmann, there is nothing as practical as a good theory ([6] and [7]).
Developing a mathematical model is a long and arduous task. In mathematical modelling, the goal of the modeller is to ensure that the model replicates the phenomena being modelled to an acceptable degree.
The procedures followed to test the fidelity of the model in reproducing the real system it represents constitute model validation. On the surface, it appears that validation is something that should be done at the end of the model construction. But, in fact, validation should be carried out throughout the modelling process.
A valid model can be expected by being logically consistent at each step of the modelling process by re-examining the assumptions and constraints without sacrificing the mathematical rigour, and by running every stone of applicable mathematical knowledge [6]. The advances in high-speed computers and efficient numerical algorithms have generated acceptable numerical solutions to systems of the equations hitherto intractable and thus made modelling of complicated, interconnected, and interacting systems possible.
Methodology
Experimental Procedure and Apparatus
The experimental analysis was based on the spread of samples of Nigeria crude oil on water surface. Apparatus: water channel, raw petroleum sample, measuring tape, stop watch, thermometer-measuring cylinder etc.
Determination of dispersion of crude oils
The experimental apparatus consist of a water channel of length 3m and width of 0.25m as well as the water depth of 0.4m. First and foremost, prior to the experiment, the channel was first cleaned and flushed out with tap water to ensure cleaning of the channel surface.
After then, the channel was filled with water and left to calm down to become stagnant. Furthermore, the channel was divided into twenty (20) parts of 150 cm each; each division was marked with a coloured material. A predetermined quantity of Nigeria crude oil sample at different volume of 30cm3, 35cm3, 30cm3, 40cm3, 45cm3, 50cm3 and 55cm3 that was collected from Shell, Agip and Elf oil well was released at one end of the channel and allowed to spread over the water surface. The time of dispersion was noted starting instantly at the time the oil was released into the water.
Modelling and Simulation Methodology
The model proposed is based on the work [8]. The model developed was simulated with the aid of computer software called MathCAD 2000 Professional. In addition, Spreadsheet Program was used to analyze the results to determine their conformities with the experimental results and the results were presented in figure 1 to 7.
For modelling of oil dispersion in water the basis of this modelling is chosen to be the work [8]. For this model, the entrainment of oil is estimated and the equation obtained was used as the basis equation for the development of the distance of dispersion as a function of time. In developing this model for oil dispersion in water, the following assumptions were made:
· Dispersion is considered to take place in the direction of flow of current of water;
· Maximum droplet size is set equal with droplet size that would not be expected to re float;
· The surface of the stream of water is considered to be placid;
· Effect of temperature and pressure are neglected;
· Effect of wind is also neglected.
Model expression
Starting from the equation derived by Delvigne and Sweeney [8], the oil dispersion rate in water is given as:
Qdisp = cdispÃe0.57fbwfdisp (1)
where cdisp is the empirical dispersion constant, Ãe is the dissipation of wave energy per unit area (J/m2), fbw is the fraction of breaking wave of water per second (s-1), fdisp is the volume of oil entrained per unit water volume.
Further, the dissipation of wave energy per unit area, Ãe, is given as:
Ãe = 0.0017gρwHs2 (2)
where g is the gravitational acceleration (m/s2), rw is the density of water, Hs is the significant wave height (m).
The fraction of breaking wave of water per second, fbw, is given as:
fbw = fwc/tp (3)
where fwc is the fraction of water surface covered by oil and tp is the time of dispersion. Given that d is the oil droplet diameter, the relationship between the volume of oil entrained per unit water volume, fdisp, and the oil droplet diameter, d, can be expressed as:
fdisp ≈ ![]() (4)
(4)
where N(d) is the droplet number per unit volume of water per unit droplet diameter and it is given as:
N(δ) ≈ δ-2/3 (5)
Substituting equation (5) into equation (4), and integrating, we have:
fdisp = (δmax10/3 – δmin10/3)∙3/10 (6)
Equation (1) becomes, after substituting the expressions of Ãe, fbw and fdisp:
Qdisp = 3cdispfwc(0.017gρwHs2)0.57(δmax10/3 – δmin10/3)/(10tp) (7)
Using dimensional analysis, the ratio of the viscosity of the oil to the oil dispersion rate is equal to the distance of dispersion. That is:
<μoil> [kgm-1s-1]/<Qdisp> [kgm-2s-1] = <Ddisp> [m] (8)
where moil is the viscosity of the oil, Qdisp is the dispersion rate, and Ddisp is the distance of dispersion of the oil.
So,
Ddisp = 10μoiltp/(3cdisp∙(0.0017gρwHs2)0.57fwc[δmax10/3-δmin10/3]) (9)
Denote tp as tdisp. That is, making tdisp = tp:
Ddisp = 10μoiltdisp/(3cdisp∙(0.0017gρwHs2)0.57fwc[δmax10/3-δmin10/3]) (10)
Equation 10 is, thus, the model equation for the dispersion of crude oil in water. The equation shows the distance of dispersion as a function of time of dispersion.
Results
The experimental results are in figures 1 to 7.
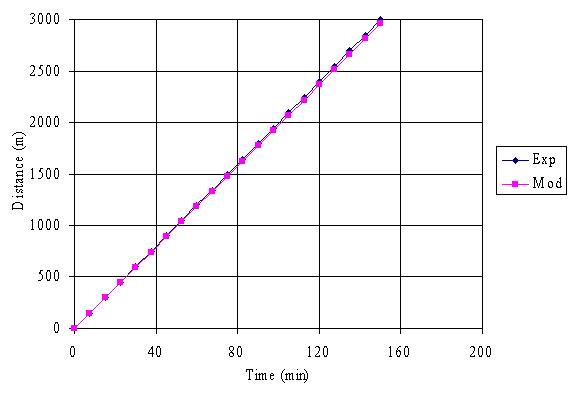
Fig. 1. Graph of experimental and model distances versus time for Bonny Light
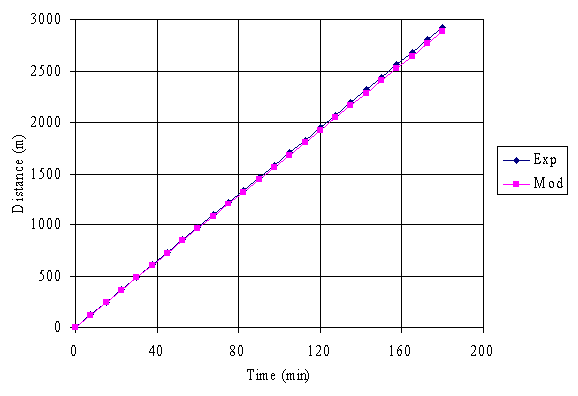
Fig. 2. Graph of experimental and model distances versus time for Antan Terminal
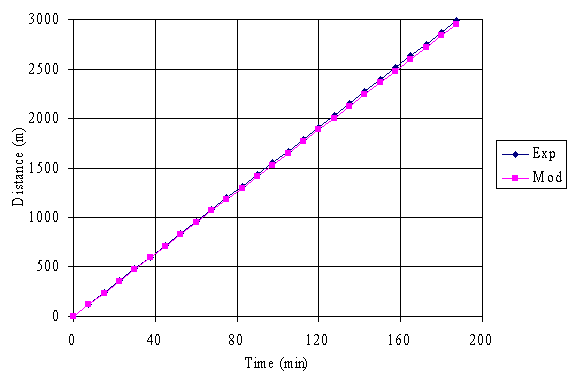
Fig. 3. Graph of experimental and model distances versus time for Bonny Medium
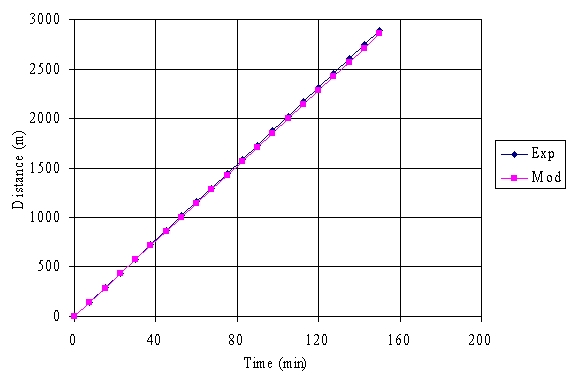
Fig. 4. Graph of experimental and model distances versus time for Qua Iboe Light
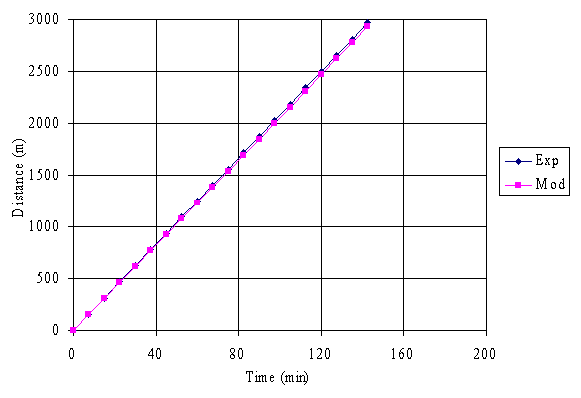
Fig. 5. Graph of experimental and model distances versus time for Brass Light

Fig. 6. Graph of experimental and model distances versus time for Forcados Blend
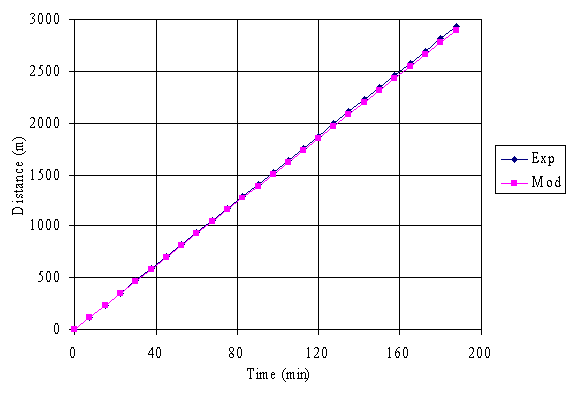
Fig. 7. Graph of experimental and model distances versus time for Heavy H
Discussions
The model equation obtained in this research work is as shown in Equation 21. It represents the distance of dispersion as a function of time.
The experimental and the model distances of dispersion were both plotted against time of dispersion on the same graph for the different samples of crude oil
It is obvious from figure 1 to 7 that the distance travelled by the crude oil increased as the time increases signifying that the distance of dispersion of the crude oil are proportional to the time of dispersion.
Comparison of the experimental and model results shows that there are reasonable levels of agreements between them, and the validity of the model equation was verified by calculating the correlation coefficients and r-square values using the Spreadsheet Program which were found to be 1.00 in each case for each of the crude oil sample considered. The unit values show how well the model equation represents the crude oil dispersion phenomenon, with respect to distance and time.
Conclusions
A model equation which represents the dispersion of crude oil in terms of distance and time has been developed, and simulated with the aid of computer software known as MathCAD 2000 Professional. The correlation coefficient and r-square values between the experimental and model values for each the oil sample were calculated using Spreadsheet Program and were both found to be unity (that is, 1.00). This shows how well the model equation represents the dispersion of crude oil in water with respect to distance and time.
References
[1] Perry R. H., and Green D. W., Perry’s Chemical Engineer’s Handbook, 6th Edition, McGraw Hill, New York, USA, p. 1-7, 1984.
[2] Energy Educators, Energy education resources, p. 1-50, 1993, accessed Oct 2002, http://eia.doe.gov/bookshelf/eer/kiddietoc.html.
[3] Anderson M. A., Rubin A. J., Adsorption of Inorganic at solid-liquid interfaces, Ann Arbor Science, Michigan, USA, p. 295-297, 1981.
[4] Brain Dicks, The environmental effects of Marine oil spils effect, Recovery and compensation, International Seminar on Tanker safety pollution, spill response and compensation, November 6, 1998, Rio de Janeiro, Brazil, p. 1-8, 1998.
[5] Peter, M. S. and Timmerhaus, K. D., Plant Design and Economic for Chemical Engineers, 4th Ed., McGraw Hill, New York, USA, p. 112-113, 1991.
[6] Xavier Avula J. R., Mathematical Modelling, University of Missouri-Rolla, Miner Circle,- Rolla, Missouri, USA, p. 107-119.
[7] Koutitas C. G., Mathematical Models in Coastal Engineering, Wiley Publishers, New Delhi, p. 49, 1988.
[8] Delvigne G. A. L., Sweeney C. E., Natural Dispersion of oil, Oil and Chemical Pollution, 4(4), p. 281-310, 1988.