Implementation of the Extended Conjugate Gradient Method for the Two-Dimensional Energized Wave Equation
Victor Onomza WAZIRI1*, Sunday Augustus REJU2
1Mathematics/Computer Science Department, Federal University of Technology, Minna 920003, Niger State, Nigeria; *corresponding author
2National Open University of Nigeria, Victoria Island, Lagos, Nigeria
dronomzawaziri@yahoo.com, sreju@nou.edu.ng
Abstract
The paper computes the optimal control and state of the two-dimensional Energized wave equation using the Extended Conjugate gradient Method (ECGM). This piece of work has to do with all the vital computational elements as derived in the implementation of the ECGM algorithm on the two-dimensional Energized Wave equation in (Waziri, 1) and (Waziri & Reju, LEJPT & LJS, Issues 9, 2006, [7-9]). With these recalls, program codes were derived which gave various numerical optimal controls and states. These optimal controls and states were considered at various points in a plane surface.
Keywords
Extended Conjugate Gradient Method (ECGM), Conjugate Gradient Method (CGM), Control operator and penalty cost
Introduction
The ECGM implementation algorithm for the two-dimensional energized wave problem is a modified pattern of the CGM algorithm by (Hestenes and Stiefel, 5). The optimal solutions of the energized wave equation are obtainable by substituting the control operator from (Waziri et al. 7), the analytical solution from (Waziri et al., 8) and the penalty functional elements from (Waziri et al. 9) into the CGM implementation frameworks models.
The implementation of the ECGM algorithm
In this optimization computational problem for the two-dimensional energized equation, the details are in line with CGM framework algorithm developed by (Hestenes et al. ibid). Since this is a computer based algorithm, the initialization is based on the default of the computer. The outline details for the implementation runs sequentially in this order:
![]() 1
1
![]() 2
2
Equations 1 and 2 clearly define the templates for the construction of
the optimal state and control respectively. The ![]() appearing are the step lengths
that speed up the rate of convergence, while the
appearing are the step lengths
that speed up the rate of convergence, while the ![]() and
and ![]() denote the conjugate directions
for the state and controls respectively. The step lengths for the state and
control are uniquely defined in these orders:
denote the conjugate directions
for the state and controls respectively. The step lengths for the state and
control are uniquely defined in these orders:
![]() 3
3
![]() 4
4
The penalized descent direction step lengths are similarly uniquely defined as:
![]() 5
5
![]() 6
6
The ![]() simply
symbolize the penalized descent direction s with respect to the control and
state.
simply
symbolize the penalized descent direction s with respect to the control and
state.
The gradients of the state and control for the ![]() terms are symbolically
given as:
terms are symbolically
given as:
![]() 7
7
![]() 8
8
The![]() iterative descent algorithm for the state and control are:
iterative descent algorithm for the state and control are:
![]() 9
9
![]() 10
10
To make effective computational manipulation of the CGM algorithm as portrayed in equations 1 through 10 to our problem, we must derive some of the elements of the model. Thus consider our unconstrained problem for the two-dimensional energized wave equation from (Waziri 2006a) reproduced hereunder for convenience:
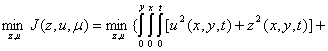
![]()
![]() 11
11
From now onward, the unconstraint equation 11 shall be referred to as J(z, u, μ) symbolically, its gradients in the control pattern are:
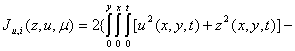
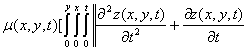
![]() 12
12
The gradient with respect to the state trajectory:
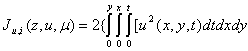 13
13
The penalized descent direction p(x, y, t) in the control and state are defined as follows:
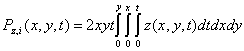 14
14
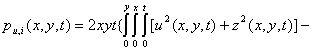
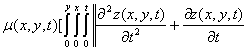
![]() 15
15
Now the product of the control operator and the descent direction ![]() are
analytically derived from the control operator in (Waziri et al., 7).
are
analytically derived from the control operator in (Waziri et al., 7).
![]()
![]()
![]()
![]()
![]()
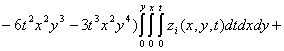
![]()
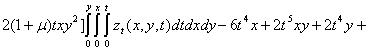
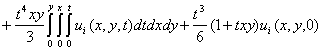
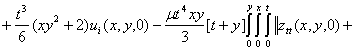
![]() 16
16
The descent penalized product with the control operator is
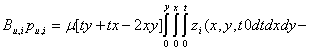
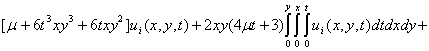
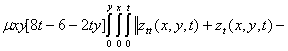
![]() 17
17
The derivations of 16 and 17 were successful after much algebraic manipulations from the control operator in (Waziri et al., 7). In furtherance of the implementation of the ECGM algorithm based on the problem at hand (the energized wave equation), these derivation as acquired from (Waziri et al. 7 and 8) are worthy of note:
![]()
![]()
![]()
![]() 18
18
![]()
![]()
![]()
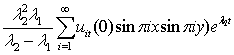 19
19
![]()
![]()
![]()
![]() 20
20
![]()
![]() 21
21
![]()
![]()
![]() 22
22
with t = 0, the following initial conditions are not difficult to obtain from equations 18 through to 22:
![]()
![]() 23
23
![]()
![]() 24
24
![]()
![]() 25
25
![]()
![]() 26
26
Substituting the derivations of equations 18 through to 22 into equations 16 and 17, the products of the descent directions and the control operator can be obtained. The penalty functional because of its role in the ECGM is hereby recalled from (Waziri et al., 9):
![]()
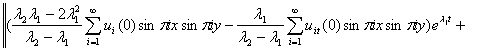

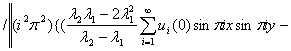
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
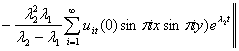 27
27
Haven derived all the necessary elements for the ECGM implementation algorithm; program codes are written after all the necessary substitutional processes into the CGM algorithmic pattern.
The optimal control and state outputs
We make the following observations in summarized tabular form under various
observations of the initial amplitudes and velocity at distinct plane profiles in
supposedly abstractive spatial planes with tolerance ![]() by the application of
program codes.
by the application of
program codes.
Tables 1 and 2 respectively give the general summary of the optimal controls and states. Each optimal state or control is a minimum value from large data of numerical iterates.
The optimal controls at different chosen plane profiles are:
Table 1. The optimal control outputs
|
Profile |
Optimal control
|
|
2 |
6.527768358707·10-3 |
|
20 |
8.628852613291·10-6 |
|
30 |
5.2435629541742·10-6 |
|
40 |
5.2493559230290·10-6 |
|
50 |
2.3778749100400·10-6 |
|
60 |
1.9370795580080·10-6 |
|
70 |
1.9370315046425·10-6 |
|
80 |
1.9369967833300·10-6 |
The optimal states spatial plane values at various plane profiles are given in table 2:
Table2. The optimal control outputs
|
n-strata |
Optimal State-z(x,y,t) |
|
2 |
4.9016613961·10-3 |
|
20 |
1.9915249395·10-5 |
|
30 |
1.1301179301·10-6 |
|
40 |
1.1301428582·10-6 |
|
50 |
9.9019978309·10-6 |
|
60 |
6.5247634064·10-8 |
|
70 |
6.5248045988·10-6 |
|
80 |
6.5248354507·10-6 |
Conclusion
We observe that as the strata profiles in space increase from n = 2 and n = 20, the optimal state values are relatively stable with just a negligible local error. Between n = 30 and n = 40, the optimal state and control maintain stability at n = 50 there is a slight jump in values for the state but a decrease in the control. After these points, the optimal state and control values at n = 60 and n = 80 remain stable.
References
[1] Hestenes M. R., Stiefel E., Method of conjugate Gradient Method for solving linear systems, Journal of Research of the National Bureau of Standards; 49, 1952, p. 409-436,.
[2] Ibiejugba M. A., Onumanyi P., On Control Operator and some of its Applications, J. Math. Analy. and Applic., 103, 1984, p. 31-37,.
[3] Omolehin J. O., On control of reaction Diffusion, Ph.D. Thesis, University of Ilorin, Nigeria, 1991.
[4] Reju S. A., Computational Optimization in Mathematical physics; Ph.D. Thesis, University of Ilorin, Ilorin, Nigeria, 1995.
[5] Hestenes M. A., Stiefel, Method of Conjugate Gradients for solving linear systems. J. Res NBS, 320, 1952.
[6] Waziri V. O., Optimal Control of Energized Wave equations using the Extended Conjugate Gradient Method (ECGM), Ph.D. Thesis, Federal University of Technology, Minna, Nigeria, 2004.
[7] Waziri V. O., Reju S. A., Control Operator for the Two-Dimensional Energized Wave Equation, Leonardo Journal of Science, ISSN 1583-0233, Issue 9, July-December, 2006, p. 33-41.
[8] Waziri V. O., Reju S. A., The Analysis of the Two-dimensional Diffusion Equation With a Source, Leonardo Journal of Science, ISSN 1583-1078, Issue 9, July-December, 2006, p.43-53.
[9] Waziri V. O., Reju S. A., The Penalty Cost Functional for the Two-dimensional Energized Wave Equation, Leonardo Journal of Science, ISSN 1583-0233, Issue 9, July-December, 2006, p. 45-52.