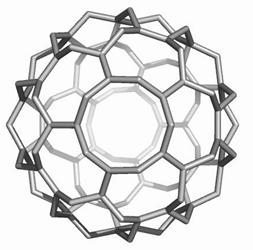
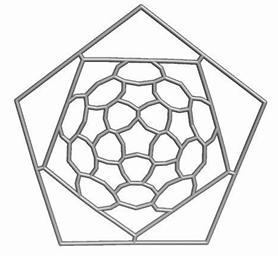
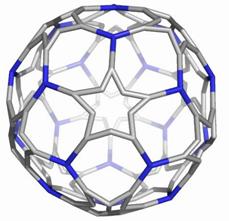
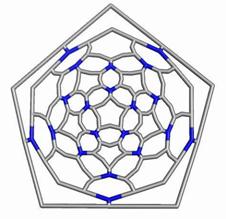
Fantasmagoric Fulleroids Revisited
Mircea V. DIUDEA
Faculty of Chemistry and Chemical Engineering,
“Babes-Bolyai” University, 400028, Cluj, Romania
Abstract
New strange fulleroids are built up by using the three classical composite map operations: tripling (leapfrog Le), quadrupling (chamfering Q) and septupling (capra Ca) on the starting structure dodecahedron. These transforms belong to the icosahedral symmetry group and show interesting mathematical and (possible) physico-chemical properties. Topological symmetry data of the presented cages are calculated by means of layer matrices derived on the associated graphs and their medial and dual transforms.
Keywords
Fulleroids, Composite operations on maps, Graphs
Introduction
A map M is a combinatorial representation of a closed surface [1]. Several transformations (i.e., operations) on maps are known and used for various purposes.
Let us denote in a map: v - number of vertices, e - number of edges, f - number of faces and d - vertex degree. A subscript “0” will mark the corresponding parameters in the parent map.
Recall some basic relations in a map [2]:
ådnd = 2e (1)
åsfs = 2e (2)
where vd and fs are the number of vertices of degree d and number of s-gonal faces, respectively. The two relations are joined in the famous Euler [3] formula:
ν – e + f = χ(M) = 2(1-g) (3)
with c being the Euler characteristic and g the genus [4] of a graph (i.e., the number of handles attached to the sphere to make it homeomorphic to the surface on which the given graph is embedded; g = 0 for a planar graph and 1 for a toroidal graph). Positive/negative c values indicate positive/negative curvature of a lattice. This formula is useful for checking the consistency of an assumed structure.
It is assumed that simple map operations, like dualization, stellation, truncation, medial, etc. are well-known; the reader is referred to some already published papers [5].
Composite Operations on Maps
Leapfrog Le is a composite operation [6]-[10] which can be written as:
Le(M) = Du(P3(M)) = Tr(Du(M)) (4)
A sequence of stellation (i.e., P3) - dualization rotates the parent s-gonal faces by p/s. Leapfrog operation is illustrated, for a tetragonal face, in Figure 1.
A bounding polygon, of size 2d0, is formed around each original vertex. In the most frequent cases of 4- and 3-valent maps, the bounding polygon is an octagon and a hexagon, respectively.
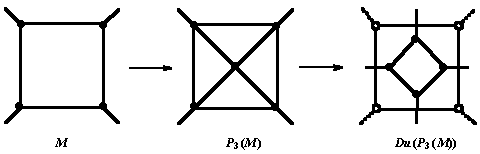
Figure 1. Le operation on a tetragonal face of a trivalent net
In trivalent maps, Le(M) is the tripling operation. The complete transformed parameters are:
Le(M): n = s0f0 = d0n0; e = 3e0; f = n0 + f0 (5)
Quadrupling Q (i.e., chamfering [11]) is another composite operation, achieved by the sequence [12]:
Q(M) = E_(TrP3(P3(M))) (6)
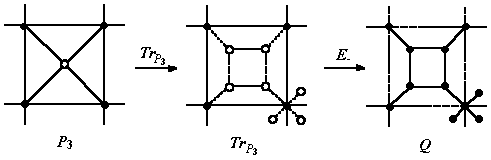
Figure 2. Q operation on a tetragonal face of a trivalent net
The complete transformed parameters are:
Q(M): n = (d0 + 1)n0; e = 4e0; f = f0 + e0 (7)
Q operation leaves unchanged the initial orientation of the polygonal faces. Note that, the quadrupling transform of a 4-valent map is not a regular graph anymore (because of mixing the new trivalent vertices with the parent 4-valent ones). Only Q(M) of a 3-valent map is a 3-regular graph.
Q insulates the parent faces always by hexagons.
capra Ca - the goat, is the romanian corresponding of the leapfrog English children game. It is a composite operation, 12 necessarily coming from the Goldberg’s 11 multiplying factor m:
M = (a2 + ab + b2); a ³ b; a + b > 0 (8)
that predicts m (in a 3-valent map) as follows: Le: (1, 1); m = 3; Q: (2, 0); m = 4; Ca: (2, 1); m = 7.
The transformation can be written as 12:
Ca(M) = TrP5(P5(M)) (9)
with TrP5 meaning the truncation of each vertex where P5 capping faces of a parent face are incident.
Ca insulates any face of M by its own hexagons, which are not shared with any old face (in contrast to Le or Q).
The operation is illustrated in Figure 3. Note that Ca is S1 operation which is different to S2 twin operation [13].
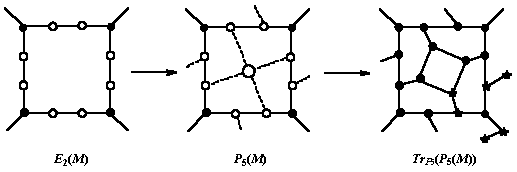
Figure 3. Ca operation on a tetragonal face of a trivalent lattice
Open Operation
The above operations Ω(M) can continue by an En homeomorphic transformation En(Ω(M)) of the boundary edges of the parent-like faces thus resulting open maps with all polygons of the same size. In case of E1 operation the size is: 9 (Le); 8 (Q) and 7 (Ca). This opening transformation is illustrated in Figures 4 to 6 in case of the dodecahedron D.
The opening faces by E1 operation are “zig-zag” tubule junctions. They can be further decorated by halves of the dodecahedron, thus entering pentagonal faces. Figures 7 to 9 illustrate the resulting objects, both in 3D and in 2D, as Schlegel projection [14].
|
E(Le(D))); v = 120 |
E(Le(D))); Schlegel projection |
|
|
|
Figure 4. Open of the Le(D)
|
E(Q(D))); v = 140 |
E(Q(D))); Schlegel projection |
|
|
|
Figure 5. Open of the Q(D)
|
E(Ca(D))); v = 200 |
E(Ca(D))); Schlegel projection |
|
|
|
Figure 6. Open of the Ca(D)
|
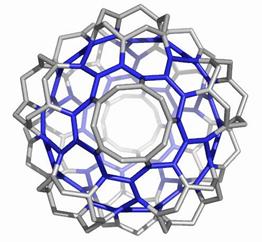
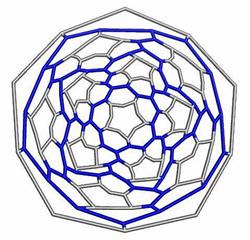
Dh(E(Le(D))); v = 180 |
|
|
|
|
Figure 7. The cage derived on Le(D) by opening the original faces and decorating by halves of D
|
Dh(E(Q(D))); v = 200 |
|
|
|
|
Figure 8. The cage derived on Q(D) by opening the original faces and decorating by halves of D
|
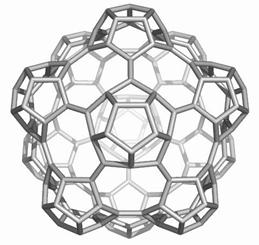
Dh(E(Ca(D))); v = 260 |
|
|
|
|
Figure 9. The cage derived on Ca(D) by opening the original faces and decorating by halves of D
Discussion
Given a graph G with S = S(G) being the set of subgraphs of a given size and a group of automorphisms Aut(G(S)), two subgraphs Si, Sj of G are called equivalent if there is a group element aut(NSi) Í Aut(G(S)) such that Sj aut(NSi) Si ( i.e., an automorphic permutation that transforms two subgraphs to each other).
The set of all subgraphs Sj obeying the above equivalence relation is called the orbit (i.e., class of equivalence) of the subgraph Si, SNSi. The orbits represent disjoint automorphic partitions: S = ÈSNSi. We limit here to find the equivalence classes for the vertices, edges and faces of these cages. As an equivalence criterion we used the index of centrality C(LM) defined on layer matrices LM [15]-[17].
The vertex orbits are found by applying the above index on the layer matrix of valences L1W of the parent graph. The edge orbits are calculable with the same index but applied on the corresponding medial graph.
The face orbits are obtained from the dual of the parent graph. Each vertex in the dual has the valence equal to the parent face size. In this way one can select the orbits for each face type. Topological symmetry data are listed in Table 1.
Table 1. Equivalence classes in phantasmagoric fulleroids
|
G |
Vertices |
Edges |
Faces |
|
Le |
180; 3x{60} |
270; {30};2x{60};{120} |
92; {12},[5]; {60},[5]; {20},[9] |
|
Q |
200; {20}; 3x{60} |
300; 3x{60};{120} |
102; {12},[5]; {60},[5]; {30},[8] |
|
Ca |
260; {20}; 4x{60} |
390; {30};6x{60} |
132; {12},[5]; {60},[5]; {60},[7] |
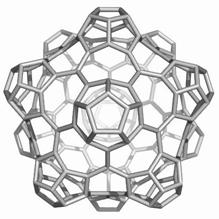
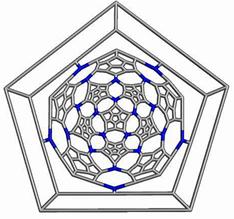
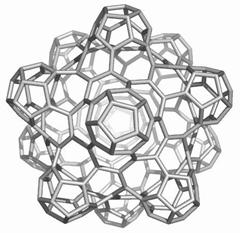
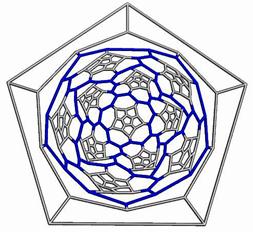
The two first operations Le and Q applied on the dodecahedron lead to achiral icosahedral cages, belonging to the Ih point group symmetry. However, the third transformation Ca preserves the icosahedral rotational symmetry but destroys all reflection operations thereby leading to the chiral point group I. More about the symmetry preserving by the above map operations the reader can find in ref [18].
According to the Clar theory, any polyhedral map may be looked for a perfect Clar PC structure [19], [20] which is a disjoint set of faces (built up on all vertices in M) whose boundaries form a 2-factor. Recall that a k-factor is a regular k-valent spanning subgraph. A PCS is associated with a Fries structure which is a Kekulé valence structure having the maximum possible number of benzenoid faces. Such structures represent total resonant sextet TRS benzenoid molecules and it is expected to be extremely stable, in the valence bond VB theory [21], [22]. Leapfrog Le is the only operation that provides PC transforms.
By extension, a corannulenic structure can be imagined 12 within the VB theory, either as (i) intersected, (ii) joint or (iii) disjoint units. While the case (i) is trivial, joint corannulenic JCor structures appear by Ca operation. A disjoint corannulenic DCor structure is a disjoint set of flowers, covering all the vertices in the molecular graph; it is a connected equivalent of the Fries structure. Only the (2,2) generalized [23] operation and/or (Le, Q) sequence provide a DCor covering [24]. Such a transform is necessarily associated with a PC structure, but the reciprocal is not always true. Observe the structure Dh(Le(D)), Figure 7, which is a disjoint structure of dodecahedron halves. In a next paper, Kekulé valence structure counting of Dh(E(Le(D))) will be discussed in detail into a future paper.
Our CageVersatile program enables performing the map operations on surfaces of any genus and vertex degree lattice.
Conclusions
Map operations enable construction of various cages starting from the Platonic solids. Moreover, they can be used as background for rationalizing the “in silico” building up of some previously published cages, like the phantasmagoric fulleroid of Fowler, Dh(E(Ca(D))). Topological symmetry data of the presented cages are available by performing some layer matrices on the associated graphs and their medial and dual transforms. The structure Dh(E(Le(D))), having disjoint dodecahedron halves, is a possible candidate to real molecular structure since the dodecahedron was already isolated as C20 molecule.
References
[1] Pisanski T., Randic M., Bridges between Geometry and Graph Theory, In: Geometry at Work: Papers in Applied Geometry, Ed. C. A. Gorini, Washington, DC: Math. Assoc. Amer., pp. 174-194, 2000.
[2] Euler L., Solutio problematis ad geometriam situs pertinentis (in Latin), Comment. Acad. Sci. U. Petrop., 8, 1736, p. 128-140.
[3] Euler L., Demonstratio nonnullarum insignium proprietatum quibas solida hedris planis inclusa sunt praedita, Novi Comm. Acad. Sci. Imp. Petropol., 4 (1752-1753), 1758, p. 140-160.
[4] Harary F., Graph Theory, Addison-Wesley, Reading, M.A., 1969
[5] Diudea M. V., John P. E., Graovac A., Primorac M., Pisanski T., Leapfrog and Related Operations on Toroidal Fullerenes, Croat. Chem. Acta, 76, 2003, p. 153-159.
[6] Fowler P. W., How unusual is C60? Magic numbers for carbon clusters, Chem. Phys. Lett., 131(6), 1986, p. 444-450.
[7] Fowler P. W., Steer J. I., The Leapfrog Principle: A Rule for Electron Counts of Carbon Clusters, J. Chem. Soc., Chem. Commun. 1987, p. 1403 - 1405.
[8] Fowler P. W., Rogers K. M., Eigenvalue relations for decorated trivalent polyhedra: connections between the fullerenes and their fulleren-yne and spheriphane relatives, J. Chem. Soc., Faraday Trans., 94, 1998, p. 1019-1027.
[9] Fowler P. W., Rogers K. M., Eigenvalue spectra of leapfrog polyhedra, J. Chem. Soc., Faraday Trans., 94, 1998, p. 2509-2514.
[10] Eberhard V., Zur Morphologie der Polyeder, Teubner, Leipzig, 1891.
[11] Goldberg M., A class of multi-symmetric polyhedra, Tohoku Math. J., 43, 1937, p. 104-108.
[12] Diudea M. V., Covering forms in nanostructures, Forma, 19, 2004, p. 131-163.
[13] Diudea M. V., Nanoporous carbon allotropes by septupling map operations, J. Chem. Inf. Model., 45, 2005, p. 1002-1009.
[14] Schlegel V., Theorie der homogen zusammengesetzten Raumgebilde, Verhandlungen der Kaiserlichen Leopoldinisch-Carolinischen Deutschen Akademie der Naturforscher, 44, 1893, p. 337-459.
[15] Diudea M. V., Molecular topology. 16. Layer matrices in molecular graphs, J. Chem. Inf. Comput. Sci. 34(5), 1994, p. 1064-1071.
[16] Diudea M. V., Topan M. I., Graovac A., Molecular topology. 17. Layer matrices of Walk degrees, J. Chem. Inf. Comput. Sci., 34(5), 1994, p. 1072-1078.
[17] Diudea M. V., Ursu O., Layer matrices and distance property descriptors, Indian J. Chem., Sect A, 42(6), 2003, p. 1283-1294.
[18] King R. B., Diudea M. V., The Chirality of Icosahedral Fullerenes: a Comparison of the Tripling (leapfrog), Quadrupling (chamfering), and Septupling (capra) Transformations, J. Math. Chem., 39(3-4), 2006, p. 597-604.
[19] Clar E., Polycyclic Hydrocarbons, Acad. Press, London, 1964.
[20] Clar E., The Aromatic Sextet, Wiley, New York, 1972
[21] Pisanski T., Fowler P. W., Leapfrog Transformation and polyhedra of Clar Type, J. Chem. Soc. Faraday Trans., 90, 1994, p. 2865-2871.
[22] Dias J. R., The most stable glass of benzenoid hydrocarbons and their topological characteristics - Total resonant sextet benzenoids revisited, J. Chem. Inf. Comput. Sci., 39(1), 1999, p. 144-150.
[23] Diudea M. V., Ştefu M., John P. E., Graovac A., Croat. Chem. Acta, 2006, 79(3), In press.
[24] Diudea M. V., Corannulene and corazulene tiling of nanostructures, PCCP, 7(20), 2005, p. 3626-3633.