Determination of Contact Angle from Contact Area of Liquid Droplet Spreading on Solid Substrate
Derrick O. NJOBUENWU1,2, Esio O. OBOHO1, Rhoda H. GUMUS2
1 Department of Chemical/Petrochemical Engineering, Rivers State University of Science & Technology, PMB 5080 Port Harcourt, Nigeria
2 Institute of Particle Science & Engineering, School of Process, Environmental & Materials Engineering, University of Leeds, Leeds LS2 9TJ United Kingdom
donadviser@yahoo.co.uk, Chedon@leeds.ac.uk, esioboho@yahoo.com, rhodagumus@yahoo.com
Abstract
Both complete and incomplete wetting were considered for the spreading of liquid drops on solid substrate. The liquid droplets were silicone oil, glycerine and hexadecane and the solid substrates are glass, polystyrene and polymethyl methacrylate (PMMA). Wetting was characterized by measuring the contact angle formed between the liquid drop and solid surface. Small droplets of constant volume were used for the measurements in order to minimize gravitational effects. The contact radius was obtained as a function of time by an image analysis system and used for the calculation of the contact area. The contact area was then used to determine the contact angle. The contact angles calculated from contact area are in good agreement with the experimental values.
Keywords
Contact Area, Contact angle, Spreading, Wetting, Surface tension, Liquid droplets
Introduction
Wetting of solid substrates by liquids is a fundamental phenomenon with relevance to both the technological and natural worlds [1]. Applications include the spreading behaviour of liquid coatings [2], as well as flows in oil reservoirs [3] and chemical reactors. Some biological application areas are motions in the tear film on the cornea of the eye, and flows on liquid covered membranes in the lungs. The spreading properties of agrochemicals such as pesticides and insecticides are important determinants of their effectiveness. Understanding and characterizing the wettability of solid surfaces is thus of significant importance. Wettability of solid-fluid-fluid interfacial phenomena is often characterized by measuring the contact angle formed between a liquid drop and a solid surface [4]. This measurement is considered to be a relatively simple, useful, and sensitive tool for assessing hydrophobicity or hydrophilicity of a surface, surface heterogeneity, surface roughness, solid surface energy, liquid surface tension, and line tension [5], although this is not straightforward but posses several questions to researchers.
One of the most popular methods for measuring the contact angle is the sessile drop method, which involves depositing a liquid drop on a smooth solid surface and measuring the angle between the solid surface and the tangent to the drop profile at the drop edge. If the drop stops spreading some time after deposition, the final angle can be easily measured through contact angle goniometry principles. This angle is called the advancing static contact angle qS. During the spreading, the angle measured is called the advancing dynamic contact angle q. It has been found experimentally that when the drop is spreading the contact angle is greater than qS and the drop keeps spreading until the angle decreases to qS.
First we studied the spreading of several liquids on different solid surfaces by considering the contact angle as an expression of wettability of the liquid on a solid surface, but there are many difficulties in finding the contact angles, these difficulties based on standards for measuring the contact angles for different liquids on different solid surfaces like defining the contact line of droplet surface to the solid surface. Therefore, the contact angle does not give the correct indication for the spreading of liquids. An alternating technique is introduced for measuring the spreading of liquids on solid surfaces, which is the contact area. Contact area is defined as the interface area between liquid and solid surfaces, this study apply contact area instead of the contact angle as a measure to indicate the wettability. It gives more accurate indication to the wettability and the rate of the spreading of different liquids on different solid surfaces.
Theory
Why do drops of different liquids deposited on identical solid substrate behave differently? Or, why identical droplets, for example, aqueous, deposited on different substrates behave differently? For example, a mercury drop does not spread on the glass substrate at all but forms a spherical drop with the contact angle bigger than 90o (Figure 1f). An aqueous drop deposited on the same glass substrate spreads out only partially down to some contact angle value, q, which is in between 0 and 90o (Figure 1c). However, an oil drop (silicone oil) deposited on the same glass substrate spreads out completely (Figure1b), contact angle decreases with time down to the zero value.
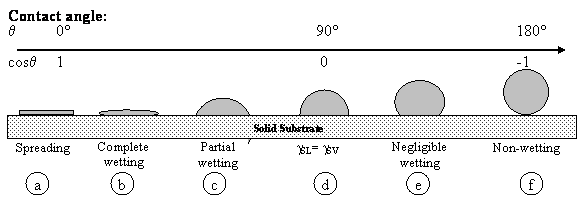
Figure 1. Liquid drop on solid
surface. The condition ![]() indicates that the solid is wet by the
liquid, and q > 90° indicates non-wetting, with the limits q = 0 and q=180°defining complete
wetting and complete non-wetting, respectively
indicates that the solid is wet by the
liquid, and q > 90° indicates non-wetting, with the limits q = 0 and q=180°defining complete
wetting and complete non-wetting, respectively
These three cases referred to supra are non-wetting, partial wetting and complete wetting, respectively. The same liquid can spread out completely or does not spread at all depending on the nature of the solid substrate. For example, water wets partially a glass and acrylic surfaces and does not wet Teflon surfaces [6]. It is obvious that complete wetting, partial wetting and non-wetting are determined by the nature of both the liquid and the solid substrate, and the contact angle. The equilibrium contact angle is given by well-known Youngs equation, γLV Cosqe = γSV γSL (Figure 2), where γSL, γSV, and γLV are solid-liquid, solid-vapour and liquid-vapour interfacial tensions which measure the free energy (per unit area), qe is the equilibrium contact angle [7].
The spreading parameter for non-equilibrium situation S = γSV - γSL - γLV is the energy gained when covering one unit area of the dry solid with a flat liquid film of macroscopic thickness. If S is negative, the situation where the solid is covered by a liquid film is not favourable. The equilibrium shape of the drop is a spherical cap (if small enough to ensure that gravity is negligible compared with capillarity), characterized by its equilibrium contact angle qe, and described by Youngs equation. For positive S, we have complete wetting, in which case a liquid drop will spread with time after its deposition on the surface, with its initially nonzero contact angle moving towards its limiting equilibrium, zero value.
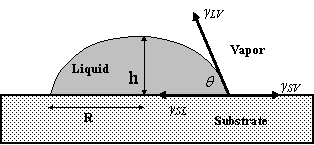
Figure 2. Interfacial tensions at the three phase contact line. R is the radius of the drop base and h is the height of droplet. The drop is small enough, thus, the gravity action can be neglected
For a small non-volatile liquid drop deposited onto a dry smooth and homogeneous solid surface, it deforms from its initial spherical shape, flattens to form a small cap of liquid and eventually reaches its equilibrium state. Figure 2 shows a schematic diagram of a liquid drop spreading on a solid surface. For simplicity, the drop is assumed to spread axisymmetrically on the horizontal surface. During the spreading process, the liquid drop will form the so-called dynamic contact angle with the solid surface, q(t), and spread out along the horizontal axis. With the increase of the contact radius of the drop, R(t), the drop will become thinner and its central height h(t), will decrease in order to meet the requirement of the constant liquid volume, V [8]. The spreading process will continue until the so-called equilibrium contact angle is achieved. This contact angle represents the wettability of the solidliquidfluid system and can be related to the interfacial tensions of the system by the well known Young equation γLV Cosq = γSV γSL where γSL, γSV, and γLV are solid-liquid, solid-vapour and liquid-vapour interfacial tensions, q is the contact angle [7].
Materials and Methods
The diagram of the experimental set-up is shown in Figure 3. All experiments were carried out at temperature 25 ± 0.5°C and 47% relative humidity. The liquids investigated on are Silicone oil, Hexadecane and Glycerine while the solid substrates include Glass, PMMA (poly methyl methacrylate) and Polystyrene. The fluids densities were measured by weight method and for measuring surface tension the Tensiometer (White, Elec.Inst, Co.LTD) was used. The viscosity was measured using the rheometer AR1000 (TA Instruments) at 25°C. The fluids properties measured are shown in Table 1.
Table 1. Selected fluid properties
|
Fluid |
Density (g/cm3) |
Surface tension (g/s2) |
Viscosity (g/cm s) |
|
Glycerine |
1.26 |
67.6 |
9.34 |
|
Silicone Oil |
0.96 |
22.5 |
99.0 |
|
Hexadecane |
0.774 |
32.1 |
3.1 |
The flat solid substrate, 1, was placed on a horizontal support with an optical screen, 2, underneath it during usage; a microlitre syringe of 5.0µl capacity, 3, was positioned at the centre of the substrate and connected to the micromanipulator, 4. The micromanipulator is used to adjust the position of the needle tip of the syringe carefully above the clean solid slide. The tip of the syringe was positioned a few micrometers away from the surface of the solid to eliminate impact effect when the droplet was released. The droplet volume was selected to be 1.5µl so that gravity effect is negligible. The spreading process was recorded using a CCD camera, 5 and a VHS recorder, 6. The camera has been equipped with filters, with a wavelength of 640 nm. Such an arrangement suppresses illumination of the CCD camera by the scattered light from the substrate and, hence, results in a higher precision of the measurements. The source of light used during experiments was from Oriel Lighting system, 7. The CCD camera and the VHS recorder were connected to a personal computer, 8. The VHS images were converted to avi film format using Pinnacle Studio 9 software. The avi files were converted to frames using Irfan View software. The images of spreading drop could be played back at 30 frames/sec. The radius of the drop, 9, with respect to time was measured using the image analysis software, ImageJ.
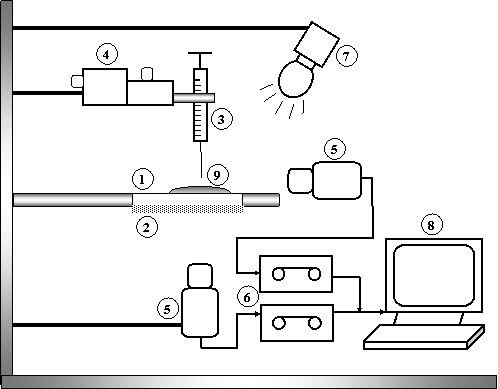
Figure 3. Experimental setup to measure contact angle from contact area: 1, Flat solid substrate; 2, Optical screen; 3, Microlitre screen; 4, Micromanipulator; 5, CCD video camera; 6, VHS recorder; 7, Light source; 8, Personal computer with frame grabber; 9 spreading drop
Results and Discussion
The spreading of liquid droplets over glass, polystyrene and PMMA substrates were investigated. Typical image frame acquired by the image analysis system described in the experimental procedure is displayed in Figure 4. The figure shows a printout of the plan view of a sample of experimental measurement for silicone oil spreading on glass substrate. Similar images (frames) were grabbed by the image analyser for glycerine and hexadecane drops on glass, polystyrene and PMMA substrate. The radius of spread was determined by the plan view and the contact angle for spreading of liquid droplets was determined from the side view. These data were digitalised and measured using the software as a function of time. The omissions of the other images were deliberate to avoid redundancy of images. Furthermore, a surface plot of a frame for Glycerine on Polystyrene is shown in Figure 5 to elucidate the understanding on surface geometry of liquid droplet undergoing partial wetting on solid substrate surface.

Figure 4. Silicon oil over glass surface
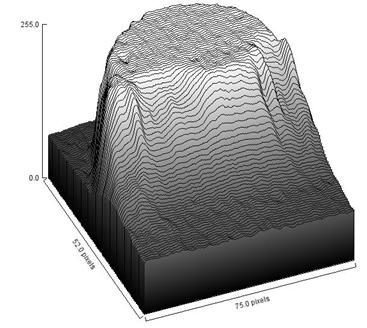
Figure 5. Surface Plot of Glycerine on Polystyrene
All liquids examined appeared to exhibit two stages of spreading and the base radius R follows scaling raw R ~ tn, where n < 1. Among all liquids tested, it was noted that only silicone oil exhibited complete spreading. Typical data representing each of these two cases are shown in Figure 6. Figure 6 shows silicone oil exhibited complete spreading and glycerine is noted to exhibit incomplete spreading. The spreading of the glycerine droplet took about one minute to reach equilibrium, the silicone oil continued to spread.
Theoretical contact angle was obtained from the contact
area by using the spherical cap approximation: ![]() . Table 2 shows results for
different liquids over different solids surface.
. Table 2 shows results for
different liquids over different solids surface.

Figure 6. Two stages of spreading showing complete and incomplete spreading
The spherical cap approximation provides a good correlation to obtain contact angle from contact area for relatively small contact angle. Irfan view software, a digital frame grabber was used to obtain images from side view of the CCD camera for measuring the contact angle. The ImageJ software was used to measure the contact angle as shown in Figure 7 for partial wetting of glycerine over glass. However, as contact angle increases which is an indication of increase in droplet height and decrease in the wetting area, the calculated contact angle deviates more from the experimental contact area. The error presented in Table 1 is calculated by taking the difference between the experimental measurements and the calculated angle. The error increases as the measured contact angle increases.
Table 2. Typical experimental and calculated data for various droplets on substrate
|
Liquid |
Substrates |
Final Area of Spreading, cm2 |
Contact Angle (Cal) |
Contact Angle (Exp) |
Error |
|
Glycerine |
Glass |
0.077 |
28.5 |
24.78 |
3.62 |
|
Glycerine |
PMMA |
0.042 |
70.64 |
63.76 |
6.97 |
|
Glycerine |
Polystyrene |
0.0324 |
104 |
83.88 |
20.12 |
|
Hexadecane |
Glass |
0.08656 |
23.93 |
23.30 |
0.63 |
|
Hexadecane |
PMMA |
0.14068 |
11.55 |
12.21 |
-0.66 |
|
Hexadecane |
Polystyrene |
0.20545 |
6.544 |
8.08 |
-1.536 |
This is attributed to the fact that Spherical cap approximation is based on the assumption h(t) << R(t), where h(t) and R(t) are the height of the spherical cap and the radius of the contact area, respectively. As contact angle increases, h(t) and R(t) values become closer thus, violating the spherical cap approximation assumption.

Figure 7. A sample showing determination of Contact Angle for glycerine over glass
It is also obvious that with the increase of the contact radius of the drop, R(t), the drop will become thinner and its central height h(t), will decrease in order to meet the requirement of a constant volume as shown in the droplet height profile in Figure 8 [8]. This is also significant in the contact angle meaning that the contact angle decreases with increase in the contact radius and decrease in the height of droplet. It is further suggested that for relatively small droplets, where gravitational effects are negligible, the macroscopic shape of the spreading droplet may be approximated by spherical cap geometry. This approximation relates the contact angle to the radius and the volume of the spreading droplet, i.e., the droplet height, h(t) = 1/2R(t)q, the contact area, A = 1/2πR(t)2 and its volume, V = 1/2 πh(t)R(t)2. Therefore the spreading law relates the volume of drops to the surface tension and viscosity of the drops and is given as R3m+1(t) = 1/μ(γtVm) [1], where theoretically for all cases of dry spreading m = 3.
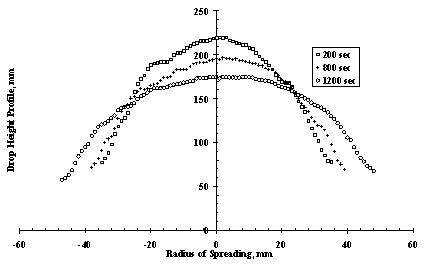
Figure 8. Time sequence height profiles of glycerine drop spreading on a flat PMMA substrate
Conclusion
Contact area gives good indication for the wettability and the low contact angle approximation is a good correlation to obtain contact angle from contact area for only small contact angle especially for h(t) << R(t).
Acknowledgement
The authors thank Rivers State Government of Nigeria for supporting this research in Loughborough University and Professor Victor M Starov of Loughborough University United Kingdom for his fruitful comments.
References
[1] de Gennes P. G., Wetting: Statics and Dynamics, Rev. Mod. Phys., 57(3), 1985, p. 827-863.
[2] Asthana R., Sobczak N., Wettability, Spreading, and Interfacial Phenomena in High-Temperature Coatings, JOM-e, 52(1), 2000.
[3] De Coninck J.; de Ruijter M., Voue M., Dynamics of Wetting, Current Opinion in Colloid and Interface Sci., 6, 2001, p. 49-53.
[4] Njobuenwu D. O., Nna E., The Effect of Critical Wetting Agent Concentration on Drilling Fluids Performance, J. Sci. & Tech. Research, 4(1), 2005, p. 65-71.
[5] Marmur A., Equilibrium and Spreading of Liquids on Solid Surfaces, Adv. Colloid and Interface Sci., 19, 1983, p. 75-102.
[6] Holdich R.; Starov V. M.; Prokopovich P., Njobuenwu D. O.; Rubio R.; Zhdanov S., Velarde M. G., Spreading of Liquid Drops from a Liquid Source, Colloids and Surfaces A: Physicochemical Engineering Aspects, 282283, 2006, p. 247-255.
[7] Adamson A. W., Gast A. P., Physical Chemistry of Surfaces; 6th Ed.; Wiley-Interscience, New York, 1997.
[8] Yongan Gu D. L., A Model for a Liquid Drop Spreading on a Solid Surface, Colloids and Surfaces A: Physicochemical and Eng Aspects 142, 1998, p. 243-256.
Nomenclature
qS = Advancing static contact angle; q = Contact angle; qe = Equilibrium contact angle; γLV = Liquid-vapour interfacial tension; γSL = Solid-liquid interfacial tension; γSV = Solid-vapour interfacial tension; A(t) = Area of spread; h(t) = Height of the spherical cap; R(t) = Radius of the contact area; S = Spreading parameter