Investigating the Effect of Changes in Furnace Operating Conditions Using the Well-Stirred Model
Shuaibu Ndache MOHAMMED
Department of Mechanical Engineering, Federal University of Technology, Minna, Nigeria
Abstract
An investigation into the effect of changes in furnace operating conditions employing the application of the ‘well-stirred furnace model’ is presented in this work. The operating conditions considered were the air preheats convection, fuel flow rates, excess air and air infiltration. For each of these conditions, the mean gas temperature, furnace output and thermal efficiencies were evaluated. The results show that apart from excess air and air infiltration, the effect of all the other operating conditions indicated an enhancement in the furnace performance.
Keywords
Well-Stirred Model, Furnace, Air Preheat, Convection, Air/Fuel Flow Rates, Excess Air, Air Infiltration.
Introduction
Furnaces have wide applications in engineering, with the main function of heating materials, often known as stock or charge, to a predetermined temperature and enthalpy.
Furnaces are used extensively especially in the steel making industry. The heat required for the process may be produced either by the combustion of a fuel or electrically by resistive, inductive, capacitative or arc heating (Gray and Muller, 1974).
Pantakar and Spalding (1972) developed a mathematical model for an open-flame furnace. This was a complex model as compared to the simple models which assume that the gas composition is uniform and that the temperatures of the gases and furnace surfaces remain invariant. The model was confined to laminar flows in three dimensional furnaces.
Pai, Michelfelder and Spalding in 1977 presented a report on the prediction of furnace heat transfer with a three dimensional mathematical model using finite difference solution procedure. The necessary differential equations were cast into a finite difference form with reference to a computational grid covering the flow field.
Simple mathematical models, giving average values of heat -flux in furnace, and hybrid models which predict heat-flux distributions using empirical methods, have been in existence for a long time. However, detailed calculations of the physical processes within the furnace have become feasible, with the aid of high speed digital computers and developments in numerical procedures. The physical processes occurring inside the furnace include: flow and mixing of the incoming streams and products of combustion; complex chemical reactions; and heat transfer by radiation, convection and conduction. In order to represent the furnace performance, it is therefore necessary to model each of these phenomena which occur simultaneously within the furnace (Kreith, 1976)
Tucker(1986) evaluated the direct exchange areas’ expressions by using a simple numerical integration technique. This result generated exchange areas for squares in mutually parallel and perpendicular, as well as for cubes and squares and for pairs of cubes in a rectangular frame work. The exchange areas are capable of being used in evaluating radiation exchange within rectangular gas-filled enclosures. These results are well suited for multi-zone radiation modeling.
The evaluation of the thermal performance of fuel-fired furnaces is dependent on an accurate calculation of radiant exchange between the combustion products, walls and stock within the heating chamber. This calculation is highly complex, however, with the increasing availability of high speed digital computers it is becoming feasible to employ numerical methods for the calculation of the heat-flux in furnaces. In order to employ the methods highlighted, it’s necessary that the shape factors be evaluated apriori.
Single Gas Model ( Well-Stirred Model)
In a batch furnace, the stock temperature changes with time. The simplest analysis of heat transfer in this type of furnace is the well-stirred model in which the combustion products filling the enclosure are treated as being isothermal and of constant composition and the wall and roof temperatures are considered constant. In a fuel-fired furnace with stock on the floor, the walls and roof may be treated as a single totally reflecting surface. Alternatively, if there is substantial heat loss through the walls or roof and if their emissivities and temperatures are different, they may be treated as separate isothermal surfaces. When the furnace length is comparable to the dimensions of its cross-section the furnace may be considered well-stirred. It can be used in cases where overall rather than local predictions are acceptable. This model permits evaluation of the effects of such factors as the input parameters or the fraction of wall-coverage by sink (stock) surfaces. Assumptions of well-stirred model are:
(1) Mixing is intense so that there are no concentration or temperature gradients in the furnace.
(2) Reactants-products can be considered as a single zone.
The problem is thus reduced to finding the gas temperature and hence the heat transfer
and furnace efficiency.
The heat release from gas can be obtained thus:
(1) Calculate the radiative heat transfer to the furnace surfaces from gases at gas temperature, Tg. This requires:
(a) Furnace geometry and surface properties;
(b) Gas composition (usually known for a specific fuel and combustion air);
(c) Flame luminosity (usually or often estimated from published data on flames).
(2) Calculate the convective heat transfer from gases at gas temperature, Tg. This requires the convective heat transfer coefficients which can be found from:
(a) Published data for flows over surfaces, tube banks, etc.;
(b) Published data for jets expanding in a duct;
(c) Mass transfer measurements on small scale models of furnace burner system.
Generally, the total heat transfer rate to all surfaces is given by:
|
QT = QR + QCONV |
(1) |
where QR and QCONV are the respective heat transferred by radiation and convection.
The heat transfer is balanced by heat lost from gases flowing through the furnace chamber, that is:
QL = heat input of incoming fuel + combustion air - heat content of waste gases
where QL is the heat lost from gases.
Usually, the heat balance can be solved graphically, see Figure 1(pp69); QS here refers to the heat transferred to the stock at gas temperature, Tg and Teg is the equilibrium furnace (gas) temperature.
Furnace efficiency is defined as the ratio of the heat transferred to stock to the total heat input of fuel. That is
|
ηth = QS/QIN |
(2) |
Lack of perfect mixing may be allowed for by allowing the mean gas temperature to be higher than the exhaust valve (TEX), for example,
|
Tg =TEX + 100 to 200°C |
(3) |
|
Tg = (TEX + TAF)/2 |
(4) |
|
T4g= 3(TAF – TEX)[1/(1/T3EX – 1/T3AF)] |
(5) |
where TAF is the adiabatic flame temperature.
The heat transferred is usually calculated at gas temperature Tg and the heat lost QL is given as:
|
QL = mCpTAF · TAF - mCpTEX · TEX |
(6) |
where CpTAF and CpTEX are the specific heats evaluated at TAF and TEX respectively.
The single gas zone model (relatively well-stirred) furnace model may be readily employed to investigate the effect of changes in the furnace operating conditions as follows:
Air Preheat
Changing the level of combustion of air preheat may well affect the rate of formation and extinction of soot in an oil-fired system. Thus, the flame emissivity will alter and strictly a new set of radiative calculations are required. However, in many cases we can assume this effect to be small so that the only significant changes in the calculation procedure are in the value of the adiabatic flame temperature, TAF, and the input heat content to the furnace.
Convection
In many conventional furnaces, radiation is the dominant heat transfer mechanism (90-95%). But in the well-stirred model, convection is very much taken into account. The effect of convection can thus be investigated.
Fuel Flow Rate
Modifying the fuel flow rate whilst maintaining the same air/fuel ratio changes the momentum of the jet so that the aerodynamic fuel/air mixing is unaltered. This affects the flame luminosity and hence the radiative heat transfer so that new heat transfer calculations are strictly necessary. For simplicity these are always ignored so that only the heat lost estimation is altered. Convection is assumed negligible, the adiabatic flame temperature, TAF, is unaltered so that the heat content of the exhaust at a particular gas temperature Tg is also unaltered.
Excess Air
Changing the air/fuel ratio (i.e. alteration of the amount of excess air) can modify jet momentum and mixing aerodynamics so that flame luminosity is to some extent changed. Consequently, once again, new radiation calculations are strictly necessary. If this is ignored the model must be amended to allow for the change in adiabatic flame temperature, TAF, and the heat input.
Air Infiltration
In this case any air leaking into the furnace does not contribute to the heat input so that TAF is reduced still further. Also, there is comparatively little effect on the radiative calculations. This is one of the furnace parameters with the greatest deleterious effect on efficiency, yet strangely it is often ignored.
Stock (or Sink) Temperature and Emissivity
Changes in these parameters obviously require new radiation calculations. Consequently, in view of the effort involved no quantitative estimates are made in this work. Nevertheless, from Hottel’s results, it is clear that the furnace efficiency increases as the stock temperature decreases. The efficiency also increases as the stock emissivity is increased so that materials with low surface absorptivities (emissivities) e.g. aluminium, are often heated in furnaces in which convection plays an important part.
Flame Emissivity
Changes in the furnace parameters often affect to some extent at least, the flame emissivity. This is also markedly affected by the type of fuel used. The British Non-Ferrous Metals Research Association have calculated the effect of changes in flame radiant properties, after initial rapid increase as the emissivity increases the efficiency is virtually insensitive to radiant properties. This justifies neglect of changes in radiative transfer in the earlier calculations.
Effect of Furnace Shape
For a given charge area, the thermal performance of a furnace to some extent depends on its shape, which alters the ratio of stock area to total internal area, the radiation beam length and the combustion gas flow pattern (not allowed for in single zone calculations). Too low a roof reduces the mean radiation beam length and also the refractory to stock area ratio, and thus reduces the heat flux to the stock. Nevertheless, a very high roof gives no thermal advantage (absorption of wall radiation by gases plus low temperatures in vicinity of roof due to gas flow) and a ratio of roof height to furnace width of 0.75 to 1.0 is probably sufficient.
The use of a single gas zone model to study changes in furnace shape should be treated with caution since the resultant changes in flow pattern can significantly affect the heat transfers.
Results and Discussion
The Well-Stirred Model Analysis
Results for this analysis are shown in Table 1. The effect of changes in furnace operating conditions shown in Table 1 is explained herein.
Effect of Air Preheat
The effect of combustion air preheat temperature is shown in Figure 1. It can be observed that any increase in air preheat temperature results in corresponding increase in both the furnace output and efficiency. In this analysis, new values of adiabatic flame temperature, TAF, and the input heat content to the furnace are always obtained for new air preheat temperatures.
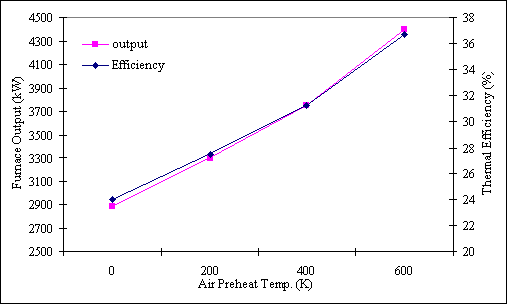
Figure 1. Effect of Air Preheat on Furnace Output and Thermal Efficiency Effect of Convection
The results of this effect are shown in Table 1. It can be seen that increasing the convective heat transfer coefficients, produces an increase in the efficiency and output. For each value of the convective heat transfer coefficient, new values of heat transmission to stock are obtained. Here the radiative calculation remains unaltered.
Effect of Fuel Flow Rate
Results of the effect of fuel flow rate on furnace performance are shown in Figure 2. It can be observed that an increase in fuel flow rate results in a decrease in efficiency. However, the furnace output increases simultaneously. It had been reported by experts in furnace design that unless other steps are taken to improve energy usage this decrease in efficiency is characteristics of furnaces.
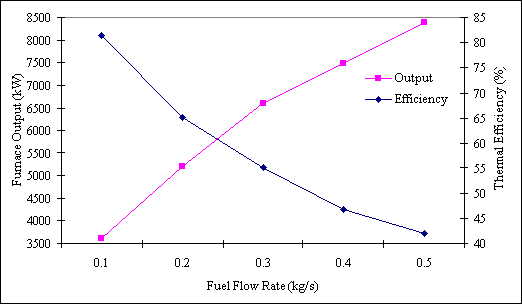
Figure 2. Effect of Fuel Flow Rate on Furnace Output and Thermal Efficiency
Effect of Excess Air
The effect of excess air on the thermal performance is presented in Figure 3. It was observed that increasing air intake, lowers the efficiency and output correspondingly. It was also observed that the higher the air preheats temperature, the higher are the corresponding efficiency and output values.
Effect of Air Infiltration
Effect of cold air leakage into the furnace chamber is illustrated in Table 1. This effect brings about decrease in efficiency and output of the furnace. Thus, it could be seen that cold air ingress has a greater effect than adding preheated excess air.
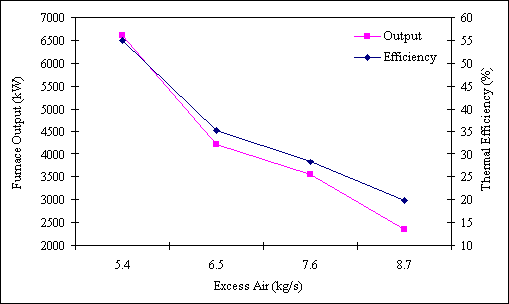
Figure 3. Effect of Excess Air Supply on Furnace Output and Thermal Efficiency
Table 1. Results of the Well – Stirred Model Analysis
|
Effect of |
Fuel Flow Rate (kg/s) |
Air Flow Rate (kg/s) |
Air Preheat Temp. (°C) |
Convective Heat Transfer Coeff. (kW/m2K) |
Mean Gas Temp. (K) |
Furnace Output (kW) |
Thermal Efficiency (%) |
|
1. Air Preheat |
0.3 |
5.4 |
0 200 400 600 |
0.10 |
1545 1641 1714 1785 |
2880 3300 3750 4400 |
24.00 27.50 31.25 36.67 |
|
2. Convection |
0.3 |
5.4 |
200 |
0 0.1 0.2 0.3 |
1609 1585 1520 1464 |
6460 6790 7290 7631 |
53.83 56.58 61.40 65.23 |
|
3. Fuel Flow Rate |
0.1 0.2 0.3 0.4 0.5 |
1.8 3.6 5.4 7.2 9.0 |
200 |
0 |
1463 1588 1648 1745 1790 |
3620 5205 6600 7485 8390 |
81.5 65.1 55.0 46.78 41.95 |
|
4. Excess Air |
0.3 |
5.4 6.5 7.6 8.7 |
200 |
0 |
1680 1488 1395 1180 |
6600 4230 3541 2360 |
55.00 35.25 28.30 19.75 |
|
5. Air Infiltration |
0.3 |
5.4 5.3 5.2 5.1 |
200 |
0 |
1750 1676 1625 1490 |
7900 6620 5630 3990 |
65.83 55.20 49.92 33.25 |
Conclusions
A ‘well-stirred furnace model’ for the investigation of the effects of furnace operating conditions, such as the air preheat, convection, air/fuel flow rates, excess air and air infiltration is undertaken.
The effect of air preheat on the furnace operating characteristics is found to be tremendously proportionate. It shows that as the air preheat temperature is increased, there occurs corresponding increase in the mean gas temperature, furnace output and thermal efficiency. The convective effect on the furnace performance results in lowering the mean gas temperature, while the furnace output and thermal efficiency are increased. The effect of the air/fuel flow rates also gave rise to an increase in mean gas temperature and furnace output but a reduction in the thermal efficiency of the system. Both the excess air and air infiltration reduce the mean gas temperature, furnace output and thermal efficiencies.
References
[1] Becker H. B., A Mathematical Solution for Gas-to-surface Radiative Exchange Area for a Rectangular Parallelopiped Enclosure Containing a Gray Medium, ASME, Journal of Heat Transfer, vol. 99, 1977.
[2] Gray W. A., Muller R., Engineering Calculations in Radiative Heat Transfer, Pergamon Press Ltd., Vol. 13, 1974, p. 1-75.
[3] Guruz H. K., Bac N., Mathematical Modeling of Rotary Cement Kilns by the Zone Method, The Canadian Journal of Chemical Engineering, Vol. 59, No. 4, 1976.
[4] Kreith F., Principles of Heat Transfer, IEP-A DUN-DONNELLEY, 3rd Edition, pp. 219-281, 1976.
[5] Patankar S. V., Spalding D. B., Mathematical Models of Fluid Flow and Transfer in Furnaces: A Review, Paper 2, 4th Symposium on Flames and Industry, 1972.
[6] Tucker R. J., Direct Exchange Areas for Calculating Radiation Transfer Rectangular Furnace, Journal of Heat Transfer, ASME, vol. 108, 1986, p. 707-710.