Mathematical Modelling and Simulation of Mobility of Heavy Metals in Soil Contaminated With Sewage Sludge
Muibat Diekola YAHYA, Jimoh ABDULFATAI
Department of Chemical Engineering,
Federal
mdoyejobi@yahoo.com, abdulfataijimoh@yahoo.com
Abstract
This paper is aimed at developing a model equation that can predict the
mobility of heavy metal in the soil contaminated with sewage sludge. The model equation
was developed and represented by the expression below ![]() . The developed equation was then simulated using MathCAD
2000 professional software. The experimental and model results obtained from
the simulation of the developed equation were compared numerically and
graphically. It was observed that there are reasonable levels of agreement
between the two results. The model revealed close fitting when compared with
the experimental results. This is further substantiated through the result of
the correlation coefficient analysis that was found to be unity for the
experiment. Thus, the model developed can be considered as a good
representation of the phenomenon of mobility of heavy metals in the soil.
. The developed equation was then simulated using MathCAD
2000 professional software. The experimental and model results obtained from
the simulation of the developed equation were compared numerically and
graphically. It was observed that there are reasonable levels of agreement
between the two results. The model revealed close fitting when compared with
the experimental results. This is further substantiated through the result of
the correlation coefficient analysis that was found to be unity for the
experiment. Thus, the model developed can be considered as a good
representation of the phenomenon of mobility of heavy metals in the soil.
Keywords
Heavy metals, Mobility, Sewage sludge, Simulation
Introduction
In process industries such as: fertilizer breweries, refineries, paper mills, textiles, chemical and petrochemicals, water could be used as coolant, process water, and raw material solvent etc. However, in the process of usage, industrial water becomes polluted and contaminated with various substances it comes in contact with and this gives rise to waste water, which consists of water with variety of potentially harmful substance which is the sources of environmental pollution. Sewage sludge is therefore, a by - product of purification of waste water. The resulting sewage sludge has significant organic mater content and contained macro and micro nutrient that are essential for plant growing. These heavy metals which may include cadmium, lead, arsenic etc are metallic element with relatively high atomic weight that can contaminate ground water, surface water, food etc. and have the potential to be toxic and relatively low concentration metal. All heavy metal exist in waste water in colloidal, particulate and dissolve phases, although in dissolve concentration the colloidal and particulate may be found in hydroxide, oxide, silicate or substance: or absorbed to clay, silica or organic matter.
Heavy metals released from sewage sludge are distributed throughout the soil system, while remaining in the soil solution as iron and organic and inorganic complexes some are mobile for uptake by plants (Hooda et al., 1997). This mobility and availability depends on several factor including soil texture and pH (Nouri., 1980 and Alloway., 1995). Mobile forms of metals release from sludge, which are not taken up by plant root, may move down the profile and reach the water table. This pollution of ground water may affect surface water and possibly portable water supplies. Changes can occur in chemical form and mobility of metal in the leachate, such as complexities of chalation which are usually the result of variation in PH or reduction-oxidation (Sims and Patrick., 1978). Several worker have already investigated the mobility of heavy metal in the soil amended with sewage sludge and concluded that only relatively small amount of metal were available for transport in the soil water immediately after sludge application (Slide and Kardos, 1977).
Giordano and Mortvedt (1976) show that under excessive leaching condition, movement of heavy metal in soil is somewhat greater from inorganic than from complexes sources found in sewage sludge. However, little or nothing had been done as regard to modeling of the process of mobility of heavy metals in the soil after the application of sewage sludge. This research work, therefore aimed at developing a mathematical model equation that shows the mobility of heavy metals in the soil amended with sewage sludge. This aim can be achieved through the realization of the following objectives:
· Collection of data showing the concentration of heavy metals at different percentage of sewage sludge amended to the soil with respect to distance and time.
· Development of mathematical model equations for the mobility of heavy metals in the soil amended with different percentage of sewage sludge.
· Simulation of the model equation using computer software programmed, MathCAD 2000 professional.
· Compare the simulated result with the experimental data.
Methodology
Preparation of sample
The soil and sludge were collected and prepared in
Modelling
Modelling of Mobility of Heavy Metals in Soil
Assumptions
The assumptions involved in this modelling of the mobility of heavy metals in the soil are thus:
1) Porous medium is homogeneous, isotropic, and saturated
2) There is no dispersion in the directions transverse to the flow direction
Modelling of the system
The equation that describes the flow of heavy metals material through soil is shown in equation 1 as (Vince DeCapio, 2003):
|
|
(1) |
where: C = Concentration of solute; DL = Hydrodynamic dispersion coefficient; vx = Pore velocity along flow path; ρb = solid density; θ = porosity for saturated conditions; C′′′ = Mass of solute sorbet per dry unit weight of soil.
This equation contains a term for dispersion, advection, and sorption (Vince DeCapio, 2003).
Knowing that
|
C" = kd · C |
(2) |
where kd = distribution coefficient
Equation (1) can then be written as:
|
|
(3) |
Since kd is a constant:
|
|
(4) |
Rearranging:
|
|
(5) |
and, rearranging further gives:
|
|
(6) |
that is:
|
|
(7) |
Let
|
|
(8) |
Equation can be written as:
|
|
(9) |
The equation is the same as:
|
|
(10) |
This is a second order differential equation which can be solved using any of the methods of solving second order differential equations. In order to solve the equation above, the left hand side is equated to zero as:
|
|
(11) |
assuming that:
|
|
(12) |
Equation (11) can be written as:
|
DL·m2 - vX·m = 0 m(DL·m - vX) = 0 m = 0 |
(13) |
or
|
(DL·m-vX) = 0 DL·m = vX |
(14) |
|
m=vX/DL |
(15) |
In other words,
|
m1 = 0 m2 = vx / DL |
(16) |
The complementary function which is given as:
|
C = A·e x m1 + B·e x m2 |
(17) |
can, therefore, be written as:
|
|
(18) |
|
|
(19) |
The particular integral is given as:
|
|
20 |
where R = Retardation factor
|
|
(21) |
|
|
(22) |
The general solution is the sum of the complementary function and the particular function as:
General solution = Complementary function + particular integer
|
|
(23) |
Boundary conditions:
|
At t = 0 x = 0 C = 0 |
|
That is:
|
0 = A + B·e0 + e0 0 = A + B · 1+ 1 0 = A + B + 1 A = -B - 1 |
(24) |
Also:
|
At t = ∞ X = ∞ C = 0
0 = A + B · 0 + 0 0 = A + 0 + 0 A = 0 |
(25) |
This means that from
A = -B - 1
0 = -B - 1
B = -1
Equation (23) can thus be written as:
|
|
(26) |
|
|
(27) |
|
|
(28) |
Finally, substituting the value of R yields:
|
|
(29) |
Equation (29) is, therefore, the model equation for the mobility of heavy metals in soils amended with sewage sludge.
Results and Discussion
The experimental results of this project are as shown graphically in figure 1-5. The experimental results show the presence of heavy metals in the soil as time increased from 0 to 8 months for different concentrations of sewage in the soil. For instance, the concentrations of cadmium, lead and nickel for ordinary soil (100% soil) at the initial time were found to be 0.007, 0.17 and 0.1 mg/m3 respectively. As time increased to 5 hours, the concentration of cadmium had increased to 0.008 mg/m3 while that of lead and nickel had decreased to 0.131 and 0.09 mg/m3 respectively ( McBride et al., 2004 ).
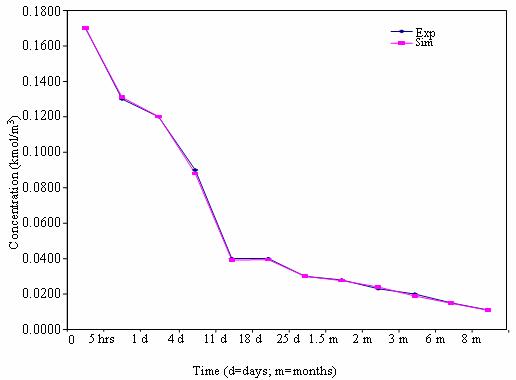
Figure 1. Mobility pattern of heavy metals in soil for 100% soil
In figure 2, the concentrations of heavy metals present in the soil when the sewage percentage was 10% in the soil were as shown.
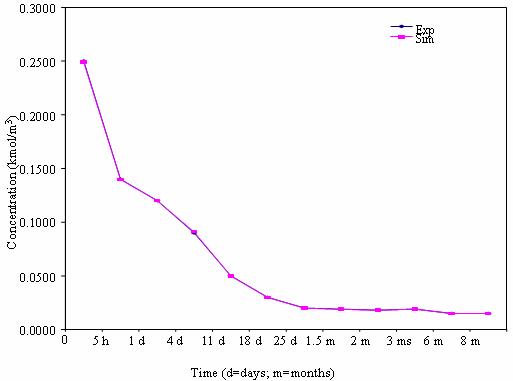
Figure 2. Mobility pattern of heavy metals in soil for 90% soil
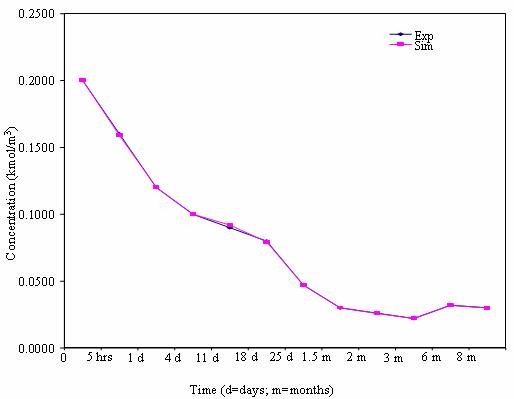
Figure 3. Mobility pattern of heavy metals in soil for 80% soil
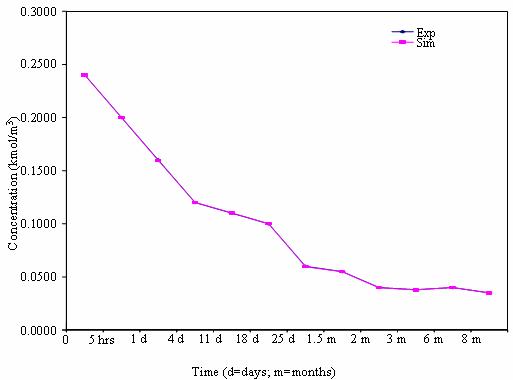
Figure 4. Mobility pattern of heavy metals in soil for 50% soil
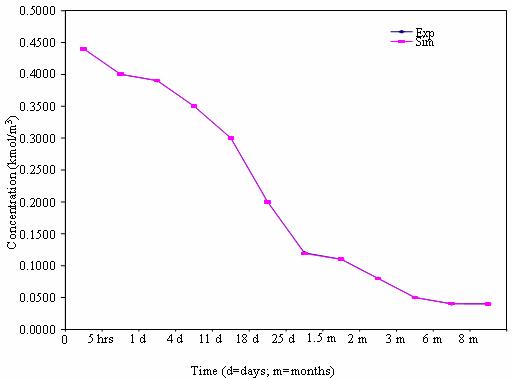
Figure 5. Mobility pattern of heavy metals in soil for 100% sewage
The results revealed (see figure 2) that the concentrations of heavy metals present in the soil at this percentage of 10% sewage in the soil were higher than that of the 0% sewage. For instance, the concentrations of cadmium, lead and nickel were found, at the 10% sewage in the soil, to be 0.12, 0.25 and 1.35 mg/m3 respectively. This shows that the more the percentage of sewage in any soil, the higher the concentration of heavy metals in that soil. (Richards et al., 2000). The trend of the concentration shows that the concentrations first increased and later decreased as the time increased. For instance, when the time was 5 hours, for soil with 20% sewage, the concentrations of cadmium, lead and nickel were found to be 0.10, 0.16, 2.1 mg/m3 respectively while the concentrations when the time increased to 1 day (24 hours) were found to decrease to 0.06, 0.12 and 1.25 mg/m3 respectively for cadmium, lead and nickel present in the soil.
Further, in some cases, for instance, in the table for 90% soil, when the time increased again, the concentration which decreased before then increased. The same trend was observed in the simulated results. The trend of the variation in concentration with respect to time and distance actually confirmed the mobility of heavy metals in the soil (Camobreco et al., 1996).
The comparisons between the experimental and simulated results are shown in the graph. The observations from the results showed there are good agreements between the experimental and simulated concentrations of heavy metals in the soil. For instance, for the 50% sewage soil, when the experimental concentration of cadmium was 0.12 mg/m3 at the end of 5 hours, the simulated concentration was 0.1199 mg/m3. At the same time of 5 hours when the experimental concentrations of lead and nickel were 0.2 and 6.6 mg/m3, the simulated concentrations were found to be 0.1999 and 6.6001 mg/m3 respectively.
The agreement between the experimental and simulated concentrations of heavy metals in the soil can also be confirmed by calculating the value of correlation coefficient on the two results (experimental and simulated). From the calculations, it was obtained that the correlation coefficient for the 0% sewage model was 0.9983 while that of the 10% sewage was 0.9999. Moreover, the correlation coefficients for 20% and 50% sewage sludge were calculated to be unity (1.0000). Finally, the value obtained for the correlation coefficient of the last one, which is 100% sludge, was also 1.0000.
Conclusion
The model equation developed for the mobility of heavy metals in the soil contaminated with sewage sludge is given as:
![]()
The analysis of the result shows that there is a very good level of agreement between the experimental and simulated results obtained. This can also be confirmed by the statistical analysis of the result through the correlation coefficient found to be 0.9983, 0.9999, and 1.000 for 100% soil, 90% soil and 50% soil respectively
In conclusion, the model developed can be considered to be a good representation of the phenomenon of mobility of metals in the soil.
References
1 Hooda P. S., McNulty D., Alloway B. J., Aitken M. N., Plant availability of heavy metals in soils previously amended with heavy application of sewage sludge, J. Sci of Food and Agric., 1997, 73, p. 446-454.
2 Alloway B. J., The mobilization of trace elements in soil, in prost, R.(ed.), contaminated soils, Les colloques, No.85, INRA, Paris, p. 133-145, 1998.
3 Sims J. L., Patrick Jr W. H., The distribution of micro nutrient cations in soil under conditions of varying redox potential and pH, Am. J. Soil Sci. Soc., 1978, 42, p. 258-262.
4 Sidle R. C., Kardos L. T., Aqueous release of heavy metals from two sewage sludges, Water Air Pollution, 1977, 8, p. 453 459.
5 Giordano P. M., Morvedt J. J., Nitrogen effects on mobility and plant uptake of heavy metals in sewage sludge applied to soil columns, J. Env. Qual., 1976, 5, p. 165-168.
6 McLaren R.G, Crawford P.V., Studies of copper1. The fractionation of copper in soils, J. Soil Sci., 1973, 24, p. 172-181.
7 Nouri J., Heavy metals in sewage sludge, soils amended with sludge and their uptake by crop plants, Ph.D. Thesis, University of London, 1980.
8 Vince DeCapio, Lead Sorption on Goethite Coated Silica Sand Columns, Environmental Engineering Science, Washington, USA, pp. 3-13, 2003.
9 McBride M. B., Richards B. K., Steenhuis T. S., Bioavailability and crop uptake of trace elements in soil column amended with sewage sludge products, Plant and Soil, 2004, 262, p. 71-84.
10 Richards B. K., Steenhuis T. S., Peverly J. H., McBride M. B., Effect of sludge processing mode, soil texture and soil pH on metal mobility in undisturbed soil column under accelerated loading, Environmental Pollution, 2000, 109(2), p. 327-346.
11 Camobreco V. J., Richards B. K., Steenhuis T. S., Peverly J. H., McBride M. B., Movement of heavy metal through undisturbed and homogenized soil columns, Soil Science, 1996, 161, p. 740-750.