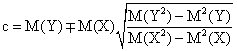The Jungle of Linear Regression Revisited
Lorentz JÄNTSCHI1, Sorana-Daniela BOLBOACĂ2
1Technical University of Cluj-Napoca, Romania
2Iuliu Haţieganu University of Medicine and Pharmacy, Cluj-Napoca, Romania
http://lori.academicdirect.org, http://sorana.academicdirect.ro
Abstract
Simple linear regression is reviewed. Some well known facts are analyzed from different approaches. Some new formulas and equations are posted and discussed.
Keywords
Simple Linear Regression, Least Squares Method, Independent and Dependent Variables
Hypothesis
Lets assume that we have two series of experimental measurements X = x1 xn and Y = y1..yn on which we suppose that a linear dependence exists:
|
X, Y linear dependent |
(1) |
Algebraic approach
The general formula for a linear dependence can be written as:
|
aX + bY + c = 0 Û aX + bY = -c |
(2) |
In terms of linear algebra our system (2) has three unknowns (a, b, and c) for only two known (X and Y). In order to provide a finite solution we must reduce the number of unknowns. Let us analyze the values of coefficients. Eight cases are presented in Table 1, for a, b, and c in terms of (0, ≠0):
Table 1. Cases for a, b, and c
|
Cases |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
a |
=0 |
≠0 |
=0 |
≠0 |
=0 |
≠0 |
=0 |
≠0 |
|
b |
=0 |
=0 |
≠0 |
≠0 |
=0 |
=0 |
≠0 |
≠0 |
|
c |
=0 |
=0 |
=0 |
=0 |
≠0 |
≠0 |
≠0 |
≠0 |
Case 1 is the trivial case (0 = 0, and it fit for any (X,Y) pair of data). Case 5 goes to an impossibility (c = 0 for c≠0). Cases 2 (aX = 0), 3 (bY = 0), 6 (aX + c =0), and 7 (bY + c = 0) are in disagreement with hypothesis (1).
For further discussions it remains only cases 4 (aX + bY = 0) and 8 (aX + bY + c = 0). Note that in these cases neither of coefficients is null. The following table contains variants of the above described two cases:
Table 2. Linear dependences for (X, Y)
|
aX+bY=0 (Case 4) |
aX+bY+c=0 (Case 8) |
|||||
|
0 |
1 |
2 |
0 |
1 |
2 |
3 |
|
aX+bY=0 |
X+nY=0 |
mX+Y=0 |
aX+bY+c=0 |
X+nY+p=0 |
mX+Y+p=0 |
mX+nY+1=0 |
In the table 3, elementary transformations to the equations from table 2 were applied. In addition, remarks are made.
Table 3. Cases analysis (variants of cases from table 2)
|
Variant |
Equation |
Remarks - statistical imposed assumptions |
|
4.0 |
aX+bY=0 |
particular case of 8.0 |
|
4.1 |
X=-nY |
X: dependent variable; Y: independent variable |
|
4.2 |
Y=-mX |
Y: dependent variable; X: independent variable |
|
8.0 |
aX+bY=-c |
both X and Y are dependent/independent variables |
|
8.1 |
X=-nY-p |
X: dependent variable; Y: independent variable |
|
8.2 |
Y=-mX-p |
Y: dependent variable; X: independent variable |
|
8.3 |
mX+nY=-1 |
particular case of 8.0 |
Note that we usually do (with any of well-known softwares) the variants 4.1 & 4.2 and 8.1 & 8.2. So, the most interesting to analyze are 4.0 and 8.3, which are particular cases of 8.0.
Usually, we assign as dependent variable a variable which comes from experiment and which is affected by experimental random errors, and we assign as independent variable a variable (which comes from experiment (?) - this statement open a discussion) and which is not affected by experimental random errors.
Nevertheless, what we must to do when both variables are affected by errors? Definitely, as we already seen in table 3, is not a good idea to use any of 4.1, 4.2, 8.1 or 8.2 assumptions.
Let us go back to our hypothesis (1) and let us set all our cases variants as f(vars,coefs) = 0 (table 4, as in table 2):
Table 4. Linear regression equation as function
|
Variant |
Equation |
Function for f = 0 |
|
4.0 |
aX+bY=0 |
f({X,Y},{a,b}) = aX+bY |
|
4.1 |
X+nY=0 |
f({X,Y},{b}) = X+bY |
|
4.2 |
mX+Y=0 |
f({X,Y},{a}) = aX+Y |
|
8.0 |
aX+bY+c=0 |
f({X,Y},{a,b,c}) = aX+bY+c |
|
8.1 |
X+nY+p=0 |
f({X,Y},{b,c}) = X+bY+c |
|
8.2 |
mX+Y+p=0 |
f({X,Y},{a,c}) = aX+Y+c |
|
8.3 |
mX+nY+1=0 |
f({X,Y},{a,b}) = aX+bY+1 |
As it can be observed from table 3, all other are particular cases of 8.0. So, we will discuss all in general related to 8.0.
A sum function can be constructed in terms of deviations from the model:
|
S = ∑|f({xi,yi},{a,b,c})|k, k > 0 |
(3) |
where sum are applied for all experimental measurements (from 1 to n). Note that in order to be consistent the definition (3), the modulus function must be used.
In terms of estimation, a, b, and c are called model parameters, and X, Y are dependent and/or independent variables (see also [1]). In terms of analysis, S is a function that depends on a, b and c as variables (unknown values) and X, Y and k as fixed (known) values. In terms of algebra, not all variables are allowed to vary in order to find a non-banal solution (null values - see also Eq. 4). Therefore, we must set one parameter.
Let us rewrite (3) in general case 8.0:
|
S(a,b,c) = ∑|aX+bY+c|k, k>0, one of a, b and c is set |
(4) |
How will affect a single measurement error the value of S? - see (5). Let us take a term of S:
|
Si(a,b,c) = |axi+byi+c|k |
(5) |
If xi = x0i+erxi, then Si = |ax0i+aerxi+byi+c|k = |aerxi+(ax0i+byi+c)|k. Thus, an absolute error of xi (erxi, not absolute in term of modulus, absolute in term of error, with same measurement unit with X) will be propagated as absolute error of S.
In some cases, we know more about our experimental errors.
Lets say, if we use an absolute method of measurement (such as mass measurement) then our error is an absolute one (in terms of measurement scale), and it remains the same as long as we use the same scale. In these cases, our preferred error expressions must be the absolute error. The opposite case, if we use a relative method of measurement (such as instrumental methods) then our error is a relative one (in terms of calibration accuracy), and it remains the same as long as we use the same calibration. In these cases, our preferred error expressions must be the relative error.
Nevertheless, we have two measured variables! What we have to do? - See (4, 6)
Coming back to the equation (4), we can weight the terms:
|
S(a,b,c) = ∑|aξX+bηY+c|k, k>0, ξ,η weights (known values) |
(6) |
where ξ = 1 if X has absolute errors and ξ = 1/M(X) if X has revalive errors and M(X) is the aritmetic mean of X values, and the same for η and Y.
What we have to do now? - To find the values of a, b, and c by imposing to S to be lowest:
|
S(a,b,c) = min |
(7) |
First pure mathematical problem comes now. Why? - Because we have modulus function f(∙) = |∙| in our formula, which is a continue and derivable function but with discontinue derivative. This is the reason for which we prefer even values for k (usually 2, we will see why). Anyway, (7) can be expressed in terms of derivatives:
|
∂S/∂coefs = 0 |
(8) |
The equation (8) is a system of equations, which for k≠2 is not linear. Taking as example the case 4.2 for k=4 and solving of (9) is equivalent to solving of:
|
m3(∑X4)+3m2(∑X3Y)+3m(∑X2Y2)+(∑XY3)=0 |
(9) |
For cases that are more general or for higher k values, solving of (8) leads to equations that are far more complicated. This is the reason for which we prefer k = 2. So, we fit now on well known minimizing of sum of partial least squares method. Rewriting of (6) for k = 2 leads to:
|
∑ξX(aξX+bηY+c) = ∑ηY(aξX+bηY+c) = ∑(aξX+bηY+c) = 0 |
(10) |
By using M(∙) as average operator M(∙) = ∑(∙)/n equations (10) became:
|
a∙ξ2∙M(X2)+b∙ξ∙η∙M(XY)+c∙ξ∙M(X) = 0 a∙ξ∙η∙M(XY)+b∙η2∙M(Y2)+c∙η∙M(Y) = 0 a∙ξ∙M(X)+b∙η∙M(Y)+c = 0 |
(11) |
The system (11) is not intended to be solved in its actual form, which it provides assuming the varying of all three parameters only the banal solution (0, 0, 0).
The case 4.1 (X+bY) are obtained from (11.2) when c=0 and a=1:
|
b = -(ξ/η)∙M(XY)/M(Y2) |
(12) |
The case 4.2 (aX+b) are obtained from (11.1) when c=0 and b=1:
|
a = -(η/ξ)∙M(XY)/M(X2) |
(13) |
Two remarks are immediate (from and for 12 and 13):
· weighting (ξ and η) does not affect the formulas for coefficients - identic est - the obtained formulas are transparent to weighting;
· is possible to construct another formula which it combine (12) and (13).
Rewriting of (12) and (13) without weighting and including the equation formulas goes to:
|
f({X,Y},{b}) = X-Y∙M(XY)/M(Y2), f({X,Y},{a}) = X∙M(XY)/M(X2)-Y, or X(Y) = - Y∙M(XY)/M(Y2) && Y(X) = - X∙M(XY)/M(X2) |
(14) |
Inversing the X(Y) and Y(X) functions:
|
X(Y)-1 = -X∙M(Y2)/M(XY) && Y(X)-1 = - Y∙M(X2)/M(XY) |
(15) |
From (14.1 & 15.2) and (14.2 & 15.1) it results that the coefficient can be obtained by applying of a mean function:
|
X(Y) = - Y∙Mean(M(XY)/M(Y2), M(X2)/M(XY)) |
(16) |
|
Y(X) = - X∙Mean(M(Y2)/M(XY), M(XY)/M(X2)) |
(17) |
But which mean is suitable? - The geometric mean provides same reversed result for:
|
X(Y) = - Y∙M0.5(X2)/M0.5(Y2) && Y(X) = - X∙M0.5(Y2)/M0.5(X2) |
(18) |
Formula (18) it represents a new formula for coefficients calculation. Which case can be assigned to (18)? - Only the remaining one, 4.0:
|
a= |
(19) |
The cases 8.1 & 8.2 are well known; it will not be discussed here.
The case 8.3 are obtained from (11.1) & (11.2) when c = 1:
|
a∙M(X2)+b∙M(XY)+M(X) = a∙M(XY)+b∙M(Y2)+M(Y) = 0 |
(20) |
Equation (20) leads to:
|
a = (M(Y2)M(X)-M(Y)M(XY))/(M(X2)M(Y2)-M2(XY)) b = (M(X2)M(Y)-M(X)M(XY))/(M(X2)M(Y2)-M2(XY)) |
(21) |
Also from (21) through extension, the following can be assigned to (8.0):
|
X∙(M(Y2)M(X)-M(Y)M(XY))+ + Y∙(M(X2)M(Y)-M(X)M(XY))+ + (M(X2)M(Y2)-M2(XY))=0 |
(22) |
Null intercept regression
Let us look more closely on case 4 with its sub-cases 4.0, 4.1 and 4.2.
· What we want? - We want a linear regression between X and Y.
· What we know? - We know at least that intercept coefficient is null.
· What we have? - We have at least a equation of type aX + bY = 0.
· What we cannot have? - We cannot have both parameters unknown.
Let us start from 4.0 (aX+bY=0) and apply the average operator. This leads to:
|
aM(X)+bM(Y)=0, for aX+bY=0 |
(23) |
What is wrong in our suppositions? - Remember, we already obtained some formulas for a and b (eq. 16-19). Answer: nothing is wrong! - Let us go back to table 3 and look more carefully to dependence/independence suppositions - here are the inconsistencies.
Now let us review our results for aX+bY=0:
· aM(X)+bM(Y) = 0 - main result, eq. (23)
o if X and Y are independent variables, then from eq. 23 solution is immediate:
|
a = |
(24) |
o if X is the dependent variable and Y is the independent variable, then (see also 17):
|
a = Mean(M(Y2)/M(XY), M(XY)/M(X2)), b = -1, for Y=Y(X) |
(25) |
o if Y is the dependent variable and X is the independent variable, then (see also 16):
|
b = Mean(M(XY)/M(Y2), M(X2)/M(XY)), a = -1, for X=X(Y) |
(26) |
o if X and Y are both dependent variables (see also 19):
|
a = |
(27) |
Few remarks can be made:
· The equations (25)-(27) assume that at least one of followings is (or a transformation applied to the data make it) true: M(X) = 0, M(Y) = 0, Mean(M(Y2)/M(XY), M(XY)/M(X2))M(X)-M(Y) = 0, Mean(M(Y2)/M(XY), M(XY)/M(X2))M(Y)-M(X) = 0.
· The mean function can be a weighted mean such as:
|
a = (1-f)∙M(Y2)/M(XY) + (f)∙M(XY)/M(X2), b = -1 |
(28) |
|
f portion (fraction) of X dependence in Y and (1-f) vice versa (1 ≥ f > 0.5) |
|
· or
|
b = (1-f)∙M(X2)/M(XY) + (f)∙M(XY)/M(Y2), a = -1 |
(29) |
f portion (fraction) of Y dependence in X and (1-f) vice versa (1 ≥ f > 0.5)
· Near to middle region (f ≈ 0.5) we can use any un-weighted mean. Followings are for Y=Y(X):
|
|
(30) |
and note the followings:
|
|
(31) |
|
|
(32) |
|
|
(33) |
More, a definition of PPM(∙,∙) similarly to AGM(∙,∙) leads to GM(∙,∙):
|
|
(34) |
Not null intercept formulas
The following table contains the obtained formulas (see algebraic approach section):
Table 5. Linear regression coefficients formulas
|
Variant |
Equation |
Function for f = 0 |
Coefficients |
|
8.0 |
aX+bY+c=0 |
f({X,Y},{a,b,c}) = aX+bY+c |
a = M(Y2)M(X)-M(Y)M(XY) b = M(X2)M(Y)-M(X)M(XY) c = M(X2)M(Y2)-M2(XY) |
|
8.1 |
X+nY+p=0 |
f({X,Y},{b,c}) = X+bY+c |
b = - (M(XY)-M(X)M(Y)) /(M(Y2)-M2(Y)) c = - (M(Y2)M(X)-M(Y)M(XY)) /(M(Y2)-M2(Y)) |
|
8.2 |
mX+Y+p=0 |
f({X,Y},{a,c}) = aX+Y+c |
a = - (M(XY)-M(X)M(Y)) /(M(X2)-M2(X)) c = - (M(X2)M(Y)-M(X)M(XY)) /(M(X2)-M2(X)) |
|
8.3 |
mX+nY+1=0 |
f({X,Y},{a,b}) = aX+bY+1 |
a = (M(Y2)M(X)-M(Y)M(XY)) /(M(X2)M(Y2)-M2(XY)) b = (M(X2)M(Y)-M(X)M(XY)) /(M(X2)M(Y2)-M2(XY)) |
Geometrical approach
In the following figure is depicted a (X,Y) plot, with a regression equation line (assigned with Y=aX+c), and a point Pi - of coordinates (xi,yi).
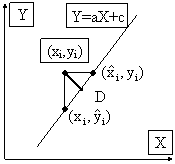
Figure 1. Geometrical interpretation of error estimates
Following are supplementary depicted:
· The intersection of X axis parallel with regression equation line - point of generic coordinates (xiest,yi) - from assumption that X=bY+c is the regression equation;
· The intersection of Y axis parallel with regression equation line - point of generic coordinates (xi,yiest) - from assumption that Y=aX+c is the regression equation;
· The intersection between perpendicularly from Pi to regression equation line.
The followings are true:
·
if S ← ∑![]() then a ←
then a ← ![]() , c ←
, c ← ![]()
·
if S ← ∑![]() then b ←
then b ← 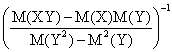 , c ←
, c ←![]()
Its easy to check that:
|
|
(35) |
which comes also from:
|
Y = aX + c
↔ |
(36) |
The
equations (35) and (36) prove that the chousing of S = ∑![]() for Y = aX
+ c is equivalent to chousing of S = ∑
for Y = aX
+ c is equivalent to chousing of S = ∑![]() for X = bY + c. So, the use
of square (xiest-xi)2 is equivalent
to case 8.2, and the use of square (yiest-yi)2
is equivalent to case 8.1.
for X = bY + c. So, the use
of square (xiest-xi)2 is equivalent
to case 8.2, and the use of square (yiest-yi)2
is equivalent to case 8.1.
If S ← PiD2 then:
|
S = ∑(axi-yi+c)/(a2+1) |
|
After calculation of ∂S/∂a and ∂S/∂c it results:
|
and c = M(Y) -
aM(X) for S ← |
(37) |
A formula that is even more complicated is obtained when offsets from S are choused to be with a slope of m. In this case, the formula for S is:
|
S ← |
(38) |
When m is independent to both a and c it results:
|
|
(39) |
Note that for the case of dependence between m and a, ∂S/∂m = 0 can be solved in two ways:
· if m is not a function of a then:
|
|
(40) |
· if m is a function of a then:
|
|
(41) |
By replacing of (27) in (24) it results:
|
S ← |
(42) |
Is the value of Pearson affected by how the slope and intercept are calculated?
The full question is: assuming that we have a measured X and Y and we want to estimate Y by using of regression equation which we obtained, how the calculated slope and intercept affects the Pearson r between measured Y and estimated Ŷ? - The answer is No, see below.
Let us take the squared Pearson coefficient between Y and Ŷ:
|
|
(43) |
By substituting of Ŷ = aX+c in (43) it results:
|
|
(44) |
Relation (30) prove that the values of a and c does not affect the correlation between measured Y and estimated Y, Ŷ.
About standard errors for regression parameters calculation
Standard error of the estimate (SEE) is used in association with t-test to see if a significant linear correlation exists. The SEE is related to r2 through:
|
|
(45) |
As we seen (Eq. 44), r2 does not depend on parameters values, so, also SEE does not depend on parameters values.
For two parameters type linear regression, standard errors for parameters are:
|
SE(a) = |
(46) |
For one type linear regression, standard errors for parameters are:
|
SE(a) = |
(47) |
Gauss-Markov theorem implications for linear regression
The Gauss-Markov theorem states that parameters that are obtained from minimizing the sum of the squared errors are Best Linear Unbiased Estimate (called BLUE). Of course, this conclusion comes in some assumptions. If the errors are independent and identically normally distributed, it is the maximum likelihood estimator. Loosely put, the maximum likelihood estimate is the value of parameters that maximizes the probability of the data that was observed.
The Gauss-Markov theorem shows that the least squares estimate is a good choice, but if the errors are correlated or have unequal variance, there will be better estimators. Even if the errors behave but are non- normal then non-linear or biased estimates may work better in some sense. So this theorem does not tell one to use least squares all the time, it just strongly suggests it unless there is some strong reason to do otherwise. Situations where estimators other than ordinary least squares should be considered are:
· When the errors are correlated or have unequal variance, generalized least squares should be used.
· When the error distribution is long-tailed, then robust estimates might be used. Robust estimates are typically not linear in y.
· When the predictors are highly correlated (collinear), then biased estimators such as ridge regression might be preferable.
We have described linear models. Parameters (a, b, and c) may be estimated using least squares. If we further assume that errors of estimation are normally distributed then we can test any linear hypothesis about parameters, construct confidence regions for parameters (from standard errors), make predictions with confidence intervals.
What can go wrong? - many things, unfortunately; we try to categorize them below:
· Source and quality of the data - how the data was collected directly effects what conclusions we can draw. We may have a biased sample, such as a sample of convenience, from the population of interest. This makes it very difficult to extrapolate from what we see in the sample to general statements about the population. Important predictors may not have been observed. This means that our predictions may be poor or we may misinterpret the relationship between the predictors and the response. Observational data make causal conclusions problematic - lack of orthogonality makes disentangling effects difficult; missing predictors add to this problem. The range and qualitative nature of the data may limit effective predictions. It is unsafe to extrapolate too much. Carcinogen trials may apply large doses to mice. What do the results say about small doses applied to humans? Much of the evidence for harm from substances such as asbestos and radon comes from people exposed to much larger amounts than that encountered in a normal life. Its clear that workers in older asbestos manufacturing plants and uranium miners suffered from their respective exposures to these substances, but what does that say about the danger to you or me?
· We hope that errors are normally distributed; but errors may be heterogeneous (unequal variance), may be correlated, and/or may not be normally distributed. The last defect is less serious than the first two because even if the errors are not normal, the parameters will tend to normality due to the power of the central limit theorem [A]. With larger datasets, normality of the data is not much of a problem.
· The structural part of y = aX+c model may be incorrect. The model we use may come from different sources:
o Physical theory may suggest a model; for example, Hookes law says that the extension of a spring is proportional to the weight attached. Models like these usually arise in the physical sciences and engineering.
o Experience with past data; similar data used in the past was modeled in a particular way. Its natural to see if the same model will work the current data. Models like these usually arise in the social sciences.
o No prior idea - the model comes from an exploration of the data itself.
Confidence in the conclusions from a model declines as we progress through these. Models that derive directly from physical theory are relatively uncommon so that usually the linear model can only be regarded as an approximation to a reality, which is very complex. Most statistical theory rests on the assumption that the model is correct. In practice, the best one can hope for is that the model is a fair representation of reality. A model can be no more than a good portrait [2].
Rescaling of X and Y and Ridge regression
When we want to rescale the X and Y values? - When we want to make comparisons between predictors; predictors of similar magnitude are easier to compare; a change of units might aid interpretability; numerical stability is enhanced when all the predictors are on a similar scale.
Rescaling X and Y leaves the t, F tests and r2 unchanged, and obtained new parameters are linear in rescaling. We already prove this for r2.
Ridge regression makes the assumption that the regression coefficients (after normalization) are not likely to be very large.
Let us go back to our model (2) rewritten in term of estimator and to be estimate. Then our estimator Ê and our to be estimated E are:
|
Ê(X,Y) = aX + bY + c, E(X,Y) = 0, Ê estimator of E |
(48) |
The sum function S from (3) became:
|
S = ∑(E(X,Y)-Ê(X,Y))2 = ∑(axi+byi+c)2 |
(49) |
The sum S can be averaged, when are called means-quared-error, MSE:
|
MSE = M((E(X,Y)-Ê(X,Y))2) |
(50) |
Let us assign another value to MSE:
|
MSE = (E(X,Y)-M(Ê(X,Y)))2 + M((Ê(X,Y)-M(Ê(X,Y)))2) |
(51) |
The formulas (50) and (51) are equivalent only if E(X,Y) is assumed to be constant (independent of X and Y).
In formula (51) two interesting terms appears [3]:
|
bias = (E(X,Y)-M(Ê(X,Y)))2, variance = M((Ê(X,Y)-M(Ê(X,Y)))2) |
(52) |
Note that occurs (53) and then model is unbiased.
|
if E(X,Y) = M(Ê(X,Y)) for all (X,Y) pairs Û bias = 0 |
(53) |
So, in the classifying of (53) our linear models can be splitted into biased (such as (28), (29), (30), (8.0), and (8.3)) and unbiased (such as (24), (8.1), (8.2), (37), and (38-39)).
Let us rewrite (52) using (49):
|
bias = (aM(X)+bM(Y)+c)2, variance = M((a(X-M(X))+b(Y-M(Y)))2) |
(54) |
So, the bias occurs when (M(X),M(Y)) Ï aX+bY+c = 0. However, an unbiased model may still have a large mean-squared-error if Ê(X,Y) it has a large variance. This will be the case if Ê(X,Y) is highly sensitive to the peculiarities (such as noise and the choice of sample points) of each particular training set and it is this sensitivity which causes regression problems to be ill-posed in the Tikhonov [4] sense. Often, however, the variance can be significantly reduced by deliberately introducing a small amount of bias so that the net effect is a reduction in mean-squared-error. This is the job of Ridge regression [5], a method for solving badly conditioned linear regression problems.
Bad conditioning means numerical difficulties in performing the matrix inverse necessary to obtain the variance matrix. It is also a symptom of an ill-posed regression problem in Tikhonov's sense and Hoerl & Kennard's method was in fact a crude form of regularization, known now as zero-order regularization [6].
Introducing bias is equivalent to restricting the range of functions for which a model can account. Typically, this is achieved by removing degrees of freedom. Examples would be lowering the order of a polynomial or reducing the number of weights in a neural network. Ridge regression does not explicitly remove degrees of freedom but instead reduces the effective number of parameters. The resulting loss of flexibility makes the model less sensitive. A convenient, if somewhat arbitrary, method of restricting the flexibility of linear models is to augment the sum-squared-error with a term, which penalizes large weights,
|
MSER = M((E(X,Y)-Ê(X,Y))2) + ρ2(a2(M(X2)-M2(X))+b2(M(Y2)-M2(Y))) |
(55) |
This is ridge regression (weight decay) and the regularization parameter ρ2 controls the balance between fitting the data and avoiding the penalty. A small value for means the data can be fit tightly without causing a large penalty; a large value for means a tight fit has to be sacrificed if it requires large weights. The bias introduced favors solutions involving small weights and the effect are to smooth the output function since large weights are usually required to produce a highly variable (rough) output function.
The use of ridge regression can be motivated in two ways. Suppose we take a Bayesian point of view and put a prior (multivariate normal) distribution on b that expresses the belief that smaller values of a and b are more likely than larger ones. Large values of ρ2 correspond to a belief that the b are really quite small whereas smaller values of ρ2 correspond to a more relaxed belief about a and b. Another way of looking at is to suppose we place to some upper bound on (a2+b2+c2) and then compute the least squares estimate to this restriction. Use of Lagrange multipliers leads to ridge regression. The choice of ρ2 corresponds to the choice of upper bound in this formulation. ρ2 may be chosen by automatic methods but it is probably safest to plot the values of parameters as a function of ρ2. You should pick the smallest value of ρ2 that produces stable estimates of parameters.
Discussion
The use of PM(∙,∙,∙), eq. (30) - Hölders mean - it opens an interesting discussion. We already had seen that:
· if S ← (Y-(aX+c))2 then:
o if c = 0 then:
§
a = ![]() (or a =
(or a = ![]() from M(Y) = aM(X))
from M(Y) = aM(X))
o else:
§
a = ![]() , c =
, c = ![]()
· if S ← (X-(Y-c)/a)2 then:
o if c = 0 then:
§
a = ![]() (or a =
(or a = ![]() from M(Y) = aM(X))
from M(Y) = aM(X))
o else:
§
a = ![]() , c =
, c = ![]()
If we put back our formulas to the geometrical interpretation, following result is obtained (Figure 2):

Figure 2. Penality function S vs. vertical and horizontal offsets
In addition, we had seen that (eq. 33):
·
![]()
·
![]()
So, if we put our formulas for, let us see, slope obtained from this two different aproaches in previous formulas, it result that:
|
|
(56) |
|
|
In fact, through equation (56) we construct a function (PM) which sweeps the entire right angle (figure 3).
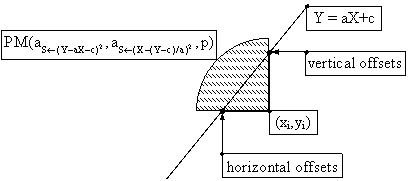
Figure 3. Hölder mean, acting for linear regression
As consequence, all obtained formulas for slope (and for intercept, when is not set null) can be obtained from a Hölder mean:
|
|
(57) |
where the obtained formula (57) was completed with negative slope cases. Of course, when slope is negative, then are choused the negative solution of (57).
Finally,
note that equation (57) has a solution in ![]() and this is unique if and
only if |aS| are in between:
and this is unique if and
only if |aS| are in between:
|
|
(60) |
and as we
already seen (eq. 33), for ![]() admits also p → 0 as limit
solution.
admits also p → 0 as limit
solution.
An interesting formula results also as consequence of (8.1), (8.2), (30), (33) and construction from Figure 2: calculation of slope using GM and intercept using M(Y)=aM(X)+c, where sign of a and c respectively, are given from quadrant of scatter plot:
|
|
(61) |
References
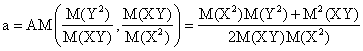
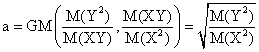
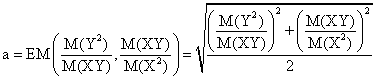
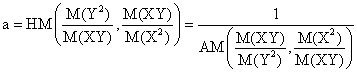
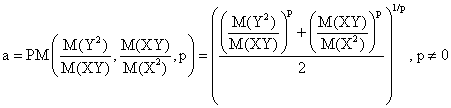
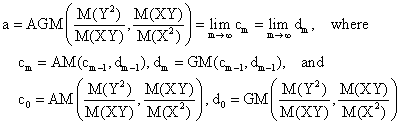
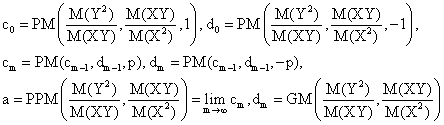
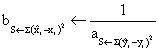 and
and 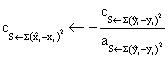 when X
↔ Y
when X
↔ Y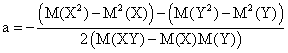
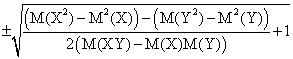
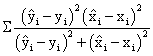
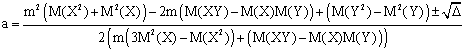
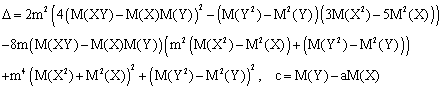
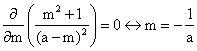 (perpendicular
offsets)
(perpendicular
offsets)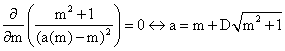 , C any
constant
, C any
constant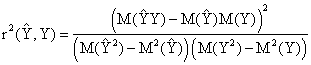
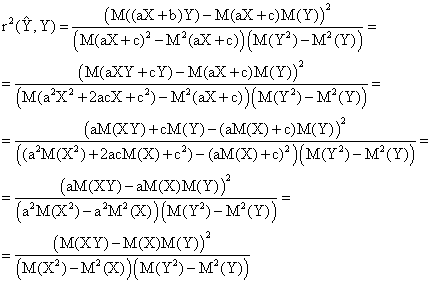
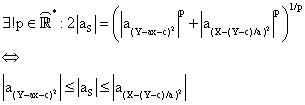
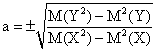 ,
,