Reliability Evaluation for Optimizing Electricity Supply in a Developing Country
Mark Ndubuka NWOHU
Department of Electrical/Computer Engineering, Federal University of Technology,
Minna, Niger State
Abstract
The reliability standards for electricity supply in a developing country, like Nigeria, have to be determined on past engineering principles and practice. Because of the high demand of electrical power due to rapid development, industrialization and rural electrification; the economic, social and political climate in which the electric power supply industry now operates should be critically viewed to ensure that the production of electrical power should be augmented and remain uninterrupted. This paper presents an economic framework that can be used to optimize electric power system reliability. Finally the cost models are investigated to take into account the economic analysis of system reliability, which can be periodically updated to improve overall reliability of electric power system.
Keywords
System Reliability; Cost Models; Economic Analysis; Reliability Evaluation, System Security.
Introduction
The electric utility is expected to provide continuous and quality of electric service to their customers at a reasonable rate by making economical use of available system and apparatus. To maintain reliable service to customers, the utility has to have adequate redundancy in its system to prevent a component outage becoming a service interruption to the customers, causing loss of goods, services or benefits.
Reliability costs are used for rate reviews and request for rate increases. Therefore in order to calculate the cost of reliability, the cost of an outage must be determined. In his papers, Nwohu, M.N. [1] discussed a simple technique which can be adopted to determine the cost of outages in relation to loss of goodwill, loss of production and damaged goods. The economic analysis of system reliability can also be a very useful planning tool in determining the capital expenditures required to improve service reliability by providing the real value of additional investments into the system. Lastly, expectation indices, which are most often used to express the adequacy of the generation configuration, characterize future system performance in a satisfactory manner.
Definition of Reliability
The term reliability has a very wide range of meanings and cannot be associated with a single specific definition such as that often used in the mission-oriented sense. It is therefore necessary to recognize its extreme generality and to use it to indicate, in a general rather than specific sense, the overall ability of the system to perform its function. But from the engineering point of view, reliability can simply be defined as the probability that an item or a collection of items will perform satisfactorily, under specific conditions during a given period [2].
This system reliability can further be discussed under two basic aspects of power systems, viz, system adequacy and system security. Security relates to the ability of the system to respond to disturbances arising within that system. It is therefore associated with the response of the system to whatever disturbances it is subject and loss of major generation and transmission facilities. Adequacy, on the other hand, has to do with existence of sufficient facilities within the system to satisfy the consumer load demand. It is therefore associated with static conditions that exclude system disturbances. In the domain of adequacy assessment, the probabilistic techniques are usually available for power system reliability evaluation.
Reliability Evaluation
Reliability with regard to electric power systems involves collection of outage data, which includes frequency of interruptions and their total duration and evaluating the system designs. The system designs evaluated are compared with alternative circuit configurations, sectionalizing provisions, protective schemes and automation.
The system can be evaluated by using the conditional probability method [2] which determines a proper component of a given power system, say Ci, being short-circuited first (i.e. substituted by a component that never fails) and then open-circuited (i.e. assumed to be a failure). Therefore the probability of system success (i.e. the system reliability) can be expressed thus as.
|
Rsys=P(System operatesçCi operates)P(Ci)+P(System
operatesçCi fails)P( |
(1) |
The probability of system failure (i.e. the system unreliability) can be expressed as
|
P ( |
(2) |
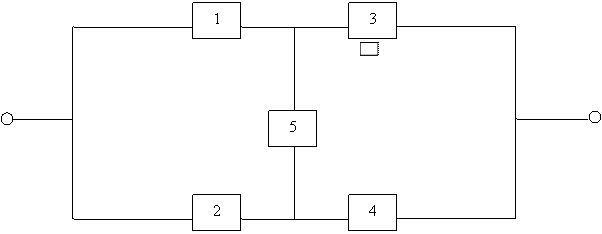
Figure 1. A hypothetical bridge type system network
Considering a hypothetical bridge-type system network shown in figure 1, at least one of the paths comprising the following components Ci C3 , C2 C4 , C1 C5 C4 and C2 C3 is good for system success and therefore the system operates. So the best choice for component Ci is component 5 (i.e. C5) which could be short circuited or open - circuited. Therefore the system reliability can be expressed as
Rsys = P (system
operates çC5 operates) P (C5)
+ P (system operates çC5 fails)
P (![]() )
)
= Rsys (if C5 operates) R5 + Rsys (if C5 fails) Q5
where:
· R5 = reliability of component 5
· Q5 = Unreliability of component 5
· Rsys (if C5 operates) = (1-Q1Q2) (1-Q3 Q4)
· Rsys (if C5 fails) = (1- R1 R3) (1-R2 R4)
Therefore,
|
Rsys = [(1- Q1 Q2) (1- Q3 Q4)] R5 + [(1- R1 R3)] Q5 |
(3) |
Similarly, the system unreliability can be calculated from equation (2), thus
|
Qsys = [(1-R2 R2) (1-R3 R4)] R5 + [(1- (1- Q1Q3) (1- Q2 Q4)] Q5 |
(4) |
Network Cost Modeling
In power systems planning, it is often convenient to standardize network voltages and ratings. These standard network configurations enhance the modeling of costs of networks using regression analysis [3]. The cost of substations and cables or conductors in distribution networks is mostly considered and which can be closely idealized by straight lines (see figure 2). The cost of a substation basically consists of two variables, viz, fixed cost (i.e. the cost of land, civil works, building, etc.) and variable cost (i.e. cost which depends on the rating and voltage). The variable cost represents the cost of extra amounts of copper or aluminium required for increased rating and additional amount of insulation required for higher voltages. Therefore the mathematical expression of the total substation cost is derived thus:
Css = Cfs + Cvs R
where:
· Css = Total substation Cost
· Cfs = Fixed Cost
· Crs = Cost which depends on voltage (i.e. variable cost)
· R = Rating.
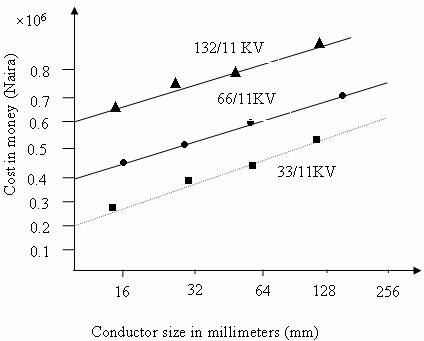
Figure 2. Typical Cost modeling of network
Conclusions
The cost modeling of network is highlighted in this paper to give an insight of what is likely to be the standard network configurations. It is discovered that the operation of optimal networks depends largely on the extent of optimization study carried out, starting from the primary distribution system consisting of trunk primary circuits, laterals and distribution transformers with the main substation situated at a suitable place.
In a developing country, it is observed that erratic supply of electricity seriously undermine the reliability of electric power supply for industrial and domestic uses. However, this paper discusses the probability method used in evaluating the economic analysis of system reliability to optimize electric power supply to electricity users.
References
1. Nwohu M. N., Evaluation of Costs of Outages on National Electric Power Authority (NEPA) and Industrial Consumers in Nigeria, a paper presented on a seminar, Faculty of Engineering, Nigerian Defence Academy, August 1995.
2. Gouen T., Electric Power Transmission System Engineering, John Wiley & Sons Publishing Co. Ltd., pp. 438-439, 1998.
3. Pable A. S, Electric Power Distribution Systems Tata magraw Hill publishing Co. Ltd, p. 109, 1984.
4. Boess M. R. et all, Optimized Distribution and Sub transmission Planning by digital Computer, IEEE Trans. PAS, October, 1986, p. 1083.