Impact of Wind Power on the Angular Stability of a Power System
Djemai NAIMI1, Tarek BOUKTIR2
1 Department of Electrical Engineering, University of Biskra, Algeria
2 Department of Electrical Engineering, University of Oum El Bouaghi, Algeria
naimi_djemai@yahoo.fr, tarek.bouktir@esrgroups.org
Abstract
Wind energy conversion systems are very different in nature from conventional generators. Therefore dynamic studies must be addressed in order to integrate wind power into the power system. Angular stability assessment of wind power generator is one of main issues in power system security and operation. The angular stability for the wind power generator is determined by its corresponding Critical Clearing Time (CCT). In this paper, the effect of wind power on the transient fault behavior is investigated by replacing the power generated by two main types of wind turbine, increasing gradually a rate of wind power penetration and changing the location of wind resources. The simulation analysis was established on a 14 bus IEEE test system by PSAT/Matlab, which gives access to an extensive library of grid components, and relevant wind turbine model.
Keyword
Angular Stability, CCT, Wind Turbine, Wind Penetration, PSAT.
Introduction
A power network is a complex system, which is vulnerable to disturbances. A transient short circuit fault is a very common disturbance in a power system [1]. It upsets the rotating machines in the vicinity of the fault, causing the speeds of these machines, and the power flows in the network to oscillate. When the short circuit is cleared by disconnecting the faulted line, the generators that have accelerated will decelerate and come back into synchronism with the rest of the system. If they do not, and the system becomes unstable, there is a risk of widespread blackouts and of mechanical damage to generators. So the critical clearing time (CCT) is the maximum time interval by which the fault must be cleared in order to preserve the system stability [2, 3].
There is no doubt that wind power will play a predominant role in adding clean and nonpolluting energy to the country’s grid. However, as more wind turbines are connected to the grid, their impact on the power quality of services populated with wind generation is becoming more evident, so it is important to analyze the transient stability of power system including wind power stations [4].
A three-phase fault is applied to a 14 bus IEEE test system, and cleared by disconnecting the affected line.
In this paper, the focus is limited to determine Critical Clearing Time (CCT) for the several cases by observing the transit behavior simulation of a test system during grid faults using a Matlab power system analyze toolbox (PSAT) [5].
The structure of this paper is as follows. First, the wind model is described briefly; also the wind turbine concepts are described. Then, the test system and the applied models are presented. The oscillation of a group of generators during a fault is analyzed by observing the transient behavior for following cases:
A- Changing a wind source locates.
B- Different generator technologies.
C- Increasing gradually a rate of wind sources penetration.
To conclude, the results are clarified on the basis of existing theories and comparison between different cases in order to choose a best case and avoid a worse one.
Wind Model
Wind energy is transformed into mechanical energy by means of a wind turbine whose rotation is transmitted to the generator by means of a mechanical drive train.
The wind-power equation [6, 7] is given by:
![]()
where ρ is the air density, r is the turbine radius, ν is the wind speed, and Cp is the turbine power coefficient which represents the power conversion efficiency and it is a function of the ratio of the rotor tip-speed to the wind speed, termed as the tip-speed-ratio (TSR).
Such disturbances are the most common in the grid, the grid disturbances considered in this paper are of short duration, maximum a few hundreds of milliseconds. Since the considered grid disturbances are much faster than wind speed variations, the wind speed can he assumed constant. Therefore, natural wind variations need not be taken into account. The wind speed is set to a constant 15 m/s.
Turbine Models
There are many different types of wind turbines in use around the world, each having its own list of benefits and drawbacks [8]. In this paper two main types of wind turbines are taken into account:
· A constant speed wind turbine (Fig. 1a), which consists of a grid coupled short-circuited induction generator [9]. The wind turbine rotor is connected to the generator through a gearbox. The power extracted from the wind is limited in high wind speeds using the stall effect. No active control systems are used.
· A variable speed wind turbine with wound rotor induction generator (Fig. 1b) – doubly-fed induction generator (DFIG). The rotor winding is supplied using a back-to-back voltage source converter [10]. As in the first case, the wind turbine rotor is coupled to the generator through a gearbox. In high wind speeds the power extracted from the wind is limited by pitching the rotor blades.
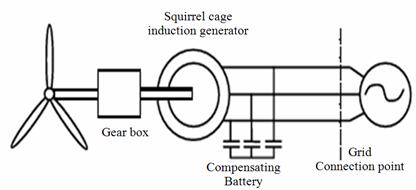
Figure 1a. Squirrel cage induction generator
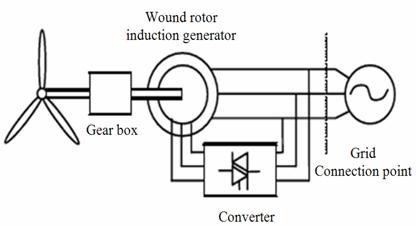
Figure 1b. Doubly-fed induction generator
Test System
The test system for this study is presented in Fig. 2, it is derived from IEEE test system; this network consists of 14 buses, 5 generators, 11 loads and 83 branches. The transformers connecting generators to the grid are adjusted accordingly. Wind turbines are the 2 MW machines described above in section 2.
Note that the generators do not represent a single machine but a group of strongly coupled generators and for this test system the total power is divided as follow:
Table 1. Active power of test system generators
|
Generator N° |
1 |
2 |
3 |
4 |
5 |
|
Power(MW) |
615 |
60 |
60 |
25 |
25 |
The disturbance investigated is a three-phase short-circuit on Bus number 2. This three-phase fault represents the most severe disturbance for transient stability problems.
It must be noted that all simulations are developed by PSAT (version 2.0.0 β1).
Results and Discussions
Impact of Location
In order to assume the impact of the wind power to angular stability of power system, we included a three phase symmetrical fault then we calculate the CCT corresponding to a case without wind source and others cases where a wind source is connected to test system by different Buses.
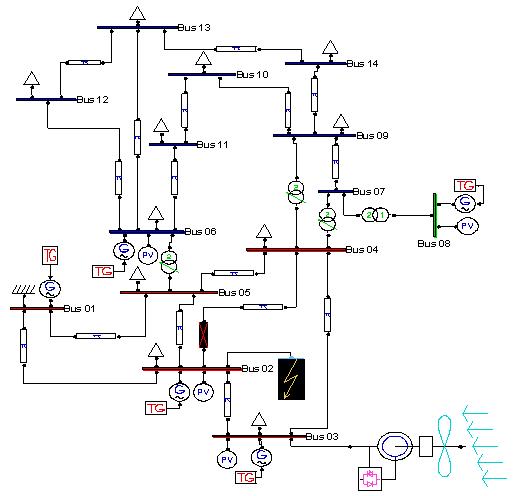
Figure 2. Base case
Without a Wind Source
The Base Case represents the normal operation of the system without any wind power connected to the system. The critical fault clearing time (CCT) can be determined using transient simulations [3]. For this case, the result is CCT = 196 ms. Fig. 3 shows the speed generators in comparison for a fault clearing time close to the critical clearing time.
In Fig. 3b, the fault introduced has duration of t = 197 ms, so the time is exceeding the stability limit of CCT.
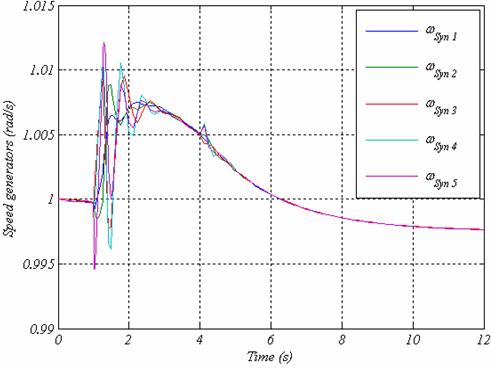
Figure 3a. Rotor speed of all generators at t = 196 ms
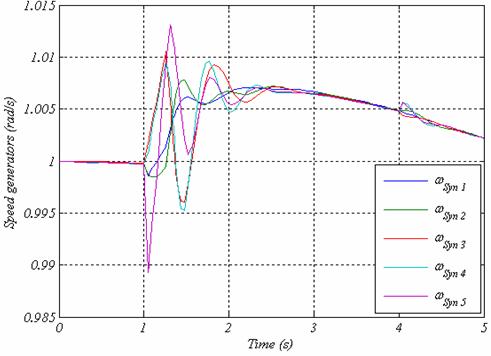
Figure 3b. Rotor speed of all generators at t=197 ms
With a Wind Source
After that, one wind turbine generator is connected to system through a transmission line on different buses for evaluating their effect to the angular stability.
Table 2. Results from the simulations for the angular stability on different locations
|
Bus number |
Bus 1 |
Bus 3 |
Bus 8 |
Bus 14 |
|
CCT (ms) |
186 |
187 |
263 |
220 |
Compared to the previous case where any wind source was connected, the integration of wind source has increased the transit stability when it was connected at BUS 8 or BUS 14, but on the contrary for cases of BUS 1 and BUS 3, so there is no general statement possible, if wind generation improves transient stability margins or if the impact is rather negative. The answer depends on location of wind resources and the problem has to be analyzed individually for each case.
Effect of Type of Generator Technology
In order to determine the effect of type of generator technology to transit behavior of grid, two types of generators are studied with keeping the same fault and the same location of wind source.
Case 1: Fixed Speed
The critical fault clearing time (CCT) can be determined using transient simulations. For this case, where wind source is connected to Bus N°3 the result is CCT = 187 ms. Fig. 4 shows the speed rotor of all generators in comparison for a fault clearing time close to the critical clearing time.
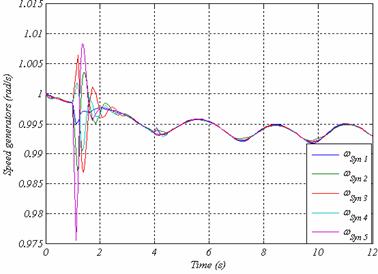
Figure 4a. Rotor speed of all generators at t=187 ms
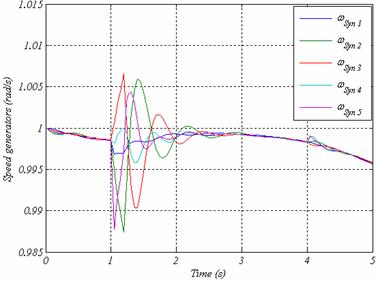
Figure 4b. Rotor speed of all generators at t=188 ms
Case 2: Variable Speed (DFIG Technology)
The fixed speed generator added to Bus 3 is now disconnected and substituted by a doubly-fed induction generator (DFIG) having a same power (2MW). Thus, the change in the technology can be considered and analyzed. The analysis of the CCT results in an increased stability limit compared to Case 1 with only fixed speed generators in service. The time increases to CCT = 216 ms as shown in figure 5 .This means, that the transient network stability is enhanced when DFIG are connected instead of fixed speed generator.
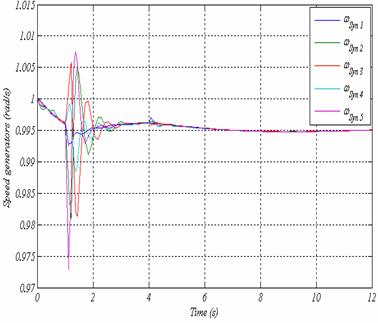
Figure 5a. Rotor speed of all generators at t=216 ms
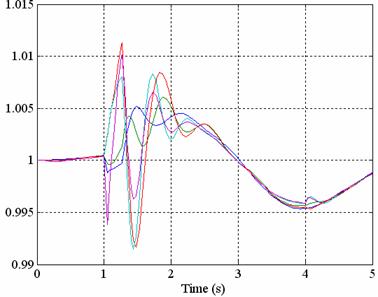
Figure 5b. Rotor speed of all generators at t=217 ms
Comparison
To analyze this effect more in detail, table 3 shows the CCT values for DFIG generator ( variable speed) and induction generator(fixed variable) on different locations.
Table 3. CCT for two types of turbine technology on several buses
|
Bus N° |
1 |
3 |
8 |
14 |
|
CCT for fixed speed(ms) |
186 |
187 |
263 |
220 |
|
CCT for variable speed(ms) |
286 |
216 |
300 |
227 |
According to results, it is very clearly that the DFIG generator increase the critical clearing time, consequently this type of generator presents best performance than a squirrel cage induction generator concerning the angular stability of grid connected to wind power, it is evident that the Wind power generation with DFIG provides better performance for angular stability after fault clearance owing to its ability to control reactive power.
Effect of wind penetration
In this section, the effect of wind power on the oscillations is investigated by gradually increasing the rate of wind source penetration while observing the transit behavior of system [11].
Table 4. CCT for different rates of wind power penetration
|
Rate of wind sources penetration (%) |
3.18 |
6.7 |
14.01 |
21.65 |
≥ 22 |
|
Installed capacity of Wind sources (MW) |
24.96 |
52.59 |
109.90 |
169.95 |
≥172 |
|
CCT (ms) |
271 |
229 |
151 |
97 |
00 |
From the results, it is concluded that the effect of wind power on power system oscillations depends on the rate of wind power penetration, it has been proven that a high level of wind power penetration such in our case study is must be lower than 22 % of total grid power, otherwise the test system lost its stability.
Conclusion
This paper has mainly focused on the assessment of the angular stability by determinate a critical clearing time (CCT), This was done by observing the behavior of speed generators of the test system included a three phase fault when changing several parameters.
According to previously simulations, the following conclusions are obtained:
· There is no general statement possible, if wind generation improves transient stability margins or if the impact is rather negative. The answer depends on location of wind resources and the problem has to be analyzed individually for each case.
· The effect of type of generator technology in transit stability is very significant and the DFIG generator presents more performance than a squirrel cage induction generator.
· It has been proven that a high level of wind power penetration destabilize the power system when a very large part of the synchronous generation capacity is replaced by wind power.
Finally, it very important to note that a calculation of a critical clearing time (CCT) in all previous simulations was done by several times which represent a wasting of effort and time so a numerical method of computation of (CCT) is very required for such transit stability studies.
References
1. Sun T., Chen Z., Blaabjerg F., Voltage recovery of grid-connected wind turbines after a short-circuit fault, Annual Conference of the IEEE Industrial Electronics Society, Virginia, USA, 2003.
2. Saffet Ayasun, Yiqiao Liang, Chika O. Nwankpa, A sensitivity approach for computation of the probability density function of critical clearing time and probability of stability in power system transient stability analysis, Applied Mathematics and Computation, 2006, p. 563.
3. Salman S. K., Teo A. L. I., Investigation into the Estimation of the Critical Clearing Time of a Grid Connected Wind Power Based Embedded Generator, Proceedings of the IEEE/PES transmission and distribution Conference and exhibition 2002, Asia Pacific Pucific, Vol. 11, 2002, p. 975-980.
4. Jauch C., Sørensen P., Norheim I., Rasmussen C. Simulation of the Impact of Wind Power on the Transient Fault Behavior of the Nordic Power System, Electric Power Systems Research, VOL: article in press, available online 24 March, 2006, p. 135-144.
5. Federico Milano, Power System Analysis Toolbox Documentation for PSAT version 2.0.0 β1, July 9, 2006.
6. Soerensen P., Hansen A.D., Pedro Andre Carvalho Rosas, Wind Models for Prediction of Power Fluctuations of Wind Farms, J. Wind Eng. Ind. Aerodyn, 2002, 90, p. 1381-1402.
7. Tang Hong, WuJunling, Zhou Shuangxi, Modeling and Simulation for Small Signal Stability Analysis of Power System Containing Wind Farm, J. Power System Technology, 2004, 28(1), 38-41.
8. Hansen A.D., Sørensen P., Iov F., Blaabjerg F., Initialisation of Grid-Connected Wind Turbine Models in Power-System Simulations, Wind Engineering, 2003, 27(1), p. 21-38.
9. Nandigam K., Chowdhury B. H., Power flow and stability models for induction generators used in wind turbines, IEEE Power Engineering Society General Meeting, 2004, 2, p. 2012-2016.
10. Hansen A. D., Michalke G., Fault ride-through capability of DFIG wind turbines, Renewable Energy, 2007, 32, p. 1594-1610.
11. Ha L. T., Saha T. K., Investigation of Power Loss and Voltage Stability Limits for Large Wind Farm Connections to a Sub-transmission Network, Power Engineering Society General Meeting, 2004, 2, p. 2251-2256.