A New Constructive Method for Electric Power System Reconfiguration Using Ant Colony

Habib HAMDAOUI, Samir HADJERI and Abdelkader ZEBLAH^*

Electrotechnic Laboratory, Djilali Liabès University,Sidi Bel Abbes, Algeria

E-mail: azeblah@yahoo.fr (^*corresponding author)

          Abstract

This electric power distribution system delivers power to the customers from a set of distribution substations. While the transmission lines are configured in a meshed network, the distribution feeders are configured radially in almost all cases. The proposed problem in this work is to determine the optimal topology among a various alternatives. This problem is known as a problem of total investment-cost minimization, subject to power constraints. In fact, the paper addresses an ant colony met-heuristic optimization method to solve this combinatorial problem. Due to the variation of demand, the reconfiguration may be considered in two different situations: in the system planning or system design stage. The proposed met-heuristic determines the minimal investment-cost system configuration during the considered study period to satisfy power transit constraints. The algorithm of ant colony approach (ACA) is required to identify the optimal combination of adding or cut off feeders with different parameters for the new topology design.

Keywords

Ant Colony Algorithm; Alternative; Optimization; Topology; Design.

Introduction

            The electric power distribution system usually operates in a radial configuration, with tie switches between circuits to provide alternate feeds. The costs of losses would be minimized if all switches were closed and there are no loops, but this is not done because it complicates the system’s protection against overcurrents. Whenever a component fails, some of the switches must be operated to restore power to as many customers as possible. As loads vary with time, switch operations may reduce costs of losses in the system. Both of these are applications for reconfiguration.

            Reconfiguration is the process of operating on remote elements (switchs) to change the circuit topology. In this case, the problem is combinatorial, which precludes algorithms that guarantee a global optimum. Most existing reconfiguration algorithms was devoted and classified into two categories. In the first, branch exchange, the system operates in a feasible radial configuration and the algorithm opens and closes candidate switches in pairs. In the second, loop cutting, the system is completely meshed and the algorithm opens candidate switches to reach a feasible radial configuration.

            This paper uses an ant colony algorithm to solve this problem. The idea of employing a colony of cooperating agents to solve combinatorial optimization problems was recently proposed in [1]. The ant colony approach has been successfully applied to the classical traveling salesman problem TSP [2] and [3], to the quadratic assignment problem [4] and [5], and to scheduling [6, 7]. Ant colony shows very good results in each applied area. It has been recently adapted for the network design. The ant colony has algorithm also been adapted with success to other combinatorial optimization problems such as the vehicle routing problem [8], telecommunication networks management [9], graph coloring [10], constraint satisfaction [11] and Hamiltonian graphs [12]. The ant colony algorithm has not yet been used for the new reconfiguration design.

Summuray of previous work

            Last decade much works was devoted to network reconfiguration and optimization. Less effort has been expended to use an heuristic or meta-heuristic algorithms to replace the combinatorial one. Among theses algorithm:

1- Simulated annealing is not a reconfiguration algorithm by itself, but is a modification to some other basic algorithm [13]. Its purpose is to avoid being trapped in local minima, by not always taking the best choice at each step. Under simulated annealing, a random choice is accepted with a probability that decreases exponentially with each iteration. Simulated annealing has more potential to find the global optimum, though this cannot be proven. It is readily applied on decision tree or branch exchange methods, by adding an extra outer loop to the basic algorithm.

2- Genetic algorithms have become very popular as a method of finding global optimums. As applied to reconfiguration [14], the switch states are encoded in strings of 0/1 "chromosomes",and a population of, for example, 50 topologies is built at random. At each iteration, two parent topologies are selected at random for crossbreeding, which is a process of combining the chromosomes according to some defined algorithm. Then mutation, a random alteration of some chromosomes, may occur with a certain probability. If the resulting child is better, it replaces an existing topology in the population of 50. This process of crossbreeding continues for a number of iterations. The population also has to be re-seeded periodically with random strings to avoid

3- Neural networks have been applied to recognize a load pattern from feeder measurements and other data, then select a pre-analyzed topology and switching strategy to reconfigure the network for loss reduction [15]. It’s necessary to discretize load levels and combine similar topologies, otherwise the training sets become too large. The neural network serves as a state estimator but doesn’t analyze the topologies, so this method is not really applicable to the problem statement.

4- Discrete ascent optimal programming (DAOP) has been applied to optimal load flow and phase balancing for distribution systems.

Approach

            As the problem formulated in this paper is a complicated combinatorial optimization one, an exhaustive examination of all possible solutions is not realistic considering reasonable time limitations. Because of this, the ACA will be adapted to the reconfiguration problem to find optimal or nearly optimal solutions to be obtained in a short time. It was proven that the newer developed meta-heuristic method has the advantage to solve the problem without the limitation. Ant colony algorithm is inspired by the behaviour of real ant colonies that exhibit the highly structured behavior. Ants lay down in some quantity an aromatic substance, known as pheromone, in their way to food. An ant chooses a specific path in correlation with the intensity of the pheromone. The pheromone trail evaporates over time if no more pheromone in laid down by others ants, therefore the best path has more intensive pheromone and higher probability to be chosen. During the optimization process, artificial ants will be used to evaluate the shortest paths of a given electrical structure system. To do this, a fast procedure of optimization is developed.

Problem Formulation

The reconfiguration problem is very important in power industry. It is a well known combinatorial optimization problem where the design goal is achieved by discrete remote on opening and closed switches lines. In this paper, the problem is to find the minimal cost configuration of electrical network system under power transit constraints. The electrical network structure is sketched in figure 1. The system consist of mashed lines of n lines and switches (sw) (i = 1, 2, …, n) in loop arrangement.

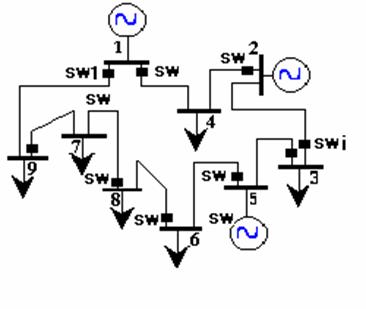
Figure 1. Electrical Topology

Find the merit system configuration that provides the minimal total cost under power transit constraint. This problem can be started as below:

Minimize

(1)

Subject to

(2)

:Investment component function of line length ($/Km).

: Investment component function of line section ($/Km. mm²).

I_ij: Currant transit from node i to node j (Ampere).

n: Total nodes of electrical network.

m_i: Number of nodes connected to node i.

L_ij: The length of the bows (i, j) (Km).

            In addition, we define separately the power losses cost and the line investment cost by:

(3)

And

(4)

C₁: Represents power losses cost.

C₂: Represents line investment cost.

Then the determination of the merit configuration of the meshed network is also expressed by determining the flow of currents I_ij in a manner such as the conventional cost of the network is:

(5)

Load Characteristics

            Loads vary with time of day, day of the week, and season. Each type of load (residential, commercial, industrial) has a different time profile, and each feeder serves a different mix of loads. Therefore, the load pattern on each feeder varies constantly, and with a different variation on each feeder. This creates an opportunity to constantly keep losses at a minimum by reconfiguring the feeders during the day. Automatic switches and control systems must be installed to perform this distribution automation, at a cost that must be balanced against the savings in losses. The distribution system should be operated at minimum cost, subject to a number of constraints:

1. Power Transit, 2. all loads are served, 3. over-current protective devices are coordinated, 4. lines, transformers, and other equipment within current capacity limits, 5. voltage drop within limits.

Ant Colony Optimization Approach

            The problem formulated in this paper is a complicated combinatorial optimization problem. The total number of different solutions to be examined is very large, even for rather small problems. An exhaustive examination of the enormous number of possible solutions is not feasible given reasonable time limitations. Thus, because of the search space size of the problem, a meta-heuristic can be developed. This meta-heuristic uses the ant colony optimization method. The work by [16] presents examples of applications of this meta-heuristic to various combinatorial optimization problems. The ant colony can be seen as a simulation of a set of agents that cooperate to find a solution of an optimization problem by means of uncomplicated communications. The inspiration was taken from observation of the behavior of real ants. Ants are social insects living in colonies. Ants can cooperate effectively to make some tasks. For instance, almost blind ants can find the shortest route paths from their colony to feeding sources and back. It was observed that a moving ant deposits some pheromone (in variable quantities) on the ground, hence marking the path it follows. Next ants moving towards the feeding area can identify the pheromone left by the previous ant, decide with high probability to follow it, and reinforce the select trail with its own pheromone. This form of indirect communication mediated by pheromone lying is called stigmergy. Ants make use of pheromone in order to find a shortest path between two points connected with two branches. Since there is no pheromone, ants decide randomly which path to choose. Therefore, more pheromone deposited on the lower path new ants chooses this path more willingly.           This important feature of real ants’ behaviour is called autocatalytic mechanism. To coupling between autocatalityc mechanism and the implicit evaluation of solution can be used in ant algorithm. It means that the more ants follow a trail, the more attractive that trail becomes for being followed. The probability with which an ant decides on a path increase with the number of ants that earlier used the same path.

The Ant Colony Algorithm

Step1. Initialize:

Set t:=0 {t is the time counter},

For every path (i,j) set an initial value tij (t) and set Dtij (t,t+n):= 0,

Place b_i(t) ants on every bus i {b i (t) is the number of ants on bus i at time t},

Set s:=1 {s is the tabu list index}

For i:=1 to n do

For k:=1 to b_i (t) do

tabu_k (s):= i {starting bus is the first element of the tabu list of the k-th ant}.

Step2. Repeat until tabu list is full {this step will be repeated (n-1) times}

2.0. Set s:=s+1

2.1. For i:=1 to n do {for every bus}

For k:=1 to b_i (t) do {for every k-th ant on bus i still not moved}

Choose the bus j to move to, with probability p_ij (t)

Move the k-th ant to j {this instruction creates the new values b_j (t+1)}

Insert bus j in tabu_k (s).

Step3. For k:=1 to m do {for every ant}

Compute L^k {it results from the tabu list}

For s:=1 to n-1 do {scan the tabu list of the k-th ant}

Set (h,l):=(tabu_k (s),tabu_k (s+1))

{[h, l] is the edge connecting bus s and s+1 in the tabu list of ant k}

L^K: represent the length crossed by the K-th ant.

Q: represent the amount of pheromone laid by the K-th ant.

Step4. For every edge (i,j) compute tij (t+n) according to equation (1)

Set t:=t+n

For every path (i,j) set Dtij (t,t+n):=0.

Step5. Memorize the shortest path found up to now

If (NC < NC_MAX ) or (not all the ants choose the same tour) {NC is the number of algorithm cycles;

in NC cycles are tested NC·m tours}

then

Empty all tabu lists

Set s:=1

For i:=1 to n do

For k:=1 to b i (t) do

tabu_k (s):=i {after a tour the k-th ant is again in the initial position}

Goto step 2

else

Print shortest tour and Stop.

Illustrative Example

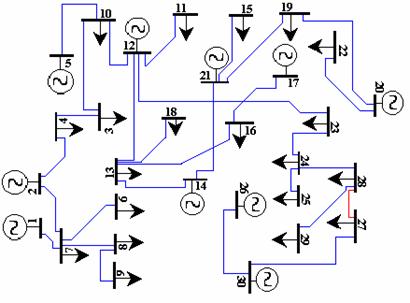
            The implantation is chosen on real network Algerian national network, made by ten (10) generating stations and twenty (20) consumer nods as sketched in fig. 2, the distribution system with ten sources and several switching devices. Swi. At the initial state, all the switches are closed and the system is operating in loop configuration.

Figure 2. Meshed Electrical Topology

            According to the results obtained by simulation, the main tree is an open configuration. The algorithm find 232 alternatives. Among these alternatives, the choice of the optimal solution is made only by closing the switch SW_27-28 in step N° 49 and opening the switches SW_23-26 in step N°78.

            For these alternatives, the minimal cost is represented in table 1 with corresponding power transit. In this work, we represent the merit configuration for this electrical network.

Figure 3. Merit Configuration

Conclusions

            This algorithm differs from most others, by constructing the system from scratch, rather than performing switch exchanges or sequential switch openings. An approximate loss formula helps to quickly screen candidate switch closings, but this method still performs more load flow calculations than other methods. Most of the load flow calculations only work with a subset of the system. The algorithm can solve load either restoration or loss minimization problems. Several test cases show that this algorithm reaches the same optimal solutions found by other investigators. The execution time is not longer, but constraints and control actions are handled more accurately. The work reported here builds on the linearized algorithm. The original contributions of this work, not previously reported, are:

1. The reconfiguration algorithm considers control action and other nonlinear effects during the solution, not after the optimal configuration has been found. This affects both the loss evaluation and the feasible switching operations.

2. Approximate loss formulas were developed in chapter 2 to screen candidate switching operations, making use of partial load flow solutions. After a candidate switch has been selected, the algorithm updates the complete load flow solution. In all test cases evaluated, screening with the approximate loss formulas produced the same solution as screening with full load flow solutions.

3. The heuristic backtracking method presented in this work solving one of the problems encountered in Algerian electrical network.

4. The network load flow solution provides a lower bound on the losses, and a measure of how good the algorithm solution is. This would be a useful addition to other methods, since none can guarantee a global optimum.

The algorithm could include service reliability indices in the merit figure.

Table 1. Optimal solution given by ant colony algorithm

Total Alternatives Number 232	Switches States	Candidate Lines	Topology Cost M$	Power Transit GW
Step N°1: N°49	On	27-28	0.283	10
Step N°1: N°78	Off	23-26	0.331	12.4
Step N°1: N°78	Off	23-26	0.341	12.56

References

1. Colorni A., Dorigo M., Maniezzo V., Distributed Optimization by Ant Colonies, Proceeding of Ecal 91- European Conference on Artificiel Life, Paris, France, Elsevier Publishing, 1991, p. 134–142.

2. Dorigo M., Gambardella L.M., Ant Colony System: A Cooperative Learning Approach to the Traveling Salesman Problem, IEEE Transactions on Evolutionary computation, 1997, 1(1), p. 53-66.

3. Dorigo M., Gambardella L.M., Ant Colonies for the Travelling Salesman Problem. Bio Systems, 1997, 43, p. 73-81.

4. Maniezzo V., Colorni A., The Ant System Applied to the Quadratic Assignment Problem, IEEE Transactions on Knowledge and data Engineering, 1999, 11(5), p 769-778.

5. Maniezzo V., Colorni A., The Ant System Applied to the Quadratic Assignment Problem, IEEE Transactions on Knowledge and data Engineering, 1999, 11(5), p. 769-778.

6. Bauer A., Bullnheimer B., Hartl R.F., Strauss C., Minimizing Total Tardiness on a Single machine using Ant Colony Optimization, Central European Journal of Operations research, 2000, 8(2), p. 125-141.

7. Den Besten M., Stützle T., Dorigo M., Ant Colony Optimization fort he Total Weighted tardiness Problem, Proceeding of the 6^th International Conference on parallel problem Solving from nature (PPSNVI), LNCS 2000, Berlin, p. 611-620.

8. Bullnheimer B., Hartl R. F., Strauss C., Applying the Ant System to the vehicle Routing problem, 2^nd Metaheuristics International Conference (MIC-97), Sophia-Antipolis, France, 1997, p. 21-24.

9. Di Caro G., Dorigo M., Mobile Agents for Adaptive Routing. Proceedings for the 31^st Hawaii International Conference on System Sciences, Big Island of Hawaii, 1998, pp. 74-83.

10. Costa D., Hertz A., Ants Colour Graphs. Journal of the Operational Research Society, 1997, 48, p. 295-305.

11. Schoofs L., Naudts B., Ant Colonies are Good at Solving Contraint Satisfaction Problem, Proceeding of the 2000 Congress on Evolutionary Computation, San Diego, CA, July 2000, p. 1190-1195.

12. Wagner I. A., Bruckstein A. M., Hamiltonian(t)-An Ant inspired heuristic for Recognizing Hamiltonian Graphs, Proceeding of the 1999 Congress on Evolutionary Compuation, Washington, D.C., 1999, p. 1465-1469.

13. Williams B. R., Walden D. G., Distribution Automation Srategy for the Future: Changing the Momentum, IEEE Computer Applications in Power, 1994, 7-3, p. 16-21.

14. Aoki K., Nara K., Itoh M., Satoh T., Kuwabara H., A New Algorithm for Service Restoration in Distribution Systems, IEEE Transactions on Power Delivery, 1989, 4-3, p. 1832–1839.

15. Hayashi Y., Iwamoto S., Furuya S., Liu C.-C., Efficient Determination of Optimal Radial Power System Structure Using Hopfield Neural Network with Constrained Noise, IEEE Transactions on Power Delivery, 1996, 11(3), p. 1529-1535.

16. Dorigo M., Maniezzo V., Colorni A., The Ant System: Optimization by a colony of cooperating agents, IEEE Transactions on Systems, Man and Cybernetics- Part B, 1996, 26(1), p. 1-13.