Investigation into the Thin Layer Drying Models of Nigerian Popcorn Varieties
Taiwo ADEMILUYI, E.O. OBOHO, and Michael OWUDOGU
Department of Chemical/Petrochemical Engineering,
Rivers State University of Science
and Technology, Port Harcourt, Nigeria
E-mail:ademuluyi@yahoo.com
Abstract
Drying kinetics of three popcorn varieties (Pin, Deep and Light yellow) was investigated. The popcorn kernels initially conditioned to 25% moisture content were dried in a bench scale rotary drier to 14% moisture content at various air flow rates (0.83, 1.397, 2.79 m/s) and temperatures (50oC, 60oC, 70oC and 80oC). Falling rate drying period was observed for the three popcorn varieties with Pin popcorn having the highest drying rate. Eight drying models were used to determine the thin layer drying kinetics. The Page equation, Two term model, Modified Page were found the best to describe the thin layer drying of Pin, Light yellow and Deep yellow popcorn, but the newly proposed model serve as a general model which best describe the drying kinetics of all the three popcorn varieties, with high correlation coefficient. The drying behaviour of the three kernels was found to be largely dependent on changes in temperature and air velocity
Keywords
Popcorn varieties, drying kinetics, mathematical models, thin layer
Introduction
The most important factor influencing the economic value of popcorn is popping volume i.e., the volume of popped corn produced from a given weight of unpopped kernels. Processors may reject popcorn that does not meet specified minimum popping volume. Popping volume is affected somewhat by harvesting and handling practices, and by the moisture history of the popcorn prior to popping; but the primary factor is the moisture content of the kernels when popped. Studies have shown that maximum popping volume is produced at moistures ranging from 13.0 to 14.5%, with 13.5% being optimum. Data also indicate that popcorn must be initially dried to at least 13.5% moisture before it attains maximum popping volume. After that, moisture can increase to 15% without significantly decreasing popping volume. Over dried popcorn (11% or below) can be rewetted to 13.5% moisture, but it will not recover the maximum popping volume it had on initial dry down to 13.5%. Popcorn mechanically harvested on the ear at 20-25% moisture content must be dried promptly to prevent mold growth in storage [1]
In Nigeria, popcorn is sun dried below 14% moisture to enable long storage of grain but this creates a lot of work for the processors, as the popcorn has to be rewetted before popping. During this rewetting process the moisture content of the popcorn may be more or less than 14%. Hence it is necessary to understand the drying characteristics of Nigerian popcorn varieties so that they can be conditioned, dried to 14% moisture content and packaged properly like the foreign type before selling to the processor.
Most of the drying studies on popcorn was carried out using thin layer drying models for example Ross and White, 1972; White et al., 1981. and Morel, ,1984 reported that the exponential thin layer model and page was adequate for predicting popcorn drying rates and establishing the effect of drying air conditions on the fully exposed drying characteristics of popcorn. Tran et al (1999) applied the two-compartment model to thin layer drying of two Australian popcorn varieties and obtained a correlation coefficient of 0.9858 and standard error of 0.034, assuming a single linear temperature dependence of the drying constants.
The effect of ethyl oleate on the drying rates for corn was investigated in a pilot plant air-dryer by Doymaz and Mehmet. (2003). Corn was air dried without treatment or after dipping in a cold solution of ethyl oleate. The shorter drying times and best quality dried product were obtained with corn kernels dipped in the solution of ethyl oleate. The single exponential equation and the Page equation were used to determine the thin-layer drying characteristics. Both the equations fitted well to the experimental data. The Page equation was found to better describe the thin-layer drying of corn than the single exponential equation.
Togrul and Pehlivan (2002) developed a mathematical model of solar drying of apricots in thin layer. Drying curves obtained from the data were fitted to 14 mathematical models and the effects of drying air temperature, velocity and relative humidity on the model constants and coefficients were evaluated by the multiple regression and compared to previously given models. The logarithmic drying model was found to satisfactorily describe the solar drying curve of apricots with a correlation coefficient (r) of 0.994.
No work on drying kinetics of Nigerian popcorn varieties was found; hence the objective of this work is to study the thin layer drying characteristics of three Nigerian popcorn varieties. The data obtained would be fitted into 7 generally accepted thin layer drying models and a newly proposed model.
Materials and Methods
Experiment
Popcorn varieties: yellow Pin (rice shaped), Deep yellow, Light yellow (pearl shaped) were obtained from Ahmadu Bello University (ABU), Zaria in Kaduna state, Nigeria. These varieties upon harvesting were sun-dried and stored in bags before they were purchased. These local popcorn varieties upon reception contain about 12.8 – 13.8% moisture. The kernels were cleaned manually to remove all foreign matter and broken kernels. The popcorn kernels were conditioned to 25% moisture content by adding a calculated quantity of water, mixing thoroughly and then sealing in separate polyethylene bags. The samples were kept at 10°C in a refrigerator for 7days for the moisture to distribute uniformly throughout the samples. Before each test, the samples were taken out of refrigerator and allowed to warm up to room temperature. Moisture content of the popcorn kernels was determined with the aid of Delm Horst grain moisture detector (G7) per pass through the rotary dryer.
40g of popcorn sample with 25% moisture content were weighed with electronic balance and dried using a bench scale rotary dryer at drum speed of 12 rev per min. The drying tests were carried out for each popcorn sample at various drying temperature ranging from 50oC, 60oC, 70oC and 80oC and air velocities 0.83, 1.397, and 2.79 m/s. The system was allowed to run till the drying temperature stabilized before the popcorn was charged into the dryer. The samples were allowed to cool in desiccators after each run before final weighing. The drying experiments continued for each sample until the final moisture content of 14% wet basis was obtained.
Thin layer drying models
In drying of thin-layers of agricultural crops, the Page equation has been used extensively. The equation is empirical, and is given in equation (1)[2]
![]() (1)
(1)
where: MR = Moisture ratio; Mo = initial moisture content (% db); Me = equilibrium moisture content (% db); M = moisture content at time t (% db); t = drying time (hr); k and n = drying constants.
Moisture ratio data obtained at air temperatures of 50 - 80oC for each variety were fitted into 7 generally accepted drying models and a newly proposed model (Taiwo Modified Page model), as shown in Table 1. Regression analyses were done using the Datafit 8.2 (Oakdale Engineering statistical software, USA). The coefficient of correlation (r) was one of the primary criteria for selecting the best equation to define the thin layer drying curves of each popcorn variety. Equilibrium moisture content (Me) of 14% (dry basis) was used; this value has been accepted as the final moisture for packaging these varieties before popping [3].
Table 1: Mathematical models given by various authors for the drying curves
|
Model No. |
Name |
Model equation |
References |
|
1 |
Newton |
MR= exp(-kt) |
[4] |
|
2 |
Page |
MR = exp(-ktn) |
[5] |
|
3 |
Modified Page |
MR = exp(-(kt)n) |
[6] |
|
4 |
Henderson and Pabis |
MR = a∙exp(-kt) |
[7] |
|
5 |
Logarithmic |
MR = a∙exp(-kt) + c |
[8] |
|
6 |
Two-term |
MR= a∙exp(-kot) + b∙exp (-k1t) |
[9] |
|
7 |
Wang and Singh |
MR = 1 + at + bt2 |
[10] |
|
8 |
Newly proposed model |
MR = a∙exp(-(kt)n) |
[11] |
Results and Discussion
Effect of Moisture Content and Drying Time on Drying Rates.
The variations of drying rate with moisture for the three popcorn varieties are shown in Figs 1 and 2. Drying rate decreases for all the samples with decrease in moisture content. Falling rate drying period was exhibited by the varieties. This means that the movement of water is basically diffusion controlled as reported by McCabe et al, (1987).
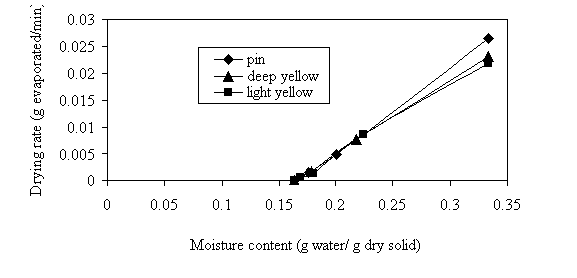
Figure 1. Rate of drying curve for different popcorn varieties at 70°C, 12 rev/min, 1.397m/s

Figure 2. The changes with time of the drying rate of popcorn varieties at 70°C, 12 rev/min, 1.397m/s
The moisture content decreases with drying time for all the varieties, but the drying times of each kernel samples were not the same. This same behaviour was exhibited during the drying of apricot [12] and Australian popcorn varieties [13]
Pin popcorn had the shortest drying time (19 mins) while light yellow popcorn has a longer drying time of 30 mins, to reach a final moisture of 14% wet basis as shown in Fig. 3.

Figure 3. Drying curve of different popcorn at 70oC, 12 rev/min, 1.397m/s
Effect of Air Flow Rates and the Temperature on the Drying Rates
From Figs 4 - 6, the moisture content decreases as temperature increases for all the varieties. The drying rate also increases with temperature. Pin popcorn dried faster than deep yellow and light yellow popcorn at all temperatures (i.e. 50oC, 60oC, 70oC and 80oC). The porosity of the varieties reported by Taiwo et al., (2006), revealed that Pin popcorn had a porosity of 42.88% while Light and Deep yellow had 38.80% and 31.50% respectively. Pin popcorn seems to be more porous hence moisture will be released faster from its pores than other varieties.
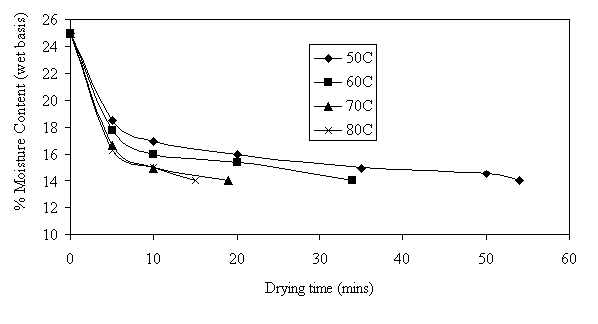
Fig 4. Drying Curve for Pin Popcorn at different temperatures.
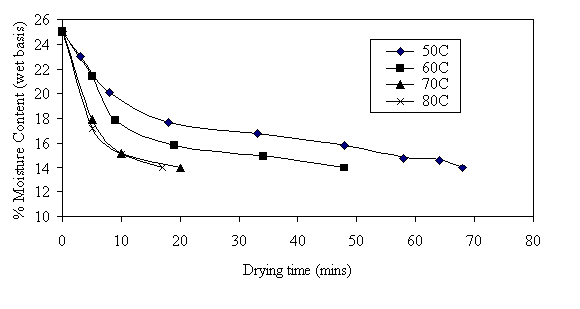
Figure 5. Drying curve for deep yellow popcorn at different temperatures.
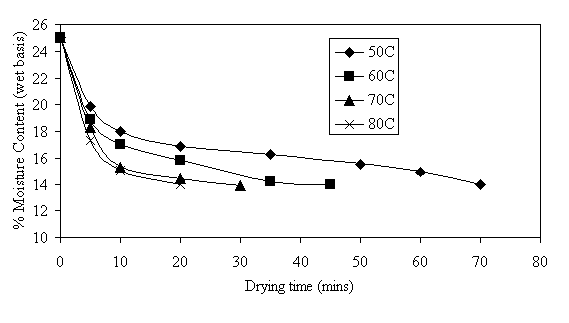
Figure 6. Drying Curve for Light Yellow Popcorn at different temperatures.
At different air velocities, the moisture content also decreased with time as the air velocity increased as shown in Fig 7. The changes occurring in the moisture content of popcorn by varying the air flow rates at constant air temperature seem more pronounced than those observed by varying the air temperatures at constant air flow rates. This dominance of air flow rates over the temperature is related to the transport of water vapour to the main air stream. Increasing airflow rates reduces the thickness of the boundary layer between airflows and the surface of the popcorn kernels. A similar behaviour was reported for apricot and fruit drying [12]
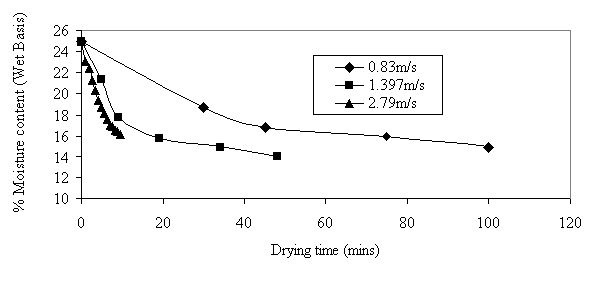
Figure 7. Effect of air velocity on the drying behaviour of Deep yellow popcorn
Modeling of Drying Curve
The falling rate drying behaviour exhibited by the popcorn varieties reveals that the Newly proposed model and other acceptable general drying models listed in the Table 1 can be used to model the drying curve for the three popcorn varieties. The experimental results were used to calculate the moisture ratio. Equilibrium moisture content of 14% was used in the calculation because this is the best moisture content popcorn can be dried before packaging. The highest popping volume is obtained at this moisture content as stated earlier. From Figs 8 - 10, the moisture ratio decreased as temperature increases and approaches zero as it reaches the equilibrium moisture content. Tran et al, 1999 reported a similar result for Australian popcorn.
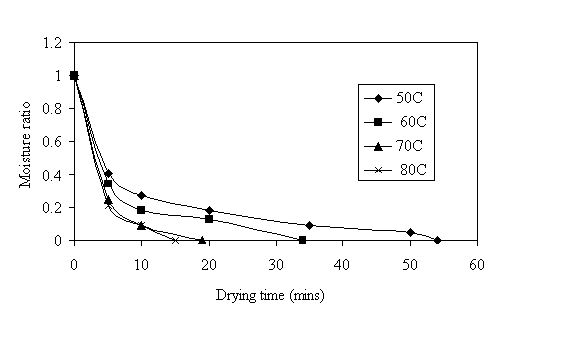
Figure 8. Moisture ratio versus drying time for Pin popcorn
Table 2- 4 shows the regression analysis of the experimental results for the popcorn varieties using eight models. The model results (Table 2) from regression analysis of the experimental data for Pin popcorn showed that the drying behaviour of Pin popcorn can be modeled with Two term, Page, modified Page or the newly proposed model with a coefficient of multiple determination of 0.996.
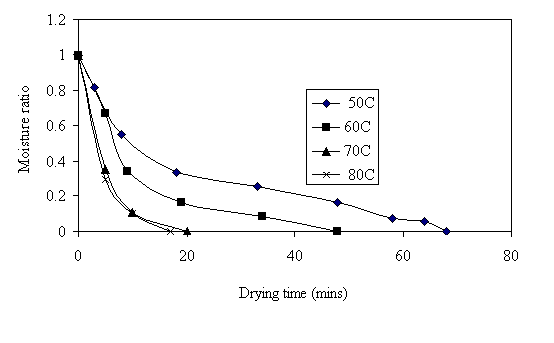
Figure 9. Moisture ratio versus drying time for Deep yellow popcorn
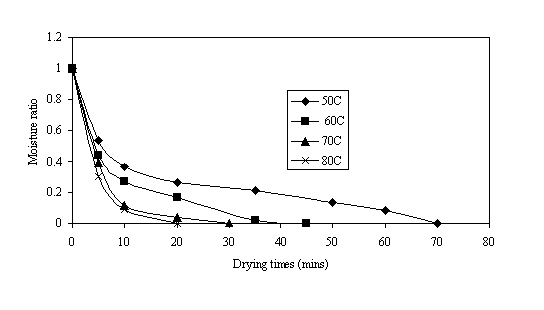
Figure 10. Moisture ratio versus drying time for Light yellow popcorn
Moisture ratio obtained from experiment, Page model and Newly proposed model for Pin popcorn is presented in Fig 11. Doymaz & Mehmet [14], obtained similar result for corn. Wang and Singh model has the least r2. The logarithmic model was not applicable for predicting the drying behaviour of the popcorn varieties. The results were obtained using moisture content results of four passes through the rotary dryer for good comparison between popcorn varieties.
The result from Table 3 also revealed that the drying kinetics of Deep yellow popcorn could best be modeled using the Two term model, the newly proposed model modified Page and Page models. Newton, Henderson and Pabis and Logarithmic model were not applicable
Light yellow popcorn can also be modeled from the result in Table 4 using Two term, Page, modified Page and the newly proposed model. The drying kinetics of Pin, Deep and Light yellow popcorn fitted best into the newly proposed model as shown in Fig 12 and 13. Tran et al. (1999), reported a high correlation coefficient r2 of 0.995 for two-compartment model for two Australian popcorn varieties
Table 2. Results of statistical analyses on the modelling of moisture contents and drying time for Pin popcorn at 60oC
|
Models |
Model coefficients |
Coefficient values |
95% Confidence intervals |
SEE |
RSS |
R2 |
|
|
Lower Limit |
Upper Limit |
||||||
|
Two term |
a |
0.670177 |
-3.38835 |
4.728701 |
0.045358 |
0.002057 |
0.996755 |
|
b |
4.33E-01 |
-4.24758 |
5.114269 |
|
|
|
|
|
c |
0.329983 |
-3.69297 |
4.352933 |
|
|
|
|
|
d |
7.02E-02 |
-0.66411 |
0.804435 |
|
|
|
|
|
Newly proposed model |
a |
0.999972 |
0.847076 |
1.152868 |
0.035539 |
0.002526 |
0.996016 |
|
k |
0.266182 |
2.18E-02 |
0.510579 |
|
|
|
|
|
n |
0.566252 |
0.052698 |
1.079807 |
|
|
|
|
|
Modified page |
k |
0.266194 |
0.124217 |
0.408172 |
0.029017 |
0.002526 |
0.996016 |
|
n |
0.566243 |
0.257597 |
0.874889 |
|
|
|
|
|
Page |
k |
0.472632 |
0.152607 |
0.792656 |
0.029017 |
0.002526 |
0.996016 |
|
n |
0.566243 |
0.257597 |
0.874889 |
|
|
|
|
|
Herderson and pabis |
a |
0.991148 |
0.790299 |
1.191997 |
0.063492 |
0.012094 |
0.980924 |
|
k |
0.206459 |
0.108437 |
0.304482 |
|
|
|
|
|
Newton |
k |
0.208154 |
0.138046 |
0.278262 |
0.055162 |
0.012171 |
0.980802 |
|
Wang and Singh |
a |
-9.46E-02 |
-0.15361 |
-3.56E-02 |
0.20709 |
0.128659 |
0.797065 |
|
b |
1.97E-03 |
-1.97E-06 |
3.94E-03 |
|
|
|
|
Where, SEE is the standard error of estimate, RSS is the residual sum of squares and R2 is the correlation coefficient of multiple determinations.
Table 3. Results of statistical analyses on the modelling of moisture contents and drying time for Deep yellow popcorn at 60oC
|
Models |
Model coefficient |
Coefficient values |
95% Confidence intervals |
SEE |
RSS |
R2 |
|
|
Lower Limit |
Upper Limit |
||||||
|
Two term |
a |
1.011601 |
-5.50E-02 |
2.078165 |
0.083243 |
0.006929 |
0.988286 |
|
b |
1.11E-01 |
-0.31408 |
0.536158 |
|
|
|
|
|
c |
1.35E-03 |
-0.52665 |
0.529348 |
|
|
|
|
|
d |
-1.05E-01 |
-11.5428 |
11.33199 |
|
|
|
|
|
Newly proposed model |
a |
1.007144 |
0.717418 |
1.29687 |
0.067525 |
0.009119 |
0.984584 |
|
k |
0.107482 |
4.25E-02 |
0.172481 |
|
|
|
|
|
n |
1.014991 |
-7.76E-03 |
2.037742 |
|
|
|
|
|
Modified page |
k |
0.106649 |
7.36E-02 |
0.139736 |
0.055292 |
0.009172 |
0.984495 |
|
n |
1.021426 |
0.421717 |
1.621134 |
|
|
|
|
|
Page |
k |
0.101655 |
-3.72E-02 |
0.24048 |
0.055292 |
0.009172 |
0.984495 |
|
n |
1.021426 |
0.421717 |
1.621135 |
|
|
|
|
|
Wang and Singh |
a |
-7.81E-02 |
-1.00E-01 |
-5.60E-02 |
0.076864 |
0.017724 |
z0.970037 |
|
b |
1.51E-03 |
7.78E-04 |
2.24E-03 |
|
|
|
|
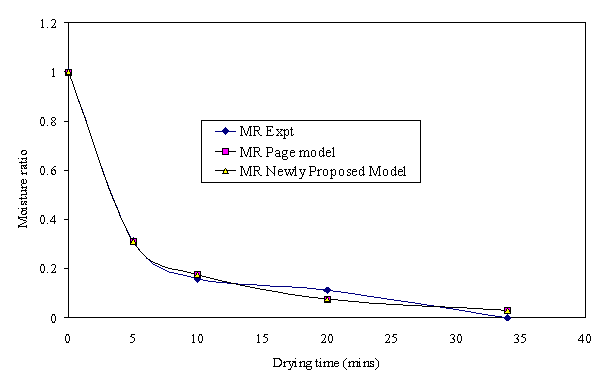
Figure 11 Moisture ratio experiment, Page model and Newly proposed model for Pin popcorn
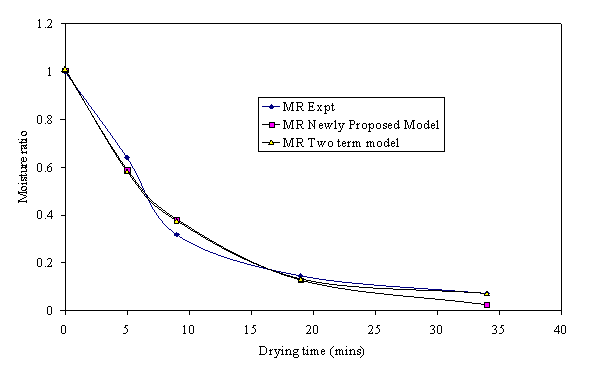
Figure 12. Moisture ratio experiment, two term model and newly proposed model for deep yellow popcorn
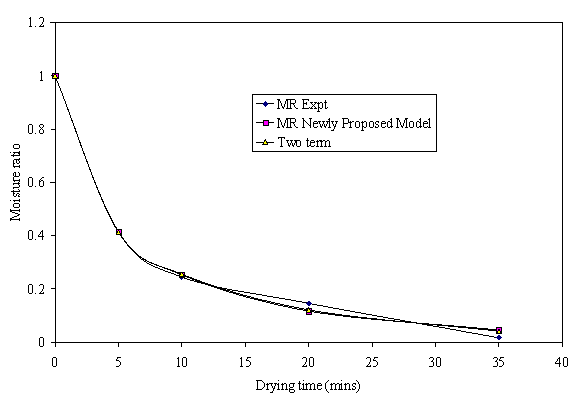
Figure 13. Moisture ratio experiment, two term model and Newly proposed model for Light yellow popcorn
Table 4 Results of Statistical Analyses on the Modeling of Moisture Contents and Drying Time For Light Yellow Popcorn at 60oC
|
Models |
Model coefficient |
Coefficient values |
95% Confidence intervals |
SEE |
RSS |
R2 |
|
|
Lower Limit |
Upper Limit |
||||||
|
Two term |
a |
0.491111 |
-2.85707 |
3.839295 |
0.036145 |
0.001306 |
0.997783 |
|
|
b |
4.32E-01 |
-4.7131 |
5.577337 |
|
|
|
|
|
c |
0.509018 |
-2.81195 |
3.829983 |
|
|
|
|
|
d |
7.15E-02 |
-0.32498 |
0.4679 |
|
|
|
|
Newly proposed model |
a |
0.999679 |
0.872151 |
1.127206 |
0.029651 |
0.001758 |
0.997016 |
|
k |
0.163397 |
8.81E-02 |
0.238732 |
|
|
|
|
|
n |
0.644421 |
0.277609 |
1.011233 |
|
|
|
|
|
Modified page |
k |
0.16348 |
8.82E-02 |
0.238738 |
0.024211 |
0.001758 |
0.997015 |
|
n |
0.644274 |
0.243082 |
1.045465 |
|
|
|
|
|
Page |
k |
0.311355 |
0.15385 |
0.468859 |
0.024211 |
0.001758 |
0.997015 |
|
|
n |
0.644274 |
0.425685 |
0.862862 |
|
|
|
|
Wang and Singh |
a |
-8.38E-02 |
-1.29E-01 |
-0.03847 |
0.163531 |
0.080227 |
0.863834 |
|
|
b |
1.63E-03 |
1.62E-04 |
3.09E-03 |
|
|
|
The newly proposed model (Taiwo Modified Page model) could be used as a general model to predict the drying kinetics for all the popcorn varieties, with high correlation coefficient. (r2 ~ 1) for all the cultivars as shown in Tables. 2, 3 and 4. Also it has a lower standard error of estimate (SEE) than the Two term model.
In general using the newly proposed model the moisture ratio can be modeled with time for the popcorn varieties as
1. Pin popcorn: M =0.999exp (-0.266t0.566), r2=0.996, error = 0.0355
2. Deep yellow popcorn MR=1.007exp (-0.108t1.015), r2 =0.985, error =0.0675
3. Light yellow popcorn MR=0.999exp (-0.163t0.644), r2 = 0.997, error = 0.0297
Comparing the value of the drying constants k (which ranged from 0.266 to 0.108 for all the popcorn varieties) in the newly proposed model showed that the drying constants (k) are different for all the popcorn varieties with different drying kinetics.
Conclusion
Falling rate period was exhibited by the three popcorn varieties at different temperatures and airflow velocities. Hence, the moisture movements in the kernels are diffusion controlled. The three popcorn varieties when dried at the same condition had different drying time. The page equation was found best to describe the thin layer drying of Pin popcorn while the two term model was found to best describe the thin layer drying of Deep and light yellow popcorn. The Page equation, Two term model, Modified Page were found the best to describe the thin layer drying of Pin, Light yellow and Deep yellow popcorn, but the newly proposed model serve as a general model which best describe the drying kinetics of all the three popcorn varieties, with high correlation coefficient. The Nigerian popcorn varieties thus have different drying characteristics. Due to the large dependence of the drying rate on the temperature and the air velocity for all the varieties, work is in progress to study the effect of changing other drying parameters like, drum speed, feed flow rate as well as air humidity on the drying constants of the three popcorn varieties obtained from this research. These data would therefore be useful in the design of dryers for Nigerian popcorn varieties after proper conditioning and would further lead to processing and packaging of these varieties for export.
References
1. Carter P.R., Hicks D.R., Doll J.D, Schulte E.E., Schuler R., & Holmes B. (1989) Popcorn: Alternative field crop manual URL: http://www.hort.purdue.edu/newcrop/afcm/ popcorn html August 6, 2006.
2. Togrul I. T & Pehlivan D .Mathematical modeling of solar drying of apricots in thin layers. Journal of Food Engineering 55, 209–216, 2002.
3. Gokmen S. Effects of moisture content and popping method on popping characteristics of popcorn Journal of Food Engineering. 65 (3):357-362,2004.
4. Liu, Q., & Bakker-Arkema, F. W. Stochastic modelling of grain drying, Part 2: Model development. Journal of Agricultural Engineering Research, 66, 275–280, 1997.
5. Agrawal, Y. C., & Singh, R. P. Thin layer drying studies on short grain rough rice. ASAE Paper No: 3531,1977.
6. White, G. M., Ross, I. J., & Ponelert, C.G. Fully exposed drying of popcorn. Transactions of the ASAE, 24, 466–468,1981b.
7. Chhninman, M. SEvaluation of selected mathematical models for describing thin layer drying of in-shell pecans. Transactions of the ASAE, 27, 610–615, 1984.
8. Yagcıoglu, A., Degirmencioglu, A., & Cagatay, F. Drying characteristic of laurel leaves under different conditions. In A. Bascetincelik (Ed.), Proceedings of the 7th International Congress on Agricultural Mechanization and Energy, 26–27, 1999.
9. Rahman, M. S., Perera, C. O., & Theband, C. Desorption isotherm and heat pump drying kinetics of peas. Food Research International, 30, 485–491, 1998.
10. Wang, C. Y., & Singh, R. P. A single layer drying equation for rough rice. ASAE Paper No: 3001, 1978.
11. Ademiluyi Taiwo. Development of predictive models for drying fermented ground cassava, Unpublished PhD Thesis in Chemical Engineering River State university of Science and Technology, 2008.
12. Togrul I. T & Pehlivan D .Modelling of drying kinetics of single apricots . Journal of Food Engineering 58: 23 – 32, 2003.
13. Tran T.T, Srzednicki G. S &. Driscoll R.H Effects of Aeration on the Quality of popcorn. Vol. I, December, 1999.
14. Doymaz I & Mehmet. P. Thin layer drying characteristics of corn. Journal of Food Engineering. 60 (2): 125 – 130, 2003.