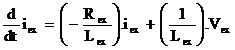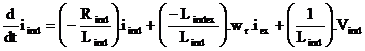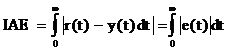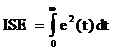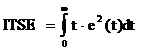Setting Up PID DC Motor Speed Control Alteration Parameters Using Particle Swarm Optimization Strategy
Boumediène ALLAOUA*, Brahim GASBAOUI and Brahim MEBARKI
Bechar University, Faculty of Sciences and Technology, Department of Electrical Engineering,
B.P 417 BECHAR (08000) Algeria
E-mail(s): elec_allaoua2bf@yahoo.fr, gasbaoui_2009@yahoo.com, brahimo12002@yahoo.fr
(*Corresponding Author)
Abstract
In this paper, an intelligent controller of DC Motor drive is designed using particle swarm optimization (PSO) method for formative the optimal proportional-integral-derivative (PID) controller Tuning parameters. The proposed approach has superior feature, including easy implementation, stable convergence characteristics and very good computational performances efficiency. The DC Motor Scheduling PID-PSO controller is modeled in MATLAB environment. Comparing with fuzzy logic controller using PSO intelligent algorithms, the planned method is more proficient in improving the speed loop response stability, the steady state error is reduced, the rising time is perfected and the disturbances do not affect the performances of driving motor with no overtaking.
Keywords
Control Tuning Parameters; Particle Swarm Optimization Strategy; Scheduling PID-PSO Controller; DC Motor Speed Control; Optimal Control.
Introduction
In spite of the development of power electronics resources, the direct current machines are becoming more and more useful insofar as they have found wide application, i.e. automobile industry (electric vehicle), weak power using battery system (motor of toy), the electric traction in the multi-machine systems, etc.
The speed of DC motor can be adjusted to a great extent so as to provide easy control and high performance [1, 2]. There are several conventional and numeric controller types intended for controling the DC motor speed at its executing various tasks: PID Controller, Fuzzy Logic Controller; or the combination between them: PID-Particle Swarm Optimization, PID-Neural Networks, PID-Genetic Algorithm, PID-Ants Colony Optimization and the optimal Fuzzy Logic controller using the different strategy.
PID controllers are widely used in industrial plants because it is simple and robust. Industrial processes are subjected to variation in parameters and parameter perturbations, which when significant makes the system unstable. So the control engineers are on look for automatic tuning procedures.
From the control point of view, dc motor exhibit excellent control characteristics because of the decoupled nature of the field [2]. Recently, many modern control methodologies such as nonlinear control [3], optimal control [4], variable structure control [5] and adaptive control [6] have been extensively proposed for DC motor. However, these approaches are either complex in theorical bases or difficult to implement [7]. PID control with its three term functionality covering treatment to both transient and steady-states response, offers the simplest and yet most efficient solution too many real world control problems [8]. In spite of the simple structure and robustness of this method, optimally tuning gains of PID controllers have been quite difficult.
The PSO methods have been employed successfully to solve complex optimization problems. PSO first introduced by Kennedy and Eberhart [9] is one of the modern heuristic algorithms; it has been motivated by the behavior of organisms, such as fish schooling and bird flocking [10, 11]. Generally, PSO is characterized as a simple concept, easy to implement, and computationally efficient. Unlike the other heuristic techniques, PSO has a flexible and well-balanced mechanism to enhance the global and local exploration abilities [12].
In this paper, a scheduling PID tuning parameters using particle swarm optimization strategy for a DC motor speed control is proposed. This paper has been organized as follows: in section 2 the DC motor is described and the model of it is shown. In section 3, the particle swarm optimization method is reviewed. Section 4, describes how PSO is used to design the PID controller values optimally for a DC motor speed control. A comparison between the results obtained by the proposed method and Fuzzy-PSO method [13] via simulation the DC motor speed control is presented in section 5. The paper is concluded in section 6.
Model of DC motor
DC machines are characterized by their versatility. By means of various combinations of shunt-, series-, and separately-excited field windings they can be designed to display a wide variety of volt-ampere or speed-torque characteristics for both dynamic and steady-state operation. Because of the ease with which they can be controlled systems of DC machines have been frequently used in many applications requiring a wide range of motor speeds and a precise output motor control [14, 15].
In this paper, the separated excitation DC motor model is chosen according to his good electrical and mechanical performances more than other DC motor models. The DC motor is driven by applied voltage. Fig.1 show the equivalent circuit of DC motor with separate excitation. The characteristic equations of the DC motor are represented as:
|
|
(1) |
|
|
(2) |
|
|
(3) |
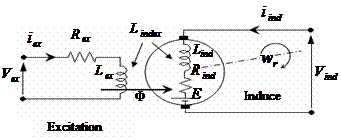
Figure 1. Equivalent circuit of DC motor with Separate Excitation
The equivalent circuit of DC motor with separate excitation illustrated in Fig. 1.
Table 1. Used symbols
|
Symbols |
Designations |
Units |
|
|
Excitation current and Induced current. |
[A] |
|
|
Rotational speed of the DC Motor. |
[Rad/Sec] |
|
|
Excitation voltage and Induced voltage |
[Volt] |
|
|
Excitation Resistance and Induced Resistance. |
[W] |
|
|
Excitation Inductance, Induced Inductance and Mutual Inductance. |
[mH] |
|
|
Moment of Inertia. |
[Kg.m2] |
|
|
Couple resisting. |
[N.m] |
|
|
Coefficient of Friction. |
[N.m.Sec/Rad] |
From the state equations (1), (2), (3) previous, can construct the model with the environment MATLAB 7.4 (R2007a) in Simulink version 6.6. The model of the DC motor in Simulink is shown in Fig. 2. The various parameters of the DC motor are shown in Table 2.
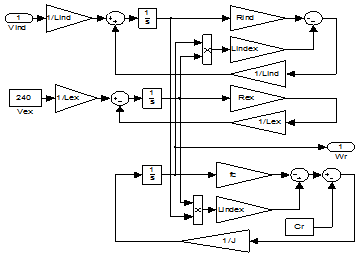
Figure 2. Model of the DC Motor in Simulink
Table 2. Parameters of the DC Motor
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Overview Particle Swarm Optimization
PSO is a population-based optimization method first proposed by Eberhart and Colleagues [9, 10, 11]. Some of the attractive features of PSO include the ease of implementation and the fact that no gradient information is required. It can be used to solve a wide array of different optimization problems. Like evolutionary algorithms, PSO technique conducts search using a population of particles, corresponding to individuals. Each particle represents a candidate solution to the problem at hand. In a PSO system, particles change their positions by flying around in a multidimensional search space until computational limitations are exceeded. Concept of modification of a searching point by PSO is shown in Fig. 3.
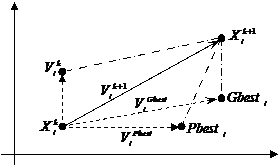 Xk : current position,
Xk : current position,
Xk+1 : modified position,
Vk : current velocity,
Vk+1 : modified velocity,
VPbest : velocity based on Pbest,
VGbest : velocity based on Gbest.
Figure 3. Concept of modification of a searching point by PSO
The PSO technique is an evolutionary computation technique, but it differs from other well-known evolutionary computation algorithms such as the genetic algorithms. Although a population is used for searching the search space, there are no operators inspired by the human DNA procedures applied on the population. Instead, in PSO, the population dynamics simulates a ‘bird flock’s’ behavior, where social sharing of information takes place and individuals can profit from the discoveries and previous experience of all the other companions during the search for food. Thus, each companion, called particle, in the population, which is called swarm, is assumed to ‘fly’ over the search space in order to find promising regions of the landscape. For example, in the minimization case, such regions possess lower function values than other, visited previously. In this context, each particle is treated as a point in a d-dimensional space, which adjusts its own ‘flying’ according to its flying experience as well as the flying experience of other particles (companions). In PSO, a particle is defined as a moving point in hyperspace. For each particle, at the current time step, a record is kept of the position, velocity, and the best position found in the search space so far.
The assumption is a basic concept of PSO [9]. In the PSO algorithm, instead of using evolutionary operators such as mutation and crossover, to manipulate algorithms, for a d-variable optimization problem, a flock of particles are put into the d-dimensional search space with randomly chosen velocities and positions knowing their best values so far (Pbest) and the position in the d-dimensional space. The velocity of each particle, adjusted according to its own flying experience and the other particle’s flying experience. For example, the i-th particle is represented as xi = (xi,1 ,xi,2 ,…, xi,d) in the d-dimensional space. The best previous position of the i-th particle is recorded and represented as:
|
Pbesti = (Pbesti,1, Pbesti,2 ,..., Pbest i,d) |
(4) |
The index of best particle among all of the particles in the group is gbestd. The velocity for particle i is represented as vi = (vi,1 ,vi,2 ,…, vi,d). The modified velocity and position of each particle can be calculated using the current velocity and the distance from Pbesti,d to gbestd as shown in the following formulas [9, 10, 11]:
|
|
(5) |
|
|
(6) |
where:
N Number of particles in the group,
d dimension,
t Pointer of iterations(generations),
![]() Velocity
of particle I at iteration t,
Velocity
of particle I at iteration t, ![]()
w Inertia weight factor,
c1,c2 Acceleration constant,rand() Random number between 0 and 1, Rand()
![]() Current position of particle i at
iterations,
Current position of particle i at
iterations,
Pbesti Best previous position of the i-th particle, gbest Best particle among all the particles in the population.
Realization of a PID-PSO Controller Tuning Optimal Parameters
Fitness Function
The general equation of PID controller is [8]:
|
|
(7) |
where: Kp = proportional gain; Ti = integral time; Td= derivative time.
The variable e(t) represents the tracking error which is the difference between the desired input value and the actual output. This error signal will be sent to the PID controller and the controller computes both the derivative and the integral of this error signal.
The signal U(t) from the controller is now equal to the proportional gain (Kp) times the magnitude of the error plus the integral gain (Ki) times the integral of the error plus the derivative gain (Kd) times the derivative of the error [8, 18].
In PID controller design methods, the most common performance criteria are integrated absolute error (IAE), the integrated of time weight square error (ITSE) and integrated of squared error (ISE) that can be evaluated analytically in the frequency domain [16, 18]. These three integral performance criteria in the frequency domain have their own advantage and disadvantages. For example, disadvantage of the IAE and ISE criteria is that its minimization can result in a response with relatively small overshoot but a long settling time because the ISE performance criterion weights all errors equally independent of time. Although the ITSE performance criterion can overcome the disadvantage of the ISE criterion, the derivation processes of the analytical formula are complex and time-consuming [16, 17]. The IAE, ISE, and ITSE performance criterion formulas are as follows:
|
|
(8) |
|
|
(9) |
|
|
(10) |
In this paper a time domain criterion is used for evaluating the PID controller. A set of good control parameters P, I and D can yield a good step response that will result in performance criteria minimization in the time domain. These performance criteria in the time domain include the overshoot, rise time, settling time, and steady-state error.
Scheduling PSO for PID Controller parameters
In this paper, An PID controller used PSO Algorithms to find the optimal parameters of DC Motor speed control system. The structure of the PID controller with PSO algorithms is shown in Fig. 4.
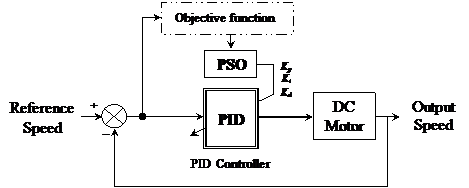
Figure 4. The block diagram of proposed PID Controller with PSO algorithms
The control system performs poor in characteristics and even it becomes unstable, if improper values of the controller tuning constants are used. So it becomes necessary to tune the controller parameters to achieve good control performance with the proper choice of tuning constants [19, 20].
Unlike the conventional techniques, wherein the particles having unfavorable costs are discarded and those with favorable costs are reproduced, the unification of particle clusters allows us to use the same position in the optimal solution space.
The ith particle other than the best one is made to assume different positions on the surface of the virtual sphere centered at the i th particle position, whose radius is the Euclidean distance between this and the best particle. Every time, as the particles assume new positions, it is ensured to update the best particle by comparing the costs corresponding to these positions with the previously selected best particle cost. [21]
Simultaneously, the best particle in a given instant is assumed to ‘diffuse attractant’ towards the rest of the particles in the cluster, which leads to establishment of ‘cones of attraction’ with axes connecting the best particle and the rest in the population. Subject to the condition that the angle subtended by the vector joining the ith particle to the best one and the vector joining the present and the next positions of the ith particle lies within new degrees.
In the proposed PSO method each particle contains three members P, I and D. It means that the search space has three dimension and particles must ‘fly’ in a three dimensional space. The flowchart of the PSO-PID control system is shown in Fig. 5.

Figure 5. The flowchart of the PSO-PID control system
Objectives:
Ú Our objective here is to minimize the error.
Ú We calculate the step response of the system and out of which we calculate the error.
Ú The Iterations are run till the error minimizes.
Computer Simulation Results
Optimal PID-PSO Controller Response
To control the speed of the DC motor at 127.93 Rad/Sec, according to the trials, the following PSO parameters (table 3) are used to verify the performance of the PID-PSO controller parameters.
Table 3. Parameters of PSO algorithms
|
Population Size |
20 |
|
Number of Iterations |
300 |
|
wmax |
0.6 |
|
wmin |
0.1 |
|
c1 = c2 |
1.5 |
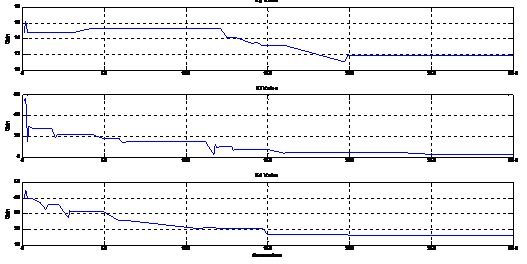
Figure 6. Illustration of PSO Algorithms converging through
The simulation results are obtained for 0.01 second range time. The best population may be plotted to give an insight into how the PSO Algorithm converged to its final values as illustrated in Fig 6. The speed response of PID Controller tuning parameters using particle swarm optimization strategy is shown in Fig 7. Table 4 lists the performance of PID-PSO controller. Particle swarm optimization Algorithm values : Kp = 11.88466 ; Ki = 3.47410 ; Kd = 16.23086.
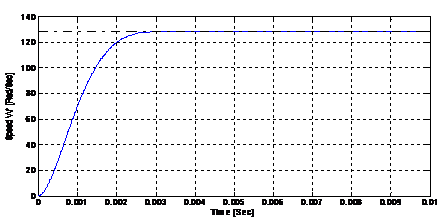
Figure 7. The speed response of PID Controller tuning parameters using PSO strategy
Table 4. Performance of PID-PSO controller
|
[ Kp ; Ki ; Kd ] |
[11.88466; 3.47410; 16.23086] |
|
Rising time [Sec] |
0.00285 |
|
Overtaking [%] |
0 |
|
Steady state error [%] |
0 |
Results Comparison of PID-PSO Controller with Fuzzy-PSO Controller
To show the effectiveness of the proposed approach, a comparison is made with the designed PID controller using PSO and Fuzzy controller optimized via PSO [13]. The performances of the Fuzzy-PSO controller are listed in Table 5.
Table 5. Performance of Fuzzy-PSO controller
|
Results |
Fuzzy-PSO Controller [13] |
|
Rising time [Sec] |
0.0087 |
|
Overtaking [%] |
0 |
|
Steady state error [%] |
0 |
Table 6: Performances of the two controllers
|
Results |
Fuzzy-PSO Controller [13] |
PID-PSO Controller |
|
Rising time [Sec] |
0.0087 |
0.00285 |
|
Overtaking [%] |
0 |
0 |
|
Steady state error [%] |
0 |
0 |
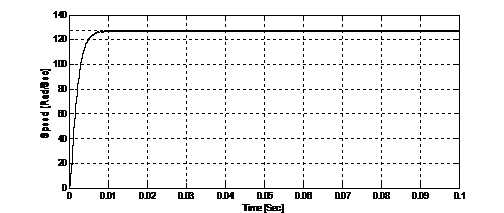
Figure 8. The speed response of PID-PSO Controller and Fuzzy-PSO Controller
The speed response of PID-PSO Controller comparing with the speed response of FLC (Fuzzy Logic Controller) with PSO algorithms is shown in Fig 8. Table 6 lists the performances of the two controllers.
Conclusions
In this paper a new design method to determine optimal PID controller parameters using the PSO method is presented. The speed of a DC Motor drive is controlled by PID-PSO controller. Obtained through simulation of DC motor; the results show that the proposed controller can perform an efficient search for the optimal PID controller. By comparison with Fuzzy-PSO controller, it shows that this method can improve the dynamic performance of the system in a better way. The PID-PSO controller is the best which presented satisfactory performances and possesses good robustness (no overshoot, minimal rise time, Steady state error = 0).
References
1. Hénao H., Capolino G. A., Méthodologie et application du diagnostic pour les systèmes électriques, Article invité dans Revue de l'Electricité et de l'Electronique (REE), No. 6, (in French), Jun. 2002, p. 79 – 86.
2. Raghavan S., Digital Control for Speed and Position of a DC Motor, MS Thesis, Texas A&M University, Kingsville, Aug. 2005.
3. Weerasooriya S., El-Sharkawi M. A., Identification and control of a DC motor using back propagation neural networks, IEEE Trans. Energy Conversion, Vol. 6, p. 663 – 669, 1991.
4. Reyer J. A., Papalambros P. Y., An Investigation into Modeling and Solution Strategies for Optimal Design and Control, ASME Design Engineering Technical Conferences, Las Vegas, Nevada, Sep, p. 10 – 13, 2000.
5. Lin F. J., Shyu K. K., Lin Y. S., Variable structure adaptive control for PM synchronous servo motor drive, IEE Proc. IEE B: Elect. Power Applicat., vol. 146, Mar., p. 173 – 185, 1999.
6. Rubaai A., Kotaru R., Online identification and control of a DC motor using learning adaptation of neural networks, IEEE Trans. Industry Application, Vol. 36, p. 935 – 942, 2000.
7. Lin C. L., Jan H. Y., Evolutionarily multi-objective PID control for linear brushless DC motor, in Proc, IEEE Int. Conf .Industrial Elect. Society, Nov., p. 39 – 45, 2002.
8. Ang K., Chong G., Li Y., PID control system analysis, design, and technology, IEEE Trans. Control System Technology, vol. 13, p. 559 – 576, Jul. 2005.
9. Kennedy J., Eberhart R., Particle swarm optimization, Proc. IEEE Int. Conf. on Neural Network, Vol. 4, p. 1942 – 1948, 1995.
10. Shi Y., Eberhart R., A modified particle swarm optimizer, Proc. 1998 Int. Conf. on Evolutionary Computation, The IEEE World Congress on Computational Intelligence, Anchorage, May 1998, p. 69 – 73.
11. Clerc M., Kennedy J., The particle swarm-explosion, stability, and convergence in a multidimensional complex space, IEEE Trans. Evolutionary Computation, 2002, Vol. 6, p. 58 –73.
12. Abido M. A., Optimal design of power-system stabilizers using particle swarm optimization, IEEE Trans. Energy Conversion, Sep. 2002, vol. 17, p. 406 – 413.
13. Allaoua B., Abderrahmani A., Gasbaoui B., Nasri A., The Efficiency of Particle Swarm Optimization Applied on Fuzzy Logic DC Motor Speed Control, SERBIAN JOURNAL OF ELECTRICAL ENGINEERING, Vol. 5, No. 2, Nov. 2008, p. 247 – 262.
14. Halila A., Étude des machines à courant continu, MS Thesis, University of LAVAL, (in French), May 2001.
15. Capolino G.A., Cirrincione G., Cirrincione M., Henao H., Grisel R., Digital Signal Processing for Electrical Machines, Invited paper, Proceedings of ACEMP'01 (Aegan International Conference on Electrical Machines and Power Electronics), Kusadasi, Turkey, June 2001, p. 211 – 219.
16. Lieslehto J., PID controller tuning using Evolutionary programming, American Control Conference, VA June 25-27, 2001.
17. Mitsukura Y., Yamamoto T., Kaneda M., A design of self-tuning PID controllers using a genetic algorithm, in Proc. Amer. Contr. Conf., San Diego, CA, June 1999, p. 1361 – 1365.
18. Popov A., Farag A., Werner H., Tuning of a PID controller Using a Multi-objective Optimization Technique Applied to A Neutralization Plant, 44th IEEE Conference on Decision and Control, and the European Control Conference 2005.
19. Gaing Z. L., A particle swarm optimization approach for optimum design of PID controller in AVR system, IEEE Trans. Energy Conversion, vol. 19, June 2004, p. 384 – 391.
20. Kim T. H., Maruta I., Sugie T., Robust PID controller tuning based on the constrained particle swarm optimization, Automatica, Vol. 44, Issue 4, Apr. 2008, p. 1104 – 1110.
21. Mukherjee V., Ghoshal S. P., Intelligent particle swarm optimized fuzzy PID controller for AVR system, Electric Power Systems Research, V. 77, Issue 12, Oct. 2007, p. 1689 – 1698.