Sensitivity of Design Parameters on the Constant-Force Behavior of Compliant Slider Mechanisms
Ikechukwu Celestine UGWUOKE, Matthew Sunday ABOLARIN, and
Obiajulu Vincent OGWUAGWU
Department of Mechanical Engineering, Federal University of Technology, Minna, Niger State, Nigeria.
E-mails:ugwuokeikechukwu@yahoo.com, abolarinmatthew@yahoo.com
Abstract
This paper highlights the significance of sensitivity analysis as a basis for the dynamic synthesis of compliant mechanisms. Based on the results obtained from the sensitivity analysis, four models were developed and simulation results show that for model 1, at a frequency of 44.5 rad/s, the mechanism yielded a median force of 135.4N with a force variance of±0.3N, for model 2, at a frequency of 41.5 rad/s, it yielded a median force of 91.9N with a force variance of ±0.4N, for model 3, at a frequency of 35 rad/s, the compliant slider mechanism yielded a median force of 92.7N with a force variance of ±1.8N and for model 4, at a frequency of 44 rad/s, it yielded a median force of 73.4N with a force variance of ±0.3N. The results obtained shows the effectiveness of this method in improving the dynamic behavior of compliant mechanisms and also shows that, depending on what attributes are most desirable, the compliant slider mechanism parameters can be optimized to achieve the desired results.
Keywords
Sensitivity analysis, Design parameters, Compliant slider mechanism, Simulation.
Introduction
The field of compliant mechanisms is relatively new, and many design research issues are still unanswered. The potential of compliant mechanisms to produce no-assembly designs gives rise to many applications. They are particularly suited for applications with small ranges of motions. These monolithic devices can potentially replace conventional mechanisms in applications where small but intricate motions are generated by a system of links, cams, and gears. Examples of such systems can be found in cameras, VCR’s, and other mechatronic systems. As the research matures in this area, we can expect to identify more and more applications of compliant mechanisms in the near future (Kota et al., 1999). Compliant mechanisms are single-piece flexible structures that deliver the desired motion by undergoing elastic deformation as opposed to rigid body motions of conventional mechanisms. Deployment of compliant mechanisms can significantly benefit the field of adaptive/smart structures, for they provide a simple and cost-effective means to accomplish controlled motion and force generation without the burden of an excessive number of actuators, as is currently practiced (Kota et al., 1999). At the micro and nano scales, compliant mechanisms dominate conventional rigid body mechanisms because of their ease of fabrication, scalability, superior dynamic response and wear resistance (Mankame and Ananthasuresh, 2002). The past couple of decades has witnessed extensive research in studying the kinematic and kinetostatic behavior of compliant mechanisms (Midha, 1993; Salamon and Midha, 1992; Her and Midha, 1987; Howell and Midha, 1994; Murphy et al., 1994) as well as in the development of techniques for their systematic synthesis (Ananthasuresh and Kota, 1995; Frecker et al., 1997; Sigmund, 1997; Saxena and Ananthasuresh, 2000). This paper highlights the significance of sensitivity analysis as a basis for the dynamic synthesis of compliant mechanisms
Sensitivity Analysis
Sensitivity analysis is an effective way to predict the influence of various physical parameters on the performance of a compliant mechanism. It can be used very effectively to guide the redesign efforts in tuning the design parameters for desired dynamic performance. Minimizing the sensitivity of the response to system parameters can make the design robust and insensitive to manufacturing errors or overload. Sensitivity analysis for optimal design problems where the state is governed by a variation inequality is a topic of continuing research because the problem is inherently non-differentiable and only directional sensitivities can be expected (Mankame and Ananthasuresh, 2002). A method of sensitivity analysis based on the direct differentiation of the equilibrium equation with respect to design variables is presented.
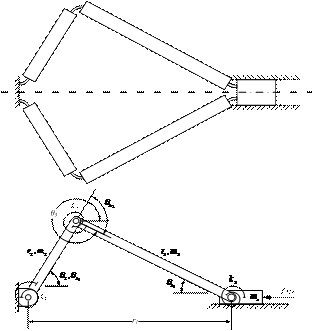
Figure 1. The compliant slider mechanism and its pseudo-rigid-body model
The dynamic equilibrium equation of motion for the compliant slider mechanism can be derived using Lagrange’s equation of motion given as
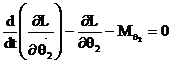
where ![]() = Generalized
position coordinates
= Generalized
position coordinates
The Lagrangian![]() for a conservative system is formed by
taking the difference of the scalar quantities of kinetic energy T and
potential energy V of the system.
for a conservative system is formed by
taking the difference of the scalar quantities of kinetic energy T and
potential energy V of the system.
![]()
The sensitivity formulae with respect to certain physical parameter S of the compliant slider mechanism is given as
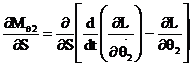
The design parameters considered are the mass ![]() of the rigid links and the
stiffness
of the rigid links and the
stiffness ![]() of
the flexural joints of mechanism. The sensitivity of the constant-force behavior
of the compliant slider mechanism to design parameters is derived as follows
of
the flexural joints of mechanism. The sensitivity of the constant-force behavior
of the compliant slider mechanism to design parameters is derived as follows
![]()
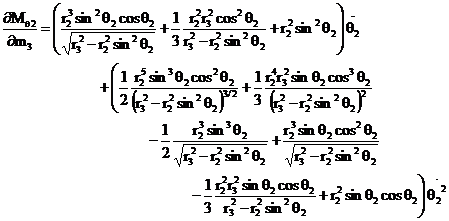
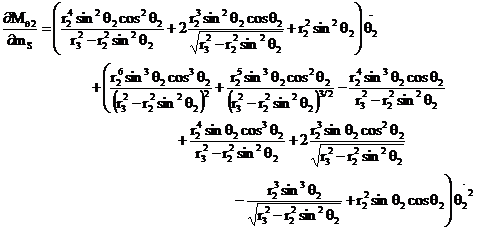
![]()
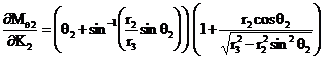
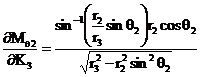
Torque ![]() is
transformed to mechanism’s output force F using the power relationship which is
expressed as follows:
is
transformed to mechanism’s output force F using the power relationship which is
expressed as follows:
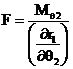
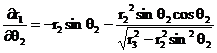
Results and Discussion
Sensitivities of the mass of the rigid links of the mechanism and also the stiffness of the flexural joints on the constant-force behavior of the compliant slider mechanism were carried out and the results presented in Figures 2 through 7. Table 1 shows the mechanism parameters used for the simulation. The sensitivity of the mean force to the mass of the rigid links and also to the stiffness of the flexural joints of the mechanism is shown in Figures 2 and 3. Results show that the most effective means to reduce the mean force magnitude of the compliant slider mechanism would be to
1. Reduce the mass of link 2, and/or 3
2. Reduce the stiffness of flexural joint ![]()
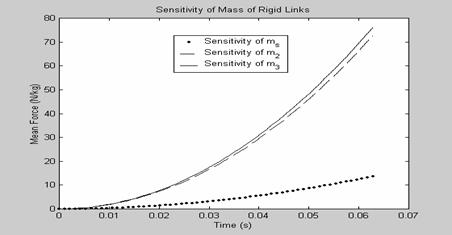
Figure 2. Sensitivity of mean force to the mass of rigid links of mechanism
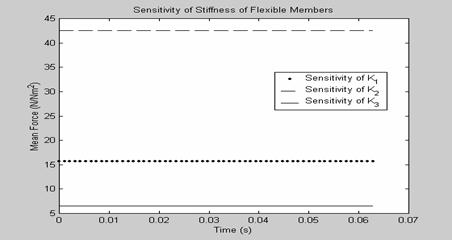
Figure 3. Sensitivity of mean force to the stiffness of flexural joints of mechanism
As shown in Figure 4, the sensitivity of the median force to the mass of the rigid links of the mechanism, links 2 and 3 is negative while that with respect to the slider mass is positive. Sensitivity of the median force as shown in Figure 5, to the stiffness of the flexural joints of the mechanism, is positive. Results, as shown in Figures 4 and 5, shows that the most effective means to reduce the median force magnitude of the compliant slider mechanism would be to
1. Increase the mass of link 2, and/or 3
2. Reduce the mass of slider
3.
Reduce the stiffness of flexural joint ![]()
Table 1:.Mechanism Parameters
|
Mechanism Parameters |
Model 1 Parameter Values |
Model 2 Parameter Values |
Model 3 Parameter Values |
Model 4 Parameter Values |
|
r2 |
90 mm |
90 mm |
90 mm |
90 mm |
|
r3 |
120 mm |
120 mm |
120 mm |
120 mm |
|
m2 |
0.026kg |
0.013kg |
0.052kg |
0.013kg |
|
m3 |
0.037 kg |
0.0185 kg |
0.074 kg |
0.0185 kg |
|
ms |
0.087kg |
0.087kg |
0.0435kg |
0.0435kg |
|
K1 |
2.671 Nm |
2.671 Nm |
2.671 Nm |
1.336 Nm |
|
K2 |
2.290 Nm |
1.145 Nm |
1.145 Nm |
1.145 Nm |
|
K3 |
2.003 Nm |
2.003 Nm |
2.003 Nm |
2.003 Nm |
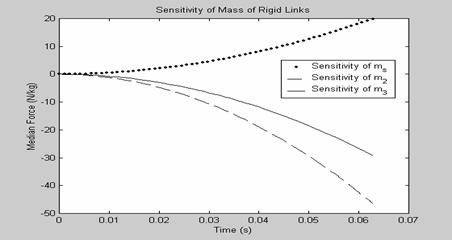
Figure 4. Sensitivity of median force to the mass of rigid links of mechanism
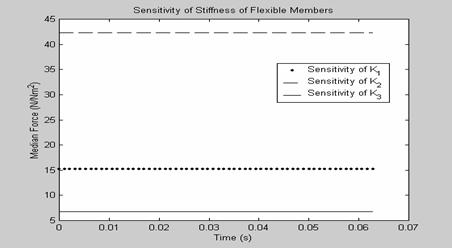
Figure 5. Sensitivity of median force to the stiffness of flexural joints of mechanism
As shown in Figure 6, sensitivity of the peak-to-peak force magnitude to the mass of the rigid links of the mechanism is positive. Figure 7 shows that the Sensitivity of the peak-to-peak force magnitude to the stiffness of the flexural joints of the mechanism is also positive. Based on results, as shown in Figures 6 and 7, the most effective means to reduce the peak-to-peak force magnitude of the compliant slider mechanism would be to
1. Reduce the mass of link 2, and/or 3
2. Reduce the mass of slider
3.
Reduce the stiffness of flexural joint ![]()
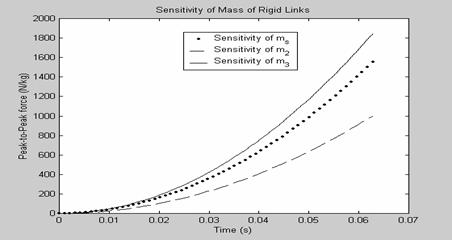
Figure 6. Sensitivity of peak-to-peak force to the mass of rigid links of mechanism
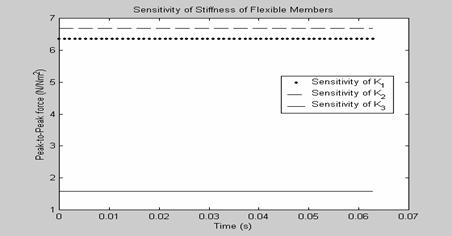
Figure 7. Sensitivity of peak-to-peak force to the stiffness of flexural joints of mechanism
Based on the results obtained from the sensitivity analysis of the compliant slider mechanism, four models were developed; this is shown in table 1. The predicted force for the various models as a function of time and position for a sinusoidal input of 100 rad/s is shown in Figures 8 and 9. In the evaluation of the dynamic models, three useful plots were analyzed, the mean force, the median force and the peak-to-peak force magnitude difference as a function of frequency as shown in Figures 10, 11 and 12. Each frequency assumes a sinusoidal position input with amplitude equal to the full 40% designed mechanism deflection with a slight pre-displacement to give a preload at full expansion.
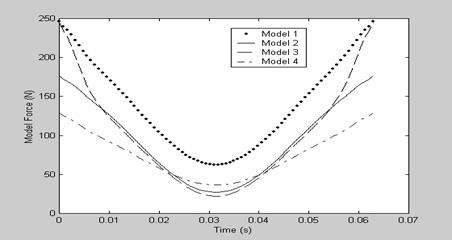
Figure 8.
Predicted force for sinusoidal input![]()
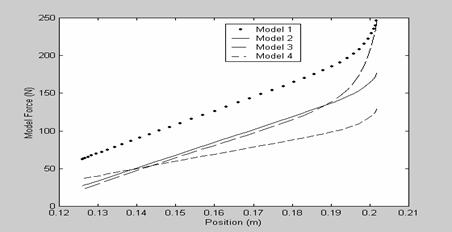
Figure 9. Position force diagram for the various models
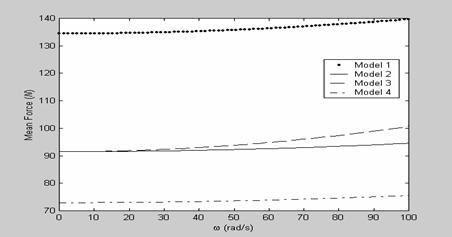
Figure 10. Frequency plots depicting the mean force exhibited by mechanism
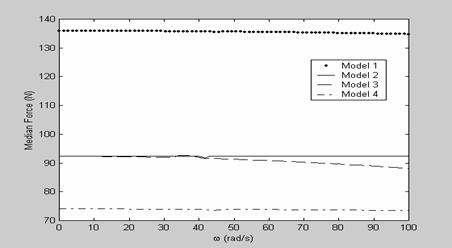
Figure 11. Frequency plots depicting the median force exhibited by mechanism
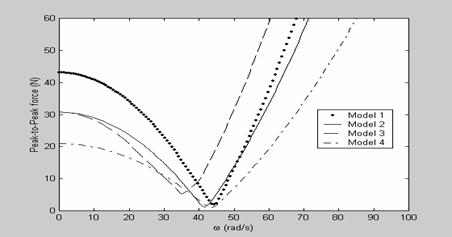
Figure 12. Frequency plots depicting the peak-to-peak magnitude difference
Results for a single frequency with a very low peak-to-peak force for the various model have been tabulated, this is shown in table 2. The results show that for model 1, at a frequency of 44.5 rad/s, the compliant slider mechanism yielded a median force of 135.42N with a force variance of ±0.34N, demonstrated clearly in Figure 13, for model 2, at a frequency of 41.5 rad/s, it yielded a median force of 91.88N with a force variance of ±0.37N as shown in Figure 14, for model 3, at a frequency of 35.0 rad/s, the mechanism yielded a median force of 92.65N with a force variance of ±1.78N, shown clearly in Figure 15 and for model 4, at a frequency of 44.0 rad/s, it yielded a median force of 73.42N with a force variance of ±0.33N, this is shown clearly in Figure 16. The results obtained show the effectiveness of this method in improving the dynamic behavior of compliant mechanisms.
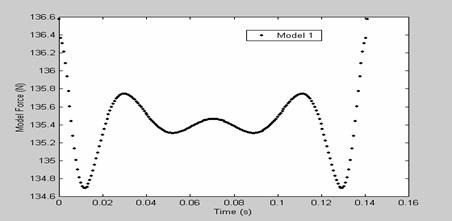
Figure 13. Force predicted by model 1 for sinusoidal input of ω = 44.5 rad/s
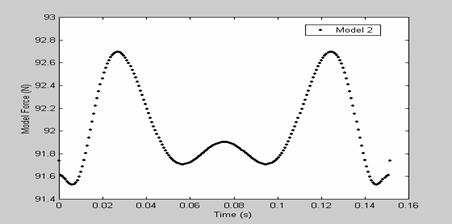
Figure 14. Force predicted by model 2 for sinusoidal input of ω = 41.5 rad/s
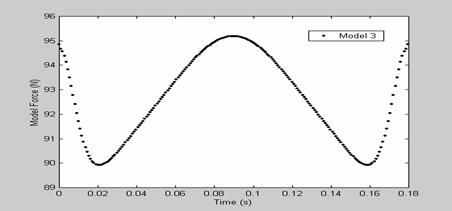
Figure 15. Force predicted by model 3 for sinusoidal input of ω = 35.0 rad/s
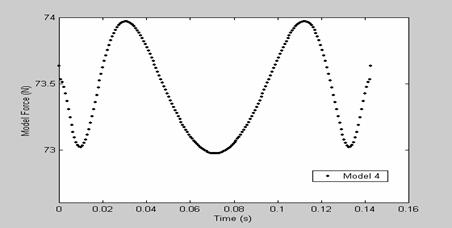
Figure 16. Force predicted by model 4 for sinusoidal input of ω = 44.0 rad/s
Table 5.2: Simulation result for the various models
|
Model |
Frequency (rad/s) |
Force Variance (N) |
Mean Force (N) |
Median Force (N) |
PCF (%) |
|
1 |
44.5 |
± 0.3449 |
135.4214 |
135.4156 |
98.6216 |
|
2 |
41.5 |
± 0.3698 |
92.0205 |
91.8799 |
98.7399 |
|
3 |
35.0 |
± 1.7832 |
92.5997 |
92.6505 |
94.4632 |
|
4 |
44.0 |
± 0.3391 |
73.4425 |
73.4193 |
98.6493 |
Depending on what attributes are most desirable, the compliant slider mechanism parameters can be optimized to achieve the desired results. A wide frequency band with moderately low peak-to-peak force, a single frequency with very low peak-to-peak force or some other similar effects can be achieved simply by varying mechanism parameters.
Conclusion
The field of compliant mechanisms is relatively new, and many design research issues are still unanswered. As the research matures in this area, we can expect to identify more and more applications of compliant mechanisms in the near future. A method of design analysis is presented based on sensitivity analysis carried out on the compliant slider mechanism. Sensitivity analysis is an effective way to predict the influence of various design parameters on the performance of a compliant mechanism. It can be used very effectively to guide the redesign efforts in tuning the design parameters for desired dynamic performance. Based on the result of sensitivity analysis, four models were developed and simulation results show the effectiveness of this method in improving the dynamic behaviors of compliant mechanisms in this case, compliant slider mechanisms.
References
1. Kota, S.; Hetrick, J.; Li, Z.; and Saggere, L., Tailoring Unconventional Actuators Using Compliant Transmissions: Design Methods and Applications, IEEE/ASME Transactions on mechatronics, Vol. 4, No. 4, pp 396-408, 1999.
2. Mankame, N.D. and Ananthasuresh, G.K., Contact Aided Compliant Mechanism: Concept and Preliminaries, Proceedings of DETC 2002 ASME Design Engineering Technical Conferences, Sept. 29, 2002, Montreal, Quebec, Canada. 2002
3. Midha, A. Modern kinematics-The developments in the last forty years, Chapter 9: Elastic mechanisms, (ed. A. G. Erdman). John Wiley and Sons Inc., NY, 1993
4. Salamon, B.A. and Midha, A., An introduction to mechanical advantage in compliant mechanisms. Advances in design automation, Proc. of the ASME 1992 Design automation conference, DE-Vol44 (2):47–51, 1992.
5. Her, I. and Midha, A., A compliance number concept for compliant mechanisms and type synthesis. Trans. of the ASME, Journal of mechanisms, transmissions and automation in design, 109:348–355, 1987.
6. Howell, L.L.; and Midha, A., The development of force-deflection relationships for compliant mechanisms. Machine elements and Machine dynamics, Proc. of the ASME
1994 Design Technical Conferences, Minneapolis, MN, DE-Vol71:501–508, 1994.
7. Murphy, M.D.; Midha, A.; and Howell, L.L., Methodology for the design of compliant mechanisms employing type synthesis techniques with example. Mechanism synthesis and analysis, Proc. of the ASME 1994 Design Technical Conferences, Minneapolis, MN, DE-Vol70:61–66, 1994.
8. Ananthasuresh, G.K. and Kota, S., Designing compliant mechanisms. Mechanical Engineering, Magazine of the ASME, 117(11):93–96, 1995.
9. Frecker, M.; Ananthasuresh, G.K.; Nishiwaki, S.; Kikuchi, N.; and Kota, S., Topological synthesis of compliant mechanisms using multi-criteria optimization. Trans. of the ASME, Journal of Mechanical Design, 119(2):238–245, 1997.
10. Sigmund, O., On the design of compliant mechanisms using topology optimization. Mec. Struct. and Mach., 25(4):493–524, 1997.
11. Saxena, A.; and Ananthasuresh, G.K., on an optimal property of compliant topologies. Structural and Multidisciplinary optimization, 19(1):36–49, 2000.