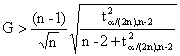Observation vs. Observable: Maximum Likelihood Estimations according to the Assumption of Generalized Gauss and Laplace Distributions

Lorentz JÄNTSCHI^1*, and Sorana D. BOLBOACĂ^1,2

¹ Technical University of Cluj-Napoca, 103-105 Muncii Boulevard, 400641 Cluj-Napoca, Cluj, Romania.

²”Iuliu Haţieganu” University of Medicine and Pharmacy Cluj-Napoca, 13 Emil Isac, 400023 Cluj-Napoca, Cluj, Romania.

E-mail(s): lori@academicdirect.org; sbolboaca@umfcluj.ro.

(^* Corresponding author)

Abstract

Aim: The paper aims to investigate the use of maximum likelihood estimation to infer measurement types with their distribution shape. Material and Methods: A series of twenty-eight sets of observed data (different properties and activities) were studied. The following analyses were applied in order to meet the aim of the research: precision, normality (Chi-square, Kolmogorov-Smirnov, and Anderson-Darling tests), the presence of outliers (Grubbs’ test), estimation of the population parameters (maximum likelihood estimation under Laplace, Gauss, and Gauss-Laplace distribution assumptions), and analysis of kurtosis (departure of sample kurtosis from the Laplace, Gauss, and Gauss-Laplace population kurtosis). Results: The mean of most investigated sets was likely to be Gauss-Laplace while the standard deviation of most investigated sets of compound was likely to be Gauss. The MLE analysis allowed making assumptions regarding the type of errors in the investigated sets. Conclusions: The proposed procedure proved to be useful in analyzing the shape of the distribution according to measurement type and generated several assumptions regarding their association.

Keywords

Statistical inference; Accuracy; Observation; Maximum likelihood estimation.

Introduction

Experimental data plays an important role in the validity of quantitative Structure-Activity Relationship (qSAR) models. The precision and accuracy of experimental data influence the uncertainty of a qSAR model. The variability in the descriptors values used in modeling [1], the correct choice of the variables involved, the factors that influence the activity/property [2] also influence the validity of qSAR models. The accuracy refers to how experiments are carried out. The two types of errors (gross errors) that may occur can be eliminated by checking instruments against the standard, repeating measurements, using standard procedures, calibrating devices, etc. These types of errors could be classified as instrumental (always limited by the equipment and protocol used) and human (natural human biases, as for example reading errors). Experimental accuracy could be related to the existence of systemic errors (e.g. differences between laboratories, differences between researchers, etc.) [3]. Consequently, the statistical identification of any types of errors in experimental data is a relevant issue in qSAR analyses due to its impact on the estimation / prediction model.

Maximum likelihood (ML) [4] is a method used to find parameters that maximize the observation probability. The main properties of the maximum likelihood method are as follows [5]: ▪ consistency (the estimated MLE parameter is asymptotically consistent (n→∞)); ▪ normality (the estimated MLE parameter is asymptotically, normally distributed with minimal variance); ▪ invariance (the maximum likelihood solution is invariant when parameters change); ▪ efficiency (if efficient estimators exist for a give problem, the maximum likelihood method will find them). The method may also be used to evaluate the uncertainty of qSAR models [6-9].

The present research aimed to use the maximum likelihood estimation method in order to assess the association between measurement types and the power of error according to error type.

Material and Method

Sets of Compounds

Twenty-eight sets of compounds with a different property / activity were investigated. The measured property or activity was taken from previously reported research. A summary of the investigated sets of compounds expressed as sample size, set abbreviation, activity/property, existence of ties and associated references are presented in Table 1.

Table 1. Investigated sets of compounds

No.	n	Set [ref]	Activity / Property	Ties
1	209	Y209 [10]	Chromatographic retention times	Yes
2	209	RRF [11]	Relative response factor	Yes
3	206	Y206 [12]	Octanol-water partition coefficient (logKow)	Yes
4	205	Y205 [13]	Octanol-water partition coefficient (logKow)	Yes
5	166	C166 [14]	Thermodynamic solubility	Yes
6	143	OrgPest [15,16]	Soil sorption coefficients (KOC)	Yes
7	126	Anthra [17-23]	Toxicity on HepG2 cells (logIC50) ^c	Yes
8	111	MPC [24-27]	Molecular partition coefficient in n-octanol / water system (logP)	Yes
9	105	MDL [28-38]	Brain-blood partition coefficient (logBBP)	Yes
10	88	Diamino [39,40]	Antibacterial inhibitory activity (-logIC50) ^f	Yes
11	87	lnCHF [41]	Concentration high food (ng/g - lnCHF)	Yes
12	69	AAT [42]	Acute aquatic toxicity (-log[LC50]) LC50^a	Yes
13	63	DZGALYL [43]	Resistance index (RI) ^d (-log(RI[taxoid]/RI[paclitaxel]))	No
14	63	IMHH [44]	Brain-blood partition coefficient (logBBP)	Yes
15	57	InHIV [45]	HIV1 inhibition (log(10^6/C50)) C50^b	No
16	58	InACE [46]	ACE inhibition activity (log(1/IC50)) IC50^c	Yes
17	57	Clark [47]	Brain-blood partition coefficient (logBBP)	Yes
18	48	BTA [46]	Bitter tasting activity (log(1/T))	Yes
19	47	MASIS-CAII [48]	Carbonic anhydrase II inhibitory activity (KI, nM))	Yes
20	45	MCY [49,50]	Brain-blood partition coefficient (logBBP)	No
21	43	BKST [51]	Protonation constant (pKa)	No
22	40	CAI [52]	Carbonic anhydrase I inhibitory activity (logIC50, nM)	Yes
23	40	CAII [52]	Carbonic anhydrase II inhibitory activity (logIC50, nM)	Yes
24	40	CAIV [52]	Carbonic anhydrase IV inhibitory activity (logIC50, nM)	Yes
25	39	Nitro [53]	Toxicity (logLD50, LD50^f (mg/kg))	Yes
26	35	MGWTI [54]	Cell growth inhibitory activity (log1/IC50, IC50 ^c)	Yes
27	29	TTKSS-CAII [55]	Carbonic anhydrase II inhibitory activity (logKc)	Yes
28	25	ERBAT [56]	Estrogen receptor binding affinity (logRBA, LBA ^e)	Yes
n = sample size; Ties = existence of more than one compound with the same value of property/activity ^aLC50 = 50% lethal dose concentration ^bC50 = compound concentration required to achieve 50% protection of MT-4 cells against HIV ^cIC50 = compound concentration required for 50% growth inhibition ^dInhibitory effect (IC50) to drug sensitive human breast carcinoma (MCF-7S) and multidrug-resistance human breast carcinoma (MCF-7R) – in vitro ^e Relative binding affinity to the estrogen receptor vis-à-vis E2

Method

Experimental data were analyzed progressively in order to achieve the aim of the research:

§ Precision analysis. A series of statistical parameters were calculated in order to characterize the observed data (minimum, maximum, skewness, kurtosis, standard deviation, coefficient of variance (CV=s/m), variance-to-mean ratio (also knows as index of dispersion, VMR = s²/m). Standard deviation is associated with errors in each individual measurement. The skewness evaluated the asymmetry of the distribution while the kurtosis showed how far away the distribution of data was from the Gaussian shape. The following interpretations for skewness were used [57]: -0.5 < skewness < 0.5: distribution is approximately normal; -1 < skewness < -0.5 or 0.5 < skewness > 1: distribution is moderately skewed; skewness < -1 or skewness > 1: distribution is highly skewed. The data were considered normally distributed if the kurtosis was approximately zero; a kurtosis value higher than 0 indicated a leptokurtic distribution; a kurtosis value below 0 indicated a platikurtic distribution [58].

§ Distribution analysis. Three hypotheses regarding the distribution of observed data were tested (Laplace, Gauss and Gauss-Laplace) using the EasyFit software [59]. The following tests were applied: Chi square [60], Kolmogorov Smirnov [61] and Anderson Darling [62]. The Anderson-Darling test was applied because it gives more importance to the tails compared to the Kolmogorov-Smirnov test. Moreover, Anderson-Darling is sensitive to ties [61]. The outliers seem to bring type II errors to the Kolmogorov-Smirnov test (null hypothesis is accepted even if not true) and type I errors (null hypothesis is rejected even if true) to Anderson-Darling statistics [63].

§ Grubbs analysis. Grubbs test [64] was applied whenever appropriate in order to adjust the obliquity of experimental data (skewness; -0.5 < skewness < 0.5: distribution was considered as approximately symmetric). The characteristics of Grubbs test are as follows:

a) Grubbs’ statistics:

G = [max|Yi - m|]/s

Eq(1)

where I = identification number of compound from the data set (1 ≤ i ≤ n); m = sample mean; s = sample standard deviation.

b) The test is rejected for two-sided hypothesis if:

Eq(2)

where n = sample size,  = critical value of the t-distribution with (n-2) degree of freedom at a significance level of α.

§ Error analysis. Maximum likelihood estimation (MLE) was used as statistical method for fitting the experimental data of the investigated sets in order to estimate a series of parameters of the model. The following formulas were used:

	Eq(3)
	Eq(4)

where X_i = measured property / activity for compound i (1 ≤ i ≤ n); μ = population mean; σ = population standard deviation; p = power of error; Γ - gamma function.

The GL(x;μ,σ,p) probability density function features two particular cases: when p = 1 (fixed) it becomes the Laplace (or error) distribution, and when p = 2 (fixed) it becomes the Gauss (or normal) distribution.

The sample mean of each set of compounds was considered the maximum likelihood estimation of the population mean; the sample variance was considered the maximum likelihood estimator of the population variance. Three cases of hypothetical distributions were investigated in this research: Laplace (p = 1), Gauss (p = 2), and Gauss-Laplace (power of error to be estimated) [13]. For each distribution, the population statistical parameters were calculated (mean and standard deviation; also power of error for Gauss-Laplace).

The association of measurement type with the power of error (p) according to the type of error was also investigated (Laplace (p = 1) as model for relative error and Gauss (p = 2) for absolute error).

§ Kurtosis analysis. The kurtosis of the samples was computed for Laplace (p = 1), Gauss (p = 2) and Gauss-Laplace (p as resulted from MLE). The following kurtosis formula for the investigated distributions was used to analyze the distance between the sample kurtosis and the expected population kurtosis:

Eq(5)

The following two particular cases occurred: Laplace (p = 1) with KurtosisGL(1) = 6 and Gauss (p = 2) with KurtosisGL(2) = 3.

Results and Discussion

Descriptive statistic parameters expressed as mean (m), standard deviation (s), minim (min), maxim (max), skewness (skew), kurtosis (kurt), coefficient of variance (CV) and variance-to-mean ratio (VMR) for the investigated sets of compounds were calculated and are presented in Table 2.

Table 2. Descriptive statistics of investigated property / activity

Set	n	min	max	m	s	skew	kurt	VMR	CV (%)
Y209	209	0.10	1.05	0.60	0.18	-0.13	2.72	0.054	30
RRF	209	0.03	2.04	0.77	0.35	0.56	3.67	0.162	46
Y206	206	4.15	9.60	6.48	0.83	0.25	3.85	0.106	13
Y205	205	4.15	9.14	6.47	0.80	0.05	3.28	0.099	12
C166	166	-6.00	3.35	-0.35	1.81	-0.49	3.20	n.a.	n.a.
OrgPest	143	0.42	5.31	2.52	0.91	0.77	3.68	0.327	36
Anthra	126	3.45	7.70	4.74	0.78	1.60	5.94	0.127	16
Anthra-GO	124	3.45	7.05	4.70	0.69	1.36	5.17	0.103	15
MPC	111	-0.44	4.79	1.90	1.01	-0.03	2.98	0.538	53
MDL	105	-2.00	1.44	-0.09	0.77	-0.47	2.86	n.a.	n.a.
Diamino	88	3.10	6.00	4.84	0.52	-0.81	4.18	0.056	11
Diamino-GO	87	3.51	6.00	4.86	0.49	-0.58	3.56	0.049	10
lnCHF	87	0.26	5.77	3.22	1.19	-0.23	2.69	0.442	37
AAT	69	3.04	6.37	4.25	0.76	0.68	2.93	0.136	18
DZGALYL	63	-0.57	2.28	0.74	0.68	0.34	2.66	n.a.	n.a.
IMHH	63	-2.15	1.04	-0.16	0.79	-0.61	2.70	n.a.	n.a.
InHIV	57	3.07	8.62	6.54	1.50	-0.60	2.36	0.345	23
InACE	58	1.77	5.80	3.05	1.00	1.09	3.62	0.329	33
Clark	57	-2.15	1.04	-0.14	0.79	-0.68	2.89	n.a.	n.a.
BTA	48	1.13	3.60	1.98	0.63	0.84	2.91	0.199	32
MASIS-CAII	47	0.86	2.51	1.75	0.51	-0.25	1.79	0.149	29
MCY	45	-2.00	1.04	0.00	0.71	-0.95	3.76	n.a.	n.a.
ERBAT	25	-2.00	2.22	0.38	1.38	-0.47	1.98	n.a.	n.a.
CAI	40	0.00	2.66	0.85	0.54	1.45	7.60	0.338	63
CAII	40	-0.70	2.04	0.47	0.52	0.85	6.04	n.a.	n.a.
CAIV	40	-0.30	2.51	0.74	0.54	0.98	6.49	n.a.	n.a.
logCAII-GO	38	-0.70	0.95	0.39	0.38	-0.95	3.55	n.a.	n.a.
logCAIV-GO	38	-0.30	1.45	0.66	0.39	-0.93	3.78	n.a.	n.a.
Nitro	39	3.38	8.77	6.50	1.37	-0.53	3.07	0.291	21
MGWTI	35	-2.00	1.74	-0.69	1.25	0.78	2.15	n.a.	n.a.
logCAI-GO	34	0.30	1.28	0.85	0.25	-0.25	2.78	0.076	30
TTKSS-CAII	29	4.41	9.39	7.44	1.41	-0.48	2.29	0.267	19
BKST	43	5.51	10.53	8.46	1.13	-0.49	3.13	0.151	13
n = sample size; min = minimum; max = maximum; m = sample mean; s = sample standard deviation; skew = skewness; kurt = kurtosis; VMR = Variance-To-Mean Ratio; CV = coefficient of variance

Thirteen out of thirty-three sets of compounds had negative values. The dispersion index and the variance coefficient could not be analyzed for these sets due to these negative values.

The analysis of the skewness revealed that 11 sets of compounds had a moderately skewed distribution (probability to be observed is between 1% and 5%), in 7 sets the distribution was highly skewed (less than 1% probability to be observed) and in 15 sets the distribution was approximately symmetric (no rejection of the symmetry at 5% risk being in error). The highly skewed sets comprised Soil sorption coefficients (OrgPest), Relative response factor (RRF), and some sets which referred to the concentration of compounds required for 50% growth inhibition (Anthra, CAI, InACE and Diamino, the Anthra set remained highly skewed following Grubbs test). According to this parameter, 15 sets of compounds were expected to have approximately symmetric distribution. The analysis of kurtosis revealed that 18 sets of compounds were leptokurtic and 15 platykurtic. According kurtosis values, the toxicity on HepG2 cells (Anthra) and Carbonic anhydrase inhibitory activity CAI, CAII and CAIV sets were expected to have the Laplace distribution (kurtosis > 5).

The analysis of variance-to-mean ratio of the investigated sets of compounds concluded that the data were under-dispersed (0 < VMR < 1) without exception. The analysis of the results obtained by the variation coefficients (as a measure of relative variation) showed a great relative variation (CV ≥ 20) of the experimental data in 17 sets and a small variation (10 ≤ CV < 20) in 9 sets. MPC and CAI presented greatest data variation according to the variation coefficients (see Table 2). The removal of the outlier whenever identified by Grubbs test did not shift the set of compounds between variation classes (see Table 2).

The analysis of the results obtained following the investigation of the null hypothesis “the observed data followed the Laplace distribution” revealed the following (see Table 3):

§ All three applied tests rejected the null hypothesis at a significance level of 5% for 10 sets: RRF, OrgPest, Anthra, Anthra-GO, AAT, InHIV, InACE, BTA, CAII, and CAIV.

§ With two exceptions (AAT and IMHH sets), the Anderson-Darling test rejected the null hypothesis for the same sets of compounds as the Chi-square test: Y209, RRF, Y206, Y205, OrgPest, Anthra, Anthra-GO, MDL, InHIV, InACE, and BTA.

§ With few exceptions, the null hypothesis of Laplace distribution was rejected at different significance levels. The exceptions were: DZGALYL, Clark, MCY, BKST, CAI, Nitro, logCAI-GO, ERBAT.

The Chi-square test rejected the null hypothesis of normality at a significance level of 5% in 5 (RRF, Anthra, Anthra-GO, InACE, and BTA) out of 28 cases (see Table 3). The normality has also been rejected by the Kolmogorov-Smirnov and Anderson-Darling tests for the Anthra and Anthra-GO sets. These two sets of compounds were the ones in which all three normality tests agreed at a 5% significance level. Thus, it can be concluded that the toxicity on HepG2 cells did not respect the normal distribution. Note that the adjustment of the obliquity of experimental data (Grubbs test) from the Anthra set did not lead to a normal distributed data-set. This observation was also true for different significance levels for logCAII-GO and logCAIV-GO, which led to the conclusion that there were errors in the experimental data (unreliable data).

Table 3. Results of Laplace distribution testing: Chi square (CS), Kolmogorov Smirnov (KS) and Anderson Darling (AD) tests

Set	Chi-square					Kolmogorov-Smirnov				Anderson-Darling
	Stat.	df	p	Reject5%	Rejectα%	Stat.	p	Reject5%	Rejectα%	Stat.	Reject5%	Rejectα%
Y209	19.49	7	0.0068	Yes	≥0.01	0.08769	0.0756	No	≥0.1	2.7752	Yes	≥0.05
RRF	28.99	7	1.44∙10^-4	Yes	≥0.01	0.1121	0.0096	Yes	≥0.02	3.2920	Yes	≥0.02
Y206	21.97	7	0.0026	Yes	≥0.01	0.0844	0.1000	No	0.2	2.7284	Yes	≥0.05
Y205	25.19	7	7.03∙10^-4	Yes	≥0.01	0.0920	0.0583	No	≥0.1	3.1799	Yes	≥0.05
C166	11.13	7	0.1331	No	0.2	0.0996	0.0692	No	≥0.1	2.0107	No	≥0.1
OrgPest	24.76	7	8.36∙10^-4	Yes	≥0.01	0.1299	0.0145	Yes	≥0.02	2.566	Yes	≥0.05
Anthra	35.32	6	3.74∙10^-6	Yes	≥0.01	0.1784	5.56E-4	Yes	≥0.01	5.0544	Yes	≥0.01
Anthra-GO	35.32	6	3.74∙10^-6	Yes	≥0.01	0.1610	0.0028	Yes	≥0.01	3.8716	Yes	≥0.01
MPC	10.57	6	0.1026	No	0.2	0.1002	0.2011	No	n.a.	1.5632	No	0.2
MDL	19.49	7	0.0068	Yes	≥0.01	0.0877	.0756	No	≥0.10	2.7752	Yes	≥0.05
Diamino	7.61	6	0.2682	No	n.a.	0.1595	0.0202	Yes	≥0.05	2.040	No	≥0.10
Diamino-GO	9.52	6	0.1460	No	0.2	0.1518	0.0324	Yes	≥0.05	1.8791	No	0.2
lnCHF	9.17	6	0.1645	No	0.2	0.1086	0.2388	No	n.a.	1.5085	No	0.2
AAT	10.69	4	0.0303	Yes	≥0.05	0.1711	0.0309	Yes	≥0.05	2.0787	No	≥0.10
DZGALYL	3.83	5	0.5738	No	n.a.	0.1139	0.3598	No	n.a.	0.9349	No	n.a.
IMHH	11.28	4	0.0236	Yes	≥0.05	0.1316	0.2063	No	n.a.	1.8420	No	0.2
InHIV	13.09	4	0.0108	Yes	≥0.02	0.1870	0.0322	Yes	≥0.05	2.8312	Yes	≥0.05
InACE	14.26	5	0.0140	Yes	≥0.02	0.2011	0.0157	Yes	≥0.02	2.6301	Yes	≥0.05
Clark	7.79	4	0.0996	No	≥0.10	0.1306	0.2614	No	n.a.	1.5585	No	0.2
BTA	12.64	3	0.0055	Yes	≥0.01	0.2518	0.0036	Yes	≥0.01	2.6130	Yes	≥0.05
MASIS-CAII	8.46	4	0.0761	No	≥0.10	0.14928	0.2224	No	n.a.	2.0537	No	≥0.10
MCY	1.39	4	0.8458	No	n.a.	0.14979	0.2398	No	n.a.	1.1642	No	n.a.
BKST	4.01	4	0.4050	No	n.a.	0.1100	0.6351	No	n.a.	0.6320	No	n.a.
CAI	2.77	4	0.5967	No	n.a.	0.1110	0.6667	No	n.a.	0.6642	No	n.a.
CAII	15.34	3	0.0016	Yes	≥0.01	0.221	0.0658	No	≥0.10	2.6033	Yes	≥0.05
CAIV	15.34	3	0.0016	Yes	≥0.01	0.2021	0.0658	No	≥0.10	2.6033	Yes	≥0.05
Nitro	3.26	3	0.3527	No	n.a.	0.1573	0.2611	No	n.a.	0.9967	No	n.a.
logCAII-GO	6.67	3	0.0833	No	≥0.10	0.2667	0.0071	Yes	≥0.01	1.9159	No	0.2
logCAIV-GO	7.28	4	0.1216	No	0.2	0.2288	0.0313	Yes	≥0.05	1.515	No	0.2
MGWTI	6.07	3	0.1085	No	0.2	0.2556	0.0167	Yes	≥0.02	2.8245	Yes	≥0.05
logCAI-GO	0.43	4	0.9796	No	n.a.	0.1322	0.5477	No	n.a.	0.5747	No	n.a.
TTKSS-CAII	5.47	3	0.1402	No	0.2	0.1698	0.3344	No	n.a.	1.1505	No	n.a.
ERBAT	1.45	2	0.4831	No	n.a.	0.1519	0.5601	No	n.a.	1.1865	No	n.a.
Stat. = value of the statistics; df = degree of freedom; Reject5% = reject the hypothesis at a significance level of 5%; Rejectα% = the significance level at which the hypothesis is rejected, whenever appropriate; p = p-value; n.a. = not applicable

The hypothesis of normality was rejected at different significance levels by the Chi-square test in 14 cases (α = 0.2: Y206, MPC, AAT, InHIV, MASIS-CAII, CAI, logCAII-GO; α ≥ 0.10: CAII; α ≥ 0.01: BTA, Anthra, Anthra-GO; α ≥ 0.01: RRF; α ≥ 0.05: IMHH, Clark). An agreement between the applied normality tests (different significance levels, see Table 4) was observed for the RRF and BTA sets.

The Kolmogorov-Smirnov test rejected the hypothesis of normality at a 5% significance level in four sets: Anthra, Anthra-GO, MCY and logCAII-GO. Note that the hypothesis of normality was only rejected by the Kolmogorov-Smirnov test for the MCY and logCAII-GO sets.

Anderson-Darling, a less conservative normality test, rejected the hypothesis of normality at a 5% significance level in only 2 cases (Anthra and Anthra-GO sets, see Table 4).

The normality analysis showed that the following sets of compounds were not expected to present  the shortest distance between the population (modelled through MLE) and the sample mean and between the population and sample standard deviation according to the Gauss assumption (p = 2): RRF, Anthra, Anthra-GO, Clark, BTA, MCY, and logCAII-GO.

The analysis of the results obtained following the investigation of the null hypothesis “the observed data followed the Gauss-Laplace distribution” revealed the following (see Table 5):

§ The null hypothesis of Gauss-Laplace distribution was rejected at a 5% significance level in all three tests for the Anthra and Anthra-GO sets.

§       The null hypothesis of Gauss-Laplace distribution was rejected at different significance levels in all three tests for the RRF and logCAII-GO sets.

As far as the distribution analysis is concerned, the following conclusions could be drawn:

§ The null hypotheses of investigated distributions were rejected by at least two out of three applied tests at different significance levels in the following sets: RRF, Anthra, Anthra-GO, Clark, BTA, CAII, logCAIV-GO, and MGWTI.

§ The following data sets proved to be normally distributed: Y209, Y205, C166, MDL, Diamino-GO, lnCHF, DZGALYL, BKST, CAIV, Nitro, logCAI-GO, TTKSS-CAII, and ERBAT. A MLR analysis should be applied to these sets.

§ The Gauss-Laplace distribution proved to be less frequently rejected than the Gauss or Laplace distributions.

Table 4. Results of Gauss distribution testing: Chi square (CS), Kolmogorov Smirnov (KS) and Anderson Darling (AD) tests

Set	Chi-square					Kolmogorov-Smirnov				Anderson-Darling
	Stat.	df	p	Reject5%	Rejectα%	Stat.	p	Reject5%	Rejectα%	Stat.	Reject5%	Rejectα%
Y209	1.92	7	0.9641	No	n.a.	0.0314	0.9823	No	n.a.	0.1423	No	n.a.
RRF	17.15	7	0.0165	Yes	≥ 0.02	0.0857	0.0873	No	≥ 0.10	1.545	No	0.20
Y206	11.00	7	0.1386	No	0.20	0.0335	0.9691	No	n.a.	0.4443	No	n.a.
Y205	8.64	7	0.2793	No	n.a.	0.0358	0.9469	No	n.a.	0.3788	No	n.a.
C166	2.99	7	0.8862	No	n.a.	0.0551	0.6743	No	n.a.	0.5654	No	n.a.
OrgPest	8.06	7	0.3273	No	n.a.	0.0849	0.2400	No	n.a.	1.7042	No	0.20
Anthra	24.80	5	1.52·10^-4	Yes	≥ 0.01	0.1755	7.24·10^-4	Yes	≥ 0.01	5.6393	Yes	≥ 0.01
Anthra-GO	20.16	6	0.0026	Yes	≥ 0.01	0.1500	0.0067	Yes	≥ 0.01	4.3883	Yes	≥ 0.01
MPC	8.70	6	0.1914	No	0.20	0.0493	0.9378	No	n.a.	0.2463	No	n.a.
MDL	6.76	6	0.3438	No	n.a.	0.1033	0.1987	No	n.a.	1.0269	No	n.a.
Diamino	8.54	6	0.2008	No	n.a.	0.1121	0.2029	No	n.a.	1.4863	No	0.20
Diamino-GO	7.31	6	0.2936	No	n.a.	0.1079	0.2447	No	n.a.	1.2040	No	n.a.
lnCHF	2.17	6	0.9032	No	n.a.	0.0599	0.8954	No	n.a.	0.3052	No	n.a.
AAT	8.05	5	0.1535	No	0.20	0.1093	0.3557	No	n.a.	0.9161	No	n.a.
DZGALYL	4.37	5	0.4978	No	n.a.	0.0733	0.8626	No	n.a.	0.3885	No	n.a.
IMHH	11.39	4	0.0225	No	≥ 0.05	0.1398	0.1551	No	0.20	1.1324	No	n.a.
InHIV	7.59	4	0.1080	No	0.20	0.1472	0.1528	No	0.20	1.2268	No	n.a.
InACE	2.75	5	0.7384	No	n.a.	0.1393	0.1915	No	0.20	1.8257	No	0.20
Clark	10.90	4	0.0277	Yes	≥ 0.05	0.1479	0.1495	No	0.20	1.0176	No	n.a.
BTA	14.46	4	0.0060	Yes	≥ 0.01	0.1977	0.0405	No	≥ 0.05	1.4480	No	0.20
MASIS-CAII	6.37	4	0.1735	No	0.20	0.1099	0.5831	No	n.a.	0.9572	No	n.a.
MCY	5.93	4	0.2048	No	n.a.	0.2003	0.0466	Yes	≥ 0.05	1.5082	No	0.20
BKST	0.48	2	0.7855	No	n.a.	0.1293	0.7505	No	n.a.	0.6314	No	n.a.
CAI	5.55	5	0.1352	No	0.20	0.1643	0.2061	No	n.a.	1.7636	No	0.20
CAII	6.67	3	0.0833	No	≥ 0.10	0.1582	0.2427	No	n.a.	1.4951	No	0.20
CAIV	5.48	4	0.2413	No	n.a.	0.1512	0.2898	No	n.a.	1.2785	No	n.a.
logCAII-GO	7.01	4	0.1354	No	0.20	0.2197	0.0433	Yes	≥ 0.01	1.3180	No	n.a.
logCAIV-GO	0.84	3	0.8395	No	n.a.	0.2010	0.0804	No	≥ 0.10	1.4905	No	0.20
Nitro	0.34	3	0.9518	No	n.a.	0.0985	0.8083	No	n.a.	0.5312	No	n.a.
MGWTI	4.11	3	0.2498	No	n.a.	0.1953	0.1206	No	0.20	1.9225	No	0.20
logCAI-GO	0.43	4	0.9796	No	n.a.	0.1051	0.8093	No	n.a.	0.2895	No	n.a.
TTKSS-CAII	0.98	2	0.6125	No	n.a.	0.1159	0.7891	No	n.a.	0.4444	No	n.a.
ERBAT	2.46	5	0.7828	No	n.a.	0.1217	0.5086	No	n.a.	0.3568	No	n.a.
Stat. = value of the statistics; df = degree of freedom; Reject5% = reject the hypothesis at a significance level of 5%; Rejectα% = the significance level at which the hypothesis is rejected, whenever appropriate; p = p-value; n.a. = not applicable

The maximum likelihood estimation was applied in order to estimate a series of population parameters. The obtained results expressed as MLE value, population mean and population standard deviation are presented in Table 6. The power of error and expected kurtosis (Ku_GL) were also investigated according to the Gauss-Laplace distribution (see Table 6).

Table 5. Results of Gauss-Laplace distribution testing: Chi square (CS), Kolmogorov Smirnov (KS) and Anderson Darling (AD) tests

Set	Chi-square					Kolmogorov-Smirnov				Anderson-Darling
	Stat.	df	p	Reject5%	Rejectα%	Stat.	p	Reject5%	Rejectα%	Stat.	Reject5%	Rejectα%
Y209	1.37	7	0.9864	No	n.a.	0.0270	0.9971	No	n.a.	0.1246	No	n.a.
RRF	17.94	7	0.0123	Yes	≥0.02	0.0922	0.0537	No	≥0.1	1.5687	No	≥0.2
Y206	11.60	7	0.1144	No	0.2	0.0511	0.6359	No	n.a.	0.7665	No	n.a.
Y205	7.65	7	0.3642	No	n.a.	0.0444	0.7976	No	n.a.	0.4958	No	n.a.
C166	2.98	7	0.8864	No	n.a.	0.0525	0.7286	No	n.a.	0.5541	No	n.a.
OrgPest	7.37	7	0.3913	No	n.a.	0.0874	0.2116	No	n.a.	1.6051	No	0.2
Anthra	35.32	6	3.74∙10^-6	Yes	≥0.01	0.1779	5.87E-4	Yes	≥0.01	5.0393	Yes	≥0.01
Anthra-GO	28.45	6	7.74∙10^-5	Yes	≥0.01	0.1528	0.0054	Yes	≥0.01	3.7083	Yes	≥0.02
MPC	8.83	6	0.1835	No	0.2	0.0499	0.9321	No	n.a.	0.2458	No	n.a.
MDL	1.37	7	0.9864	No	n.a.	0.0230	0.9971	No	n.a.	0.1246	No	n.a.
Diamino	8.42	6	0.2091	No	n.a.	0.1338	0.0778	No	≥0.10	1.4811	No	0.2
Diamino-GO	8.21	6	0.2228	No	n.a.	0.1178	0.1652	No	0.2	1.1734	No	n.a.
lnCHF	2.08	6	0.9124	No	n.a.	0.0509	0.9695	No	n.a.	0.2982	No	n.a.
AAT	8.05	5	0.1534	No	0.2	0.1071	0.3804	No	n.a.	0.9035	No	n.a.
DZGALYL	6.97	5	0.2231	No	n.a.	0.0816	0.7652	No	n.a.	0.425	No	n.a.
IMHH	11.86	4	0.0184	Yes	≥0.02	0.1416	0.1451	No	0.2	1.1271	No	n.a.
InHIV	4.71	4	0.3179	No	n.a.	0.1368	0.2157	No	n.a.	1.0520	No	n.a.
InACE	3.13	5	0.6798	No	n.a.	0.1572	0.1021	No	0.2	1.8734	No	0.2
Clark	11.37	4	0.0227	Yes	≥0.05	0.1498	0.1398	No	0.2	1.0195	No	n.a.
BTA	14.46	4	0.0060	Yes	≥0.01	0.1953	0.0444	Yes	≥0.05	1.4305	No	0.2
MASIS-CAII	4.52	4	0.3406	No	n.a.	0.0838	0.8690	No	n.a.	0.5835	No	n.a.
MCY	4.52	4	0.3407	No	n.a.	0.1845	0.0819	No	≥0.10	1.300	No	n.a.
ERBAT	1.28	5	0.9373	No	n.a.	0.1194	0.5325	No	n.a.	0.3477	No	n.a.
CAI	2.77	4	0.5967	No	n.a.	0.1110	0.6667	No	n.a.	0.6642	No	n.a.
CAII	2.24	5	0.8149	No	n.a.	0.1536	0.2731	No	n.a.	0.7541	No	n.a.
CAIV	3.81	4	0.4319	No	n.a.	0.1284	0.4850	No	n.a.	1.0265	No	n.a.
Nitro	0.59	3	0.8989	No	n.a.	0.1010	0.7845	No	n.a.	0.5278	No	n.a.
logCAII-GO	6.91	4	0.1406	No	0.2	0.2303	0.0296	Yes	≥0.05	1.3749	No	0.2
logCAIV-GO	8.75	4	0.0676	No	≥0.10	0.2090	0.0620	No	≥0.10	1.3723	No	n.a.
MGWTI	3.86	3	0.2771	No	n.a.	0.1739	0.2140	No	n.a.	1.8354	No	0.2
logCAI-GO	0.42	3	0.9371	No	n.a.	0.1130	0.7361	No	n.a.	0.3097	No	n.a.
TTKSS-CAII	0.12	3	0.9887	No	n.a.	0.0890	0.9601	No	n.a.	0.3719	No	n.a.
BKST	0.56	2	0.7561	No	n.a.	0.1319	0.7290	No	n.a.	0.6084	No	n.a.
Stat. = value of the statistics; df = degree of freedom; Reject5% = reject the hypothesis at a significance level of 5%; Rejectα% = the significance level at which the hypothesis is rejected, whenever appropriate; p = p-value; n.a. = not applicable

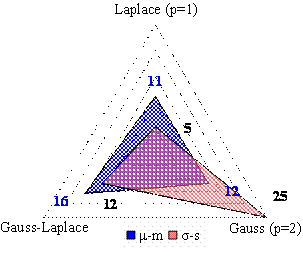
The analysis of the distance between the sample and the population (expected) mean and between the sample and the population standard deviation revealed the following (see Table 6, Figure 1):

§ The mean of most investigated sets was likely to be Gauss-Laplace.

§ The standard deviation of most investigated sets of compound was likely to be Gauss.

Table 6. Results of MLE analysis

Set	G.O.	Laplace (p=1)			Gauss (p=2)			Gauss-Laplace
		MLE	μ	σ	MLE	μ	σ	MLE	μ	σ	p	KuGL
Y209	No	71.55	0.606	0.205	89.27	0.599	0.180	89.85	0.598	0.180	2.331	2.732
RRF	No	-116.37	0.722	0.383	-112.97	0.769	0.352	-111.19	0.746	0.353	1.552	3.648
Y206	Yes	-378.84	6.514	0.931	-365.87	6.481	0.829	-365.32	6.479	0.828	1.791	3.245
Y205	No	-371.62	6.511	0.914	-354.21	6.465	0.801	-354.21	6.465	0.801	2.010	2.990
C166	No	-489.39	-0.261	2.008	-480.78	-0.348	1.802	-480.65	-0.325	1.802	1.846	3.173
OrgPest	No	-272.75	2.400	0.976	-271.92	2.518	0.904	-269.83	2.443	0.906	1.443	3.901
Anthra	Yes	-188.80	4.560	0.735	-211.20	4.740	0.773	-186.89	4.560	0.787	0.784	8.883
Anthra-GO	No	-171.53	4.560	0.679	-187.79	4.695	0.691	-171.04	4.560	0.702	0.879	7.296
MPC	No	-236.94	1.960	1.142	-228.42	1.903	1.007	-228.39	1.900	1.007	2.083	2.922
MDL	No	-176.34	-0.049	0.833	-173.75	-0.094	0.762	-173.47	-0.063	0.764	1.635	3.488
Diamino	Yes	-94.06	4.959	0.546	-96.56	4.841	0.518	-93.87	4.914	0.519	1.302	4.330
Diamino-GO	No	-87.34	4.959	0.521	-87.40	4.86	0.485	-86.35	4.907	0.487	1.458	3.863
lnCHF	No	-208.09	3.190	1.365	-199.63	3.224	1.187	-199.17	3.206	1.187	2.468	2.649
AAT	No	-119.01	4.180	0.860	-113.34	4.254	0.755	-112.98	4.316	0.757	2.595	2.582
DZGALYL	No	-96.32	0.669	0.751	-92.60	0.744	0.670	-92.44	0.768	0.672	2.489	2.637
IMHH	No	-109.06	-0.082	0.864	-106.94	-0.158	0.785	-106.08	-0.306	0.800	3.851	2.213
InHIV	No	-155.61	7.010	1.726	-149.45	6.542	1.489	-146.27	6.337	1.465	3.500	2.282
InACE	No	-120.63	2.788	1.100	-118.13	3.051	0.993	-117.98	2.989	0.993	1.724	3.341
Clark	No	-97.59	-0.074	0.852	-96.18	-0.138	0.779	-96.16	-0.228	0.786	2.775	2.502
BTA	No	-66.72	1.737	0.682	-65.47	1.983	0.622	-64.54	2.149	0.634	4.000	2.188
MASIS-CAII	No	-56.91	1.826	0.602	-49.87	1.749	0.505	-44.75	1.749	0.510	4.000	2.188
MCY	No	-66.51	0.0008	0.732	-69.54	0.0004	0.706	-66.51	0.0006	0.732	1.000	6.000
BKST	No	-96.36	8.500	1.230	-94.88	8.457	1.117	-94.79	8.485	1.117	1.749	3.304
CAI	Yes	-35.90	0.845	0.485	-45.16	0.849	0.529	-35.03	0.845	0.528	0.746	9.749
CAII	Yes	-35.83	0.477	0.484	-43.50	0.474	0.514	-32.76	0.477	0.573	0.588	16.361
CAIV	Yes	-35.87	0.750	0.484	-45.19	0.743	0.529	-33.16	0.701	0.570	0.587	16.430
logCAIV-GO	No	-21.45	0.699	0.385	-25.02	0.657	0.382	-21.11	0.699	0.396	0.885	7.217
logCAII-GO	No	-13.62	0.477	0.338	-14.25	0.442	0.318	-14.09	0.472	0.319	1.620	3.515
Nitro	No	-100.78	6.524	1.560	-96.98	6.496	1.356	-96.95	6.485	1.356	2.150	2.864
MGWTI	No	-84.13	-1.200	1.374	-82.01	-0.692	1.228	-79.96	-0.692	1.246	3.999	2.189
logCAI-GO	No	-4.12	0.845	0.283	-1.661	0.846	0.250	-1.61	0.844	0.250	2.259	2.781
TTKSS-CAII	No	-77.55	7.530	1.660	-72.97	7.444	1.384	-71.16	7.258	1.365	3.774	2.227
ERBAT	No	-65.36	0.531	1.593	-62.19	0.379	1.357	-60.14	0.379	1.385	3.999	2.189
G.O. = Grubbs outliers at significance level of 5%; MLE = Maximum Likelihood Estimation; μ = population mean; σ = population standard error; KuGL = expected kurtosis under Gauss-Laplace assumption

xxxxxxxxxx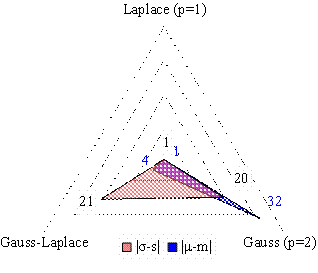

Figure 1. Absolute frequency of the minimum difference between population and sample mean and between population and sample standard deviation (right graph: absolute difference)

§ According to the difference between the population and the sample mean, the following sets of compounds had an activity/property mean that was:

a) Slightly higher than the expected Laplace mean: logCAI-GO, CAI, lnCHF, RRF, AAT, DZGALYL, OrgPest, Anthra-GO, logCAII-GO, Anthra, BTA, InACE, MGWTI.

b) Slightly higher than the expected Gauss mean: logCAII-GO, Diamino-GO, CAII, Anthra, OrgPest, CAI, Diamino, RRF, Y205, AAT, ERBAT, CAIV, MGWTI, Anthra-GO, C166, TTKSS-CAII, Nitro.

c) Slightly higher than the expected Gauss-Laplace mean: InHIV, TTKSS-CAII, logCAII-GO, Anthra, IMHH, Anthra-GO, Clark, OrgPest, InACE, CAIV, RRF, lnCHF, Nitro, CAI, MPC, logCAI-GO, Y206, Y209, Y205, ERBAT.

§ According to the difference between the population and the sample standard deviation, the following sets of compounds proved to present errors in each individual measurement (the sample standard deviation was higher than the population (expected) MLE standard deviation) in terms of:

a) Laplace (p = 1): CAIV, CAI, logCAII-GO, Anthra, CAII, and Anthra-GO.

b) Gauss (p = 2): all investigated sets.

c) Gauss-Laplace: logCAII-GO, TTKSS-CAII, InHIV, Nitro, BKST, InACE, CAI, lnCHF, MPC, C166, logCAI-GO, AAT, DZGALYL, Y206, Y205, MDL, Diamino, Diamino-GO, OrgPest, Y209, MASIS-CAII, Clark, and ERBAT.

Laplace obtained a higher number of agreements in terms of the minimum difference between population and sample mean as well as between population and sample standard deviation (23 sets when the difference was investigated, 33 sets when the absolute difference was investigated). The descending classification of the difference obtained was Laplace – Gauss-Laplace – Gauss and of the absolute difference obtained was Laplace – Gauss – Gauss-Laplace.

The analysis of the power of error (p) calculated by applying the MLE (Gauss-Laplace) revealed the following:

§ Values below 1 were obtained for the following sets: CAIV, CAII, CAI, Anthra, Anthra-GO, logCAIV-GO. In all these sets of compounds the activity referred to the compound concentration required for 50% growth inhibition. IC50 depends on several of factors: concentration of target molecule, concentration of inhibitor, substrate, and other experimental conditions [65, 66].

§ The MCY set was the only set for which an integer number (of 1) was obtained. This set was small, with a sample size of 45 compounds, and did not present any ties. The blood (Cblood) and brain (Cbrain) concentrations, measured in mmol/L with variations in net charge at pH = 7.4 [67] ranged from -2.00 to 1.04.

§ Values higher than 1 and smaller than 2 were obtained for the following sets: Diamino, Diamino-GO, OrgPest, RRF, logCAII-GO, MDL, InACE, BKST, Y206, and C166. Some sets referred to the compound concentrations required for 50% growth inhibition (Diamino, Diamino-GO, logCAII-GO, and InACE), which are subject to different instrumental and human errors. The MDL set comprises a series of compounds collected from different previously reported research. The absence of the same experimental protocol could lead to the obtained results (the blood brain barrier was the observed activity with experimental values ranging from -2.00 to 1.44, very close to the MCY but on a sample of 105 compounds). Other sets from this class referred to the IC50 activity: Diamino, Diamino-GO, logCAII-GO, InACE. The OrgPest set had the soil sorption coefficient of pesticide that measured the chemicals’ propensity to adsorb soil particles. The determination of this coefficient depends on a variety of operational difficulties and experimental artifacts related to the separation of phases, agitation speed, time for equilibration, exposure of new separation phases during agitation, speed of sorption [68]. The response factor was the property investigated for the RRF set. The response factor comprised the area of the target analyte and corresponding internal standard and by their concentrations (subject to instrumental errors and the researcher’s skills). The protonation constant (BKST) and partition coefficient (Y206) belong to the same class of experimental determinations. The thermodynamic solubility of C166 also belongs to this class and it depends on a series of factors (phase, physical properties of solute, temperature, pressure, etc) that could, together with the human factor, influence experimental determinations [69].

§ A value almost equal with 2 was obtained for the octanol-water partition coefficient after removal of the identified outlier [12] (Y205).

§ A value higher than 2 was observed for the following sets: MPC (Molecular partition coefficient in n-octanol / water system), Nitro (Toxicity (logLD50), logCAI-GO (Carbonic anhydrase I inhibitory activity (logIC50), Y209 (Chromatographic retention times), lnCHF (Concentration high food), DZGALYL (Concentration high food), AAT (Acute aquatic toxicity), Clark (Brain-blood partition coefficient), InHIV (HIV1 inhibition (log(106/C50), TTKSS-CAII (Carbonic anhydrase II inhibitory activity), IMHH (Brain-blood partition coefficient), MGWTI (Cell growth inhibitory activity (log(1/IC50)), ERBAT (Estrogen receptor binding affinity), BTA (Bitter tasting activity), and MASIS-CAII (Carbonic anhydrase II inhibitory activity). The value higher than 2 could be explained by the existence of absolute measurement errors. All these sets must be rejected if a MLR (Multiple-Linear regression) analysis on qSAR (quantitative Structure-Activity Relationships) models is conducted.

§ The bitter tasting activity (BTA), a purely subjective activity, proved to have a value of 4. Due to the nature of the observed activity, BTA was expected to have a power of error higher than 2 (Gauss).

The removal of the identified outliers classified the sets of compounds into a higher power of error class as compared with the entire compounds from a data set (an exception from this rule was observed in the logCAIV-GO set). Since this behaviour was only observed in the CAIV set (not in the CAI and CAII sets that belong to the same researchers and are subject to the same errors) it could be concluded that this is related to the carbonic anhydrase IV inhibitory activity.

The kurtosis analysis was performed in terms of distances between the expected population kurtosis (according to the Laplace, Gauss, and Laplace-Gauss assumptions) and the sample kurtosis. The trend evolution showed that the distances according to Gauss and to Laplace followed a similar pattern while the Gauss-Laplace pattern was chaotic (Figure 2).

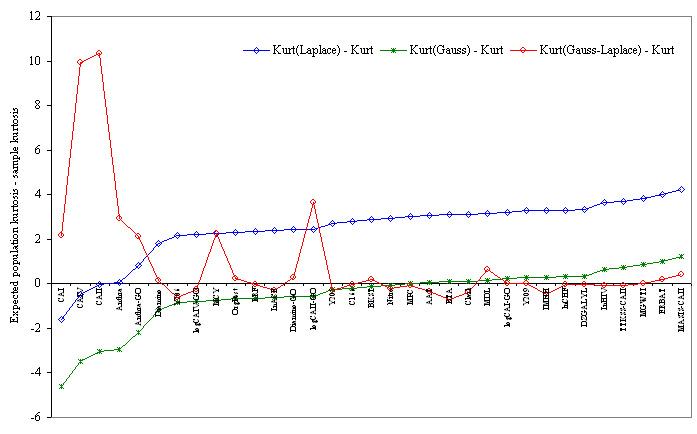
Figure 2. Trends of distance from the expected population kurtosis (Gauss, Laplace and Gauss-Laplace assumptions)

Five sets of investigated compounds proved to be close to the expected Laplace population kurtosis (Anthra, Anthra-GO, CAI, CAII, and CAIV sets). Eleven sets of compounds proved to be closest to the expected Gauss population kurtosis (AAT, BKST, BTA, Clark, IMHH, logCAII-GO, MCY, MDL, MPC, Nitro, and Y205). In most cases, the sample kurtosis proved to be closest to the expected Gauss-Laplace population kurtosis. A significant negative correlation between the minimum distance of the expected Laplace population kurtosis and the sample kurtosis with p (determined by MLE) was obtained by Spearman’s rank correlation coefficient (ρ = -0.621, p = 1.1∙10-4). The sample kurtosis proved to highly correlate with the expected Gauss-Laplace population kurtosis (ρ = 0.908, p = 1.1∙10-6; Cronbach's Alpha coefficient = 0.712) as identified above.

Conclusions

The maximum likelihood approach was applied in order to classify experimental data of active biological compounds. A series of population parameters were estimated according to the Laplace, Gauss and Gauss-Laplace assumptions. The mean of most investigated sets was likely to be Gauss-Laplace while the standard deviation of most investigated sets of compound was likely to be Gauss. The MLE analysis allowed making assumptions regarding the type of errors in the investigated sets. The kurtosis analysis revealed that most investigated sets of compounds were closer to Gauss-Laplace general distribution than expected normal (Gauss) distribution and were not suitable for multiple linear regression analyses.

Acknowledgements

Financial support is gratefully acknowledged to UEFISCSU Romania (ID1051/2007).

References

1. Benfenati E., Clook M., Fryday S., Hart A., QSARs for regulatory purposes: the case for pesticide authorization. In: Benfenati E. (Ed.), Quantitative Structure–Activity Relationship (QSAR) for Pesticide Regulatory Purposes. Elsevier, Amsterdam, Holland, 2007, pp. 1-58.

2. Assmuth T., Lyytimaki J., Hildén M., Lindholm M., Munier B., What do experts and stakeholders think about chemical risks and uncertainties? An Internet Survey, 2007, The Finnish Environment 22. Available at: http://www.environment.fi/download.asp?contentid=71173&lan=en (accessed 10/7/2009)

3. Taylor J. R., An Introduction to Error Analysis. University Science Books, 1982.

4. Fisher R. A., A Mathematical Examination of the Methods of Determining the Accuracy of an Observation by the Mean Error, and by the Mean Square Error, Monthly Notices of the Royal Astronomical Society 1920, 80, p. 758-770.

5. Blobel V. (online), The maximum-likelihood method. Available at: http://www-ttp.particle.uni-karlsruhe.de/GK/Workshop/blobel_maxlik.pdf (accessed 10/07/2009)

6. Liu J., Kern P. S., Gerberick G. F., Santos-Filho O. A., Esposito E. X., Hopfinger A. J., Tseng Y. J., Categorical QSAR models for skin sensitization based on local lymph node assay measures and both ground and excited state 4D-fingerprint descriptors, Journal of Computer-Aided Molecular Design, 2008, 22(6-7), p. 345-366.

7. Pery A., Henegar A., Mombelli E., Maximum-likelihood estimation of predictive uncertainty in probabilistic QSAR modelling, QSAR and Combinatorial Science, 2009, 28(3), p. 338-344.

8. Apostolakis J., Caflisch A., Computational ligand design, Combinatorial Chemistry and High Throughput Screening, 1999, 2(2), p. 91-104.

9. Dimitrov S. D., Mekenyan O. G., Dynamic QSAR: Least squares fits with multiple predictors, Chemometrics and Intelligent Laboratory Systems, 1997, 39(1), p. 1-9.

10. Jäntschi L., Bolboacă S. D., Diudea M. V., Chromatographic Retention Times of Polychlorinated Biphenyls: from Structural Information to Property Characterization, International Journal of Molecular Sciences, 2007, 8(11), p. 1125-1157.

11. Jäntschi L., QSPR on Estimating of Polychlorinated Biphenyls Relative Response Factor using Molecular Descriptors Family, Leonardo Electronic Journal of Practices and Technologies, 2004, 3(5), p. 67-84.

12. Jäntschi L., Bolboacă S. D., Sestraş R. E., Meta-Heuristics on Quantitative Structure-Activity Relationships: A Case Study on Polychlorinated Biphenyls, 2009, DOI: 10.1007/s00894-009-0540-z (Online first).

13. Jäntschi L., Distribution Fitting 1. Parameters Estimation under Assumption of Agreement between Observation and Model, Bulletin of University of Agricultural Sciences and Veterinary Medicine Cluj-Napoca. Horticulture, 2009, 66(2), p. 684-690 (http://arxiv.org/abs/0907.2829).

14. Duchowicz P. R., Talevi A., Bruno-Blanch L. E., Castro E. A., New QSPR study for the prediction of aqueous solubility of drug-like compounds, Bioorganic & Medicinal Chemistry 2008, 16, p. 7944-7955.

15. Duchowicz P. R., González M. P., Helguera A. M., Dias Soeiro Cordeiro M. N., Castro E. A., Application of the replacement method as novel variable selection in QSPR. 2. Soil sorption coefficients, Chemometrics and Intelligent Laboratory Systems 2007, 88, p. 197-203.

16. Gusten S. H., Verhaar H., Hermens J., QSAR modelling of soil sorption. Improvements and systematics of log KOC vs. log KOW correlations, Chemosphere 1995, 31, p. 4489-4514.

17. Huang H. S., Chiu H. F., Chiou J. F., Yeh P. F., Tao C. W., Jeng W. R., Synthesis of Symmetrical 1,5-Bisacyloxy Anthraquinone Derivatives and Their Dual Activity of Cytotoxicity and Lipid Peroxidation, Arch. Pharm. (Weinheim), 2002, 335(10), p. 481-486.

18. Huang H. S., Chiou J. F., Chiu H. F., Chen R. F., Lai Y. L., Synthesis and Cytotoxicity of 9-Alkoxy-1,5-Dichloroanthracene Derivatives in Murine and Human Cultured Tumor Cells, Arch. Pharm. (Weinheim), 2002, 335(1), p. 33-38.

19. Huang H. S., Chiou J. F., Chiu H. F., Hwang J. M., Lin P. Y., Tao C. W., Yeh P. F., Jeng W. R., Synthesis of Symmetrical 1,5-Bisthiosubstituted Anthraquinones for Cytotoxicity in Cultured Tumor Cells and Lipid Peroxidation, Chem Pharm Bull (Tokyo), 2002, 50(11), p. 1491-1494.

20. Huang H. S., Chiu H. F., Lee A. L., Guo C. L., Yuan C. L., Synthesis and structure-activity correlations of the cytotoxic bifunctional 1,4-diamidoanthraquinone derivatives, Bioorganic & Medicinal Chemistry, 2004, 12(23), p. 6163-6170.

21. Huang H. S., Chiu H. F., Yeh P. F., Yuan C. L., Structure-Based Design and Synthesis of Regioisomeric Disubstituted Aminoanthraquinone Derivatives as Potential Anticancer Agents, Helvetica Chimica Acta, 2004, 87(4), p. 999-1006.

22. Huang H. S., Chiu H. F., Lu W. C., Yuan C. L., Synthesis and Antitumor Activity of 1,8-Diaminoanthraquinone Derivatives, Chemical & Pharmaceutical Bulletin, 2005, 53(9), p. 1136-1139.

23. Huang H. S., Chiu H. F., Tao C. W., Chen I. B., Synthesis and Antitumor Evaluation of Symmetrical 1,5-Diamidoanthraquinone Derivatives as Compared to Their Disubstituted Homologues, Chemical & Pharmaceutical Bulletin, 2006, 54(4), p. 458-464.

24. Ghose A. K., Crippen G. M., Atomic Physicochemical Parameters for Three-Dimensional Structure-Directed Quantitative Structure-Activity Relationships I. Partition Coefficients as a Measure of Hydrophobicity, Journal of Computational Chemistry, 1986, 7(4), p. 565-577.

25. Brändström A., Predictions of log P for aromatic compounds, J. Chem. Soc. Perkin Trans. 2, 1999, 11, p. 2419-2422.

26. Chuman H., Mori A., Tanaka H., Prediction of the 1-Octanol/H2O Partition Coefficient, Log P, by Ab Initio MO Calculations: Hydrogen-Bonding Effect of Organic Solutes on Log P, Analytical Sciences, 2002, 18(9), p. 1015-1020.

27. Hansch C., Leo A., Hoekman D., Exploring QSAR: Volume 2: Hydrophobic, Electronic, and Steric Constants, American Chemical Society Publication (ACS), Washington DC, 1995.

28. Young R. C., Development of a new physicochemical model for brain penetration and its application to the design of centrally acting H2 receptor histamine antagonists, J. Med. Chem., 1988, 31, p. 656-671.

29. Abraham M. H., Chadha H. S., Mitchell R. C., Hydrogen bonding. Part 33: Factors that influence the distribution of solutes between blood and brain, J. Pharm. Sci., 1994, 83, p. 1257-1268.

30. Salminem T., Pulli A., Taskinen J., Relationship between immobilized artificial membrane chromatographic retention and the brain penetration of structurally diverse drugs, J. Pharm. Biomed. Analysis, 1997, 15, p. 469-477.

31. Clark D. E., Rapid calculation of polar molecular surface area and its application to the prediction of transport phenomena. 2. Prediction of blood-brain barrier penetration, J. Pharm. Sci., 1999, 83, p. 815-821.

32. Luco J. M., Prediction of brain-blood distribution of a large set of drugs from structurally derived descriptors using partial least-squares (PLS) modelling, J. Chem. Inf. Comput. Sci., 1999, 39, p. 396-404.

33. Yazdanian M., Glynn S. L., In vitro blood-brain barrier permeability of nevirapine compared to other HIV antiretroviral agents, J. Pharm. Sci., 1998, 87, p. 306-310.

34. Grieg N. H., Brossi A., Xue-Feng P., Ingram D. K., Soncrant T. In: Greenwood J., et al, eds., New Concepts of a Blood-Brain Barrier, New York, NY: Plenum, 1995, pp. 251-264.

35. Lin J. H., Chen I., Lin T., Blood-brain barrier permeability and in vivo activity of partial agonists of benzodiazepine receptor: a study of L-663,581 and its metabolites in rats. J. Pharmacol. Exp. Ther., 1994, 271, p. 1197-1202.

36. Lombardo F., Blake J. F., Curatolo W., Computation of brain-blood partitioning of organic solutes via free energy calculations, J. Med. Chem., 1996, 39, p. 4750-4755.

37. Van Belle K., Sarre S., Ebinger G., Michotte Y., Brain, liver, and blood distribution kinetics of carbamazepine and its metabolic interaction with clomipramine in rats: a quantitative microdialysis study. J. Pharmacol. Exp. Ther., 1995, 272, p. 1217-1222.

38. Calder J. A. D., Ganellin R., Predicting the brain-penetrating capability of histaminergic compounds, Drug Design and Discovery, 1994, 11, p. 259-268.

39. Zhou Y., Sun Z., Froelich J. M., Hermann T., Wall D., Structure–activity relationships of novel antibacterial translation inhibitors: 3,5-Diamino-piperidinyl triazines, Bioorganic & Medicinal Chemistry Letters, 2006, 16(20), p. 5451-5456.

40. Zhou Y., Gregor V. E., Ayida B. K., Winters G. C., Sun Z., Murphy D., Haley G., Baily D., Froleich J. M., Fish S., Webber S. E., Hermann T., Wall D., Synthesis and SAR of 3,5-diamino-piperidine derivatives: Novel antibacterial translation inhibitors as aminoglycoside mimetics, Bioorganic & Medicinal Chemistry Letters, 2007, 17(5), p. 1206-1210.

41. Buckman A. H., Wong C. S., Chow E. A., Brown S. B., Solomon K. R., Fisk A. T., Biotransformation of polychlorinated biphenyls (PCBs) and bioformation of hydroxylated PCBs in fish, Aquatic Toxicology 2006, 78(2), p. 176-185.

42. Toropov A. A., Toropova A. P., QSAR modeling of toxicity on optimization of correlation weights of Morgan extended connectivity, Journal of Molecular Structure (Theochem), 2002, 578, p. 129-134.

43. Dong P.-P., Zhang Y.-Y., Ge G.-B., Ai C.-Z., Liu Y., Yang L., Liu C.-X., Modeling resistance index of taxoids to MCF-7 cell lines using ANN together with electrotopological state descriptors, Acta Pharmacol Sin, 2008, 29(3), p. 385-396.

44. Iyer M., Mishra R., Han Y., Hopfinger A. J., Predicting Blood-Brain Barrier Partitioning of Organic Molecules Using Membrane-Interaction QSAR Analysis, Pharmaceutical Research, 2002, 19(11), p. 1611-1621.

45. Bolboacă S. D., Ţigan S., Jäntschi L., Molecular Descriptors Family on Structure-Activity Relationships on anti-HIV-1 Potencies of HEPTA and TIBO Derivatives, Proceedings of the European Federation for Medical Informatics Special Topic Conference, 2006, pp. 222-226.

46. Opriş D. M., Diudea M. V., Peptide Property Modeling by Cluj Indices, SAR and QSAR in Environmental Research, 2001, 12(1-2), p. 159-179.

47. Clark D. E., Rapid Calculation of Polar Molecular Surface Area and Its Application to the Prediction of Transport Phenomena. 2. Prediction of Blood-Brain Barrier Penetration, Journal of Pharmaceutical Sciences, 1999, 88(8), p. 815-821.

48. Melagraki G., Afantitis A., Sarimveis H., Igglessi-Markopoulou O., Supuran C.T., QSAR study on para-substituted aromatic sulfonamides as carbonic anhydrase II inhibitors using topological information indices, Bioorganic & Medicinal Chemistry, 2006, 14(4), p. 1108-1114.

49. Xiao-lei M. A., Chen C., Yang J., Predictive model of blood-brain barrier penetration of organic compounds, Acta Pharmacologica Sinica, 2005, 26(4), p. 500-512.

50. Iyer M., Mishra R., Han Y., Hopfinger A. J., Predicting blood-brain barrier partitioning of organic molecules using membrane-interaction QSAR analysis, Pharm Res, 2002, 19, p. 1611-1621.

51. Balaban A. T., Khadikar P. V., Supuran C. T., Thakur A., Study on supramolecular complexing ability vis-à-vis estimation of pKa of substituted sulfonamides: Dominating role of Balaban index (J), Bioorganic & Medicinal Chemistry Letters, 2005, 15(17), p. 3966-3973.

52. Supuran C. T., Clare B. W., Carbonic anhydrase inhibitors - Part 57: Quantum chemical QSAR of a group of 1,3,4-thiadiazole- and 1,3,4-thiadiazoline disulfonamides with carbonic anhydrase inhibitory properties, European Journal of Medicinal Chemistry, 2002, 19(11), p. 1611-1621.

53. United States - National Library of Medicine – Chemical Information SIS Specialized Information Service. (online). © U.S. National Library of Medicine. Available from: URL: http://sis.nlm.nih.gov/chemical.html (accessed 09/07/09)

54. Morita H., Gonda A., Wei L., Takeya K., Itokawa H., 3d QSAR Analysis of Taxoids from Taxus Cuspidata Var. Nana by Comparative Molecular Field Approach, Bioorganic & Medicinal Chemistry Letters, 1997, 7(18), p. 2387-2392.

55. Thakur A., Thakur M., Khadikar P. V., Supuran C. T., Sudelea P., QSAR study on benzenesulphonamide carbonic anhydrase inhibitors: topological approach using Balaban index, Bioorganic & Medicinal Chemistry, 2004, 12, p. 789-793.

56. Mukherjee S., Mukherjee A., Saha A., QSAR Studies with E-State Index: Predicting Pharmacophore Signals for Estrogen Receptor Binding Affinity of Triphenylacrylonitriles, Biol. Pharm. Bull., 2005, 28(1), p. 154-157.

57. Cramer D., Basis Statistics for Social Research, Routledge, 1997, pp. 85.

58. Tabachnick B. G., Fidell L. S., Using Multivariate Statistics (3rd ed.), New York, HarperCollins, 1996, pp. 138-142.

59. EasyFit (2009) EasyFit: Distribution Fitting Software Math Wave Technologies, MA. Available from: URL: www.mathwave.com).

60. Pearson K., On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling, Philosophical Magazine, 1900, 50, p. 157-175.

61. Kolmogorov A., Confidence Limits for an Unknown Distribution Function, Annals of Mathematical Statistics, 1941, 12(4), p. 461-446.

62. Anderson T. W., Darling D. A., Asymptotic theory of certain "goodness-of-fit" criteria based on stochastic processes, Annals of Mathematical Statistics, 1952, 23(2), p. 193-212.

63. Jäntschi L., Bolboacă S. D., Distribution Fitting 2. Pearson-Fisher, Kolmogorov-Smirnov, Anderson-Darling, Wilks-Shapiro, Cramer-von-Misses and Jarque-Bera statistics, Bulletin of University of Agricultural Sciences and Veterinary Medicine Cluj-Napoca. Horticulture, 2009, 66(2):691-697 ( http://arxiv.org/abs/0907.2832).

64. Grubbs F., Procedures for Detecting Outlying Observations in Samples, Technometrics 1969, 11(1), p. 1-21.

65. Yao C., Levy R. H., Inhibition-based metabolic drug-drug interactions: Predictions from in vitro data, Journal of Pharmaceutical Sciences, 2002, 91(9), p. 1923-1935.

66. Copeland R. A., Enzymes: A practical introduction to structure, mechanism and data analysis, Wiley-VCH, NY, 2nd Edition, 2000.

67. Abraham M. H., Chadha H. S., Mitchell R. C., Hydrogen bonding. Part 36. Determination of blood-brain barrier distribution using octanol-water partition coefficients, Drug Des. Discov. 1995, 13, p. 123-131.

68. Doucette W. J., Soil and Sediment Sorption Coefficient, In: Boethling RS, Mackay D (eds). Handbook of Property Estimation Methods for Chemicals, Environmental and Health Sciences. Lewis Publishers, 2000, 141-188.

69. Hill J. W., Petrucci R. H., General Chemistry, 2nd edition, Prentice Hall, 1999.