Modeling the Physical Properties of Popcorn Varieties as a Function of Kernel Moisture Content
Falilat Taiwo ADEMILUYI1*, Koyejo ODUOLA2
1Department of Chemical/Petrochemical Engineering, Rivers State University of Science & Technology, Port Harcourt, Nigeria
2Department of Chemical Engineering, University of Port Harcourt, Nigeria
E-mails: ademuluyi@yahoo.com, koye_oduola@yahoo.com
*Corresponding author: Phone: 08034561089
Received: 28 September 2010 / Accepted: 13 May 2011 / Published: 25 June 2011
Abstract
The physical properties such as the axial dimensions (length, width, thickness), geometric mean diameter, thousand kernel weight, shape characteristics (sphericity, kernel volume, kernel surface area), bulk density, particle or kernel density, as well as porosity have been evaluated as a function of kernel moisture content for “pin” and “deep” yellow varieties of Nigerian popcorn kernels. It has been observed that the length, width, thickness as well as the thousand kernel weight increase with increasing moisture content for both varieties under investigation in the moisture range 11-17% (wet basis.), while the bulk and particle densities together with the kernel porosity have been found to decrease with increasing moisture content. These physical properties vs moisture content dependencies have been fitted to linear, polynomial and other non-linear equations and the empirical constants determined for each case. Regression analyses have revealed that the third-order polynomial and quadratic functions more adequately describe the observed dependencies than the linear equation in most cases, based on the resulting correlation coefficients and standard errors.
Keywords
Correlation Coefficient; Moisture Content; Physical Properties; Popcorn Varieties.
Introduction
The determination of physical properties of agricultural products becomes imperative to obtain the essential engineering data in the design and development of systems and machines, structures, processes and controls. In addition, these properties are important to analyze and determine the theoretical performance, heat/power requirements and efficiencies of machines or operations used in the handling and processing of grains [1].
In particular, the sphericity and physical dimensions are applicable in the design of pneumatic or electrostatic machines that separate grains from admixtures [1]. Tado [2] employed the sphericity and geometric mean diameter (GMD) for the determination of aerodynamic properties such as terminal velocity, drag coefficient and Reynolds number and for the design of fluidized bed drier and winnower.
The bulk and particle densities of grains have found applicability in the design of silos and storage bins, specific gravity separators as well as in the grading of grains for price fixing, while the porosity of grains is imperative in airflow, heat flow and drying investigations, especially for determining the Reynolds number in pneumatic and hydraulic handling of grains, and in calculating thermal diffusivity in drying and other heat transfer problems.
The moisture dependence of the physical properties of various grains and pulses has been studied by many researchers [3-5]. Nalladurai [6] have found that the physical dimensions (length, width and thickness as well the geometric mean diameter GMD), thousand grain weight, bulk and particle density, porosity, angle of repose and coefficient of friction on GI and plywood surfaces determined for raw paddy, parboiled paddy, raw rice and parboiled rice varieties all increased with increasing moisture levels. On the contrary, however, a number of researchers have established the negative linear relationship of certain physical properties including the bulk density, true density and porosity with the moisture levels.
Simulation of the physical properties vs moisture content dependencies of popcorn kernels will be of importance in the control/improvement of the popping characteristics (especially expansion volume which is the most important factor influencing the kernel economic value [1]. or process control. Physical properties including the kernel size, sphericity, density and test weight have been found to exert profound influence on the popping properties of popcorn kernels [7, 8]. Previous attempts on studying these dependencies have shown contradictory and inconclusive results due to differing moisture contents, varieties, measurements and experimental conditions [8]. Even though, there were several attempts to fit the physical properties vs moisture content data to mathematical equations (Ersan, 2006), no convincing basis for the equations used was given and the results presented appeared contradictory and uncorrelated.
Different varieties of popcorn are now grown in Nigeria, and packaged as over dried popcorn in Hessian bags for preservation and not easily ready for use like the imported type. Besides, variability in the physical characteristics of the Nigerian and imported popcorn hybrids certain functional (poppability) nutritive and organoleptic properties might influence characteristics of the popcorn varieties. Physical properties of kernels, grains and seeds are necessary for the design of equipment to handle, transport, process and store the crop raw material [10] and to define and quantify heat study was to transfer problems during heat processing of seeds.
Previous work [11] showed that the Nigerian popcorn hybrids (deep yellow and pin type) are rich in carbohydrate (60.6-64.0%), protein (8.3-8.7%) and fat (6.6-8.8%). The high fiber content also makes Nigerian popcorn crispier than the foreign type. The overall acceptance of the Nigerian popcorn from sensory evaluation conducted in this study [12] showed that the Nigerian popcorn could favorably compete with other foreign type in the export market especially the pin and deep yellow popcorn varieties.
Therefore, the objective of this investigate the physical properties such as the axial dimensions (length, width, thickness), geometric mean diameter, thousand kernel weight, shape characteristics (sphericity, kernel volume, kernel surface area), bulk density, particle or kernel density, as well as porosity of two predominant varieties of popcorn kernels: yellow Pin and Deep yellow varieties at various moisture levels. The results obtained will be used for obtaining mathematical models describing the dependence of each property on the moisture content.
Materials and Methods
The parameters investigated were: moisture content, size (length, width and thickness), thousand kernel weight, particle density and bulk density, while the geometric mean diameter, porosity, sphericity, kernel volume and surface area were evaluated from these data. Measurements were carried out in the laboratory at normal room temperature and relative humidity of 27°C and 55 % respectively.
Two popcorn varieties investigated were obtained from the Ahmadu Bello University Zaria in the Northern part of Nigeria. They are: yellow Pin (rice shaped) and Deep yellow varieties (oval shaped), which upon harvesting were sun-dried and stored in bags prior to purchase. The kernels (initially containing about 12.8-13.8 % moisture) were cleaned prior to investigation manually to remove all foreign matter and broken kernels, and then conditioned to specific moisture contents by adding a calculated amount of water (or drying), mixing thoroughly and then sealing in separate polyethylene bags. The samples were conditioned in a refrigerator at 5°C for 7 days for the moisture to distribute uniformly, and the required quantities were removed from the refrigerator and allowed to warm up to room temperature prior to investigations. Some were dried down to 11 % moisture content in an oven at a temperature of 60°C and relative humidity of 55 %. The moisture content of popcorn kernels was determined with the aid of Delm Horst Grain moisture detector (G-7).
The length (L, the distance from the tip crown to the kernel crown), width (W, the widest point-to-point measurement taken parallel to the face of the kernel) and thickness (T, the distance between the two kernel faces) constitute the axial dimensions of popcorn kernels [9]. Thirty samples of popcorn kernels of the pin and deep varieties were randomly selected from each of the moisture contents under test and the physical dimensions of each kernel were determined by measurement using Vernier Caliper with a least count of 0.02 mm.
The geometric mean diameter (GMD), Dg, the sphericity (the shape factor of the kernels relative to that of a sphere of equal volume, S), as well as the kernel volume (V), and surface area (A), were calculated using the following expressions [1, 4].
|
GMD = Dg = (LWT)1/3 |
(1) |
|
S = SWT1/3/L |
(2) |
|
V = πB2L2/6(2L –B) |
(3) |
|
A = πBL2/(2L –B) |
(4) |
where the diameter of the kernel spherical part,
|
B = (WT)˝ |
(5) |
Determination of the thousand kernel weight (M1000) was carried out by randomly selecting 100 kernels of each sample into a container and weighing in a digital electric balance. The weight of container was subtracted from the total weight of kernel plus container and the M1000 was then computed by multiplying M100 by ten.
Particle Density Dp of popcorn kernels was determined from the specific gravity by means of pycnometer method based on Archimedes principle of liquid displacement. Popcorn samples of known weight were immersed in a measuring cylinder containing 50 ml of toluene and the particle density of each sample was calculated by dividing the mass of sample by the volume of toluene displaced by the popcorn kernel. Evaluation of the popcorn kernel Bulk Density Db was conducted by using a cylinder of about 230 cm3 capacity which was initially weighed empty. The samples were charged instantaneously into the cylinder with the excess sample at the top tapped and the weight of content and cylinder was recorded using an electronic balance (Mettler P1210) with 0.01 g accuracy. The bulk density was calculated from the weights divided by the volume of the popcorn kernels in the cylinder.
The porosity P of popcorn samples was calculated from the Db and Dp data using the following expression:
|
P = (1 –Db/Dp)×100 |
(6) |
The physical properties vs moisture ratio data were fitted to linear, polynomial and other non-linear equations by employing a non linear regression package, Data fit (Oakdale Engineering Software, http://www.curvefitting.com) version 8.2.79. In addition to coefficient of correlation (R2), the goodness of fit was determined by the root mean square error (RMSE, Standard Error) and the best fits were obtained using the model equations presented in Table 1-5. For quality fit, R2 value should be higher, while RMSE should be lower [13, 14].
Results and Discussions
The physical properties determined for a number of samples were processed with the aid of Microsoft Excel software to obtain the mean values, standard deviations and confidence intervals. The resulting mean values were matched with the corresponding moisture contents for further analyses, interpretation and processing.
Physical Dimensions
All the axial dimensions (L, W, T) as well as the GMD, sphericity, surface area and volume of popcorn kernels have been found to increase with an increase in the moisture content (Figures 1-2) with the exception of the sphericity values for deep yellow varieties where an anomalous dependence was obtained.
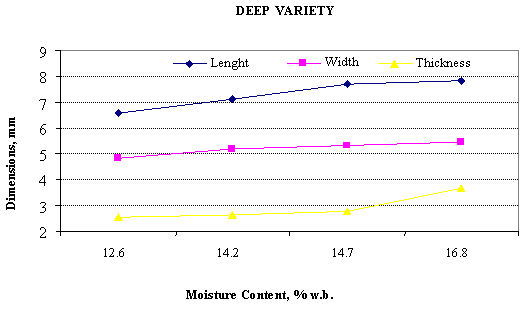
Figure 1. Effect of moisture content on the axial dimensions of the deep yellow varieties of popcorn kernels
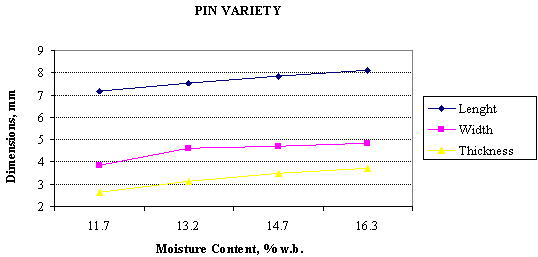
Figure 2. Effect of moisture content on the axial dimensions of the pin varieties of popcorn kernels
Evident is the fact that kernels expand in all the axial dimensions within the moisture range 11-17% with the average expansion in the order ∆T (41.6%) > ∆W (25.8%) > ∆L (13.1%) for the pin varieties and ∆T (45.4%) > ∆L(18.7%) >∆W (13.1%) for the deep yellow varieties. The latter dependences correlate well with the data reported by Ersan [4]. The coefficient of correlation and results of statistical analyses are listed in Tables 1 and 2, indicating that the Length L, Width W, Thickness T vs. moisture content are best fitted to the quadratic functions and least by the linear dependencies. In majority of the cases, the GMD, kernel volume as well as the sphericity also yielded R2 values > 0.95 with quadratic functions, indicating a good fit.
Table 1. Regression variable results of modeling the length (L), width (W) and thickness (T) for pin and deep yellow varieties
|
Model |
L-pin |
L-deep |
||||
|
Model constants |
StdError |
R2 |
Model constants |
StdError |
R2 |
|
|
Y = a*x^2+b*x+c |
a=-0.0117, b=0.5319, c=2.5277 |
0.0012 |
1 |
a=-0.0684, b=2.3164, c= -11.7653 |
0.2927 |
0.9114 |
|
Y = a+b*log(x) |
a=0.1684, b=2.8422 |
0.0146 |
0.9991 |
a=-4.4966, b=4.4143 |
0.2718 |
0.8472 |
|
Y = a*x+b |
a=0.2043, b=4.7869 |
0.0391 |
0.9938 |
a=0.2972, b=2.9763 |
0.2926 |
0.8229 |
|
|
W-pin |
W-deep |
||||
|
Y = a*x^2+b*x+c |
a=-0.0703, b=2.1690, c=-11.8957 |
0.1435
|
0.9659
|
a=-0.0384, b=1.2802, c=-5.2201 |
0.0389
|
0.9932
|
|
Y = a+b*log(x) |
a=-3.0076, b=2.8502 |
0.2331 |
0.8198 |
a=-0.6667, b=2.1930 |
0.1043 |
0.9028 |
|
Y = a*x+b |
a=0.2008, b=1.6814 |
0.2558 |
0.7829 |
a=0.1473, b= 3.0507 |
0.1193 |
0.8729 |
|
|
T-pin |
T-deep |
||||
|
Y = a*x^2+b*x+c |
a=-0.0301, b=1.0792, c=-5.8939 |
0.0068
|
0.9999
|
a=0.0749, b=-1.9291, c=14.9384 |
0.0083
|
0.9999
|
|
Y = a+b*log(x) |
a=-5.4903, b=3.3161 |
0.0721 |
0.9847 |
a=-7.9313, b=4.0543 |
0.2559 |
0.8406 |
|
Y = a*x+b |
a=0.2373, b=-0.0860 |
0.1006 |
0.9702 |
a=0.2825, b=-1.2081 |
0.2266 |
0.8750 |
Table 2. Regression variable results of modeling the geometric mean diameter (GMD), kernel volume (V), surface area (A), as well as the sphericity (S) for pin and deep yellow varieties
|
Model |
GMD-pin popcorn |
GMD-deep yellow popcorn |
|||||
|
Model constants |
StdError |
R2 |
Model constants |
StdError |
R2 |
||
|
Y = a+b/x+c/x^2 |
a=2.8500, b= 98.556 c=-975.97 |
0.0247 |
0.9991
|
a=19.241, b= 368.64 c=2274.7 |
0.1415
|
0.9677 |
|
|
Y = a*x^2+b*x+c |
a=-0.0425, b= 1.4210 c=-6.6635 |
0.0483 |
0.9965
|
a=0.0357, b=-0.8010 c=8.7347 |
0.1324
|
0.9717 |
|
|
Y = a+b*x^3 +c*exp(x) |
a=3.1464, b=6.58E-4 c=-6.45E-8 |
0.1323 |
0.9740 |
a=3.7949, b= 2.26E-4 c=1.7E-8 |
0.1214
|
0.9762 |
|
|
Y = a*x+b |
a=0.2319, b=1.5392 |
0.1459 |
0.9366 |
a=0.2533, b=1.0375 |
0.1429 |
0.9340 |
|
|
|
V-pin |
V-deep |
|||||
|
Y = a*x^2+b*x+c |
a=-0.8389, b= 29.314 c=-203.81 |
0.8041
|
0.9984
|
a=0.9437, b=-20.806 c=140.81 |
1.3733
|
0.9959
|
|
|
Y = a+b*log(x) |
a=-174.42, b=81.365 |
2.1686 |
0.9772 |
a=-232.70, b= 102.04 |
3.7185 |
0.9406 |
|
|
Y = a*x+b |
a=5.8144, b=-41.712 |
2.8607 |
0.9603 |
a=7.0452, b=-62.526 |
3.0139 |
0.9610 |
|
|
|
A-pin |
A-deep |
|||||
|
Y = a*x^2+b*x+c |
a= -0.9247, b= 31.682 c=-198.18 |
0.9477
|
0.9978
|
a=0.5353, b=-9.0131 c=77.5580 |
1.9694
|
0.9908
|
|
|
Y = a+b*log(x) |
a= -151.66, b=80.974 |
2.4752 |
0.9702 |
a=-202.63, b= 98.628 |
2.7164 |
0.9652 |
|
|
Y = a*x+b |
a= 5.7803, b=-19.504 |
3.1621 |
0.9514 |
a= 6.7834, b=-37.765 |
2.1349 |
0.9785 |
|
|
|
S-pin |
S-deep |
|||||
|
Y = a+b/x+c/x^2 |
a= 0.1421, b=16.169 c=-129.10 |
0.0064
|
0.9860
|
a= 2.2749, b=-45.242 c=312.32 |
0.0177
|
0.8358 |
|
|
Y = a*x^2+b*x+c |
a= -0.0043, b=0.1360 c=-0.4142 |
0.0091 |
0.9717 |
a=0.0066, b=-0.1863 c=1.9455 |
0.0162
|
0.8613
|
|
|
Y = a+b*x^3 +c*exp(x) |
a= 0.5124, b=4.7E-05 c=-5.5E-09 |
0.0165 |
0.9060 |
a=0.6928, b=-2.1E-05 c=4.9E-09 |
0.0131
|
0.9101
|
|
Thousand Kernel Weight
The thousand kernel weight of popcorn kernels has been found to increase from 116.3 g to 126.2 g and 128.4 g to 135.0 g respectively for the pin and deep varieties within the investigated moisture range. The regression variable results (Table 3) show that the highest values of R2 and lowest values of RMSE were obtained with the third order polynomial functions, while linear fits of the weight vs. moisture levels dependence yielded relatively lower correlation coefficients and higher standard errors for both deep and pin popcorn varieties.
Table 3. Regression variable results of modeling the thousand kernel weight for
Pin (M1000-pin) and deep yellow (M1000-deep) varieties
|
Model |
M1000-pin |
M1000-deep |
||||
|
Model constants |
StdError |
R2 |
Model constants |
StdError |
R2 |
|
|
Y = a*x^3+ b*x^2+c*x+d |
a=0.3109, b=12.9112 c=-174.91, d=893.24 |
1.1919
|
0.9784
|
a=0.0128, b=0.4113 c=-2.5190, d=122.09 |
0.2122
|
0.9968
|
|
Y = a*x^2+b*x+c |
a=-0.1453, b=6.3625, c=61.346 |
1.3441
|
0.9451
|
a=-0.1365, b=5.2019 c=86.149 |
0.1814
|
0.9965
|
|
Y = a+b*log(x) |
a=37.5685, b=31.917 |
1.1233 |
0.9425 |
a=82.980, b=18.564 |
0.3410 |
0.9836 |
|
Y = a*x+b |
a=2.2938, b=89.4924 |
1.1873 |
0.9358 |
a=1.3033, b=113.59 |
0.4831 |
0.9671 |
Bulk and Particle Densities
The bulk and particle densities of popcorn kernels for both deep and pin varieties have been observed to decrease with increasing moisture content (Figures 3 and 4). These results imply that the rate of increase of the kernel volume is much higher than that of its weight as the moisture level rises. In fact, the kernel volume rises by over 100% while the weight increases by only 5-8% within the moisture content range 11-17%.
Contradictory results were reported for raw paddy, parboiled paddy, raw rice and parboiled rice varieties whose bulk and particle densities all increased with increasing moisture levels [6], while similar trends of linear decrease of the true and bulk densities from 1.304 to 1.224 g/cm3 and 0.771 to 0.703 g/cm3 respectively were obtained for foreign popcorn kernels with moisture content increasing in the range 8.95% to 17.12% (db) [4]. The third order polynomial function alongside with the quadratic, linear and first order logarithmic functions have all been found to be especially adequate (with high R2 values and low standard errors) for predicting both the bulk and particle densities of popcorn varieties (Table 4).
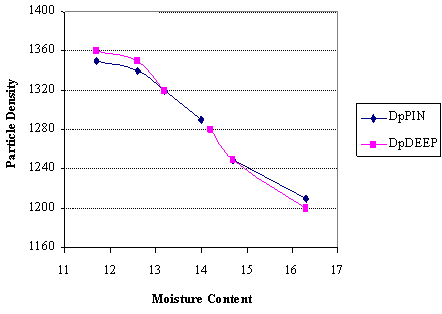
Figure 3. Effect of moisture content on the particle density of the pin and deep yellow varieties where DpPIN = particle density of the pin , DpDEEP = particle density of the deep yellow
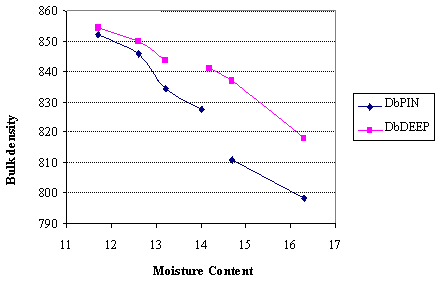
Figure 4. Effect of moisture content on the bulk density of the pin and deep varieties of popcorn kernels where DpPIN = particle density of the pin , DpDEEP = particle density of the deep yellow
Table 4. Regression variable results of modeling the bulk density (Db) and particle density (Dp) for pin and deep varieties
|
Model |
Db-pin |
Db-deep |
||||
|
Model constants |
StdError |
R2 |
Model constants |
StdError |
R2 |
|
|
Y = a*x^3+ b*x^2+c*x+d |
a=0.8888, b=-37.153 c=501.17, d=-1349.1 |
3.5022
|
0.9885
|
a=-0.5002, b=20.072 c=-273.33, d=2106.3 |
1.7591
|
0.9925
|
|
Y = a*x^2+b*x+c |
a=0.1416, b=-16.476, c=1027.58 |
4.1440
|
0.9758
|
a=-0.9485, b=18.919 c= 762.14 |
2.2499
|
0.9816
|
|
Y = a*x+b |
a=-12.505, b=1000.07 |
3.6093 |
0.9755 |
a=-7.6444, b=945.95 |
3.2170 |
0.9499 |
|
Y = a+b*log(x) |
a=1282.05, b=173.56 |
3.7303 |
0.9739 |
a=1115.3, b=-104.94 |
3.8139 |
0.9296 |
|
|
Dp-pin |
Dp-deep |
||||
|
Y = a*x^3+ b*x^2+c*x+d |
a=3.2461, b=-137.47 c=1893.0, d=-7178.7 |
3.9123
|
0.9980
|
a=2.9279, b=-124.16 c=1704.5, d=-6274.9 |
4.8810
|
0.9975
|
|
Y = a*x^2+b*x+c |
a=-1.2667, b=2.4952, c=1501.31 |
11.4102
|
0.9738
|
a=-1.1071, b=-6.3552, c=1593.7 |
10.8927
|
0.9814
|
|
Y = a*x+b |
a=-33.020, b= 1747.4 |
10.4592 |
0.9707 |
a=-37.3588, b=1808.3 |
9.8952 |
0.9795 |
|
Y = a+b*log(x) |
a=2487.07, b=456.45 |
12.0414 |
0.9612 |
a=2644.8, b= -516.30 |
11.6651 |
0.9716 |
Porosity
Being a derivative of the bulk and particle density of the popcorn kernels, the porosity has also been found to decrease with increasing moisture levels due to the reasons described above. The decrease in porosity however has been found to be more profound for the deep (14.2%) than for the pin variety (7.9%). Regression analysis of modeling the porosity vs. moisture content dependencies for both deep and pin varieties (Table 5) have followed similar trends with their bulk and particle density values, wherein the porosity values can conveniently be predicted by the third order polynomial function alongside with the quadratic, linear and first order logarithmic functions.
Table 5. Regression variable results of modeling porosity for pin (P-pin) and deep (P-deep) varieties
|
Model |
P-pin |
P-deep |
||||
|
Model constants |
StdError |
R2 |
Model constants |
StdError |
R2 |
|
|
Y = a*x^3+ b*x^2+c*x+d |
a=0.0902, b=-3.8690 c=54.203, d=-212.10 |
0.1383
|
0.9946
|
a=0.1741, b=-7.3213 c=100.54, d=-415.77 |
0.1164
|
0.9989
|
|
Y = a*x^2+b*x+c |
a=-0.0850, b=1.6827 c=29.044 |
0.3246
|
0.9553
|
a=-0.00333, b=-1.2045 c= 52.176 |
0.6103
|
0.9529
|
|
Y = a*x+b |
a=-0.7014, b=45.561 |
0.3633 |
0.9253 |
a=--1.2978, b=52.821 |
0.5286 |
0.9529 |
|
Y = a+b*log(x) |
a=61.102, b=-9.6302 |
0.4121 |
0.9039 |
a=81.968, b=-17.968 |
0.5520 |
0.9486 |
Conclusions
The axial dimensions (length, width, thickness), geometric mean diameter as well as the shape factors (sphericity, kernel volume, kernel surface area) have been found to increase with increasing moisture content for both “pin” and “deep” yellow varieties of popcorn kernels in the moisture range 11-17% (dry basis). The axial dimensions are best fitted to the quadratic functions and least by the linear dependencies. In majority of the cases, the geometric mean diameter, kernel volume as well as the sphericity also yielded R2 values > 0.95 with quadratic functions, indicating a good fit. The thousand kernel weight has also been shown to increase with increasing moisture content with the highest values of R2 and lowest values of RMSE obtained by modeling with the third order polynomial functions, while linear fits of the weight dependence on moisture levels yielded relatively lower correlation coefficients and higher standard errors for both deep and pin popcorn varieties.
The bulk and particle density, as well as porosity have been found to decrease with increasing moisture content apparently due to the higher rate of increase of the kernel volume than that of its weight as the moisture level rises. Regression analyses have revealed that the third-order polynomial alongside with the quadratic, linear and first order logarithmic functions are all especially adequate (with high R2 ≥ 0.95 in most cases) for predicting both the bulk and particle densities and porosities of popcorn varieties.
References
1. Mohsenin N.N., Physical properties of plant and animal materials, Gordon and Breach publishers, New York, 1980.
5. Kaleemullah S., Gunasekar J.J., Moisture-dependent Physical Properties of Arecanut Kernels, Biosystem Engineering, 2002, 2(3) p. 331-338
8. Allred-Coyle T.A., Toma R.B., Reiboldt W., Thakur M., Effects of moisture content, hybrid variety, kernel size, and microwave wattage on the expansion volume of microwave popcorn, International Journal of Food Sciences and Nutrition, 2000, 51(5), p. 389-394.
9. Pordesimo L.O., Anantheswaran R.C., Fleischman A.M., Lin Y.E., Hanna M.A., Physical properties as indicators of popping characteristics of microwave popcorn. Journal of Food Science, 1990, 55, p. 1352-1355.
10. .Shimoni E, Dirks E.M, Labuza T.P., The relation between final popped volume of popcorn and thermal-physical parameters, Lebensmitter-Wisssenschaft and Technologies, 2002, 35(1); p. 93-98.