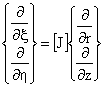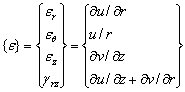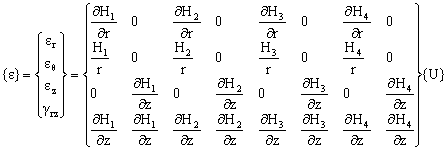Development of Finite Element Response Model for Mechanistic - Empirical Design of Flexible Pavement

Mujtaba A. AHMED, Hassan S. OTUOZE^*, and Abdulfatai A. MURANA

Dept. of Civil Engineering, Ahmadu Bello University, Zaria, Nigeria

E-mail(s): hassanotuoze@yahoo.com, elmuj4real@yahoo.co.uk, fatinoyi2007@yahoo.com

^* Corresponding author: Phone: +238032895989  

Abstract

The focus of this work is to present a finite element method (FEM)-based program of the M-E design on MATLAB protocol. The response output generated at critical locations are presented. The results were then compared with those from a locally available program called ‘NEMPADS’ and a reasonable comparison were achieved.

Keywords

Mechanistic-Empirical; Finite Element Method; MATLAB; ‘Ahmadu Bello University-Pavement (ABU-PAVE); Nigeria Empirical and Mechanistic Pavement Analysis and Design System (NEMPADS).

Introduction

Accurate pavement performance prediction is widely recognized by pavement community as one of the most important and difficult task to pursue. Proper selection of pavement materials and layers thicknesses can be optimized based upon performance–based specifications. The basic requirement for this is the availability of accurate pavement performance prediction methodology [1].

The state-of-the-art in flexible pavement design is manifested in mechanistic-based design methods in that it incorporates the treatment of life-cycle costs and design reliability in their design procedures. These techniques use pavement response in terms of stresses and strains as a major causative factors affecting pavement performance, which are directly related to the pavement layer material properties [2].

M-E method of flexible pavement design is an emerging technology for design which contains a number of distress models, mainly fatigue cracking and rutting, which are used to determine the design life of pavement [3]. With the current state of knowledge, the estimation of stresses and strains can be estimated by theory of elasticity for linear analysis and is termed as Layered Elastic Analysis (LEA) [4]. This analysis may or may not be accurate since in actual situation, most of the paving materials, especially the unbound material, behaves non-linearly under load and thus cannot be properly characterized by linear analysis. Several techniques have been used in the past to characterize non-linear nature of the unbound material; however the most common of these techniques is the Finite Element Method (FEM). With Finite Element Analysis, it is possible to treat non-linear elastic materials through an iterative process. Because of the complex mathematical computational nature of this analysis, limited number of programs, based on this methodology had been developed in the past for characterizing the non-linear behaviour of pavement layers. Other programs in this category are Finite Difference Methods, e.g. FLAC, etc., Boundary Element Methods, e.g. BEASY, etc. Examples of Finite Element Programs are MICH-PAVE and ILLI-PAVE. With the advent of the fast computers and reduced processing times, finite element analysis is becoming more popular [5].

The research is aimed at developing a pavement performance response model best suited to Nigerian environment to predict, to an acceptable degree of accuracy, the distresses, namely – stresses, strains and deformations in flexible. This is because most Mechanistic-Empirical softwares are developed adaptable to specific environments or conditions of the location of their designers. Among the leading examples are ILLI-PAVE (University of Illinois), DSC2D (University of Arizona), DYNA (Livermore Software Technology Corporation), JULEA (Jacob Uzea Layered Elastic Analysis) etc and hence, the reason to have ABU-PAVE (Ahmadu Bello University, Zaria, Nigeria) which is adapted to Nigerian environment.

Material and Method

Finite Element Method

Finite element method is based on discrete element idealization. The domain of the problem is subdivided into sub-domains of which pavement layers are an example. These sub-domains are discredited into a number of finite-sized elements. These finite elements are subsequently interconnected by nodes at their common edges and assembly of all these elements will represent the problem for general analysis [6, 13].

In many phases of engineering, the solution of stress and strain distribution in elastic continua is required. Special cases of problems may range from 2-D plane stress or strain distribution, axisymmetrical solids, plate bending, and shell, to fully 3-D solids. In all cases the number of interconnections between any ‘finite element’ isolated by some imaginary boundaries and the neighbouring elements is infinite. It is therefore difficult to see how such problems may be discredited. However, the difficulty can be overcome (and approximation made) in the following manner [6]:

· The continuum is separated by imaginary lines or surfaces into a number of ‘finite elements’.

· The elements are assumed to be interconnected at a discrete number of nodal points situated on their boundaries; the displacements of these nodal points will be the basic unknown parameters of the problem.

· A set of functions is chosen to define uniquely the state of displacement within each ‘finite element’ in terms of its nodal displacements.

· The displacement functions now define uniquely the state of strain within an element in terms of nodal displacements; these strains, together with any initial strains and constitutive properties of the material will define the state of the stress throughout the element and, hence, also on its boundaries.

· A system of stress concentrated at the nodes and equilibrating the boundary stresses and distributed loads is determined resulting in stiffness relationship of the form shown below:

{F}^a = [K]^a{δ}^a + {F}^ap + {F}^as0

(1)

where:  {F}^a_p = nodal forces required to balance any distributed load acting on the element, {F}^a_s0= nodal forces required to balance any initial strains such as may be caused by temperature change if the nodes are not subjected to any displacement. The first term represents the forces induced by displacement of the nodes.

 Following these, four general FEM procedures are applied:

1. Determination of elements properties from the geometric material and loading data: for each element, the stiffness matrix and the corresponding nodal loads are found from the equation (1.0) above.

2. Assembly of final equations of the type given below:

[K]{δ} = {R} – {F}p – {F}s0

(2)

1. Insertion of prescribed boundary conditions into the final assembled matrix.

2. Solving the resulting equation system.

Clearly, a series of approximations has been introduced. Firstly, it is not always easy to ensure that the chosen displacement functions will satisfy the requirement of displacement continuity between adjacent elements. Thus, the compatibility conditions on such lines may be violated (though within each element it is obviously satisfied due to uniqueness of displacements implied in their continuous representation). Secondly, by concentrating the equivalent forces at the nodes, equilibrium conditions are satisfied in overall sense only. Local violation of equilibrium conditions within each element and on its boundaries will usually arise.

In general, the finite element procedures can analyse the non-linear pavement systems more realistically than other structural models by considering the variation of modulus within each layer. The stress-dependent properties in the form of resilient modulus MR and the failure criteria for granular materials and fine-grained soils were incorporated in this methodology. The principal stresses in the granular and/or subgrade layer are modified at the end of each iteration in a way whereby they do not exceed the strength of the materials, as defined by the Mohr-Coulomb failure envelop (12).

Axisymmetric Finite Element Analysis

(3) Formulates the plane linear isoparametric element which can be revised to obtain the axisymmetric element. A typical axisymmetric cross section is shown in Figure 1. The global coordinates (radial and vertical), and the corresponding displacements at an internal point can be related to the corresponding nodal quantities through shape functions [6-9]:

and

(3)

where {C}^T={r₁z₁r₂z₂r₃z₃r₄z₄}= nodal coordinates, {U}^T={u₁v₁u₂v₂u₃v₃u₄v₄}= nodal displacements.

The shape function matrix is given as:

(4)

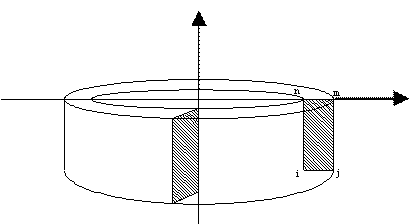
Figure 1. Typical Axisymmetric Finite Element Shape

The individual shape functions are:

H2(ξ, η) = 0.25(1 – ξ)(1 – η)	(5)
H2(ξ, η) = 0.25(1 + ξ)(1 – η)	(6)
H2(ξ, η) = 0.25(1 + ξ)(1 + η)	(7)
H2(ξ, η) = 0.25(1 – ξ)(1 + η)	(8)

In order to compute the derivative of this bilinear isoparametric element, we apply chain rule. Or simply in matrix form:

,

(9)

The components of the Jacobian matrix are computed as shown below:

	(10)
	(11)
	(12)
	(13)

Substitution of bilinear shape functions into the above equations (10-13) yield:

J11 = H1,ξr1+H2,ξr2+H3,ξr3+H4,ξr4

(14)

There are similar expressions for J12, J21, and J22; where:

H1,ξ = – 0.25(1 – η)	(15)
H1, η = – 0.25(1 – ξ)	(16)

The relationships between strain and displacement vectors are:

(17)

The above strain-displacement relationship is better written in linear form thus:

{ε} = [B]{U}

(18)

Or thus:

(19)

Where [B] is known as the kinematic matrix. The element stiffness matrix is:

[K^e] = ∫∫∫v[B]^T[D][B]rdrdθdz = ∫∫[B]^T[D][B]rdrdz

(20)

Or:

[K^e] = 2π∫-1^1∫-1^1[B]T[D][B]r[J]dξdη

(21)

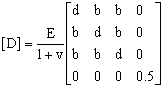
Where the matrix of elastic constant (the constitutive matrix) [D] is:

(22)

where:

d = (1 – v)/(1 – 2v); b = v/(1 – 2v)

(23)

Equation (21) must be integrated numerically. Using Gauss quadrate in two dimensions, the integral of a function Φ (ξ, η) can be expressed as:

[K^e] = ∫-1^1∫-1^1Φ(ξ,η)dξdη – ∑∑WiiWjiΦ(ξ,η)

(24)

where W_i and W_j are weights associated with the Gauss-points (ξ_i,η_j).

Formulation of Edge Loads

The edge loads applied along the upper edge of an element need to be transformed into equivalent nodal load. This is performed by integrating along the surface S thus:

fs = ∫SH^TSdS

(25)

where fs is the forces along surface. Changing to natural coordinate, the radial and vertical nodal loads can be expressed as:

	(26)
	(27)

where P_n= normal load; P_t = tangential load.

In pavement analysis, wheel loads are considered to act vertically and hence P_t = 0. Therefore equations (26) and (30) reduce to:

(28)

Since  for local and global axes in the same direction (as in this case):

(29)

Using Gaussian quadrature, one dimensional integration of a function Φ (ξ) becomes:

(30)

where W_i = the weight associated with the Gauss-point ξ_i.

Nonlinear Model: The Resilient Modulus

The resilient modulus (M_R) is a measure of the elastic property of a soil recognizing certain nonlinear characteristics. It is readily useful in mechanistic analysis for the prediction of cracking, rutting etc. [5].

In pavement, repeated vehicle loads cause permanent deformations as well as resilient (recoverable) deformations. In practice, mechanistic models are used only to compute stresses and resilient strain, while permanent (plastic) deformation is empirically related to the resilient strains, magnitude of load, number of load applications, material properties, etc. The resilient response is characterized by modulus material, which is defined as the ratio of the repeated axial deviator stress to the recoverable axial strain.

For the granular base and sub-base materials, the resilient modulus can be expressed in terms of the bulk stress as follows [5]:

(31)

where: M_r=resilient modulus, θ=bulk stress(σ1+σ2+σ3), K1,K2 = experimental test constants.

The Finite Element Program

The practical use of finite element analysis is based on matrix algebra and the use of electronic computer, because it is only in matrix form that the complete solution process can be expresses in a compact and elegant manner [8].

In general, MATLAB is a useful tool for vector and matrix manipulations. Since the majority of the engineering systems are represented by matrix and vector equations, we can relieve our workload to a significant extent by using MATLAB [10, 14]. The FEM is a well-defined candidate for which MATLAB can be very useful as a solution tool, because matrix and vector manipulations are essential parts in the method.

The program developed in this research named ‘ABU-PAVE’, considers the base and sub-base materials as nonlinear. The AC and subgrade layers are considered linear.

The bulk stress is the engine of the nonlinearity of the program in that it varies throughout the soil, as obtained experimentally in the laboratory. Typical values for Nigeria base and sub-base materials obtained from “Development of Pavement Evaluation Unit and Rehabilitation Design Procedure for Nigeria under Phase II of the Trunk Road Study” [11], are assumed for the program.

Axisymmetric finite elements procedure, adopted in ‘ABU-PAVE’ (as used in ILLI-PAVE and MICH-PAVE) is used to model structural components that is rationally symmetric about the axis, e.g., solid rings. If these structures are subjected to axisymmeric loads, a two-dimensional analysis of a unit radian of the structure yields the complete stress and strain distribution of the system.

The basic underlying assumptions for the development of ‘ABU-PAVE’ are as follows:

1. A singular circular wheel load is adopted on an axisymetrical rectangular section.

2. Linear material properties are adopted for asphalt concrete and subgrade layers, and non-linear material properties for the unbound base and sub-base layers.

3. Continuity is assumed between the layers, hence interpolation not necessary.

4. The weights of the materials are negligible.

These assumptions are based on the requirement that a basic finite element program is to be developed on MATLAB, on personal computers.

The basic requirements for the generation of the mesh used in this program are how far the vertical and bottom boundaries should be located, the size and shape of the elements, and the distribution of the elements in different regions.

From experience, stresses based on quadrilateral elements will be accurate provided that the length-to-width ratio for the elements does not exceed five to one. Based on these considerations, the following mesh rules were used: the mesh is generated with a full traditional finite element depth of 12960 mm, at which rigid boundary is placed and a width of 10 tire radii (1360 mm), at which a fixed radial boundary is fixed, are adopted for simplicity. The mesh is discredited into 156 rectangular elements of different sizes, with the finest elements closest to the load area. A four node-element is adopted totalling 182 nodes. A standard wheel load of 9000lb (40 kN) was adopted with tire pressure of 80 psi (552 kPa) and radius of 5.35 in (136 mm).

Four layers are defined: the asphalt concrete, unbound base, sub-base and the subgrade, with trial thicknesses of 150 mm, 240 mm, 270 mm and 12300 mm respectively, all divided into tree equal sub-layers each. In the radial direction, the total width of 10 radii is sub-divided into four zones. The 1st zone between 0 and 1 radius is equally divided into four elements; the 2nd zone between 1 radius and 3 radii is equally divided into four elements; the 3rd zone between 3 radii and 6 radii is equally divided into three elements; finally, the 4th zone between 6 radii and 10 radii is equally divided into 2 elements.

The material properties used for the development of ‘ABU-PAVE’ is shown in Table 1. The response outputs (displacements and stresses) generated from the program is presented in the graph of Figure 2 through 5.

Table 1. Material Properties used for the ‘ABU-PAVE’

Layer Type	Thickness (mm)	Modulus, E (MPa)	Bulk Stress,  θ, (MPa)	Poisson’s ratio, υ	K1(MPa)	K2
AC	150	4830		0.35
Base	240			0.38
Subbase	270		210	0.40	50	0.45
Subgrade	12300	193	95	0.45	31	0.53

Comparison of ‘ABU-PAVE’ and NEMPADS

Comparison was made of the generated outputs (stresses, strains and displacements) from ‘ABU-PAVE’ and NEMPADS. This was achieved by adopting uniform material properties for the two programs, and calling for outputs at same critical locations in the pavement section. Vertical components of the output (i.e., vertical stresses, vertical strains and vertical displacements), at the bottom of the AC (just before the AC-base interface) and on top of the subgrade (just after the sub base-subgrade interface), from the programs were chosen for the comparison.

The material properties used for the NEMPADS are presented in Table 2. The outputs generated from the two programs, Table3, obtained at the bottom of AC and on top of subgrade (i.e., 149 mm and 661 mm depth respectively), directly under the load centre.

Table 2. Material Properties used for the NEMPADS

Layer type	Thickness (mm)	Modulus, E (MPa)	Poisson’s Ratio
AC	254	4830	0.35
Base	254	550	0.40
Subbase	254	550	0.40
Subgrade	12192	193	0.45

The comparison of the ‘ABU-PAVE’ against NEMPADS shows a reasonable comparison generally, as indicated in the table 3. The outputs generated from the ‘ABU-PAVE’ are generally lower compared to those of the NEMPADS, and the discrepancies are more pronounce at depth 149 mm (i.e. at the bottom of the AC), especially for the stress values. This is due to the fact that the programs are based on different methodologies (i.e. finite element method and multi-linear elastic method) and that AC was treated as linear elastic instead of visco-elastic material. The strain and displacement values from the two programs compared reasonably at all levels.

Table 3. Comparison of ‘ABU-PAVE’ and NEMPADS

PROGRAM	‘ABU-PAVE’		NEMPADS
Vertical Dept (mm)	149	661	149	661
Stress (kPa)	12.79	17.41	179.95	21.17
Strain (mm)	0.42E-3	2.67E-3	3.28E-3	2.72E-3
Displacement (mm)	0.07E-3	0.03E-3	0.12E-3	0.08E-3

Results and Discussion

It can be seen from figure 2 that the maximum deflection (0.0412 mm) occurs at the pavement surface directly under the applied wheel load centre, and diminishes rapidly away in radial direction in the first zone (since the mesh division is finer in this zone), and gently to uniform value toward the end of the section width. This pattern is also the same for the vertical displacement plotted against depth directly under the applied wheel load centre (figure 3); it can be observed that it exhibits the same maximum value at the pavement surface, diminishes rapidly in the first layer (AC layer), and gently from the base layer to zero value just above the section full depth. This is related to the properties of the materials (i.e., modulus), with AC having the highest modulus and the subgrade lowest. These are compared goodly to the exact solution [5].

The stresses values tend to display uniformity within each layer. This is due to the fact that the layers are not bounded. The radial stress of figure 4 is seen to increase from the pavement surface, attain its maximum value at depth 50mm and decreases rapidly within the AC to the minimum negative value at the AC – base interface; it then increases gently from negative value in the base layer and rapidly in the sub-base layer; and finally reduces gently towards zero in the subgrade layer. It can be inferred that the rate of stress change in each layer is related to the modulus and thickness of the layer in reverse proportion.

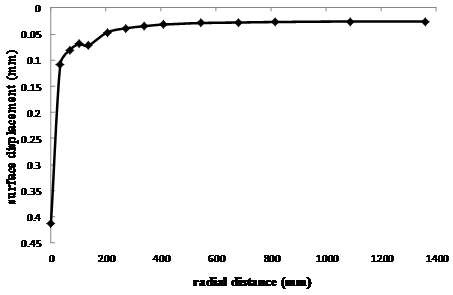
Figure 2. Vertical Displacement along the Surface in Radial Direction

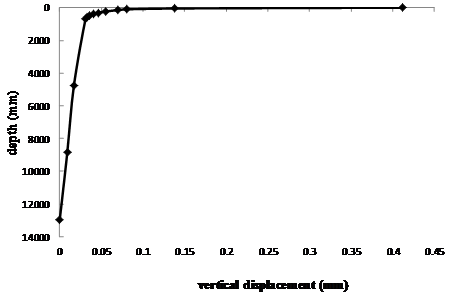
Figure 3. Vertical Displacement in the Vertical Direction under the Load Center

The vertical stress exhibits the same pattern in the AC layer from the pavement surface towards the bottom as the radial stress, but in a reverse direction, as shown in figure 5; it then increases to the highest magnitude of the pavement stress value occurring around the middle of the base layer, which corresponds to one of the critical locations in the pavement section [12, 15], and reduces gently towards zero at the bottom of the subgrade. It can also be observed that maximum value at the base layer for both the radial and vertical stresses, occur at the same location, and correspond to the overall maximum value for the section.

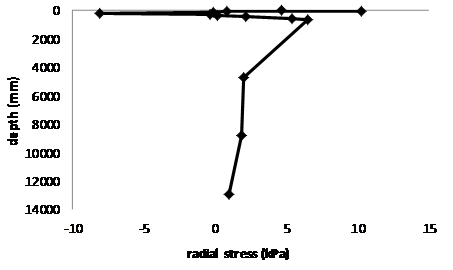
Figure 4. Radial Stress in the Vertical Direction under the Load Center

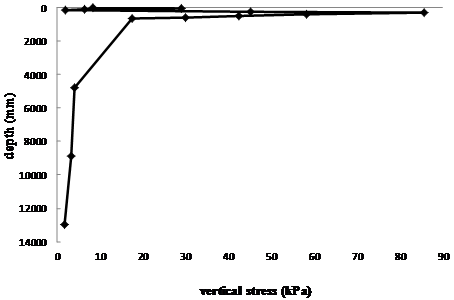
Figure 5. Vertical Stress in the Vertical Direction under the Load Center

At the critical location in the asphalt concrete layer (i.e., at the bottom), the magnitude of the radial stress value, is more than double that of vertical stress value. This conforms to what is obtained in a local pavement program ‘NEMPADS’ [12].

Conclusions

The validity of the developed program – ‘ABU-PAVE’ has been benchmarked against the local available program – NEMPADS, which gave fair comparison. The discrepancies are based on the different methodologies on which the two programs are based. Hence the program can conveniently be used for pavement analysis within the limit stipulated in the assumptions.

It can also be inferred that from the analysis that, for a four layered flexible pavement, the mechanical characterization of AC layer, as a linear elastic medium, is a reasonable approximation of the visco-elastic behavior.

Therefore, the following are recommended for the program:

· The nonlinearity of the program should be strictly based on the model’s stress-dependency, for the base and subbase layers.

· AC and subgrade layers be treated approximately as linear elastic, but AC may be more characterized as visco-elastic.

· Consideration of continuity between the layers of the pavement section.

· The constants of the model (K1 and K2) should be strictly based on the materials properties.

Acknowledgements

Special thanks and appreciations go to the following people who have variously assisted in many ways to make this work a success:

· Professor Yeh, M. S. of Michigan State University, East Lansing.

· Dr. Olowosulu, A.T., of the Department of Civil Engineering, Ahmadu Bello University, Zaria, Kaduna, Nigeria.

References

1. Maina J.W., Denneman E., Debeer M., Introduction of New Road Pavement Response Modeling Software by Means of Benchmarking. Proceedings of the 27^th Southern African Transport Conference (SATC 2008), Document Transformation Technologies CC, Pretoria, South Africa, July 7-11, 2008.

2. Tom V.M., Transportation Engineering I, Transportation Systems Engineering Civil Engineering Department Indian Institute of Technology Bombay Powai, Mumbai 400076, India, 2006.

3. Duncan J.M., Chang C.Y., Nonlinear Analysis of Stress And Strain In Soils, Journal of Soil Mechanics and Foundation, Proceedings of the American Society of Civil Engineers, 1970, p. 1629-1653.

4. Yoder E.J., Witczak M.W., Principles of Pavement Design, 2nd Edition, John Wiley & Sons, New York, 1975.

5. National Cooperative Highway Research Program, (NCHRP), Guide for Mechanistic-Empirical Design of New and Rehabilitated Pavement Structures, Finite Element Procedures for Flexible Pavement Analysis. Transportation Research Board, 2004.

6. Zienkiewicz O.C., Taylor R.L., The Finite Element Method, 4th Edition, McG2raw-Hill, New York, 1989.

7. Bathe K.J., Finite Element Procedures in Engineering Analysis, Prentice-Hall, Private Limited, New Delhi, 1990.

8. Kwon Y.W., Bang H., The Finite Element Analysis Using Matlab, CRC Press, New York. 1st Ed., 1997.

9. Yeh M.S., Nonlinear Finite Element Analysis and Design of Flexible Pavements, Ph.D Dissertation, Michigan State University, East Lansing, 1989.

10. Daba S.G., Comparison of Flexible Pavement Performance using KENLAYER AND HDM-4, Fall Student Conference, Midwest Transportation Consortium, November 25, 2006.

11. Claros G., Carmichael R. F., Harvey J., Development of Pavement Evaluation Unit and Rehabilitation Design Procedure for Overlay Design Method, Overlay Design Manual, Vol. 2., Texas Research and Development Foundation for Nigeria Federal Ministry of Works and Housing, 1986.

12. Olowosulu A.T., A Framework for the Development of Mechanistic-Empirical Pavement Design for Tropical Climate, Nigerian Journal of Civil Engineering, 2005, 5(1).

13. Qin H.Q. and Wang H., MATLAB and C Programming for Trefftz Finite Element Method. 2008; CRC Press, Boca Raton, U. S. A.

14. Kalechman M., Practical MATLAB Basics for Engineers. Taylor & Francis Group, CRC Press, Boca Raton, U. S. A., 2008

15. Garber N.J., Hoel L.A., Traffic and Highway Engineering. 4th Edition. 2009; Cengage Learning 1120 Birchmount Road Toronto ON M1K 5G4 Canada