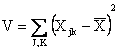Effects of Mould and Pouring Temperatures on the Ultimate Tensile Strength of Aluminium Alloy Sand Castings: An ANOVA Approach

John O. OJI^1*, Buliamin KAREEM², and Nosa IDUSUYI³

¹ Prototype Engineering Development Institute Ilesa, Osun State. Nigeria

² Department of Mechanical Engineering, Federal University of Technology Akure. Nigeria

³Department of Mechanical Engineering, University of Ibadan, Oyo State. Nigeria

E-mails: ojiortega@yahoo.com; karbil2002@yahoo.com; nosaidus@yahoo.com

^* Corresponding author: +234(0)7084089009

Abstract

An analysis of the effects of sand casting process parameters on the ultimate tensile strength of an aluminium alloy sand casting based on the Analysis of variance (ANOVA) technique is proposed in this paper. While other casting parameters were kept constant, the selected parameters were varied and the cast specimen tested to obtain their ultimate tensile strength. Formulation of the varied effects was then made and a statistical tool selected for the analysis. The result of this work shows that the selected technique is an effective tool for analyzing sand casting process. The computed treatment mean square, response mean square and error mean square are 456.35, 57.57, and 59.8 respectively. It is concluded with 90% confidence that the mould temperature is the most significant factor which influences the casting quality in terms of strength under the specified conditions.

Keywords

Pouring Temperature; Mould Temperature; Casting Process Parameters; Ultimate Tensile Strength; Analysis of Variance (ANOVA); Model.

Introduction

The wide ranges of application of aluminium alloys are very obvious. Their desirable characteristics of light weight, excellent resistance to corrosion in the atmosphere and water, strength [1] and high thermal conductivity gives them an edge over other metals in the electrical, aviation, marine, aerospace, construction and automotive industries just to mention but a few [2]. Casting on the other hand is a metal object obtained by allowing molten metal to solidify in a mould [3]. The shape of the object is determined by the shape of the mould cavity.

The applications of statistical tools and concepts that depend heavily on the statistical theory of experimental design in the design and analysis of casting processes have increased over the years [4-6]. Analysis of variance (ANOVA) is a statistical procedure for summarizing a classical linear model (a decomposition of sum of squares into a component for each source of variation in the model) along with an associated test (the F-test) of the hypothesis that any given source of variation in the model is zero [7]. It has been widely used as an effective tool for analyzing highly structured experimental data (in agriculture, multiple treatments applied to different batches of animals or crops; in psychology, multi-factorial experiments manipulating several independent experimental conditions and applied to groups of people; industrial experiments in which multiple factors can be altered at different times and in different locations).

There is no doubt that casting as a process involves so many parameters such as melting temperature of the charge, temperature of the mould, pouring speed, pouring temperature, composition, microstructure, size of casting, runner size, composition of the alloy and solidification time just to mention but a few [8,9, and 10]. The difference in the structure of the casting occurs due to the non-uniform cooling of the molten metal in the mould. This difference resulting in low mechanical properties, if not controlled will affect the performance of the casting while in use [11]. This assertion has led to the evolution of so many processes [12]. Because of the difference in structure of the casting which cannot be eliminated completely in many casting techniques , due to the inability to maintain the law of constant volume par second during the pouring stage, there is therefore the need to investigate the varying effect of some of these parameters on the mechanical properties of similar products. Only two process parameters and one mechanical property are employed in this work. The process parameters are pouring temperature, and mould temperature while the mechanical property is the ultimate tensile strength.

The purpose of the analysis of variance is to investigate the process parameters (factors) that significantly affect the ultimate tensile strength of the castings under the stated conditions.

Material and Method

Preparation of the Charge

At a constant percentage of the iron and silicon, high purity aluminium electrical wires, free from dust and contamination were charged in a graphite crucible kept in an electric resistance furnace. Sodium chloride- potassium chloride (NaCl-KCl) (0.01%) powder was used as a cover for melting the alloy; this helped in minimizing oxidation of aluminium by excluding oxygen and creating a protective atmosphere inside the furnace.

Upon initiation of melting of pure aluminium, the temperature of the furnace was raised to 720°C. The required quantity of silicon (4.6%) and iron (1.5%) was added using Ferro-silicon, and resulting melt thoroughly stirred with progressive melting, the furnace temperature was raised to 780°C and the melt was held at this temperature for ten minutes. It was then skimmed to remove the oxides and impurities.

The molten metal was continuously stirred in order to ensure a near-uniform distribution of alloying elements from settling at the bottom on account of their higher density. For each melting 1.6kg of charge materials were used to produce the alloy. The result of the chemical analysis and the composition of aluminium alloy used are shown in table 1.

Preparations of the Mould and Casting of Specimen 

Foundry sand of known specification was prepared for moulding by adding some quantity of water. The mould boxes (i.e. drag and cope) were produced using wood. One of the boxes was on a board and then a cylindrical pattern was placed on the board. The cylindrical pattern was used because the specimens to be produced are of cylindrical shapes (figure 1). Then the prepared moulding sand was then added to the pattern and rammed, properly. When it was properly rammed, the mould box containing the pattern was turned upside down and the parting sand was applied before placing the other box (i.e. cope). The moulding sand was then added, but before the moulding sand was added, pipes were placed to locate the position of the gate and the riser. The sand was then rammed. When it was properly rammed, the cope was removed and then the pattern was removed. At the sprue the cross-sectional area of the pouring cup was 380mm², and at the cavity the cross-sectional area was 100mm². After this, the assembled mould was placed in a furnace and preheated to temperature of 37°C, 100°C, 150°C, 170°C, and 230°C for holding time of 35 minutes. Again the molten metal was then poured into each mould. After this, the process was repeated with the molten metal poured at pouring temperatures of 700°C, 720°C, 750°C, 770°C and 800°C for holding time of 20 minutes respectively. A total of twenty five samples were prepared.

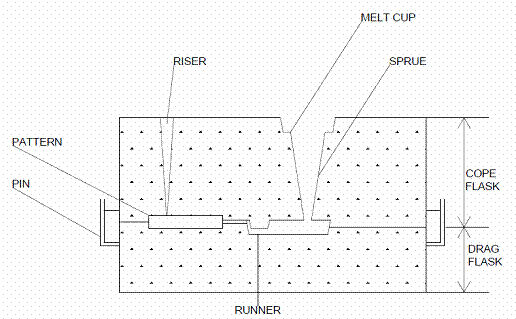
Figure 1. Mould assembly for sand casting

Determination of Ultimate Tensile Test  

The castings were machined to the required shape using the lathe machine as shown in figure 2. The equipment used for the ultimate tensile test is a universal material testing machine, model SSR25 14, digital indicating system. The machine is hydraulically operated. The machined test specimen was then fed into a locking socket which provided grip of the specimen at the base and at the top. With the press loosened to release the extension to allow for easy monitoring on the tensile test piece alongside the socket in which it is fitted, the test piece was held at both end as made to be tensioned slightly and the meter was set to zero with the pump handle in the down position and locked. The pump handle was raised and pressed down so as to apply the load. The load was increased uniformly and the corresponding extension was noted. This process was repeated for other specimens.

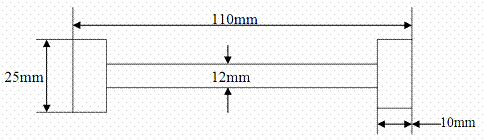
Figure 2. Tensile test specimen

To obtain the ultimate tensile strength the following formula was used [13]:

UTS =Pmax/Ao

(1)

where P_max is the maximum load reading on the machine. A_o  is the original cross sectional area.

Formulation for Two-Factor Experiments  

The formulation adopted for this work is as developed by [14]. Here we have a treatments and b blocks, we construct a model table as shown in table 2, where it is supposed that there is one experimental value corresponding to each treatment and block. For treatment j and block k, we denote this value by X_jk. The mean of the entities in the jth row is denoted by  , where j =1,...,a, while the mean of the entries in the kth column is denoted by ,where k=1,...,b. The overall or grand mean is denoted by  . In symbols:

	(2a)
	(2b)
	(2c)

Variation for Two Factor Experiments  

We define the total variation to be:

(3)

By writing the identity:

(4)

And then squaring and summing over j and k we, can show that:

V=VE+VR+VC

(5)

Where:

	(6)
	(7)
	(8)

V_E is variation due to error. V_R is variation between rows (treatment). V_C is variation between columns (block).

The variation due to error or chance is also known as residual variation or random variation. The following equations are shortcut formulas for computation.

	(9)
	(10)
	(11)
VE=V-VR-VC	(12)

Where T_j is the total of entry in the jth row, T_k is the total of entries in the kth column and T is the total of all entries.

Analysis of Variance for Two Factor Experiment  

The generalization of the mathematical model for one factor experiment is given by [14]:

(13)

Where   and . Here   is the population grand mean,   is that part of  X_jk due to the different treatments (sometimes called treatment effects),   is that part of  X_jk due to the different blocks (sometimes called the block effects) and  is that part of X_jk due to chance  or error. As before, we assume that the  are normally distributed with mean 0 and variance  so that the X_jk are normally distributed with mean  and variance .

It can be proven that the expectations of the variations are given by:

	(14)
	(15)
	(16)
	(17)

There are two null hypotheses that we would want to test:

Ho⁽¹⁾: All treatment (row) means are equal and the parameter (mould temperature) influences strength: that is ,  = 0 and j=1,...,a.

Ho⁽²⁾: All block (column) means are equal the parameter (pouring temperature) also influences strength: that is ,  =0 and k=1,...,b.

From equation (16), without regard to Ho⁽¹⁾ or Ho ⁽²⁾,  a best (unbiased) estimate of   is provided by , that is:

(18)

Also if hypothesis Ho⁽¹⁾ and Ho⁽²)are true, then: 

, ,

(19)

will be unbiased estimates of . If Ho⁽¹⁾ and Ho⁽²⁾ are not true, however, then from equations 14 and 15, respectively, we have:

	(20)
	(21)

To test hypothesis Ho⁽¹⁾, it is natural to consider the statistics.  since it can be seen from equation 19 that is expected to differ significantly from  if the row (treatment) means are significantly different. Similarly, to test hopothesis Ho⁽²⁾ we consider the statistics . Under hypothesis Ho⁽¹⁾, the statistic  has the F distribution with a-1 and (a-1)(b-1) degrees of freedom. Under hypothesis Ho⁽²⁾, the statistics  has the F distribution with b-1 and (a-1)(b-1) degrees of freedom. This enables us to accept or reject Ho⁽¹⁾ and Ho⁽²⁾ at specified significant levels. An analysis of variance table is then constructed as shown in table 4.

Results and Discussion

The chemical composition of the Aluminium alloy casting is presented in Table 1. Table 2 shows the model table employed in the formulation.

Table 1. Chemical composition of aluminium alloy

Element	Al	Fe	Si
Weight Percentage (W %)	93.9%	1.5%	4.6%
Concentration(mgl)	939	15	46

Table 2. Model table

	Block
	1	2	...	b
Treatment 1	X11	X12	...	X1b
Treatment 2	X21	X22	...	X2b
...	...	...	...	...	...
Treatment a	Xa1	Xa2	...	Xab

The results of the effect of mould temperature and pouring temperature on the ultimate tensile strength of the aluminium alloy part are shown in table 3. Results of the ultimate tensile strength were obtained from each test sample. The column means represent the response means while the row means represent the treatment means. The overall grand mean was computed to be 61.5.

Table 3. Effect of mould temperature and pouring temperature on Ultimate Tensile strength

		Pouring temperature (°C)					Means [UTS(N/mm^2)]
		700	720	750	770	800
Mould temperature (°C)	37	76.3	84.7	74.2	69.4	66.4	74.2
	100	66.3	78.4	55.4	75.6	69.5	69.0
	150	62.7	64.0	54.2	54.3	49.5	56.8
	170	41.2	43.4	61.9	65.4	51.1	52.6
	230	55.1	62.9	51.2	54.8	49.5	54.7
Means[UTS(N/mm^2)]		60.3	66.7	59.3	63.9	57.2	61.5

Table 4 shows an Analysis of Variance (ANOVA) table obtained by numerical computation. The mean squares are obtained by dividing the sum of squares of each of the two sources of variation (mould temperature and pouring temperature variance) by the respective degrees of freedom. The F value, known as Fisher variance ratio provides the information on how well the factors describe the statistical variation in the data from its mean. It is calculated by dividing mean square due to model variance to the mean square due to the error. Generally, if the calculated F value is less than the F value obtained from the standard distribution table, the model is a good prediction of the experimental results. From the F-distribution table (statistics table) with 90% confidence, the tabulated value at 4, 16 degree of freedom is given as 2.33. However, the calculated F- values of table 4 are 1.9 and 0.3. According to [5, 14, and 18] we accept the null hypothesis if the calculated F value is less than the tabulated F-Value. Thus, both null hypotheses are accepted and we conclude that the mould temperature and pouring temperature influences the tensile strength of the sand casted part. Pinholes in aluminium castings are caused by the absorbed hydrogen. This can be minimized by pouring the alloy at temperatures just necessary for casting [15]. Hence, upon identification of the optimum pouring temperature, it should be properly applied [16]. Also, since the mould temperature has the least F-value, we conclude that it is the parameter which influences the ultimate tensile strength of the aluminium alloy part the most. This is in tandem with previous work by [17] who adopted the simplex method developed by Dantzig [19] to optimize the effect of sand casting process parameters on the mechanical properties of an aluminium alloy part.

Table 4. Analysis of variance (ANOVA) table

Variation	Degrees of freedom	Mean square	F
Between treatments, VR=1825.4	(a-1)=4
Between blocks, VC=287.85	(b-1)=4
Residual, VE=957	(a-1)(b-1) =16
Total, V=3070.25	(ab-1) =24

Conclusions

Our results indicated that the selected process parameters significantly affect the selected mechanical property. It also shows that the selected tool can be effectively adopted for the analysis of physical processes to explain the relationships between various sand casting parameters. The sequence of the two factors affecting the ultimate tensile strength is the mould temperature and pouring temperature respectively. At 90% level of significance, the mould temperature is the most significant factor which influences the casting quality in terms of strength. The results of this work can be applied in foundry shops where it is evident that the number of defective castings produced is on the high side. Work is in progress to adopt the ANOVA technique to more than two sand casting process parameters (pouring speed and runner size) and to include other mechanical properties such as impact strength and hardness.

References

1. Allen D.K., Metallurgy Theory and Practice. American Technical Society, Chicago (ASM), 1979, p. 238-239.

2. Karl B. Metal Casting, Quickest and Least Expensive Route to a Near Shape Product. Reference Book for MY4130. Materials Science and Engineering Department, Michigan Technical University, USA., 2005, pp. 150-165.

3. Sanders R.E, Technology Innovation on Aluminium Casting. Microsoft Corporation U.S.A. 2001, p. 37-42.

4. Johnston R.E., Design of experiments: Taguchi in the foundry. AFS Trans., 1989, 82, p. 415-418.

5. Kumar P., Gaindhar J.L., Off-line quality control for V-process castings. Qual. Reliab. Eng. Int., 1995, 11. p. 175-181.

6. Barua P.B., Kumar P., Gaindhar J.L, Surface roughness optimization of V process castings through Taguchi's method. AFS Trans., 1997, 45. p. 763-768.

7. Gelman A., Analysis of variance: why it is more important than ever (with discussion). Annals of Statistics, 2005, 33, p. 1-53.

8. Abu El-Aini H., Mohamed K. Hassan, Y. Mohammed. Effect of mould types and cooling rate on mechanical properties of Al alloy 6061 within ceramic additives. The 2nd International Conference on Energy Engineering ICEE-2, December 27-29, 2010 - Aswan, Egypt, 2010.

9. Timelli G., Bonollo F., The influence of Cr content on the microstructure and mechanical properties of AlSi₉Cu₃(Fe) die casting alloys. Mat. Sci. Eng. A, 2010, 528, p. 273-282.

10. Lee C.D., Effects of microporosity on tensile properties of A356 aluminium alloy. Mater. Sci. Eng. A, 2007, 464. p. 249-254.

11. Novikov I., Theory of heat treatment of metals. Mir publishers, Moscow, 1986, pp. 407.

12. Jatau J.S., Datau S.G., The influence of thermo-mechanical properties of lead alloy. Nigeria Journal of Engineering, ABU Zaria, 2002, 10, p. 1-6.

13. Donald R.A. The Science and Engineering Materials. Second edition PWs-KENT Publishing Company, 1989.

14. Murray R.S., Larry J.S., Theory and Problem of Statistics. Fourth Edition. Schaum's Outline Series. McGRAW-HILL publishers, New York, 2007, p. 403-412.

15. ASME, Pouring Temperature Ranges for Metals and Alloys, Publication of American Society of Mechanical Engineering, Vol. III, Chicago U.S.A., 1996.

16. Mohammad B.N., Akpan P.P., Behaviour of Aluminium Alloy Castings under Different Pouring Temperatures and Speeds. LEJPT, 2007, 11, p. 71-80.

17. Oji J.O., Pamtoks S.H., Optimizing the effect of sand casting process parameters on the mechanical properties of an aluminium alloy part. Unpublished HND Project Submitted to the Department of Mechanical Engineering, The Federal Polytechnic Bauchi, 2007.

18. Lipson C., Sheth N.J., Statistical Design and Analysis of Engineering Experiments. McGraw-Hill, Inc. USA., 1973, p. 194-205.

19. Philips D.T., Ravindran A., Solberg J.J., Operations research: principles and practice, Second Edition. John Wiley and Sons Inc. New York. U.S.A., 1987.