Consequences and Limitations of Conventional Computers and their Solutions through Quantum Computers

Nilesh BARDE¹, Deepak THAKUR², Pranav BARDAPURKAR³ and Sanjaykumar DALVI^3*

¹ Badrinarayan Barwale Mahavidyalaya, Jalna, India

² School of Physical Sciences, Swami Ramanand Teerth Marathwada University, Nanded, India

³ S. N. Arts, D.J. Malpani Commerce & B. N. Sarda Science College, Sangamner-422605, India

E-mail: sanjaykumardalvi@gmail.com

^* Corresponding author: Phone: +91-9850014466

Abstract

Quantum computer is the current topic of research in the field of computational science, which uses principles of quantum mechanics. Quantum computers will be much more powerful than the classical computer due to its enormous computational speed. Recent developments in quantum computers which are based on the laws of quantum mechanics, shows different ways of performing efficient calculations along with the various results which are not possible on the classical computers in an efficient period of time. One of the most striking results that have obtained on the quantum computers is the prime factorization of the large integer in a polynomial time. The idea of involvement of the quantum mechanics for the computational purpose is outlined briefly in the present work that reflects the importance and advantages of the next generation of the 21st century classical computers, named as quantum computers, in terms of the cost as well as time period required for the computation purpose. Present paper presents a quantum computer simulator for executing the limitations of classical  computer with respect to time & the number of digits of a composite integer used for calculating its prime factors.

Keywords

Quantum Computer; Qubits, Superposition; Quantum Parallelism.

Introduction

Today in the computing world, innovations are leading to powerful miniaturized integrated circuits. In accordance with Moore’s law, chip capacity is doubled after every 18 months. Making chips smaller, as we approach ~10 nm size, weird things happen with the electrons reveal quantum nature and the principles of classical physics are no more obeyed at such scales. Thus, it is necessary either to develop new semiconductor chips, which could bypass the quantum nature or embrace the quantum nature. Currently, the choice made by scientists is to embrace the quantum nature i.e. to employ the principles of quantum mechanics for building novel computers called quantum computers [1-3].

The conventional computers and the information processing that every one of us is familiar, obey the well-understood principles of classical physics. A classical computer basically manipulates and interprets binary bits into a useful computational result. A bit represents a fundamental unit of information, represented by 0 or 1. In chips, voltage levels indicate 0 or 1. The classical computers though have become compact and fast, cannot solve problems such as factoring of a large integer. The large digit prime numbers are used to send messages in coded form. Currently the single transistor on a chip is turned on or off by using around hundreds of electrons. In future it is proposed that the transistors will be controlled by a single electron and is said to be the single electron transistor (SET) in which the laws of classical physics is unable to describe the physical systems but the principles of quantum mechanics are used to explain the physical phenomenon [2].

Further, using the concept of quantum parallelism (discussed later), it is proposed that the power of quantum computers will be able to solve efficiently the most difficult problems in the theory of computational science such as factorization of large integers, database search problems, discrete logarithms which are difficult to solve by using the present computers in the specific period of time [3]. In the theory of quantum computation, the physical quantities are represented in terms of two-state quantum systems viz; polarization state of photon, spin directions of electrons or atomic nucleus in the magnetic field. However, in developing such systems lot of challenges are presented.

The power of the quantum computer promises to solve efficiently the most difficult problems in the theory of computational science such as factorization of large integers, database search problems, discrete logarithms which are difficult to solve by using the present classical computers in the speculated period of time [4-5]. The voltage levels in the current microprocessors to indicate the physical quantities are known to everyone. But in the developing theory of quantum computation, the physical quantities are represented in terms of two-state quantum systems viz; polarization state of photon, spin directions of electrons or atomic nucleus in the magnetic field although people are facing lot of challenges in developing such systems. Following is a brief discussion of the quantum computers with its building blocks and the development stages.

The present work was aimed to develop the algorithms for factorization of an integer. In the present study, the algorithm was developed to factorize a large integer on the conventional computer. To show the variation in the speed of the factorization of different numbers of various digits, the different RAM’s were used. The program, which was developed, is in C++ language.

Material and Method

Basic Building Blocks

The few concepts, which play an important role in building the quantum computational theory, are the qubits, superposition, quantum parallelism, and entanglement.

a. Qubits:  In the present classical computers the electric current flowing through the conducting wires is in the two basic states i.e. when there is no current flowing then it is said to be logical ‘0’ or else when there is flow of current then it is represented as logical ‘1’. These two states form a bit of information. But in the quantum computation the information is recorded in terms of the two electronic states of an atom and the each bit of information carried by quantum computers is called as ‘quantum bit’ or ‘qubit’ that represents 0, 1 or any value in between them at the same time. This bi-stable state quantum system can be physically realized by the photons, spin-1/2 particles, polarization of electrons, etc which is represented in a two dimensional complex Hilbert space [6].

b. Superposition: The electronic states of an atom for the ground and excited levels are defined as   and   respectively which is in terms of the Dirac notation and is most suitable for the quantum computation. But according to the laws of quantum mechanics the electronic state of an atom is the superposition of the two basic states and is represented by the wave function ψ as:

(1)

Where, α and β are the two complex vectors which satisfies the condition:

(2)

In case of classical computers the two bits can be represented as 00, 01, 10 and 11. But the quantum two-bit in contrast can represent any of those numbers simultaneously. Consequently if the number of qubits increases the number of   superposition will exponentially increases which results in calculating the complicated numbers speedily which the current computer technology is not able to compute [7-8].

c. Quantum parallelism: The principle of superposition is used to develop the concept of parallelism to create the new quantum microprocessors. In the macroscopic world the atoms are traveling in many different directions and in different routes. The basic idea is that the computer should use these atoms to perform the multiple calculations simultaneously. In other words the quantum computers can perform the various calculations at the same time. By using the concept of parallelism the quantum computer can do the factorization of large number, which the classical computer is unable to process. For example, the factorization of a 500-digit number can be done by the supercomputers in billions of years, which the quantum computer can do in a year. Similarly for searching information from the large unsorted database the concept of quantum parallelism can be used [9].

d. Entanglement: The quantum entanglement is the process in which the atoms are entangled in such a way that without interference of the outer world the one atom spins in one direction, the rest will be spin in some direction which can be mathematically related to each other. By using the superposition and entanglement, the complex algorithms can be created which are used to solve the billions of calculations. The information can be processed from the sender to receiver securely with the help of the entanglement effect. Any attempt to eavesdropper will be detected and the message is totally disturbed. In the current scenario, the main barrier in front of the researchers is to manipulate the atoms using quantum physics to achieve entanglement [10-11].

Challenges in Building Quantum Computers

For the computation purpose, the qubits should couple together, measure there states and then should be kept relatively free from interactions that induce noise and de coherence. The some of the electrical systems that can produce by modern lithography such as nano scaled quantum dots and tunnel junctions are used for constructing the qubits. People have got the success to develop some of the physically realizable systems such as ultra small Josephson junctions, cold ion traps, nuclear spin quantum computation, harmonic oscillator quantum computer and NMR quantum computation [9, 12]. But, the main problem which remains common to all the realization systems is that of the de coherence i.e. the quantum information is spread outside the quantum computer and lost in the environment which spoils the computation. To overcome the above problem, physicists are using some principles and the conditions in choosing the system in which the qubits should be in a reliable physical form and can be prepared with the required set of initial states. The some of the conditions before designing the physical systems are:

a) The qubits should be given some physical representation in which they can show their quantum properties and can be evolved to a desired state;

b) The qubits should be prepared in a specified set of initial states i.e. the input state is to be designed perfectly;

c) The input states will be different for different physical systems.

To remove the decoherence, it is supposed that there should be a measurement of time for which the system remains coherent and also the time required to perform the computation. The qubit implementation is the major problem during the computation process. The qubits can be implemented in different ways such as spinning of the particles, polarization of photons and the ground and excited states of the atoms. While selecting the physical representation of the qubit, the decoherence time is to be considered which also affects the speed of the computer i.e. if the qubit interacts strongly with the external world; the speed of the computer is more.

For building the quantum computers, there are great challenges before the scientists and engineers. It is well known that the quantum computation runs with the atomic scale systems in the enormous size of the Hilbert space. The computation involves building a trajectory from a standard initial state to a complex final state. In order to have environmental error free coupling, the basic problem is to maintain this trajectory. The perturbation comes from coupling to the external noise and one of the promising ways identified to isolate the quantum systems is the ion trap technique [11].

Another problem is about the quantum factoring of a number, which requires many thousands of coherent 2-qubit operations to factor numbers that would not be easy to factorize by the classical methods.  Rapid   progress in laser cooling and thermal isolation suggests that it will indeed be feasible to maintain such isolation long enough for processing a ten qubits of quantum information. The main obstruction comes in making these devices is the noise which takes place a fundamental barrier for the information processing. There is a threshold theorem for quantum computation, which provides the level of noise in a quantum computer, which can be reduced below a certain value.

Importance of Prime Factorization

In most of the public-key cryptosystems, the large random prime numbers of fixed bit length as well as the larger integers whose prime factors is to be calculated are required. In this section the special emphasis is made to discuss the importance of long integers and their prime factors in the secure communication channels considering the example of Alice and Bob who use the symmetric cryptosystem in which they exchange the secret keys before they communicate on a private channel. The problem of key exchange is very difficult if there are many people who are encrypting messages on the Internet. In general, if there are n number of users in a network and any two of them exchanges a key, then n(n-1)/2  secret key exchanges are necessary and these keys are to be stored securely which is very much impossible to organize. A key centre is the possibility for organizing the key exchange. The every user exchanges a secret key with this key centre. Now, the centre is knowing all secret keys - decrypts the messages using Alice’s key - encrypts its with the Bob’s key and finally sends it to Bob. Thus, the number of key exchanges for n users is reduced to n. Now, the key centre knows all secret messages and it stores all n number of keys securely.

In case of a public key system, the decryption key is to be kept secret and is called a private key. Computing private keys from their public keys is infeasible and is the crucial property of the public-key cryptosystems. In this case, if Bob wants to send a message to Alice, he obtains Alice’s public key from the key directory. Then he uses this public key to encrypt the message and sends it to Alice. Alice is then able to decrypt the message with her private key viz; in the directory the public key of Alice may be a long integer i.e. 54628291982624638121025032510. In the public key systems there is no key exchange between the users. The encryption keys are listed in the directories. The people can read those directories but are protected from the unauthorized writing [6].

The public-key cryptosystem is said to be secure if the problem of computing the secret key from publicly available information is intractable. There are some algorithms in quantum computers such as Shor’s algorithm which can solve the problems very efficiently and can also breaks all public-key cryptosystems which are used today. The public-key cryptosystems is said to be secure as long as a few well-defined computational problems such as factoring of large integers are intractable. RSA cryptosystem is the one whose security is closely related to the difficulty of finding the factorization of the large composite positive integer, which is a product of two large primes. The structure of the RSA cryptosystem is discussed in detail in the previous chapter. The only point of discussion for the RSA cryptosystem in this section is to show the importance of the selection of the two initial large prime numbers p and q whose product is the composite number. In this case, the secret key d can be calculated from the encryption exponent e if the prime factors p and q of n are known. Thus, the eavesdropper can find out the Bob’s secret key d if he is able to calculate the prime factors of the large composite integer n. This shows that if anybody can find out the efficient factoring algorithm of large integers then the RSA cryptosystem is said to be insecure. After 1980’s, people have found out many algorithms, which can factor large integers in polynomial time. The Shor’s algorithm is the one, which can factor a large integer on quantum computer. But, still the research is in the developing stage to build the large quantum computers [6]. Until then the RSA cryptosystem is said to be the secure one. This shows the importance of the factorization of a large composite integer for the secure communication purpose.

The quantum computation is an exciting frontier of the computer science that may provide a computational power to the human beings. At present, people are come to know some of the hints of the power of quantum computers and have got success to grapple few practical problems that are involved in the construction of the large scaled quantum computers [7]. Some of the problems from the quantum computation and information theory such as factorization of large integers, Grover’s database search problems, quantum counting, etc. are formulated for quantum programs and are thought to be the quantum programming problems. Unfortunately quantum computers are counter-intuitive and is difficult to program. But, fortunately we can adapt the existing programming technologies such as C++, which can contribute in understanding the quantum computing problems [5]. The C++ language is used to formulate the program for the factorization of large integers and also the prime number generator, which is the core of the thesis and is discussed in detail including the flow charts, algorithms and the different syntax used [13-16].

Results and Discussion

In all, the programs are developed which are successfully compiled on the classical computer that includes finding the factors of long integer up to the 9-digits. The programs are developed in C++ language in which the results of the programs includes the prime factors of different long integers with the time period required for calculation & the limitations of the number of digits involved which can be factorized on the conventional computers.

The results of the program for integer factorization are shown in the figure 1 below that shows the time period required for the execution of the prime factors for different composite integers with the different number of digits on the classical computers in presence of the different RAM memory chips in it i.e. of 128 MB to 2 GB.

Figure 1 shows that as we increase the speed of the classical computers by using the different RAM’s and executes the same program for prime factorization then we see that the time period required for the calculation of the factors goes on decreasing even if the number of digits of the composite integer increases.

The composite integers, which are greater than or equal to ten digits fails to execute the factors by using the classical computers even if its speed is kept at their maximum limit.

This shows the limitations of the classical computers as it can accept the string of the digits up to 232 in the binary form.

The numbers shown in the above example goes beyond that limit due to which the computer does not give any response or it may go into the hang condition.

To execute the factors of the large numbers whose string goes above the limitations of a single computer, the more than one computers are to be used whose processors are connected to each other in such a way that the total speed and the   frequency of the assembly is definitely greater than that of the single computer.

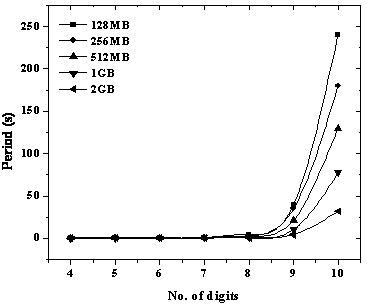
Figure 1. Trend lines for time period required for splitting composite numbers

The environment used for computing the prime factors is the assembled single PC with the frequency of 3.16 GHz along with the variation of RAM from 128 MB to 2 GB. The maximum digit, which can be factorized with the above configuration, is the 9-digit number, which can be factorized with few minutes of time. This can be observed in the fig.1, which shows the trend lines for the time period required for executing the composite number into the prime factors. To factor the larger number the more number of PC’s are required with the higher configuration to reduce the time period of factorization.

Thus, as the number of digits of the composite number whose factors are to be calculated is increased, the number of processors in the assembly should be increased to meet the speed of the calculation. Here, the importance of the quantum computers came into picture as it has an advantage over the classical computers in terms of the cost as well as time period. If the quantum computers are successfully build then in case of the mentioned problem more particularly in calculating the prime factors of a large composite numbers, the only single quantum computer will be sufficient to factor even a thousand digit number, also within a few hours only for which the classical computers requires the time period which may be equivalent to the age of our Universe.

Acknowledgements

Authors are thankful to Dr. P.M. Kokne, Badrinarayan Barwale Mahavidyalaya, Jalna and S. P. Sansthas’ Sangamner College, Sangamner.

References

1. Nielsen M.A., Chuang I.L., Quantum Computation and Quantum Information, Cambridge University Press, Cambridge, 2000.

2. Bennett C.H., Bernstein E., Brassard G., Vaizirani U., Strengths and weaknesses of quantum computing, SIAM J. Comput., 1997, 26, 1510-1523.

3. Shor P.W., Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer, SIAM J. Comput., 1997, 26, 1484-1509.

4. Datta A., Shaji A., Caves C. M.; Quantum discord and the power of one qubit, Phys. Rev. Lett., 2008, 100, 050502.

5. Ferraro A., Aolita L., Cavalcanti D., Cucchietti F.M., Acín, A.; Almost all quantum states have nonclassical correlations, Phys. Rev. A, 2010, 81, 052318.

6. Liberty J., Keogh J., C++ An Introduction  to  Programming, Prentice-Hall of India, New Delhi, 1997.

7. Aaronson S., Watrous J., Closed timelike curves make quantum and classical computing equivalent. Proceedings of the Royal Society A - Mathematical, Physical and Engineering Sciences, 2009, 465, 631-647.

8. Kaye P., Mosca M., Quantum networks for generating arbitrary quantum states, Proceedings of the International Conference on Quantum Information, OSA CD-ROM (Optical Society of America, Washington, D.C., 2002) quant-ph/0407102

9. Poulin D., Classicality of quantum information processing, Phys. Rev. A, 2002, 65, 42319.

10. Cummins H., Jones C., Furze A., Soffe N., Mosca M., Peach J., Jones J., Approximate Quantum Cloning with Nuclear Magnetic Resonance,  Physical Review Letters, 2002, 88, 187901.

11. Mair A., Vaziri A., Weihs G., Zeilinger A., Entanglement of Orbital Angular Momentum States of Photons, Nature, 2001, 412, 313-316.

12. Clark R.J., Lin T., Brown K.R., Chuang I.L., A two- dimensional lattice ion trap for quantum simulation, Journal of Applied Physics, 2008, 105, 013114.

13. Zhang J., Long G., Deng Z., Liu W., Lu Z., Nuclear Magnetic Resonance Implementation of a Quantum Clock Synchronization Algorithm, Phys. Rev. A, 2004, 70.

14. Yashwant Kanetkar, Let us C, BPB Publications, New Delhi - India, 2010.

15. Kong D.X., Wang A.M; Quantum-state transfer on spin-chain channels with random imperfections; The European Physical Journal D - Atomic, Molecular, Optical and Plasma Physics, 2009, 55(1), p. 211-221.

16. Mohamed El-fiky, Satoshi Ono, Shigeru Nakayama; Study on discrete adiabatic quantum computation in 3-SAT problems; Artificial Life and Robotics, 2011, 16(1), p. 107-111.