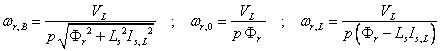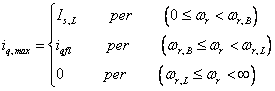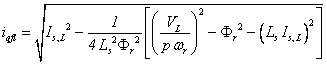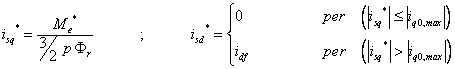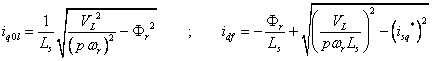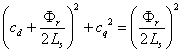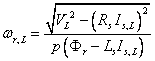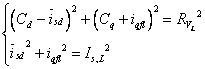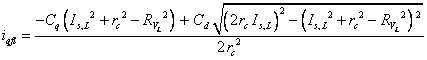A novel Control Algorithm Expressions Set for not Negligible Resistive Parameters PM Brushless AC Motors

Renato RIZZO^1*, Andrea DEL PIZZO¹, and Ivan SPINA¹

¹ Department of Electrical Engineering - University of Naples Federico II

Via Claudio 21, Naples, Italy

E-mails: renato.rizzo@unina.it; andrea.delpizzo@unina.it; ivanspina@gmail.com

^* Corresponding author: Phone: +39 081 7683231

Abstract

This paper deals with Permanent Magnet Brushless Motors. In particular is proposed a new set of control algorithm expressions that is realized taking into account resistive parameters of the motor, differently from simplified models of this type of motors where these parameters are usually neglected. The control is set up and an analysis of the performance is reported in the paper, where the validation of the new expressions is done with reference to a motor prototype particularly compact because is foreseen for application on tram propulsion drives. The results are evidenced in the last part of the paper.

Keywords

Permanent magnets; Brushless motor.

Introduction

Permanent Magnet brushless motor drives (PMSM) are widely demanded in many and various application such as generation by renewable sources like wind [1,2], and especially in industrial and traction applications [3-6], thanks to their compactness and good dynamic features. As all motors utilized in electric drives or any other complex system, nowadays also smart energy distribution systems [7-9], it is necessary to feed them by power electronic converter and set up proper control of the whole drive according to the specific requested operation and performance [10-13].

In order to improve their performance, reliability and availability, many control algorithms have been proposed in literature, starting from the value of the electrical parameters in the Park’s reference system.

These algorithms are mainly based on the hypothesis to neglect motor resistive parameters. This hypothesis is not acceptable in case of very compact motors, i.e. light traction motors, in these cases is preferred to have a lower efficiency and dissipate the loss energy adopting a more efficient liquid cooling system. Such simplified control algorithms can introduce unacceptable errors that can produce damages to the machine or reduce their lifetime [14].

The influence of resistive drops on machines voltage depends in particular on the load and speed. A quick method to evaluate the negligibility of resistances could be the evaluation of the influence of resistive drop on the rated voltage. Acceptable values are 1-2%, for higher values is better to redefine the operative limits and control trajectories.

In the paper is proposed a control algorithm which is realized taking into account the resistive parameters of the motor, the control is validated by a numerical analysis with reference to a motor prototype for tram propulsion application.

                        Preliminary Definition and Traditional PMSM Expressions

In order to see how the several PMSM mathematical expression get modified ones the resistive parameters are introduced, it is convenient to recall them. The rotor reference system mathematical model is reported in (1) together with the torque expression.

(1)

The traditional control of the motor is based on the model (1) and the reference current components i_sd^*, i_sq^* must ensure the satisfaction of the two main limits of operation (2) and (3) regarding respectively the maximum current (I_s,L) and the maximum voltage (V_L)

	(2)
	(3)

in particular (3) is written from the first of (1) in steady-state operation, separating the d,q components and using the approximation of negligible resistive parameters. In Park’s reference system the (3) represents the equation of a circle centered in (-Φ_r/L_s,0) and with radius (V_L/pω_rL_s). In fig.1-a the (2) is depicted together with (3) for three specific value of speed called ‘characteristic speeds’ of the motor.

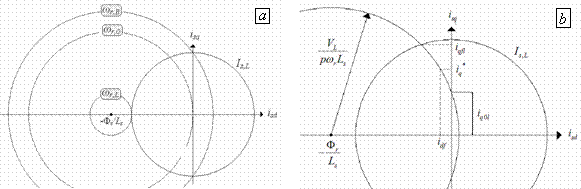
Figure 1. a) Characteristic PMSM speeds for simplified expressions b)Main current limits for simplified expression

The expression of the characteristic speeds ω_r,B, ω_r,0 and ω_r,L is:

(4)

The maximum i_q current component is indicated with i_q,max and is:

(5)

with:

(6)

if is known the desired torque T_e^* at the fixed speed ω_r, the reference current component i_sd^*, i_sq^* are expressed by:

(7)

with:

	(8)
	(9)

A geometrical representation of i_q0l, i_df is reported in fig.1-b.

                        Limit Expressions Modified by Resistive Parameters Introduction

Since the resistive parameters are not always negligible, they should be taken into account when defining the control algorithm trajectories. In particular the approximation used in the maximum voltage (3) has to be removed and a complete expression has to be considered:

(10)

in comparison with (3), (10) still represents the equation of a circle, but with different center and radius, the radius R_VL and the coordinates of the center c_d, c_q are:

	(11)
	(12)

The sign of inequality in (10) represents the inner area of the circle. If R_s=0, as it can be noticed, relations (10-12) yield the expressions traditionally used to define the voltage boundary of a PMSM. Since the resistance is a physical parameter, it cannot be equal to zero, this leads to the following considerations:

1. At null speed, the maximum current which satisfies the voltage limit is not infinitive, but equal to V_L/R_s (the order of magnitude of this value is quite high, typical of short circuit current values);

2. At fixed speed, the value of current for not overcoming the voltage limit becomes equal to (11), which can be seen as the ratio between the voltage V_L and an impedance with R_s as real part and pw_rL_s as imaginary part;

3. The coordinates c_d, c_q are speed dependent.

From the (12) it is possible to write:

(13)

where pw_r can be calculated from the second of (12):

(14)

To obtain the final relation between the coordinates c_d and c_q, (14) is substituted into (13), this yields:

(15)

then it is possible to understand how the center of the circle (10) moves when speed increases. In fact, (15) is another equation of a circle centered in the point (−F_r/2L_s) and with radius F_r/2L. When speed is zero, c_d = c_q =0, and the center of the circle (10) is situated in the origin of axis; with the approximation (3) this center was always placed in (−F_r/2L_s, 0), independently from the speed. By increasing the speed, c_d and c_q become different from zero and both negative, if w_r is assumed positive (for positive w_r eq.15 describes a semi-circle). Thus, with the increase of the speed the center of the circle moves on the semi-circle (15), as depicted in fig.2.

In fig.2 is represented (15) with the semi-circle in dashed line, the arrow (clockwise) is coherent with the positive increasing of w_r, the point (−F_r/2L_s,0) has been reported for w_r→∞; only for w_r→∞ the center of the approximated expression (3) coincides with the one of (10). The circle in continuous line indicates the maximum current I_s,_L.

If the motor parameters are known, for any value of w_r the coordinates c_d, c_q are univocally defined, together with the radius R_VL, this allows to individuate the working area on the d,q domain; an example is given in Fig.3.

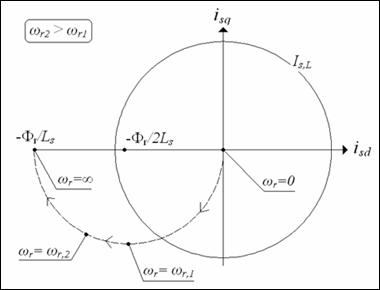
Figure 2. Voltage limit centre displacement on Park’s reference system and current limit

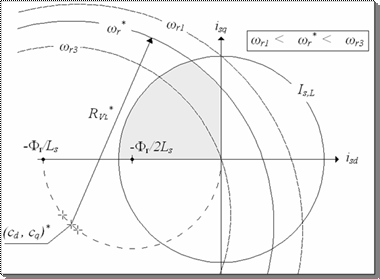
Figure 3. Working area on Park’s reference system when using complete expressions

The working area is colored in grey in fig.3 for a fixed value of the speed w_r^*. On the same figure it is also possible to see how the working area gets enlarged or contracted for respectively higher and lower value of speed.

With respect to the approximated expression (3), (10) yields a reduced working area on the first quadrant of d,q domain. This happens because the circle (10) has a shorter radius and its center is moved in the negative direction of q-axis.

Same considerations can be done also with reference to the PMSM mathematical model (1): the addition of the resistive voltage drop (R_s I_s) makes the voltage V_s reaching its own limit for lower values of current I_s, at fixed speed w_r, and/or for lower value of w_r, fixing the current I_s.

The modification of the working area in d,q axis reference is reflected on the T_e −w_r domain as well, changing the definition of characteristic speeds and the values of maximum d,q current components which satisfy the limit of the voltage. This influences also the control algorithm, modifying the reference trajectories.

New Control Reference Trajectories

All the characteristic speeds above defined, considering the new maximum voltage expression (10), have to be re-calculated. Also their representation on d,q domain appears different than the one of fig.1, and it is proposed in fig.4.

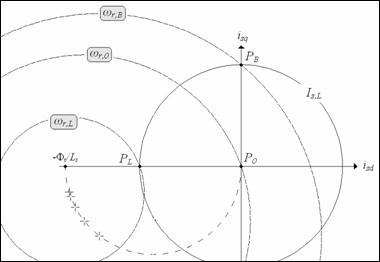
Figure 4. Characteristic PMSM speeds when using complete expressions

The characteristic speed w_r,_B has been calculated starting from the maximum voltage expression (3) and imposing i_d=0, i_q=I_s,L. The base speed w_r,_B has now to be re-defined as:

((16)

Applying the same procedure, the limit speed changes in:

(17)

Differently from w_r,_B and w_r,_L the characteristic speed w_r,₀ does not change with the introduction of resistive parameters, because it is calculated imposing zero i_d, i_q current components in the maximum voltage expression; w_r,₀ remains defined by (4).

By adding the resistive parameters in the maximum voltage expression, also the maximum current changes, in particular the component i_q0l, i_qfl, have to be re-calculated, while their composition remain the one of (8) and (5) in the different ranges of speed. For sake of simplicity the following positions are adopted:

(18)

In fig.5 (10) and (2) are depicted in d,q domain for a fixed value or w_r >w_r,_B, and i_q0l is the ordinate of the point A.

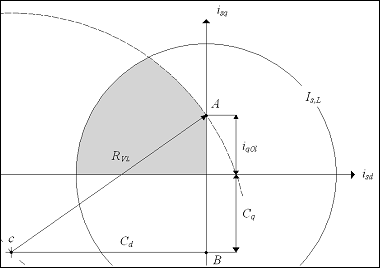
Figure 5. Q-axis current limit for applying ‘max(T/I) strategy’ when using complete expressions

By applying Pythagoras theorem, i_q0l is calculated:

(19)

The same can be done for the quantity i_qfl (ordinate of point A in fig.6).

From fig.6 it is simple to verify that:

(20)

Which gives the i_qfl expression:

(21)

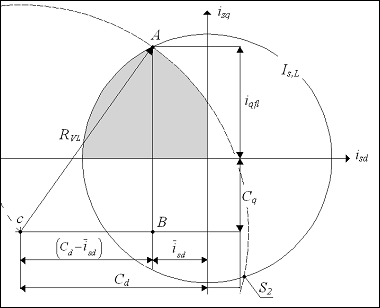
Figure 6. Q-axis current limit when using complete expressions

In flux weakening region, the d-axis current component i_df  expressed by (9) has now to be re-defined. In fig.7 the reference current component i_sq^* is supposed to be known and the speed w_r assigned higher than w_r,_B. The component i_df is necessary to assure that the voltage keep within the maximum value V_L.

The current i_df can be easily calculated by means of geometrical consideration and is:

(22)

Ones assigned the reference torque T_e^* at fixed speed w_r, the reference current components is formally defined, but the quantities w_r,_B, w_r,_L, i_q0l, i_qfl, i_df have to be calculated respectively as in (16), (17), (19), (21) and (22); while w_r,₀ remains defined by (4).

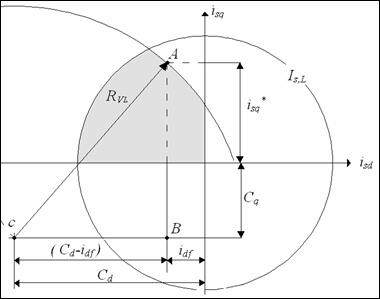
Figure 7. Flux weakening d-current when using complete expressions

Numerical Analysis

A numerical analysis is carried out with reference to a traction advanced prototype motor whose parameters are reported in table1.

Table 1. PMSM motor parameters

Rated values
Power	Pn	67.5 kW
Electromagnetic torque	Te,n	2014 Nm
Speed	ωr,n	33.51 rad/sec
Current (rms)	Is,n	120 A
Phase voltage (rms)	Vf,n	286 V
Limit values
Electromagnetic torque	Te,L	2910 Nm
Current (maximum)	Is,L	170 A
Phase voltage (maximum)	VL	286 V
Stator phase resistance	Rs	332 mΩ
Stator self inductance	Ls	5.40 mH
Permanent magnets flux-linkage	Фr	0.998 Wb

This water-cooled motor is intended to replace the actual induction motors on tram application and, in order to eliminate the speed reducer and lowering the floor, it has been designed with the specification of high compactness [15]. This makes the resistance a not negligible parameter and the resistive voltage at rated current turns to be about 14% of V_f,n.

With reference to the motor of tab.1, in fig.8-a the working area on the T_e - w_r domain is delimited by two different curves. The outer curve refers to i_q,max with i_qfl calculated as in (6) based on the approximation (3). The inner curve, instead, refers to the complete expression (21) of i_qfl.

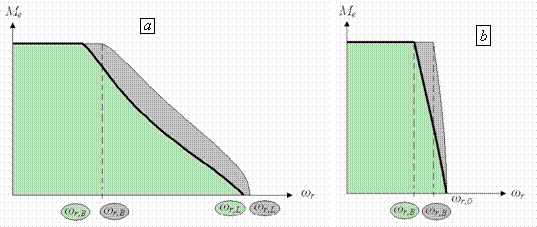
Figure 8. T_e-ω_r domain for approximated and complete expression:

a)when using ‘flux weakening strategy’ b) when using ‘maximum torque/current strategy’

The portion of the domain where the ‘maximum torque/current strategy’ is possible is represented in fig.8-b; as before the outer curve refers to the approximated i_q0l (9), while the inner curve refers to the complete expression (19) of i_q0l. As it can be noticed, the resistive parameters contract the working area in order to ensure that the voltage keeps within its limit. If vice versa the control algorithm was not based on the complete expression of the limits, it would force the motor to work on the darker portion of fig.8 overcoming the limit voltage. On the other hand, the simplified expressions are easier to be implemented and require a lower computational burden from the control system. A different solution to ensure the voltage within proper limits is using the approximated expression but choosing a value for V_L lower than the rated voltage V_R. In fig.9 the working area – divided in the part of ‘maximum torque/current strategy’ and ‘flux weakening strategy’’ – is reported for two different set of equations: the red line refers to the complete expression and with V_L equal to V_R; the black line refers to the approximated expression with V_L nearly equal to 94% of V_R.

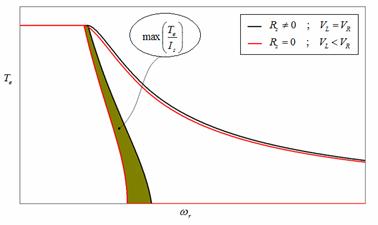
Figure 9. T_e-ω_r domain for complete expression with the right value of V_L and for approximated expression with a lower value of V_L

The use of approximated expression with lower V_L drags the outer line of the calculated domain within the real limit, but produces a restriction of the ‘maximum torque/current strategy’ domain, as it can be seen in fig.9. This reduces the motor performances and increase the loss of power.

Conclusions

A novel control algorithm expressions set for not negligible resistive parameters PM Brushless AC motors has been proposed in the paper. This algorithm is based on a new set of control algorithm expressions that is realized taking into account resistive parameters of the motor, differently from simplified models of this type of motors where these parameters are usually neglected. The control has been presented and explained including a critical analysis of the performance, the validation of the new expressions is done with reference to a motor prototype particularly compact because is foreseen for application on tram propulsion drives. The results complete the paper evidencing the effectiveness of the novel algorithm proposed for light trains application.

References

1. Piegari L., Rizzo R., Tricoli P., High Efficiency Wind Generators with Variable Speed Dual-Excited Synchronous Machines, Proceedings of International Conference on Clean Electrical Power ICCEP 2007, Capri (Italy), 2007, pp. 795-800.

2. Pillay P., Krishnan R., Modelling, Simulation, and Analysis of Permanent-Magnet Motor Drives, Part I: The Permanent-Magnet Synchronous Motor Drive, IEEE Transactions on Industry Applications, 1989, 25(2), p. 265-273.

3. Benchaib A., Alacoque J.C., Poullain S., Thomas J.L., Discrete-time field-oriented control for SM-PMSM under asynchronous and synchronous PWM operations, Proceedings of 11th International Power Electronics and Motion Control Conference (EPE-PEMC), 2004.

4. Belin S., Scrooby M., Masselus J., Jobard T., Courtine S., A PMSM based control for traction applications, Proc. of European Conference on Power Electronics and Applications (EPE), 2003.

5. Bae B.H., Sul S.K., Kwon J.H., Shin J.S., Implementation of sensorless vector control for super high speed PMSM of turbocompressor”, IEEE Transactions on Industry Applications, 2003, 39(3), p. 811-818.

6. Ahmadi D., Nasiri A., A Novel Digital Control Method of PMSM for Automotive Applications, Proc. Vehicle Power and Propulsion Conference VPPC, 2007, p. 180-184.

7. Brando G., Dannier A., Del Pizzo A., Rizzo R., A High Performance Control Technique of Power Electronic Transformers in Medium Voltage Grid-Connected PV Plants, Proc. of International Conference on Electrical Machines ICEM 2010, Roma (Italy), Sept., 2010, p. 1-6.

8. Brando G., Dannier A., Rizzo R., Power Electronic Transformer application to Grid-connected Photovoltaic Systems, Proceedings of International Conference on Clean Electrical Power 2009, Capri (Italy), June, 2009, pp. 685-690.

9. Andreotti A., Del Pizzo A., Rizzo R., Tricoli P., An efficient architecture of a PV plant for ancillary service supplying, Proceedings of International Symposium on Power Electronics Electrical Drives Automation and Motion (SPEEDAM 2010), 2010, Pisa (Italy), June, 2010, pp. 678-682.

10. Simanek J., Novak J., Dolecek R., Cerny O., Control Algorithms for Permanent Magnet Synchronous Traction Motor,. Proc. International Conference EUROCON 2007; Sept., 2007, pp. 1839-1844.

11. Aguirre M., Calleja C., Lopez-de-Heredia A., Poza J., Aranburu A., Nieva T., FOC and DTC comparison in PMSM for railway traction application, Proceedings of 14th European Power Electronics and Applications (EPE 2011), 2011, pp. 1-10.

12. Brando G., Dannier A., Del Pizzo A., Rizzo R., Quick identification technique of fault conditions in cascaded H-Bridge multilevel converters, Procedings of International Aegean Conference on Electrical Machines and Power Electronics ACEMP 2007, Bodrum (Turkey), Sept., 2007, pp. 491-497.

13. Rizzo R., Tricoli P., Power Flow Control Strategy for Electric Vehicles with Renewable Energy Sources, Proceedings of Power and Energy Conference PECon 2006, Malaysia, Nov., 2006, pp. 34-39.

14. Fodorean D., N'diaye A., Bouquain D., Miraoui A., Characterization and control of a permanent magnet synchronous motor used in vehicle application, International Conference on Automation Quality and Testing Robotics (AQTR), 2010, 3, p.1-6.

15. Peroutka Z., Zeman K., Krus F., Kosta F., Control of permanent magnet synchronous machine wheel drive for low-floor tram, Proceedings of 13th European Conference on Power Electronics and Applications (EPE), 2009, 1-9.