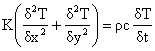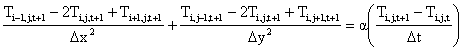Numerical Simulation of Steady State Conduction Heat Transfer during the Solidification of Aluminum Casting in Green Sand Mould
Victor ANJO*
Department of Mechanical Engineering, Federal University of Technology, Minna, Niger State, Nigeria
E-mail: victoranjo2008@live.com
* Corresponding author: Phone: +2348057846076
Abstract
The solidification of molten metal during the casting process involves heat transfer from the molten metal to the mould, then to the atmosphere. The mechanical properties and grain size of metals are determined by the heat transfer process during solidification. The aim of this study is to numerically stimulate the steady conduction heat transfer during the solidification of aluminum in green sand mould using finite difference analysis 2D. The properties of materials used are industrial AI 50/60 AFS green sand mould, pure aluminum and MATLAB 7.0.1. for the numerical simulation. The method includes; the finite difference analysis of the heat conduction equation in steady (Laplace’s) and transient states and using MATLAB to numerically stimulate the thermal flow and cooling curve. The results obtained are: the steady state thermal flow in 2D and transient state cooling curve of casting. The results obtain were consider relevant in the control of the grain size and mechanical properties of the casting.
Keywords
Numerical Simulation; Conduction heat transfer; Aluminum and green sand mould.
Introduction
Casting is a manufacturing process by which a liquid material is usually poured into a mould, which contains a hollow cavity of the desired shape, and then allowed to solidify. The solidified part is also known as a casting, which is ejected or broken out of the mould to complete the process. Casting materials are usually metals or various cold setting materials that cure after mixing two or more components together; examples are: concrete, clay and plaster [5]. The solidification of materials depends on the cooling rate of the materials which is governed by heat flow in the mould and alloy composition [12]. Solidification rate also affects the structure and properties of the materials. One of the critical elements that have to be considered for producing a high quality in sand casting product is the Cooling rate and gating design [10]. The cooling rate depends on the rate of heat transfer from the mould cavity to the atmosphere through the mould. This work will dwell on the conduction heat transfer from the mould cavity to the atmosphere, during the casting of aluminum. Solidification takes place through nucleation and growth of the solid phase under favourable thermal conditions. Homogeneous nucleation, which involves the formation and survival of solid nuclei whose radii are larger or equal to the critical radius, it depends of the free energy, volume and surface. Nucleation takes place below the melting temperature in equilibrium, characterizing the occurrence of thermal super-cooling. [2] and [6]
When the temperature is reduced uniformly throughout the liquid, extensive random nucleation occurs throughout the liquid. However, the practical conditions of heat flow promote the formation of temperature gradients in the liquid, which induce initial nucleation on the mould’s walls, with grain growth taking place toward the centre of the cast part. Nucleated grains with the most favourable orientation grow preferentially, advancing toward the bulk of the casting by progressive deposition of atoms in the solid-liquid interphase. Lateral growth is restricted by competitive growth, resulting in the formation of column-like and elongated grains growing in the direction of the thermal flow [11].
The objective of this paper was to analysis the conduction heat transfer in a sand mould using finite difference method. This study investigates the steady state and transient cooling conduction heat transfer during the solidification of an Aluminum casting in green sand mould.
Material and Method
Mould Employed
Generally speaking, the type of mould employed strongly influences the quality of the cast part in terms of dimensions, shape, surface finish and internal quality; hence, it is indispensable the appropriate selection and control of the materials of which the mould is made, showed by [2]. The mould employed for this study is a green sand mould with industrial sand, AI 50/60 AFS.
Modes of Heat Transfer
There are basically three modes of heat transfer namely: conduction, convection and radiation. Conduction which focuses on the transfer of heat energy through the direct impact of molecules, convection which results from the energy transferred through the motion of a fluid and radiation which focuses on the transmission of energy through electromagnetic waves [9]. The simulations performed by accounting the dependence of the melting point on the interface concentration, show that the moment of the destabilization coincides with the appearance of significant fluctuations in the liquid solutal profile [10].
The governing differential equation for conduction heat transfer transient nonlinear state in 2D is given by:
|
|
(1) |
For steady state, equation (1) becomes:
|
|
(2) |
Laplace equation the solution to equation (2) is:
|
T(x, y, 0) = f(x, y) |
(3) |
Where K = Thermal conductivity in W/mK, ρ = Density in Kg/m3, T = Temperature in Kelvin(K) and t = Time in seconds.
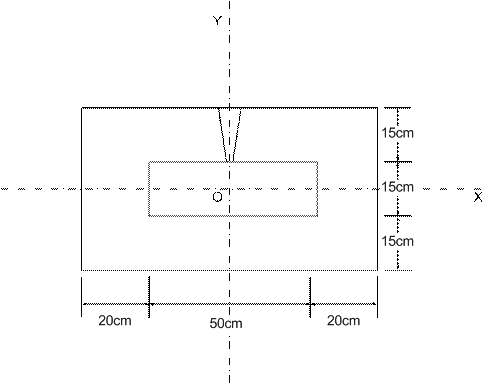
Figure 1. Schematics of Mould
From figure 1 above, heat is transferred from the mould cavity and gating through the mould sand mix to the atmosphere.
Finite Difference Analysis of Conduction Heat Transfer
In this study, only Cartesian square meshes will be used. The increments in x, and y directions are denoted by ∆xi, and ∆yj, respectively. The smaller these increments are the better is in agreement with the true temperature distribution.
The equation (1) above can be written in its finite different form as:
|
|
(4) |
where:
|
|
(5) |
|
|
(6) |
Equation (6) denotes the finite difference form of the Laplace equation (2), equation (4) is for transient state while equation (6) is for steady state [8].
Since heat transfer is in two dimensions, length A = 90cm and Height B = 45cm of Mould are shown in figure (1) above.
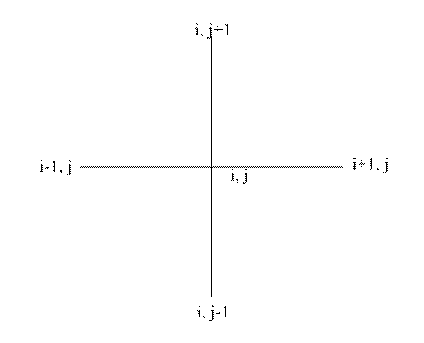
Figure 2. Nodes Layout
Boundary conditions:
Initial condition, t = 0, Tm = Temperature of molten metal or alloy in mould cavity and Tai = Initial atmospheric temperature (Foundry shop temperature).
At x = y = 0,
|
|
(7) |
Where q = quantity of heat transfer in Joules (J), hf = latent heat of fusion in (KJ/Kg) and Tambient = Ambient temperature in Kelvin (K)
Final condition, t = t, Ts = temperature of mould cavity after solidification of metal or alloy and Tfa = Final atmospheric temperature (after solidification of molten metal)
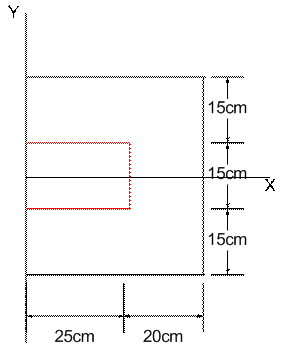
Figure 3. Half of the mould
Methodology of the Numerical Simulation
MATLAB 7.0.1. R14 service pack 1 software program was used to simulate the temperature distribution during the solidification of pure aluminum in green-sand moulds, with the aid of a Pentium ® Dual core CPU 2.2GHz with 64 bits windows vista operating system computer. The following procedures were use for the simulations:
1. Half of the mould (right side) was considered since both the right and left sides of the mould are Symmetry.
2. Both the transient and steady heat conduction states were considered.
3. The materials used were in pure state, the table 1: below shows the properties of the materials.
4. Initial boundary conditions; atmosphere/ambient temperature = 301 K, temperature of molten aluminum inside the mould cavity = 973 K, length of the mould along the horizontal axis = 45cm and height of the mould along the vertical axis = 45cm.
5. The final step consists in solving the problem of heat transfer of the mould – cast metal system, using Equations (4), (6) and controlled by the convergence condition. The time of processing for the simulation was of 7200 seconds. The result of the heat transfer is shown in 2-D, as well as the cooling curve in the cast metal.
Table 1. Physical properties of pure Aluminum and industrial sand, AI 50/60 AFS, according to [4] and [2]
|
Material |
Specific heat (KJ/Kg. K) |
Density (Kg/m3) |
Thermal Conductivity (W/m. K) |
|
Aluminum |
0.8963 |
Liquid = 2375 Solid = 2700 |
237 |
|
Industrial sand, AI 50/60 AFS |
1172.3 |
1494.71 |
0.52 |
|
Latent heat of fusion of aluminum hf = 10.71KJ/mol |
|||
Results and Discussion
The numerical simulation of the temperature distribution in the steady state heat conduction can be seen in figure 4 using MATLAB 7.0.1. We can see that the temperature is maximum at the centre O of the mould (T = 973 K, x = 0 and y = 22.5cm) and as we move along the mould cavity through the x and y axes, the temperature gradually drops until we get to the ambient temperature at T = 310 K, x = 45cm and y = 0 or 45cm (outer surface of the mould).
The phenomenon of convection and radiation that occurs between the mould and the environment was not consider in this study. In this case, the properties of the mould materials were considered as constant, while that of aluminum varied according to state of matter. Figure 4, shows the steady state temperature distribution from the center of the casting where the temperature is 973 K to the atmosphere where temperature is 301 K.
Figure 5 shows the cooling curve of the casting from a temperature of 973 K to 310 K in 2 hours (7200 seconds). The simulation of the gradual cooling of the casting and cooling of the mould aids a foundry man to control proper grain growth which in turn provides quality casting with better mechanical properties.
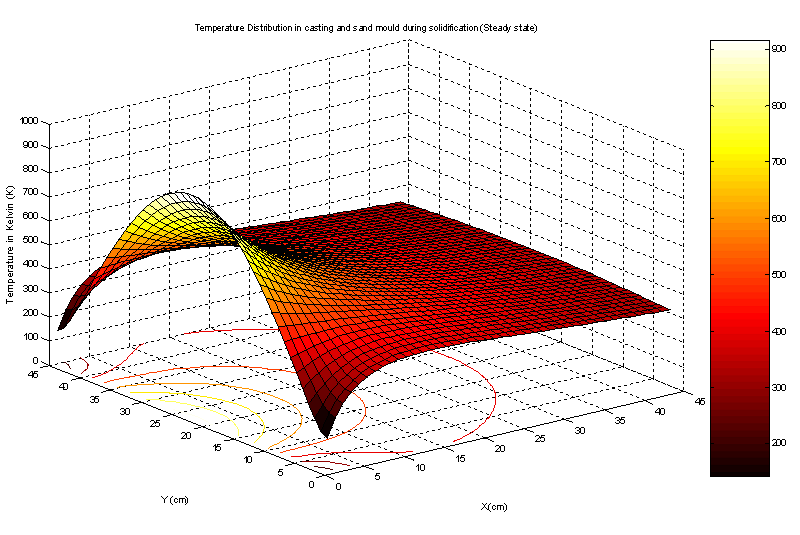
Figure 4. Temperature distribution in casting and green sand mould during solidification (steady state)

Figure 5. Cooling curve in Aluminum casting
Conclusion
This study show the numeric simulation by the finite difference analysis of the temperature distribution and cooling process of aluminum in green sand mould, during 2 hours of solidification. Results were obtained in 2D, the results are: transient cooling curve of castings and the steady state thermal flow through the casting and mould.
References
1. Attar E.H., Babaei R.P., Asgari K., Davami P., Modelling of air pressure effects in casting moulds, Journal of Modelling and Simulation in Materials Science and Engineering, 2005, 13, p. 903-917.
2. Campbell J, Casting, Butterworth-Heinemann, Oxford, 1991.
3. Stelian C., Numerical analysis of constitutional super cooling during directional solidification of alloys, Journal of Material Science, DOI 10.1007/s10853-011-6193-1, 2011.
4. David P., Massone J., Boeri R., Sikora J, Gating system design to cast thin wall ductile iron plates, International Journal of Cast Metals Research, 2006, 19(2), p. 98-109.
5. Degarmo E.P., Black J.T, Kohser R.A, Materials and Processes in Manufacturing, 9th Edition, Wiley Inc, USA, 2003.
6. Flemings M.C., Solidification processing, McGraw-Hill, New York, 1974.
7. Hertzberg R.W., Deformation and fracture mechanics of engineering materials, John Wiley & Sons, New York, 1996.
8. Kreyszig E., Advanced Engineering Mathematics, Part E Numerical Analysis and software, 9th edition, Wiley & Sons Inc, USA, 2006.
9. Kutz M., Mechanical Engineering Handbook, second edition, John Willey and Son Inc, USA, 1998.
10. Masoumi A., Effect of Gating Design on Mould Filling, American Foundry Society, USA, 2007.
11. Pariona M.M., Mossi A.C., Numerical Simulation of Heat Transfer During the Solidification of Pure Iron in Sand and Mullite Molds, Journal of the Brazilian Society of Mechanical Science and Engineering, 2005, XXVII(4), p. 399-406.
12. Shaha S.K., Haque M.M., Simulation of Heat Flow in Computational Method and Its Verification on the Structure and Property of Gray Cast Iron, American Journal of Applied Sciences, 2010, 7(6), p. 795-799.
13. Symbolic Math Toolbox™ 5 User’s Guide, Revised for MATLAB, Version 5.2 (Release 2009a), The MathWorks, Inc, 2009.
14. Young-Chan K., Chang-Seog K., Jae-Ik C., Chang-Yeol J., Se-Weon C., Sung-Kil H., Die Casting Mold Design of the Thin-walled Aluminum Case by Computational Solidification Simulation, Journal of Material Science Technology, 2008, 24(3), p. 383-388.