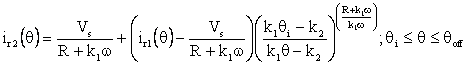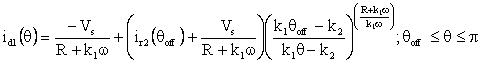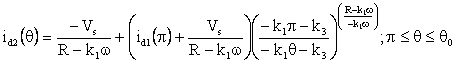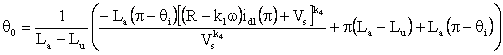Control Methods of the Switched Reluctance Motor in Electric Vehicle During Acceleration

Fathy El Sayed ABDEL-KADER¹, Mohsen Z. ELSHERIF², Naser M.B. ABDEL-RAHIM², and Mohamed M. FATHY²*

¹ Faculty of Engineering, Menofia University, G. A. Nasser St., Shibin El kom, Egypt

²Faculty of Engineering, Benha University, 108, Shoubra St., Cairo, Egypt

E-mails: fatkader2@yahoo.com; elsherif.mohsen@yahoo.com; nabdelrahim@gmail.com; eng_mohfathysaad@yahoo.com

^* Corresponding author: Phone: 01226283560; Fax: +(202) 26708584)

Abstract

In this paper, the equations describing the performance of the electric vehicle are derived. Performance characteristics for each part in the vehicle system are obtained when the vehicle is accelerated under voltage, turn on and turn off angle control. A comparison between the different methods of control is established.

Keywords

Switched Reluctance Rotor (SRM); Electric vehicle; Acceleration mode.

Introduction

The internal combustion engine (ICE) vehicle at the present is a major source of urban pollution. According to figures released by the U.S. Environmental Protection Agency (EPA), conventional ICE vehicles currently contribute 40%–50% of ozone (nonmethane organic gases NMOG), 80%–90% of carbon monoxide (CO), and 50%–60% of air toxins (nitrogen oxides NOx) found in urban areas. Beside air pollution, the other main objection regarding ICE automobiles is their extremely low efficiency use of fossil fuel. Hence, the problem associated with ICE automobiles is threefold: environmental, economic, as well as political. These concerns have forced governments all over the world to consider alternative vehicle concepts [1–3].

Electric vehicles (EV) offer the most promising solutions to reduce vehicular emissions. EV constitute the only commonly known group of automobiles that qualified as zero emission vehicles (ZEVs). These vehicles use electric motors for propulsion and batteries as electrical energy storage devices [1, 2]. Figure 1 shows The Drivetrain of the electric vehicle

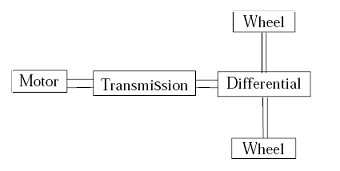
Figure 1. The EV Drivetrain

Switched reluctance motor (SRM) are perhaps the simplest of electrical machines. They consist of a stator with excitation windings and a magnetic rotor with saliency. Rotor conductors are not required because torque is produced by the tendency of the rotor to align with the stator produced flux wave in such a fashion as to maximize the stator flux linkages that result from a given applied stator current.

Due to simple and rugged motor construction, low weight, potentially low production cost, undemanding cooling, excellent torque–speed characteristics, high torque density, high operating efficiency, and inherent fault tolerance, switched reluctance motor (SRM) drives are emerging as an attractive solution for electric vehicle (EV) applications [4–13]. Traction performances of EVs depend on the performances of SRM drives. Hence, the excellent motoring operation of SRMs is important for EVs with high performances.

The aim of this research was studying the different methods of control of the SRM in the electric vehicle to choose the most appropriate one.

Material and Method

Performance Equations of the EV with Acceleration Mode

To investigate the EV performance at acceleration it will be assumed that the vehicle is accelerated under certain values of the motor terminal voltage, turn on and turn off angle. The voltage equation of each phase winding can be expressed as:

v = i R + (dλ (i,θ)/ dt)

(1)

Neglecting the saturation of the magnetic circuit, the phase flux linkage can be expressed by:

λ (i,θ) = L(θ) i

(2)

By substitution from equation (2) into equation (1), the motor phase voltage can be written as:

v = i R + L(θ)(di/dt)+i(dL(θ)/dt)

(3)

Also equation (3) can be rewritten as:

v = i R + L(θ)(di/dθ)(dθ/dt)+i(dL(θ)/dθ)(dθ/dt)

(4)

At steady state, the motor speed can be determined as a function of the rotor position by:

ω =dθ/dt

(5)

where ω, θ are the motor speed in (elec. rad/s) and the rotor position in (elec. rad) respectively. Substituting from equation (5) into equation (4), the motor phase voltage can be expressed as:

v = i R + L(θ) ω(di/dθ)+iω(dL(θ)/dθ)

(6)

where the three terms of the above equation represents the resistive drop, the self and rotational EMF respectively. Finally after rearranging equation (6), the motor phase voltage can be rewritten as:

v = ( R + ω(dL(θ)/dθ)i+ωL(θ)(di/dθ)

(7)

From Figure 2 the motor phase inductance can be represented as a function of the rotor position as:

L(θ) = Lu;0 ≤ θ ≤ θi L(θ) = k1 θ – k2;θi ≤ θ ≤ π L(θ) = – k1 θ – k3; π ≤ θ ≤ (2π– θi) L(θ) = Lu; (2π– θi) ≤ θ ≤ 2π

(8)

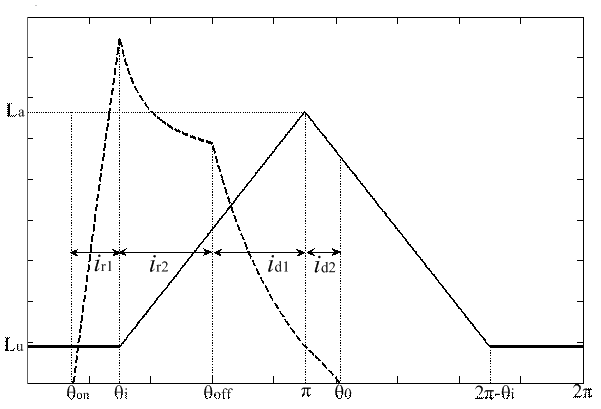
Figure 2. Motor phase inductance and current against the rotor position

The constants k₁, k₂, k₃ and θ_i are equal with:

k₁=(L_a-L_u)/(π-θ_i)

K₂=(L_aθ_i-L_uπ)/(π-θ_i)

K₃=(-π(L_a-Lu)-(L_a(π-θ_i)/(π-θ_i)

θ_i=π-N_rβ_r

According to the motor phase voltage there are two modes of operation of the SRM. At the first mode of operation the motor phase voltage is connected to the DC supply voltage V_s thus the motor phase current will be increases. At the second mode the applied voltage on the motor phase is the negative value of the DC supply voltage, thus the motor phase current will be decays to zero value. 

Substituting from equation (8) into equation (7) taking into account the specified modes of operation, the motor phase current can be obtained for each rotor position range, included in Figure 2, as:

(9)

Where these equations are derived to represent the following range for the turn on and turn off angle: θ_on < θ_i and θ_off < π. Also θ₀ is the angle at which the motor phase current equal zero after decaying. This angle can be determined from equation (9) by putting (i_d2=0 and θ=θ₀):

(10)

where the constant k₄ is:

k₄=(-k₁ω)/(R-k₁ω)

Therefore, the motor torque is expressed by:

Te=(i^2/2)(dL(θ)/dθ)

(11)

The motor speed can be expressed in terms of the vehicle speed as:

ωm=m(Vveh/rwh)

(12)

where m is the gear ratio of the mechanical coupling between the motor and the axle of the vehicle wheels. Assuming lossless transmission, the developed torque at the shaft of the wheel axle can be determined by:

Td_wh=mTe

(13)

The corresponding tractive force will, thus, be:

FTR=Td_wh/rwh

(14)

The tractive force developed at the shaft of the wheel axle during acceleration can be expressed by:

FTR=kmMveh(dVveh/dt)+FRL

(15)

where the road load force is [1,6,10-13]:

FRL=C0Mveh g+Mveh g sin(β)+0.5ρCDAfVveh^2

(16)

Thus, the load torque at the shaft of the wheel axle can be expressed by:

Twh= FRL rwh + Tb

(17)

Also, the load torque at the shaft of the motor axle can be expressed by:

TL=Twh/m

(18)

Therefore from equation (15), the acceleration of the vehicle can be expressed by [4]:

(dVveh/dt)=(FTR-FRL)/kmMveh

(19)

Also using the motor torque and speed, the motor output power can be expressed by:

Pmo = Te  ωm

(20)

The motor power losses can be determined by:

PLoss = nph Iph^2 R

(21)

where I_ph is the average value of the motor phase current. The motor excessive energy can be determined from:

Eexc = nph (Iph- Ir)^2 R dt

(22)

where I_r, dt are the rated value of the motor phase current and the time step.

Principle of Numerical Solution

Starting from zero vehicle speed at certain values of the motor turn on, turn off angle and terminal voltage, from equation (12) the motor speed would be equal to zero. From equation (9) and (10), the motor phase current can be determined. When the motor phase current exceed the rated value the motor voltage, turn on or turn off angle is controlled to make the motor phase current within permissible value. 

Then using the phase current into equation (11) the motor developed torque, T_e, can be obtained. Also from equation (20) and (21) the motor output power, P_mo, and the motor power losses, P_Loss, can be determined respectively. Multiplying the predetermined motor phase current by the motor terminal voltage, the motor input power, P_m in, can also be obtained. Thus using the motor input and output power the motor efficiency, η_m, can be obtained. Using equation (22) the motor excessive energy, E_exc, can be determined and then from equation (6) the motor rotational and self EMF can be calculated. From equation (14) and (16), the tractive and road load forces can be determined at this vehicle speed respectively.

Using these values of the tractive and road load force into equation (19), the next vehicle speed can be obtained by integrating this equation numerically over an appropriate time step. For the second and following time steps of numerical solution, the corresponding motor speed is obtained from equation (12). Then equation (11) is used to obtain its motor developed torque and the corresponding tractive force is obtained from equation (14). This process continues until the vehicle reaches steady-state speed.

Results and Discussion

The approach presented in (3), was applied using 4th order Runge-Kutta numerical method of integration. Using the data of the switched reluctance motor and vehicle given in Appendix, the performance characteristics of the vehicle are obtained when the vehicle is accelerated to 160 Km/h under three method of control. At the first method of control the vehicle is accelerated under a controlled terminal voltage, to maintain the phase current within the rated condition, while the turn on and turn off angle are maintained at the optimum values (0°, 30° respectively). At the second method of control the vehicle is accelerated under controlled turn on angle, to maintain the phase current within the rated condition, while the motor terminal voltage and turn off angle are maintained constant at the optimum values (280 v, 30° respectively). At the third method of control the vehicle is accelerated under controlled turn off angle, to maintain the phase current within the rated condition, while the motor terminal voltage and turn on angle are maintained constant at the optimum values (280 v, 0° respectively).

Figure 3 shows the variation of the vehicle speed throughout the acceleration period in the three cases when the vehicle is accelerated under voltage control (at θ_on = 0° and θ_off=30°), turn on angle control (where V_s = 280 v and θ_off = 30°) and when the vehicle is accelerated under the turn off angle control (where V_s = 280 v and θ_on = 0°). From this figure it is clear that in the three cases the vehicle will reach to the same final steady-state speed (160 Km/h) and the acceleration time, for the case at which the turn on angle is controlled, will be smaller than that for the other cases also the acceleration time, for the case of voltage control, will be the largest.

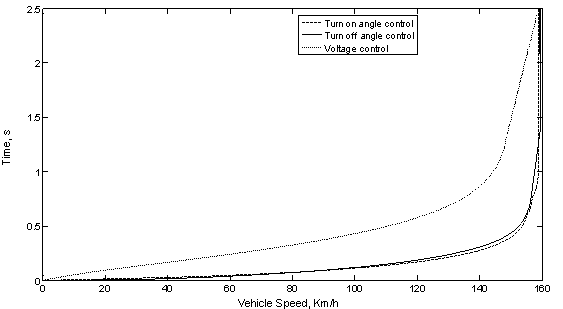
Figure 3. Time versus vehicle speed at vehicle acceleration under the different control methods.

Also figures 4, 5 and 6 shows the motor terminal voltage, turn on and turn off angle, respectively, when the vehicle is accelerated under the different method of control illustrated previously.

From Figure 4 it is clear that the motor terminal voltage will be varies from 50 v to 280 v, during acceleration under the voltage control but in the other cases the motor terminal voltage is maintained constant at the optimum value (280 v).

Also from Figure 5 it is noticed that the motor turn on angle started from 17.5° to 0°, during acceleration under the turn on angle control while in the other cases the turn on angle will be maintained constant at the optimum value (0°).

From Figure 6 it is clear that the motor turn off angle will be varies from 14° to 30°, during acceleration under the turn off angle control but in the other cases the turn off angle is maintained constant at the optimum value (30°).

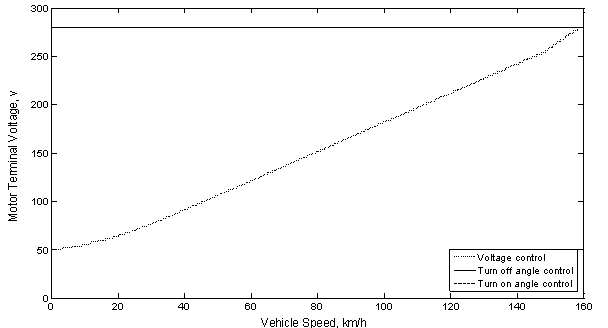
Figure 4. Motor terminal voltage versus vehicle speed at acceleration under the different control methods.

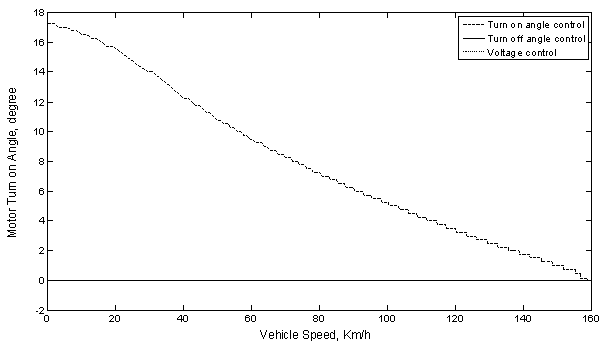
Figure 5. Motor turn on angle versus vehicle speed at acceleration under the different control methods.

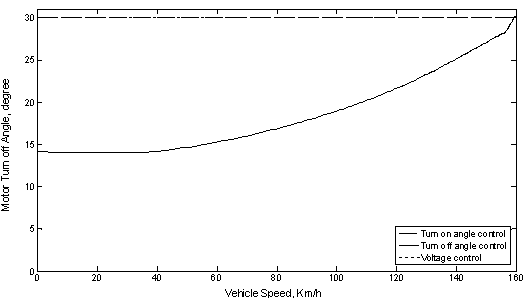
Figure 6. Motor turn off angle versus vehicle speed at acceleration under the different control methods.

Using the values of the vehicle speed, which are obtained from equation (9-10), the motor phase current can be plotted against vehicle speed, for the different cases of control illustrated in figure 7. It is noticed that the motor phase current is maintained constant within the rated condition during the acceleration period under the different cases of control.

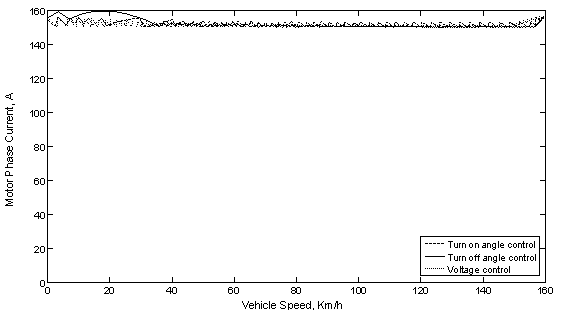
Figure 7. Motor phase current versus vehicle speed at acceleration under the different control methods.

Using the values of the vehicle speed, which are obtained previously, into equation (9) and (10) then substituting into equation (11), the characteristics of the motor developed torque, T_e, can be obtained for the different methods of control illustrated earlier. Also from equation (18), the motor load torque, T_L, can be estimated. Then the motor developed torque and load torque are drawn versus the vehicle speed, during acceleration until steady-state conditions are reached, as shown in Figure 8. From this figure it is clear that the motor developed torque, for the case of voltage control, is increase slightly as the vehicle accelerates but for the other cases of control the motor developed torque started high and then decrease as the vehicle speed increase. At certain vehicle speed the motor developed torque, at the voltage control method, have lower values than that of the other methods of control during the acceleration period. Also the motor developed torque, at the turn off angle control method, have the highest value especially at the lower vehicle speed (< 40 Km/h) and the motor developed torque, at the turn on angle control method, have the highest value at vehicle speed higher than 40 Km/h, finally the load torque increases as the vehicle speed increases up to steady-state speed at which the curves of the developed and load torques are intersected.

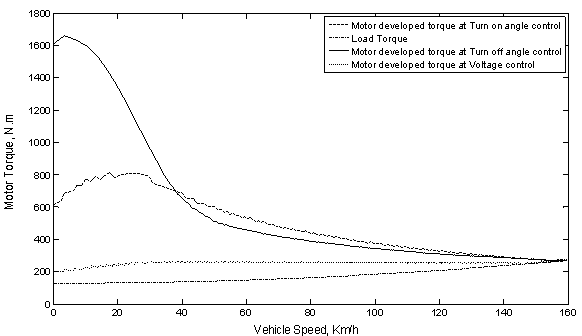
Figure 8. Motor developed torque and load torque versus vehicle speed at acceleration under the different control methods.

Using the motor developed torque, calculated from equation (11), and the motor speed, calculated from equation (12), into equation (20) the characteristics of the motor output power, P_mo, can be obtained and plotted against the vehicle speed, for the three cases of control illustrated earlier, as shown in Figure 9. From this figure it is noticed that the motor output power, for the case of turn off angle control, is decrease as the vehicle accelerates, up to 40 Km/h, and then the power increase as the vehicle speed increases but for the other cases of control the motor output power increase as the vehicle accelerates up to the final steady-state speed. At certain vehicle speed the motor output power, at the voltage control method, have the lower values than that of the other methods of control. Also the motor output power, at the turn off angle control method, have the highest values at the lower vehicle speed (< 40 Km/h) and the motor output power, at the turn on angle control method, have the highest values at the other values of vehicle speed.

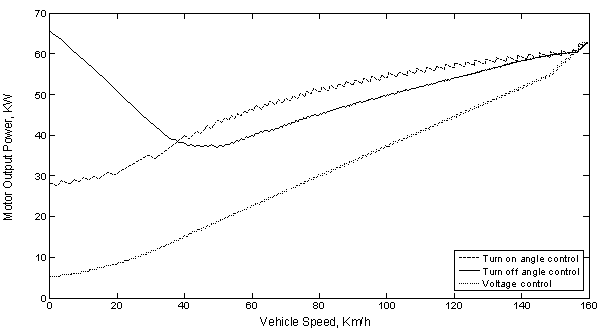
Figure 9. Motor output power versus vehicle speed at acceleration under the different control methods.

Using the values of the motor phase current, which are obtained into equation (21), the motor power losses, P_Loss, can be drawn versus the vehicle speed, during acceleration until steady-state conditions are reached, as shown in Figure 10. From this figure it is clear that the motor power losses, for the different methods of control, is maintained constant, due to the constancy of the phase current, as the vehicle accelerates up to the final steady-state speed. Using the predetermined motor phase current into equation (22), the motor excessive energy, E_exc, can be computed and plotted as shown in Figure 11. From this figure it is clear that at certain vehicle speed the motor excessive energy, at the turn off angle control method, have higher values than that of the other control methods during the vehicle acceleration. Also the values of the motor excessive energy, for the different methods of control, are very small thus it can be neglected.

Multiplying the predetermined motor phase current which is obtained at the two cases illustrated earlier, from equation (9) and (10), by the motor terminal voltage, the motor input power, P_{m_in}, can be also computed and plotted as shown in Figure 12. From this figure it is noticed that, for the case of turn off angle control, the motor input power has a higher value and then decrease as the vehicle speed increases and for the other cases of control the motor input power will increase as the vehicle accelerates up to the final steady-state speed at which the curves are intersected. At certain vehicle speed the motor input power, at the case of turn off angle control, have the highest values on the contrary the motor input power will have the lowest values at the voltage control method.

Figure 10. Motor power losses versus vehicle speed at acceleration under the different control methods.

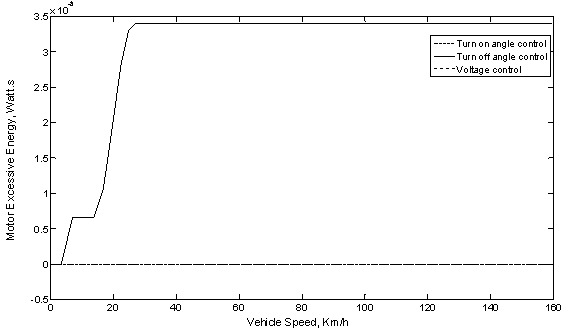
Figure 11. Motor excessive energy versus vehicle speed at acceleration under the different control methods.

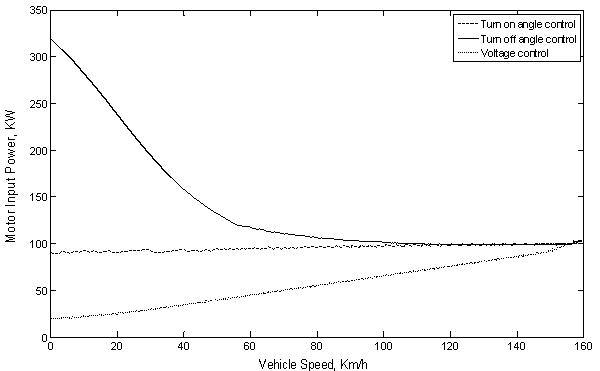
Figure 12. Motor input power versus vehicle speed at acceleration under the different control methods.

Using the values of the motor input power and the motor output power which are obtained previously, the characteristics of the motor efficiency, η_m, can be obtained against the vehicle speed as shown in Figure 13.

Figure 13. Motor efficiency versus vehicle speed at acceleration under the different control methods.

From this figure it is clear that, for the different methods of control, the motor efficiency is increase as the vehicle speed increases. At certain vehicle speed the motor efficiency, at the voltage control method, have the highest value especially at any vehicle speed higher than 25 Km/h and the motor efficiency, at the turn on angle control method, will have the largest value at other values of vehicle speed. But the motor efficiency at the case of turn off angle control always has the lower value during the acceleration period. Also the motor efficiency, at the voltage control method, have the highest value especially at any vehicle speed higher than 25 Km/h and the motor efficiency, at the turn on angle control method, will have the largest value at other values of vehicle speed. But the motor efficiency at the case of turn off angle control always has the lower value during the acceleration period.

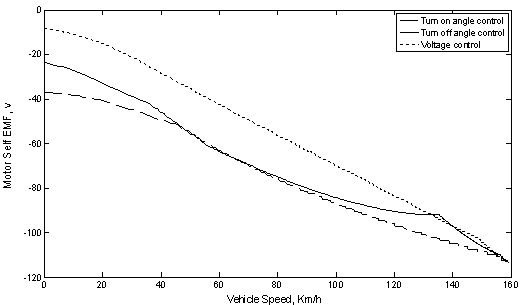
From equation (6) the motor rotational and self EMF can be calculated for the different cases of control illustrated previously. Then the rotational and self EMF is plotted versus vehicle speed as shown in Figures 14 and 15 respectively.

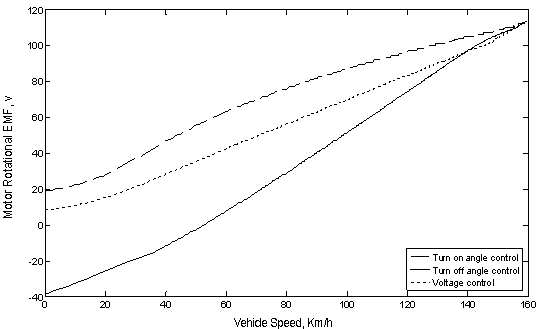
Figure 14. Motor rotational EMF versus vehicle speed at acceleration under the different control methods.

Figure 15. Motor self EMF versus vehicle speed at acceleration under the different control methods.

From Figure 14 it is clear that the motor rotational EMF increase as the vehicle speed increases for all the cases of control. Then at a certain vehicle speed the rotational EMF will have the larger values for the case of turn on angle control on contrary the rotational EMF having the lower values also for the case of turn off angle control especially at vehicle speed lower than 140 Km/h. Also from Figure 15 it is noticed that the motor self EMF, for the different cases of control, decrease as the vehicle accelerates up to the final steady-state speed. At a certain vehicle speed the self EMF will have the higher values at the case of voltage control on contrary the self EMF will have the lower values for the case of turn on angle control.

Conclusions

From the performance characteristics of the EV operating in the acceleration mode under the different methods of control it can be noticed that the acceleration time, for the case at which the turn on angle is controlled, will be smaller than that for the other cases also the acceleration time, for the case of voltage control, will be the largest.

Also the motor efficiency, at the voltage control method, have the highest value especially at any vehicle speed higher than 25 Km/h and the motor efficiency, at the turn on angle control method, will have the largest value at other values of vehicle speed. But the motor efficiency at the case of turn off angle control always has the lower value during the acceleration period.

List of symbols

Af	Equivalent frontal area of the vehicle in m^2.
C0	Coefficient of rolling resistance.
CD	Aerodynamic drag coefficient.
Eexc	Motor excessive energy.
FRL	Road load force in N.
FTR	Tractive force in N.
g	Gravitational acceleration constant in m/s^2.
i	Motor phase current
Iph	The average value of the motor phase current in A.
Ir	Rated value of the motor phase current in A.
k1… k4	Constants.
km	Rotational inertia coefficient.
L	Motor phase inductance.
La	Aligned inductance in mH.
Lu	Unaligned inductance in mH.
m	The gear ratio of the mechanical coupling between the motor and the axle of the vehicle wheels.
Mveh	Total mass of the vehicle in kg.
nph	Number of motor phases.
Nr	Number of rotor poles.
PLoss	Motor power losses in W.
Pmـin	Motor input power in W.
Pmo	Motor output power in W.
R	Motor phase resistance in ohm.
rwh	Radius of the wheel in m.
Tb	Frictional brake torque in Nm.
Td_wh	The developed torque at the shaft of the wheel axle
Te	Motor developed torque in Nm.
TL	Load torque at the shaft of the motor axle in Nm.
Twh	Load torque at the shaft of the wheel axle in Nm.
v	Motor phase voltage in v.
Vs	DC supply voltage in v.
Vveh	Vehicle speed in km/h.
β	Road grade angle.
βr	Rotor poles arc.
θ	Rotor position in elec.rad.
θ0	The angle at which the motor phase current equal zero after decaying.
θoff	Turn off angle.
θon	Turn on angle.
λ	Motor phase flux linkage.
ρ	Air density in kg/m^3.
ω	Motor speed in elec.rad/s.
ωm	Motor speed in rad/s.

Appendix

Data of the SRM: P_r =60 kW, V_r=280 V, R=0.072 ohm, L_a=3.334 mH, L_u=0.445 mH, N_r=4, N_s=6, n_ph =3, B_s=B_r=π/6, j=0.3, b=0.0183,_nr=2214 rpm

Vehicle dynamic parameters: ρ =1.225 kg/m³, C_D =0.3, A_f =2 m², M_veh =1500 kg, r_wh=0.2794 m, Tb=0, V_veh-max =160 km/h, V_f =100 km/h, k_m =1.08, C₀=0.01, g =9.81m/s², m=1.4575, β=2°. η_tmw =1.00.

References

1. Ehsani M., Rahman K.M., Toliyat H.A., Propulsion System Design of Electric and Hybrid Vehicles, IEEE Transactions on Industrial Electronics, 1997, 44(1), p. 19-27.

2. Husain I., Electric and Hybrid Vehicles Design Fundamentals, Taylor & Francis e-Library, 2005.

3. Ehsani M., Gao Y., Gay S.E., Emadi A., Modern Electric, Hybrid Electric, and Fuel Cell Vehicles Fundamentals, Theory, and Design, CRC Press LLC, 2005.

4. Husain I., Islam M.I., Design, Modeling and Simulation of an Electric Vehicle System, Society of Automotive Engineers (SAE), International Congress and Exposition, Detroit, Michigon, 1995, p. 1-9.

5. Khwaja M., Rahman, Fahimi B., Suresh G., Rajarathnam A.V., Ehsani M., Advantages of Switched Reluctance Motor Applications to EV and HEV: Design and Control Issues, IEEE Transactions on Industry Applications, 2000, 36(1), p. 111-121.

6. Sadeghi S., Milimonfared J., Mirsalim M., Dynamic Modeling and Simulation of a Series Hybrid Electric Vehicle Using a Switched Reluctance Motor, Proceeding of International Conference on Electrical Machines and Systems, Seoul Korea, 8-11 October 2007, p. 2017-2022.

7. Kachapornkul S., Jitkreeyarn P., Somsiri P., Tungpimolrut K., A Design of 15kW Switched Reluctance Motor for Electric Vehicle Applications, Proceeding of International Conference on Electrical Machines and Systems, Seoul, Korea, 8-11 October 2007, p. 1690-1693.

8. Cinar M.A., Erfan Kuyumcu F., Design and Drives Simulation of an In-Wheel Switched Reluctance Motor for Electric Vehicle Applications, IEEE International Electric Machines & Drives Conference (IEMDC '07), 3-5 May 2007, 1, p. 50-54.

9. Cui S., Yuan Y., Wang T., Research on Switched Reluctance Double-rotor Motor Used for Hybrid Electric Vehicle, IEEE International Conference on Electrical Machines and Systems (ICEMS), 17-20 October 2008, p. 3393-3396.

10. Aida S., Komatsuzaki A., Miki I., Basic Characteristics of Electric Vehicle Using 40kW Switched Reluctance Motor, IEEE International Conference on Electrical Machines and Systems (ICEMS), 17-20 October 2008, p. 3358-3361.

11. Xue X.D., Lin J.K., Zhang Z., Ng T.W., Luk K.F., Cheng K.W.E., Cheung N.C., Study of Motoring Operation of In-wheel Switched Reluctance Motor Drives for Electric Vehicles, 3rd IEEE International Conference on Power Electronics Systems and Applications (PESA), 20-22 May 2009, p. 1-6.

12. Lin J., Cheng K.W.E., Zhang Z., Xue X., Experimental Investigation of In-wheel Switched Reluctance Motor Driving System for Future Electric Vehicles, IEEE 3rd International Conference on Power Electronics Systems and Applications (PESA), 20-22 May 2009, p.1-6.

13. Xue X.D., Cheng K.W.E., Ng T.W., Cheung N.C., Multi-Objective Optimization Design of In-Wheel Switched Reluctance Motors in Electric Vehicles, IEEE Transactions on Industrial Electronics, 2010, 57(9), p. 2980-2987.