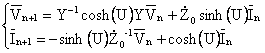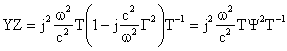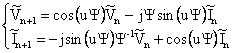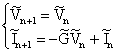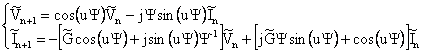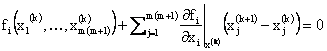Characteristic Impedance of Periodically Grounded Power Lines
Amedeo ANDREOTTI1*, Dario ASSANTE2, Renato RIZZO1,
and Antonio PIERNO1
1 Department of Electrical Engineering, University “Federico II”,Via Claudio 21, Naples, Italy
2 Department of Electrical Engineering, International Telematic University Uninettuno, Corso V. Emanuele II 39, Rome, Italy
E-mails: andreot@unina.it *; d.assante@uninettunouniversity.net ; renrizzo@unina.it ; antonio.pierno@unina.it
* Corresponding author: Phone: +39 081 7683215; Fax: +39 081 2396897
Abstract
In the paper the characteristic impedance of a multi-conductor transmission line with one conductor periodically grounded is evaluated. The topic is important in the analysis of the role of the shield wires in power transmission and distribution lines. The problem is here modelled in terms of a non-symmetric algebraic Riccati equation. Some applications will be presented.
Keywords
Transmission lines; Grounding; Characteristic impedance; Non-symmetric algebraic Riccati equation.
Introduction
The main role of periodically grounded wires in power lines is to intercept direct lightning strokes which could cause overvoltage’s higher than the line lightning withstand level. These wires, called shield wires, are installed above the phase conductors, and, if properly placed, assure a good lightning protection. It must be emphasized that this direct protection is successful on power transmission lines, which are usually characterized by values of critical impulse flashover voltage (CFO) much higher compared to distribution lines. The direct stroke performance of distribution lines is practically unaffected by the presence of shield wires, since, in case of a direct strike, a back flashover will occur in most of the cases, due to the ground potential rise. In distribution lines the shield wire can still play a role since, thanks to its coupling with the phase conductors, it can reduce the induced voltages caused by the nearby lightning electromagnetic fields. Many studies have dealt with the effectiveness of shield wires on medium and low voltage overhead distribution lines (e.g. in [1-7]) and the reduction in terms of induced overvoltage’s, compared to the results obtained for unshielded lines (e.g. [8-10]), is significant; the authors have also deeply investigated the problem of lightning induced overvoltage’s on unshielded lines [11-19].
In order to evaluate the induced overvoltage’s on shielded lines, and to estimate the role of the periodical grounding in the overvoltage mitigation, an important step is the evaluation of the characteristic impedance of the power line. Although periodical grounding of shield wires significantly modifies the characteristic impedance, this aspect is usually underestimated or neglected.
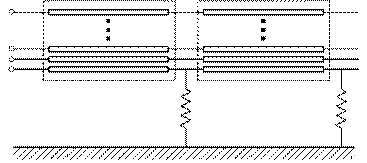
The aim of this paper was to determine the characteristic impedance, in case of a multi-conductor transmission line (MTL) problem, with one conductor periodically grounded, as shown in figure 1. The examined MTL has m-1 non-grounded wires; the m-th wire is the grounded one.
|
|
|
Figure 1. Line Configuration |
Problem Formulation
In order to compute the
characteristic impedance transmission line (TL) approximation [20] is applied
and two computation ways are presented. We define ![]() and
and ![]() the voltages and currents vectors of the
MTL, where z is the distance evaluated from the line origin. The most
relevant distances for observing voltages and currents are those corresponding
to each grounding point, we will call them
the voltages and currents vectors of the
MTL, where z is the distance evaluated from the line origin. The most
relevant distances for observing voltages and currents are those corresponding
to each grounding point, we will call them ![]() and
and ![]() with n = 0, 1, 2, …
and L is the distance between two following grounding points, i.e. the length
of an elementary MTL cell. Then we call as r, l and c the m×m
per unit length resistance, inductance and capacitance matrices of the MTL, and
define Z=r+jωl and Y = jωc. The characteristic impedance of a
non-grounded MTL is given by
with n = 0, 1, 2, …
and L is the distance between two following grounding points, i.e. the length
of an elementary MTL cell. Then we call as r, l and c the m×m
per unit length resistance, inductance and capacitance matrices of the MTL, and
define Z=r+jωl and Y = jωc. The characteristic impedance of a
non-grounded MTL is given by ![]() .
.
If we consider a single cell of a non-grounded MTL, its chain matrix can be expressed as in [21]:
|
|
(1) |
being ![]() .
.
Modal variables are commonly used in MTL theory in order to simplify the analysis. To this purpose we can consider a similarity transformation, in order to diagonalise the product YZ. Since in our case lc = 1/c2, being c the speed of light in vacuum, the only product cr has to be diagonalised. It is possible to introduce the similarity transformation matrix T so that T-1crT=Γ2, being Γ a diagonal matrix. Since c and r are real, symmetric and positive definite matrices, then T and Γ are real matrices. It is then possible to express the product YZ as:
|
|
(2) |
being 1 the identity matrix.
It is interesting to
note that for the special case of lossless conductors, Γ vanishes
and so Ψ is an identity matrix at every frequency. In this case the
best choice is![]() . Then we can define the modal
voltages and currents, given respectively by
. Then we can define the modal
voltages and currents, given respectively by ![]() and
and ![]() , that turn (1) into:
, that turn (1) into:
|
|
(3) |
being u=Lω/c.
The transformation in (3) decouples the chain matrix equations and simplifies the following calculations. It is worth noting that in the modal domain the characteristic impedance matrix of the non-grounded MTL becomes a diagonal matrix too, and in particular:
|
|
(4) |
The chain matrix at the grounding point is in the modal domain:
|
|
(5) |
being ![]() , and G an m×m matrix where all
the elements are zero but the last one, Gm,m=1/Rg,
being Rg the grounding resistance. While G is almost
an empty matrix,
, and G an m×m matrix where all
the elements are zero but the last one, Gm,m=1/Rg,
being Rg the grounding resistance. While G is almost
an empty matrix, ![]() is a singular real positive
full matrix. So the chain matrix of a single cell of a grounded MTL is given by
the product of the chain matrices (3) and (5), obtaining:
is a singular real positive
full matrix. So the chain matrix of a single cell of a grounded MTL is given by
the product of the chain matrices (3) and (5), obtaining:
|
|
(6) |
It is possible to define
![]() as the characteristic
impedance matrix of the periodically grounded MTL in the modal domain, related
to the actual characteristic impedance matrix by the relation
as the characteristic
impedance matrix of the periodically grounded MTL in the modal domain, related
to the actual characteristic impedance matrix by the relation ![]() according to (4). Being the structure
semi-infinite, it is clear that voltages and currents are linked by the
relation
according to (4). Being the structure
semi-infinite, it is clear that voltages and currents are linked by the
relation ![]() , for every i = 0, 1, ... .
Enforcing this relation in (6), and considering that it has to be valid for
every set of voltages and currents, by some manipulations it is possible to
obtain a second order equation where the only unknown is
, for every i = 0, 1, ... .
Enforcing this relation in (6), and considering that it has to be valid for
every set of voltages and currents, by some manipulations it is possible to
obtain a second order equation where the only unknown is ![]() , namely:
, namely:
|
|
(7) |
where:
|
|
(8) |
|
|
(9) |
|
|
(10) |
|
|
(11) |
This equation is a non-symmetric algebraic Riccati equation (NARE) with complex coefficients, probably one of the worst cases among the Riccati equations. Such a problem has been widely studied in literature and some methods have been proposed to solve it numerically [22, 23]. Before presenting solution methods for this equation, a consideration on the MTL per unit length parameters frequency dependence has to be done. If we suppose that the three parameters are frequency independent, the diagonalization matrix T is frequency independent too. The diagonalization of YZ has to be performed just once and the method can be applied easily. A frequency dependence of the line parameters can be introduced anyway with minimum effort, for instance to take into account the skin effect into r. In this case the proposed method can be applied as well, but the diagonalization matrix T is frequency dependent and so the diagonalization of YZ has to be repeated at each frequency step.
Solution of the Riccati Equation
Now we will present two
ways of solving the Riccati equation, which will then be implemented; the first
one is an iterative algorithm based on a Newton-Raphson method [24-26], the
second method leads to a straight-forward computation of the solution by means
of the decomposition of the Hamiltonian matrix of the equation [27]. In order
to implement the iterative algorithm based on a Newton-Raphson method, it is
preferable to operate with real equations. By introducing the unknown
resistance and reactance matrixes from ![]() , the NARE (7) can be split into two second
order matrix equations. If the line has m conductors, 2m2
real equations are obtained by this process. Anyway, due to the reciprocity of
the characteristic impedance matrix and so to its symmetry, only m(m+1)
equations are needed. If we consider a general equation:
, the NARE (7) can be split into two second
order matrix equations. If the line has m conductors, 2m2
real equations are obtained by this process. Anyway, due to the reciprocity of
the characteristic impedance matrix and so to its symmetry, only m(m+1)
equations are needed. If we consider a general equation:
|
|
(12) |
an iterative procedure can be set-up as follow:
|
|
(13) |
Since the equations include quadratic terms at most, the computation of the derivatives is simple. In a frequency sweep, the best starting point for the iteration at a given frequency is the solution found at the previous frequency step, adopting a step frequency not so large compared to the variations of the characteristic impedance. In case of single frequency, the starting point has to be considered carefully since the problem admits multiple solutions. The second method refers to non-iterative methods. Most of them are based on the decomposition of the Hamiltonian matrix of the problem. The Hamiltonian matrix of (7) is defined as:
|
|
(14) |
If it possible to decompose the Hamiltonian matrix as:
|
|
(15) |
if the matrix U is partitioned as 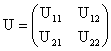 and U11 is non-singular, then
the solution of the (7) is obtained as:
and U11 is non-singular, then
the solution of the (7) is obtained as:
|
|
(16) |
This result can be
proved since ![]() is an invariant subspace of H.
The decomposition (15) can be performed in different ways; a diagonalization of
H is the preferable solution since it doesn’t require a significant
computational effort. More generally Jordan decomposition can be adopted; this
method includes also the cases when H cannot be diagonalized. Schur
decomposition can be used as well, but it requires higher computational effort,
however, the algorithms are more stable than the ones implementing the Jordan
decomposition. In order to analyse and evaluate these methods, some numerical
simulations are now performed. The line geometry considered for the numerical
simulations is a two-conductor line made by a non-grounded wire at a height of
14.8m, located beneath a periodically grounded wire at a height of 16m (these
are typical heights of an Italian power transmission line). The cross section
and the per-unit length resistivity are 148.5 mm2 and 0.2282
Ω/km respectively, for the grounded cable, and 227.8 mm2 and
0.1576 Ω/km for the lower cable. A reference length L=100m is assumed
between two following grounding points. A grounding resistance of 1Ω,
10Ω and 100Ω has been considered. The characteristic impedance has
been computed by both methods, and relative difference between the two is
always lower than 1·10-13, that proofs that the two methods give
practically the same solution. Further, by substituting the solutions into (7),
the norm of the residue is lower than 4·10-13 compared to the norm
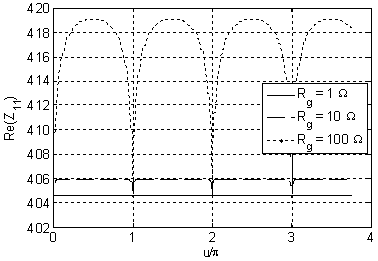
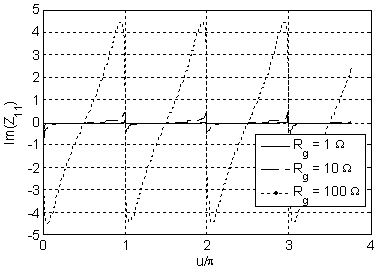
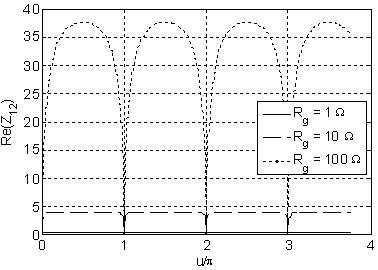
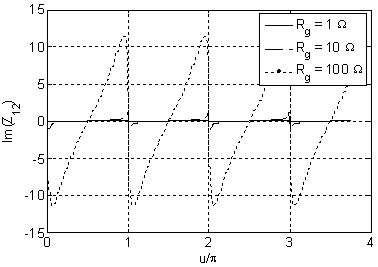
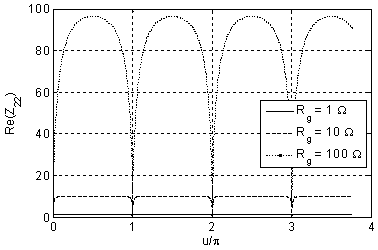
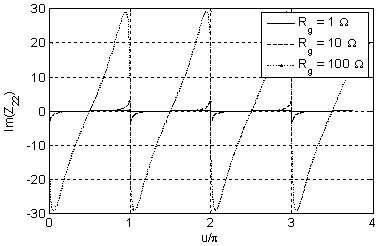
of the solution and that proves the correctness of the solution. In figures 2-7
the real and imaginary parts of the different terms of the characteristic
impedance are presented, as function of the frequency and for different values
of the grounding resistance.
is an invariant subspace of H.
The decomposition (15) can be performed in different ways; a diagonalization of
H is the preferable solution since it doesn’t require a significant
computational effort. More generally Jordan decomposition can be adopted; this
method includes also the cases when H cannot be diagonalized. Schur
decomposition can be used as well, but it requires higher computational effort,
however, the algorithms are more stable than the ones implementing the Jordan
decomposition. In order to analyse and evaluate these methods, some numerical
simulations are now performed. The line geometry considered for the numerical
simulations is a two-conductor line made by a non-grounded wire at a height of
14.8m, located beneath a periodically grounded wire at a height of 16m (these
are typical heights of an Italian power transmission line). The cross section
and the per-unit length resistivity are 148.5 mm2 and 0.2282
Ω/km respectively, for the grounded cable, and 227.8 mm2 and
0.1576 Ω/km for the lower cable. A reference length L=100m is assumed
between two following grounding points. A grounding resistance of 1Ω,
10Ω and 100Ω has been considered. The characteristic impedance has
been computed by both methods, and relative difference between the two is
always lower than 1·10-13, that proofs that the two methods give
practically the same solution. Further, by substituting the solutions into (7),
the norm of the residue is lower than 4·10-13 compared to the norm
of the solution and that proves the correctness of the solution. In figures 2-7
the real and imaginary parts of the different terms of the characteristic
impedance are presented, as function of the frequency and for different values
of the grounding resistance.
|
|
|
Figure 2. Real part of |
|
|
|
Figure 3. Imaginary part of |
|
|
|
Figure 4. Real part of |
|
|
|
Figure 5. Imaginary part of |
|
|
|
Figure 6. Real part of |
|
|
|
Figure 7. Imaginary part of |
By making the different simulations, we observe an important result: either including or omitting the per unit length resistance in the MTL parameters has no observable effects on the characteristic impedance. The significant result is that we can always simplify the problem by considering the line as lossless. From a strict mathematical point of view, we observe that for p.u.l. resistances higher than 10 Ω/km differences show up for the characteristic impedance, but these values are not realistic and so we can absolutely consider the MTL as lossless.
Conclusions
The problem of the characteristic impedance of a multi-conductor transmission line with one conductor periodically grounded has been discussed and formulated in terms of a NARE equation. Two methods have been presented and applied in order to solve the equation. Further investigations are required to test and compare the robustness and efficiency of the two methods for more complex MTL configurations.
References
1. Rusck S., Induced lightning over-voltages on power-transmission lines with special reference to the over-voltage protection of low voltage networks, Transactions of the Royal Institute of Technology, 1958, 120, p. 1-75.
2. Piantini A., Lightning protection of overhead power distribution lines, Proceedings of the 29th International Conference on Lightning Protection (ICLP), Uppsala, Sweden, 2008, p. 1-29.
3. Chowdhuri P., Lightning-induced voltages on multiconductor overhead lines, IEEE Trans. Power Delivery, 1990, 5(2), p. 658-667.
4. Rachidi F., Nucci C.A., Ianoz M., Transient analysis of multi-conductor lines above a lossy ground, IEEE Trans. Power Delivery, 1999, 14, p. 294-302.
5. Rachidi F., Nucci C.A., Ianoz M., Mazzetti C., Response of multiconductor power lines to nearby lightning return stroke electromagnetic fields, IEEE Trans. Power Delivery, 1997, 12, p. 1404-1411.
6. Paolone M., Nucci C.A., Petrache E., Rachidi F., Mitigation of lightning-induced overvoltages in medium voltage distribution lines by means of periodical grounding of shielding wires and of surge arresters, modeling and experimental validation, IEEE Trans. Power Delivery, 2004, 19(1), p. 423-431.
7. Borghetti A., Nucci C.A., Paolone M., An improved procedure for the assessment of overhead line indirect lightning performance and its comparison with the IEEE Std. 1410 Method, IEEE Trans. Power Delivery, 2007, 22(1), p. 684-692.
8. Rachidi F., Nucci C.A., Ianoz M., Transient analysis of multiconductor lines above a lossy ground, IEEE Trans. Power Delivery, 1999, 14(1), p. 294-302.
9. Hoidalen H.K., Slebtak J., Henriksen T., Ground effects on induced voltages from nearby lightning, IEEE Trans. Electromagn. Compat., 1997, 39(4), p. 269-278.
10. Diendorfer G., Induced voltage on an overhead line due to nearby lightning, IEEE Trans. Electromagn. Compat., 1990, 32(4), p. 292-299.
11. Andreotti A., Assante D., Mottola F., Verolino L., An exact closed-form solution for lightning-induced overvoltages calculations, IEEE Trans. Power Delivery, 2009, 24(3), p. 1328-1343.
12. Andreotti A., Petrarca C., Rakov V.A., Verolino L., Calculation of voltages induced on overhead conductors by nonvertical lightning channels, IEEE Trans. Electromagn. Compat., 2012, 54(4), p. 860-870.
13. Andreotti A., De Martinis U., Petrarca C., Rakov V.A., Verolino L., Lightning electromagnetic fields and induced voltages: Influence of channel tortuosity, Proceedings of the 30th URSI General Assembly and Scientific Symposium (URSI GASS), Istambul, Turkey, 2011, p. 1-4.
14. Andreotti A., Pierno A., Rakov V.A., Verolino L., Analytical formulations for lightning-induced voltage calculations, IEEE Trans. Electromagn. Compat., 2013, 55(1), p. 109-123.
15. Andreotti A., Del Pizzo A., Rizzo R., Verolino L., Lightning induced effects on lossy multiconductor power lines with ground wires and non-linear loads - Part I: model, Przeglad Elektrotechniczny (Electrical Review), 2012, R88(9b), p. 301-304.
16. Andreotti A., Del Pizzo A., Rizzo R., Verolino L., Lightning induced effects on lossy multiconductor power lines with ground wires and non-linear loads - Part II: simulation results and experimental validation, Przeglad Elektrotechniczny (Electrical Review), 2012, R88(9b), p. 305-309.
17. Ceclan A., Ţopa V., Micu D. D., Miron O., Czumbil L., Numerical Tools for Lightning Return Stroke Current Reconstruction by Electromagnetic Inverse Problem Formulation, Proceedings of the 3rd International Conference on Clean Electrical Power (ICCEP), Ischia, Italy, 2011, p. 293-298.
18. Ceclan A., Micu D.D., Czumbil L., On a return stroke lightning identification procedure by inverse formulation and regularization, The 14th Bienial IEEE Conference on Electromagnetic Field Computation (CEFC), Chigaco, USA, 2010.
19. Ceclan A., Ţopa V., Micu D.D., Czumbil L., On an Inverse Electromagnetic Procedure for Frequency and Spatial Reconstruction of the Lightning Return Stroke Current, 8th International Conference on Computational Electromagnetics (CEM), Wroclaw, Poland, 2011.
20. Andreotti A., Assante D., Rakov V.A., Verolino L., Electromagnetic Coupling of Lightning to Power Lines: Transmission-Line Approximation versus Full-Wave Solution, IEEE Trans. Electromagn. Compat., 2011, 53(2), p. 421-428.
21. Paul C.R., Analysis of multiconductor transmission lines, Wiley-Interscience, New York, USA, 2008.
22. Freiling G.A., A survey of nonsymmetric Riccati equations, Linear Algebra and its Applications, 2002, 351-352, p. 243-270.
23. Dattoli G., Ricci P.E., Cesarano C., Special polynomials and associated differential equations from a general point of view, International Mathematical Journal, 2003, 4, p. 321-328.
24. Lu L.Z., Newton iterations for a non-symmetric algebraic Riccati equation, Numerical Linear Algebra with Applications, 2005, 12, p. 191-200.
25. Bini D.A., Iannazzo B., Poloni F., A fast Newton’s method for a nonsymmetric algebraic Riccati equation, SIAM J. Matrix Anal. Appl., 2009, 30(1), p. 276-290.
26. Micu D.D., Czumbil L., Christoforidis G., Ceclan A., Layer Recurrent Neural Network Solution for an Electromagnetic Interference Problem, IEEE Transaction on Magnetics, 2011, 47(5), p.1410-1414.
27. Guo X.X., Bai Z.Z., On the minimal nonnegative solution of nonsymmetric algebraic Riccati equation, J. Comput. Math., 2005, 23, p. 305-320.