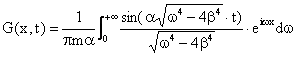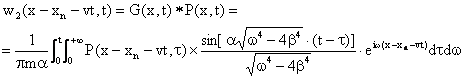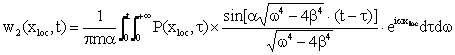Analytical Model of Underground Train Induced Vibrations on Nearby Building Structures in Cameroon: Assessment and Prediction
Lezin Seba MINSILI1*, He XIA2 and Robert Medjo EKO3
1 LMMC-GC, National Polytechnic Advanced School, The University of Yaoundé I, Cameroon
2 School of Civil Engineering & Architecture, Beijing Jiaotong University, Beijing. China
3 Department of Earth Science, Faculty of Science, The University of Yaounde I, Cameroon
E-mails: lezinsm@yahoo.com*; hxia88@163.com; rmedjo@yahoo.com
* Corresponding author: Phone: +237-77922659
Abstract
The purpose of this research paper was to assess and predict the effect of vibrations induced by an underground railway on nearby-existing buildings prior to the construction of projected new railway lines of the National Railway Master Plan of Cameroon and after upgrading of the railway conceded to CAMRAIL linking the two most densely populated cities of Cameroon: Douala and Yaoundé. With the source-transmitter-receiver mathematical model as the train-soil-structure interaction model, taking into account sub-model parameters such as type of the train-railway system, typical geotechnical conditions of the ground and the sensitivity of the nearby buildings, the analysis is carried out over the entire system using the dynamic finite element method in the time domain. This subdivision of the model is a powerful tool that allows to consider different alternatives of sub-models with different characteristics, and thus to determine any critical excessive vibration impact. Based on semi-empirical analytical results obtained from presented models, the present work assesses and predicts characteristics of traffic-induced vibrations as a function of time duration, intensity and vehicle speed, as well as their influence on buildings at different levels.
Keywords
Railway; Train; Track; Vibration; Building; Dynamic load; Sub-model; Acceleration.
Introduction
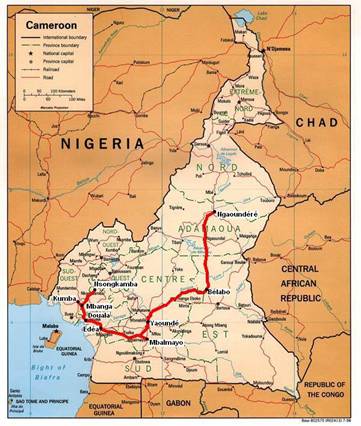
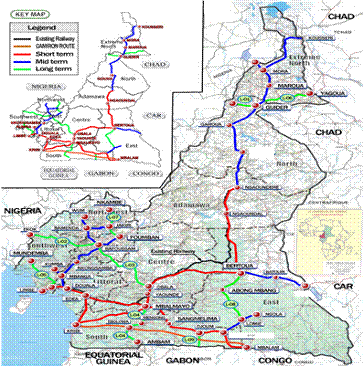
In 2008, the Cameroon government announced its long-term vision for vitalizing the economy and developing the nation into a newly industrialized country by the year of 2035. Among a number of strategies devised to bolster the industry, the need to expand transport infrastructures, which constitute a major hindrance in its economic progress despite a rich reserve of mineral resources, such as diamonds, iron and bauxite. Research conducted by international organizations such as the World Bank or the United Nations [1] also concludes that the railway network must be modified and renewed for Cameroon’s economic development. Cameroon government must lose no time in reforming the railway network in order to maximize the country’s potentials, as the overall backwardness of the national economy is undermining the effectuality of Cameroon’s rich mineral resources. As a result, the Cameroon government requested a Korean Consortium KORPEC to conduct a prefeasibility study leading to the establishment of a National Railway Master Plan (NRMP) [2], worth of 3200 km new railway lines to be constructed (Figure 1), with the aim of revitalizing the national economy and reinforcing its global competitiveness.
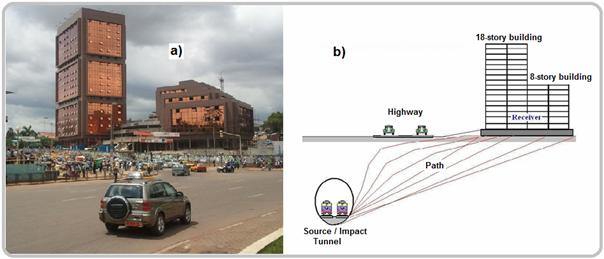
The appearance of industrial projects induced by economic boosting in Cameroon has thus resulted to a noticeable growth in new or upgraded transport infrastructures. This position involves the impact assessment on existing building structures of upgraded transport facilities and equipments, or the prediction of the behaviour of a new structure prior to its construction in the vicinity of existing transport infrastructures. Since the behaviours of buildings excited by rail traffic are almost the same, if not more pronounced, as when excited by road traffic, railway induced vibrations may have the following same effects: resonances in buildings or in parts of the buildings; directly radiated noise causing objects to rattle; dynamic consolidation of subsoil; and spatial variation of dynamic ground motion effects [3-5]. The problem that is solved in this paper a theoretical model of the Train-Soil-Structure (TSS) interaction described in Figure 2. Vibration transmission, from a place of emission (source) to the structure to be protected (receiver) through the soil layers (path) as seen in Figure 2.b, gives a way to the prediction or the measure of their effect on surrounding structures, and thus to the implementation of adequate regulations and protective and mitigation measures at the source, the path or the receiver.
|
a) Existing network [2]
b) Projected network [2] |
|
Figure 1. Projected Cameroon’s National Railway Network |
|
a) An abandoned 18-floor story building; b) Model of the TSS interaction |
|
Figure 2. Graphical description of the TSS interaction |
The aim of the research was to implement in Cameroon a sound expertise and a lasting experience in making predictions about ground-borne vibration. The model adopted in this work was used by Xia He [6], which has been presented in form of an equation containing the needed parameters to be used for different types of trains on different soil conditions. The geometry of the model and its parameters are chosen so that the most important aspects of the issue are considered without making the model too complicated or impractical [7]. Numerical results obtained from the model in the vertical plane allows to predict accelerations as the main vibration characteristics at any location from the railway track and at any floor level of the structure taken as an 18-story unused building located above the vicinity of a railway tunnel as seen in Figure 2.
Dynamic Load of Metro Train
Analytical Model of Metro Train-Track-Tunnel System
The train track system receives the load from the wheels, and then transfers it to the substructure. The load includes two parts: the vertical moving constant load (i.e. axle load) and the dynamic load produced by wheel-rail contact. To simplify the analytical model, the following hypotheses are made:
(1) Because the vertical excitation applied to the substructure by the running train is much larger than the horizontal excitation, the analysis is carried through only in the vertical plane.
(2) The rail is simulated as a continuous Euler-Bernoulli beam.
(3) The wheel-rail interaction is obtained by using the Hertzian contact theory, in which the Hertzian contact coefficient is expressed as kH.
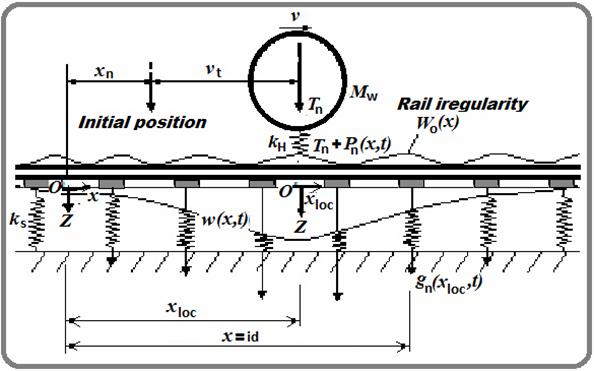
(4) For simplicity, the irregularity curve is thought of as a sine wave profile:
|
|
(1) |
where: w0(x) = the rail irregularity profile at the position of x, a = the maximum amplitude of rail irregularity, and l = its wavelength.
(5) Because the effective length of the rail deflection is usually much larger than the sleeper distance, the periodic support of sleepers to rails is reasonably neglected in this model [8], though in fact the rails are supported by a series of sleepers with equal space.
(6) The coupling between the track and the tunnel structure is simulated by springs. The spring stiffness ks are called the distributed track spring stiffness [9-10], whose value is equal to the support stiffness of the rails divided by the sleeper distance. And the support stiffness of the rails is expressed by the series-wound stiffness of the rail fastener stiffness, elastic pads stiffness, sleeper stiffness and roadbed-tunnel liner stiffness.
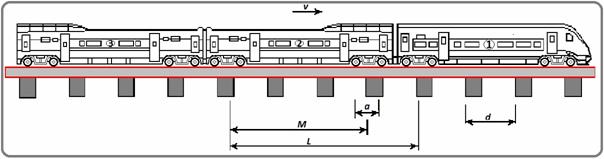
According to the above assumptions, the analytical model of metro train-track-tunnel system is established, as is shown in figure 3.
Rail Dynamic Deflection Induced by Single Wheel
Since the load applied to the rail is moving along x axle with the train speed v, the rail deflection curve cannot be static but a kind of dynamic deflection curve like a wave moving along x axle with the speed v, as is showed in figure 3(b). In this model, N specifies the total number of the wheels; Tn and xn are respectively the constant load amplitude and its initial position of the n-th wheel. Based on the theory of Euler-Bernoulli beam, the rail dynamic deflection w(x,t) induced by single wheel is governed by the following partial differential equation:
|
|
(2) |
where: EI = the rail bending stiffness and m0 = the rail mass per unit length (sleepers included); x = the horizontal distance of the constant load, Tn = away from coordinate origin during the process of moving and Pn(x,t) = the dynamic contact force between wheel and rail [11].
|
a) Geometrical parameters of train and track
(b) Interaction model of metro train-track-tunnel |
|
Figure 3. Analytical model of metro train-track-tunnel system |
The initial condition is:
|
|
(3) |
Also the boundary condition at the infinity is:
|
|
(4) |
Firstly, the rail static deflection curve is expressed. When the train is static, the load applied to the rail is static constant axle load Tn. Correspondingly the rail deformation is described as a static deflection curve [12-13]:
|
|
(5) |
where: the superscript st denotes the static solution and ![]() . It can be seen
from this equation that the effective length of rail deflection curve is
. It can be seen
from this equation that the effective length of rail deflection curve is ![]() .
.
Equation (2) shows that the dynamic deflection is induced by two kinds of loads: the moving constant load and the moving dynamic load. The solution thus consists of two parts corresponding to the two loads.
For the moving constant load![]() , based on
Equation (5), the dynamic deflection curve can be easily expressed as follows:
, based on
Equation (5), the dynamic deflection curve can be easily expressed as follows:
|
|
(6) |
where: ![]() and
and ![]() , with
, with ![]() the velocity of free track waves.
the velocity of free track waves.
For the moving dynamic load![]() , the Green
function of the rail dynamic deflection induced by unit impulse load is
introduced first. The dynamic deflection of the rail under unit impulse load
is:
, the Green
function of the rail dynamic deflection induced by unit impulse load is
introduced first. The dynamic deflection of the rail under unit impulse load
is:
|
|
(7) |
By using the Laplace transformation, Fourier transformation and their corresponding inverse transformations, the final solution of the Green function Equation (7) can be solved as:
|
|
(8) |
where: ![]() and
and ![]() .
.
Based on the generalized Duhamel integral, the rail
dynamic deflection curve under the moving dynamic load ![]() can be
expressed as:
can be
expressed as:
|
|
(9) |
Therefore, the total dynamic deflection of the rail is the summation of the above two deflections:
|
|
(10) |
Since the load applied to rail is moving along x axle with the speed v, by introducing the local coordinate system xloc = x-xn-vt, the dynamic deflection of the rail induced by single wheel can be expressed as:
|
|
(11) |
where:
|
|
(12) |
|
|
(13) |
Dynamic Load Applied onto Tunnel
As shown in figure 3(b), the downward force transferred
onto the tunnel from each sleeper equals to the upward spring force bore on
this sleeper width, expressed as f(t)=ks·Δd·w(xloc),
herein Δd is the sleeper width, and its acting point lies under the
sleeper. On the other hand, it is not all sleepers but a certain number of
sleepers at the range of the deflection curve effective length that are
involved in the distribution of this force endured by the rail. These involved
sleepers are called the effective sleepers, and if Neff denotes the
number of effective sleepers, it can be seen from the model figure that ![]() .
.
In order to eliminate Δd from the expression of
f(t), the rail static deflection equation (7) is integrated along x, in which
the influence of m0g is neglected considering that m0g is
much smaller than Tn. Due to the non-continuous support of actual
sleepers, the integral can be written as the summation of Neff
integrals and so there is the expression of ![]() . The
substitution of it into f (t) results in:
. The
substitution of it into f (t) results in:
|
|
(14) |
If gn(xloc,t) is used to denote the dynamic load at the point of xloc applied onto tunnel by the n-th wheel, the following solution can be obtained by all the above derivations:
|
|
(15) |
where: δ function is introduced to explain that the acting point of this force is below under the sleeper, n = the serial number of the wheel, and i = the serial number of the sleeper corresponding to the force position.
The final dynamic force F(x,t) applied onto the tunnel by all the N wheels can be obtained by means of the superposition principle (the original coordinate system is reverted):
|
|
(16) |
Substitute Equation (15) into Equation (16), the following expression can be obtained:
|
|
(17) |
Discrete Dynamic Model of the System
Ground-born vibrations are the result of the train-track structure exciting the tunnel and adjacent soil layers, and creating waves that propagate to the foundations of nearby buildings. These received vibrations at the foundation propagate throughout other parts of the building structure [14-19] are showing that the ground-borne vibration due to wheel-tract trains is function of the geology condition, the covering depth, the train-track system. Since the response from this vibration input depends on building structural characteristics, the dynamic model is subdivided into different sub-models: the train model, the track model and the building model.
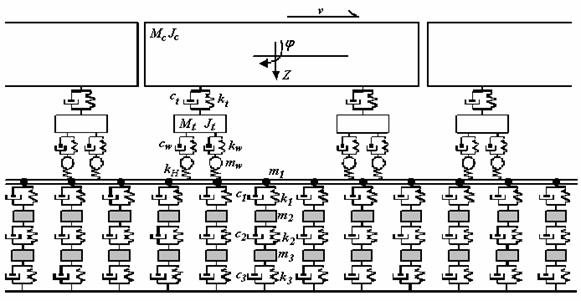
The train model is composed by a series of wagons, each consisting of car body, bogies, wheel sets, springs and dashpots. To simplify to analysis, the following hypotheses developed by Xia [20] are made on the vehicle: (1) car bodies, bogie frame and wheel sets are rigid without elastic deformation; (2) all dampers are viscous; (3) lateral movements and vertical movements of the vehicles are not coupled with each other. Thus there are two degrees of freedom (DOF) (floating and nodding) for each car body and bogie, represented by Zc, φc, and ZT, φT respectively, and one DOF for each wheel set (floating Zw). The total DOF number for a 4-axle train vehicle therefore is ten.
The track model consists of rail and rubber pads as seen in figure 4. The assumptions for the track model are: (1) the rail is taken as an endless beam on elastic supports, its mass and stiffness matrix in the dynamic equations, while the damping matrix is formed by the assumption of Rayleigh damping; (2) the stiffness and damping of the pads and fasteners are simplified into a set of compound masses, springs and dampers, represented by mi, ki and ci respectively; (3) The analysis is carried out only in the vertical plane. According to these assumptions, there are 2 DOFs (vertical displacement and rotation) for each rail node and one DOF (vertical movement) for each mass in the elastic support. The total number of DOF of the system therefore is 2N+2n, where N is the number of rail nodes and n is the number of elastic supports sets.
|
|
|
Figure 4. Dynamic model of Train-track system |
From the assumptions made above, the FE dynamic equilibrium equations of the train and the rail track is assembled into a single relation, and the global equilibrium equation of the train-rail track system is obtained as:
|
|
(18) |
Or in matrix form:
|
|
(19) |
Where the wheel-rail contact force F(x,t) is calculated using the Hertzian contact theory by using the discrete form of the Train-rail track interaction along the rail axis given as:
|
|
(20) |
where: Zwj(t) = the wheel displacement; v(x,t) = the rail
deflection at the wheel-rail contact point; δ(x) = the wheel or rail
profile change; kH = the Hertzian contact coefficient; n = the
number of vehicles; Mi = the mass matrix of the i-th vehicle (being
a diagonal matrix we have Diag Mi=[Mc, Jc, MT1,
MT2, JT2, Mw1, … , Mw4]); Ki
= the vehicle stiffness matrix, and Ci = the damping matrix; {Zi}
is the vehicle displacement vector; Fi is the force vector of the
i-th vehicle; Mn, Cn, Kn are respectively the
mass, damping and the stiffness matrices of the track; ![]() are respectively the nodal
acceleration, velocity and displacement vectors as given in the FE dynamic
equation; øij is the distributive coefficient of the j-th wheel-set
to the i-th rail node.
are respectively the nodal
acceleration, velocity and displacement vectors as given in the FE dynamic
equation; øij is the distributive coefficient of the j-th wheel-set
to the i-th rail node.
Simulation and Analysis of the TSS Interaction
Simulation by the FEM
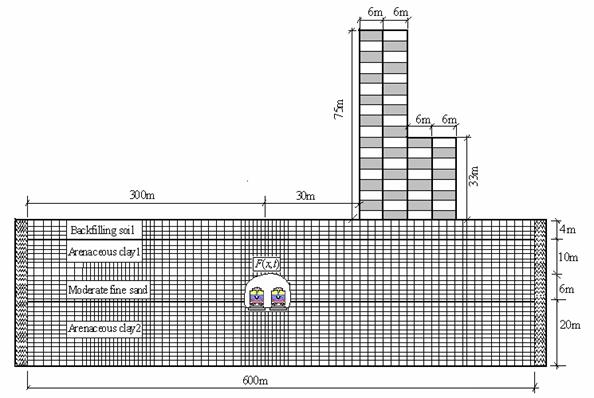
The FEM is the most widely used numerical method implemented by researchers and commercial software producers. It can be used to solve complex geometries, but it requires an appropriate discrete form of the media being modelled. This makes the FEM computationally unfeasible for very large scale models, such as those involving unbounded domains, unless substantial shortcuts are implemented. These may entail the use of coarse elements, low frequency simulations, or the introduction of boundary artefacts [21]. This not being the case of the present work since the soil sub domain and the building sub domain are bounded with appropriate boundary conditions as seen in the FE element model of the tunnel-soil-building system shown in figure 5 assuming a 2-D plane strain state. The double-track is inside the single hollow tunnel with a dimension of 10m (height) ×12m (width) and with 14m cover depth. The soil is divided into four layers, with their parameters shown in Table 1. An 18-story building is set at 30m from the tunnel centreline, which has the pile foundation with 15m length and whose members are all simulated as beam elements.
|
|
|
Figure 5. Finite element model of tunnel-soil-building system |
Table 1. Parameters of the building and sub soils
|
Materials |
Elastic modulus [MPa] |
Poisson ratio |
Density [N·m-3] |
Remarks |
|
C30 Concrete |
30000 |
0.18 |
2550 |
Beam (0.3m×0.6m), Columns (0.6m×0.6m) |
|
Backfilling soil |
29 |
0.40 |
17000 |
|
|
Arenaceous clay 1 |
127 |
0.33 |
18800 |
|
|
Moderate fine sand |
136 |
0.37 |
20200 |
|
|
Arenaceous clay 2 |
77 |
0.28 |
20000 |
|
The vibration evaluation method is settled in accordance with ISO2631/1-1985 that adopts the vertical acceleration level in terms of Lz=20log10(a/a0), where a is transient acceleration of the observation points with the unit of m/s2, and a0 is the basic acceleration with the value of 1×10-5m/s2. Since the model is asymmetric the whole system must be analyzed and the FE model should be as large as possible to contain the train length and to reduce the effect of the wave reflection at the artificial border. In this analysis, the model covers a dimension of 650m×80m. The bottom is assumed to have fixed constraints and the two sides are spring elements with the stiffness of 500kN/m.
The damping behaviour of each basic component j of the rail track-ground system was modelled using the Rayleigh method. The damping matrix C can be obtained from the relation:
|
|
(21) |
where: Mj and Kj are the j-th components of the mass and the stiffness matrices (respectively). Determination of the parameters αj and βj (as example αj =0.04 and βj =0.01) was carried out using the procedure described by Di Mino [22].
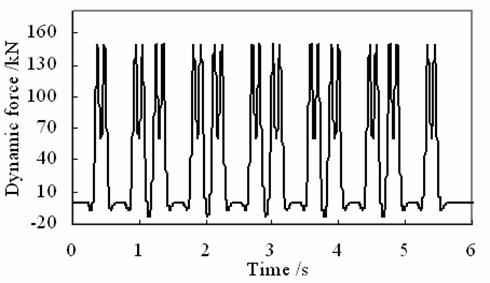
A train composed of 6 cars running on a track of continuous welded rails of 50 kg/m is considered. The mass of concrete sleeper is 251 kg, and the sleeper space is d=0.55m. The distributed rail spring stiffness is ks=202.46 MN/m2, and the wheel-rail contact stiffness coefficient is kH=1421MN/m. Implementing the theory and model described above with the vehicle and track parameters listed in table 2, the dynamic loads applied to the tunnel is obtained as shown in figure 6.
Table 2. Calculation parameters of underground vehicle
|
Vehicle full length L(m) |
19.52 |
|
Bogie centrelines’ distance 2s(m) |
12.66 |
|
Fixed axle spacing 2d(m) |
2.30 |
|
Car body mass Mc(t) |
37 |
|
Car mass moment of inertia Jc (t-m2) |
1700 |
|
Bogie mass Mt(t) |
3.60 |
|
Bogie mass moment of inertia Jt(t-m2) |
9.62 |
|
Bogie spring stiffness Kt (kN/m) |
2080 |
|
Bogie damping coefficient Ct (kNs/m) |
240 |
|
Wheel set mass Mw (t) |
1.70 |
|
Wheel spring stiffness (kN/m) |
2450 |
|
Wheel damping coefficient Kw (kNs/m) |
240 |
|
a) Dynamic load of train-track system
b) The spectrum of the train-track dynamic load |
|
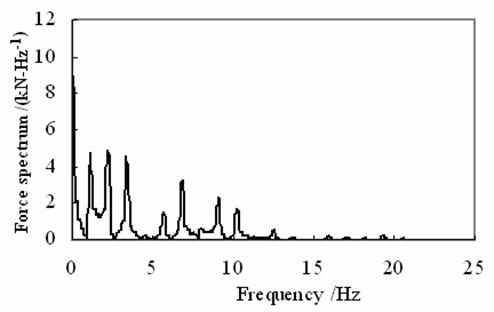
Figure 6. Characteristics of the dynamic load applied to the tunnel |
Analytical Results
The previous figures describe the calculated dynamic load and its frequency spectrum when the train speed is 50 km/h, which clearly show that the force is mainly induced by the moving axle loads of vehicles, and that the load mainly concentrates at the frequency range of 0 to 10Hz. This load is adopted as the dynamic load for the next calculation.
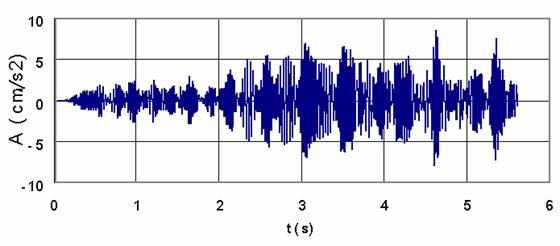
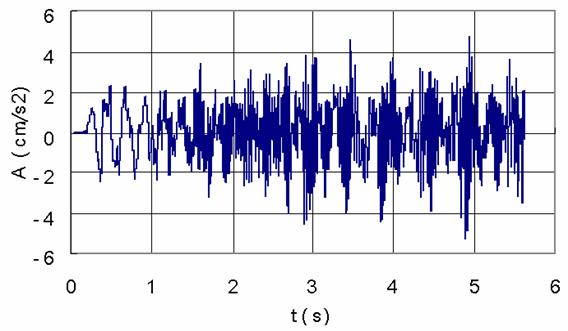
Figure 7 shows the distribution of ground vibrations at two locations perpendicular to the tunnel centreline. It can be seen that the maximum acceleration within the distance of 30m (4.9cm/s2) is smaller than the maximum level at 0 m (8.1cm/s2). The difference between computed acceleration time histories computed at these locations is due to the vibration attenuation with distance. This attenuation of the peak acceleration from 8.1 to 4.9 might be dependent on the train speed and train loading, the geotechnical conditions of the soil and possibly to the frequency components of the train-track excitation loading that is filtered throughout soil layers.
|
a) at 0 m from the tunnel centreline
b) at 30 m from the tunnel centreline |
|
Figure 7. Ground acceleration time histories |
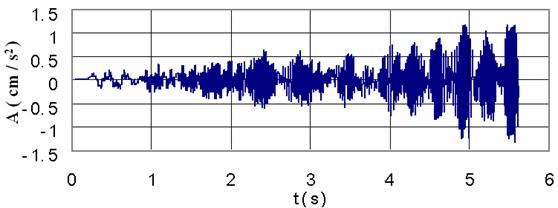
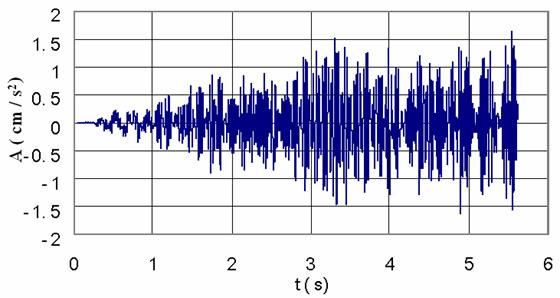
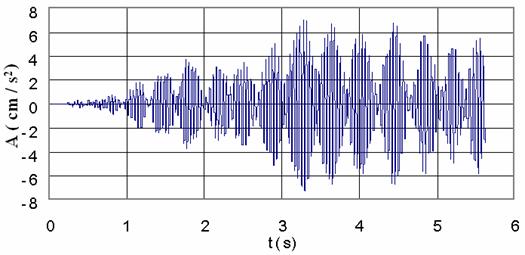
The train still running at the speed of 50km/h, the building acceleration time-histories of the first floor, the 8th floor and the top floor are illustrated in figure 8. It can be seen that the form of acceleration amplitude changes at different floor. With the present vibration amplification of the maximal acceleration response from the first floor to the top floor level, it is obvious that the building structure generates energy with time increment, what is easily noticed at the first floor level in figure 8a.
|
a) at the first floor |
|
b) at the 8-th floor |
|
Figure 8. The acceleration time history at different floor levels |
|
c) at the top level |
|
Figure 8. The acceleration time history at different floor levels |
Many investigations support that in a structure under specific modal vibration, some of its parts or elements can be subjected to local resonance and even self-excitation. Thus the observed acceleration amplification from the 3-rd second in figure 8.c is related to local resonance. From literature survey [16-17, 23-26] it is known that there are no damages on a building due to train induced ground-borne vibration even if human occupants of the buildings might be seriously affected. But the computed results from the given model shows that there is the possibility for an underground train, passing through an urban area under specific sub-models described above, to excite a particular building or some of its elements with one of their natural frequencies, thus creating the resonance problem. Investigations on this problem are still going on in the Department.
Conclusions
The TSS presented in this paper is subdivided into three main sub-models: the source, the propagation path and the receiver in order to study and understand the influence of factors such as dynamic characteristics of the train, the railway structure, soil and building characteristics, on ground-born vibrations and their effects on nearby building structures.
By dividing the TSS model into sub-models it is possible to replace some parts of the model with data from a particular site if available. Thus, if a new railway is being designed close to a building, a prediction with good accuracy can be made on the effects of the anticipated railway on the building.
With the limitations of available data on TSS interaction in Cameroon, experiments and measurements are still to be done at sites with different geotechnical conditions, different train-track models and different building types to validate obtained results, and thus elucidate these important facts.
Acknowledgements
This paper is a continuation of the study presented at the “3rd International Symposium on Environmental Vibrations: Prediction, Monitoring, Mitigation and Evaluation”, 2007.
References
1. The World Bank, Cameroon, Upgrading Low Income Urban Settlements - Country Assessment Report, 2002, AFTU 1 & 2. Available at: http://web.mit.edu/urbanupgrading/upgrading/case-examples/overview-africa/country-assessments/download/CAMEROON.pdf, (accessed 08/06/2013).
2. NRMP, The National Railway Network Master Plan in Cameroon, Final report of the prefeasibility study conducted by KORPEC (KORea Port Engineering Corporation) and Validated by the Government of Cameroon, 2012, p. 390-402.
3. Du X.T., Xu Y. L., Xia H., Dynamic interaction of bridge–train system under non-uniform seismic ground motion, Earthquake Engineering Structural Dynamics, 2012, 41, p. 139-157, DOI: 10.1002/eqe.1122
4. Rodríguez-Tembleque L., Abascal R., A 3D FEM–BEM Rolling Contact Formulation for Unstructured Meshes, International Journal of Solids and Structures, 2010, 47, p. 330-353, Available at: http://www.sciencedirect.com/science/article/pii/S0020768309003953, (accessed 08/06/2013).
5. Zolghadr Jahromi H., Izzuddin B.A., Zdravkovic L., Partitioned analysis of nonlinear soil-structure interaction using iterative coupling, Interaction and Multiscale Mechanics, 2007, 1(1), p. 33-51.
6. Xia H., Dynamic Interaction of Vehicles and Structures, Science Press., Beijing, China, 2002.
7. Chore H.S., Ingle R.K., Sawant V.A., Building frame - pile foundation - soil interaction analysis: a parametric study, Interaction and Multiscale Mechanics, 2010, 3(1), p. 55-79.
8. Krylov V.V., Effects of track properties on ground vibrations generated by high-speed trains, ACUSTICA-Acta Acustica, 1998, 84(1), p. 78-90.
9. Daumueller A.N., Jauregui D.V., Strain-Based Evaluation of a Steel Through-Girder Railroad Bridge, Hindawi Publishing Corporation, Advances in Civil Engineering, 2012, Available at: http://www.hindawi.com/journals/amse/ai/,(accessed 17/06/2013)
10. Xiaoyan L., Numerical Analysis of Track Structures in Railway, Beijing, China Railway Press, 1998
11. Grassie S.L., Gregory R.W., Dynamic response of railway track to high frequency vertical excitation, Journal of Mechanical Engineering Science, 1982, 24(2), p. 77-90.
12. Flýba L., Vibration of Solids and Structures Under Moving Loads, London, Thomas Telford, 1999.
13. Weitsman Y., On foundations that react in compression only, Journal of Applied Mechanics, 1970, 12, p. 1019-1030.
14. Wang K., Liu P., Lateral Stability Analysis of Heavy-Haul Vehicle on Curved Track Based on Wheel/Rail Coupled Dynamics, Journal of Transportation Technologies, 2012, 2(2), p. 150-157, Available at: http://www.SciRP.org/journal/jtts, (accessed 08/06/2013)
15. Woods R.D., Screening of Surface Waves in Soils, Journal of Soil Mechanics and Foundation Division, Proceedings of the ASCE, 1968.
16. Woods R.D., Larry P.J., Energy-Attenuation Relationships from Construction Vibrations, Vibration Problems in Geotechnical Engineering, ASCE Proceedings, Detroit, Michigan, 1985.
17. Eisenman J., Deischl F., Structure-Borne Sound from Underground Railway Systems, Der Eisenbahningenieur, 1986, 3, p. 101-110.
18. Alshawi M., Underwood J., Improving the constructability of design solutions through an integrated system, Journal of Engineering, Construction and Architectural Management, 1993, 3(1&2), p. 47–67, doi:10.1108/eb021022.
19. Patrick C., Low Vibration and Noise Track Systems with Tunable Properties for Modern LRT/Streetcar Track on Surface in Urban Areas, TIVC’2001, International Symposium on Traffic Induced Vibrations & Controls. Beijing, China, 2001, p. 161-176.
20. Xia H., Cao Y.M., Zhang N., Numerical Analysis of Vibration Effects of Metro Trains on Surrounding Environment,. Int. J. of Structural Stability and Dynamics, 2007, 7, p. 45-56.
21. Le Kouby A., Bourgeois E., Rocher-Lacoste F., Subgrade Improvement Method for Existing Railway Lines – an Experimental and Numerical Study, Electronic Journal of Geotechnical Engineering, 2010, 15, p.461-494.
22. Di Mino G., Di Liberto C.M., Nigrelli J., A FEM model of rail track-ground system to calculate the ground borne vibrations: a case of rail track with wooden sleepers and k-fastenings at Castelvetrano, Advanced Characterisation of Pavement and Soil Engineering Materials, Athens, Greece, 2007, p. 1737-1752.
23. Chauhan H.M., Pomal M.M, Bhuta G.N., A Comparative Study Of Wind Forces On High-Rise Buildings as Per Is 875-Iii (1987) and Proposed Draft Code (2011), GRA - Global Research Analysis, 2013, 2(5), p. 59-60.
24. Lei X., Zhang B., Influence of track stiffness distribution on vehicle and track interactions in track transition, Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2010, 224:592, p. 592-604, Available at: http://pif.sagepub.com/content/224/6/592 (accessed 28/08/2012).
25. Thorat Y.V., Kadam S.S., Design and Development of Test Setup for VibrationAnalysis with Soft Foot, Indian Journal of Applied Research, 2012, 2(3), p. 59-62.
26. Xiaojing Sun, Weining Liu, Dawen Xie, Yingxuan Jia, Vibration impacts on adjacent sensitive buildings induced by metro trains, World Tunnel Congress 2008 - Underground Facilities for Better Environment and Safety – India, Agra, 2008, p. 1382-1389.