Effect of the Degree of Plastic Deformation on the Electrical Resistance and Thermal Conductivity of Al-Mg-Si Alloy

Joseph Ajibade OMOTOYINBO, Isiaka Oluwole OLADELE and Wasiu SHOKOYA

Department of Metallurgical and Materials Engineering, Federal University of Technology, Akure, Nigeria.

E-mails: ajibadeomotoyinbo@yahoo.com; wolesuccess2000@yahoo.com

Corresponding Author: Phone: +2348035927598

Abstract

Experiments have been conducted to investigate the effect of the degree of plastic deformation on the electrical resistance and thermal conductivity of Al-Mg-Si (6063) alloy. Thirty six samples of the 6063 alloy were used in all for the experiments (three samples constituted a group and twelve groups were instituted in the experiment with each group corresponding to a particular degree of deformation). Eleven groups were cold deformed plastically by subjecting the groups to different percentages of cold work starting from 5% to 55%, with 5% intervals. It was observed that there was no appreciable increase in the electrical resistance of the alloy as the degree of deformation increased. However, cold deformed 6063-Aluminium alloy appeared to be thermally unstable as the degree of plastic deformation increased. It was concluded that plastic deformation has no deleterious effect on the electrical resistance of the alloy but rendered the material thermally unstable in terms of thermal conductivity.

Keywords

Plastic Deformation; Electrical Resistance; Thermal Conductivity.

Introduction

Metals, in the solid state, have a crystalline structure and the crystals or grains are made up of particles arranged in strict geometric patterns called space lattices. Due to the strict geometry of the space lattices, plastic deformation can occur in solid state [1].

When plastic deformation occurs during hot or cold working, planes of atoms slip past each other, bringing about a change in the relative orientation and position of the atoms thus affecting the electric potential [2]. Usually, slip planes lies between and are parallel to the planes of greatest atomic density [3]. It is long established that when a ductile or malleable crystalline material such as Aluminium alloy is subjected to an applied force of sufficient magnitude, movement of the lattice structure can occur along slip planes thereby altering the physical and mechanical properties of the alloy in accordance with the processing-structure- property relationship in materials [4].

Like other metals, the properties of Aluminium such as electrical and thermal conductivity are affected by plastic deformation [5-6]. Cold working, a form of plastic deformation (shaping) process mostly used in producing electrical cables has a deleterious effect on thermal and electrical properties of metals and must therefore, be modified or controlled effectively so as to nullify the undesirable effects. Cold working usually distorts the whole crystal lattice and makes it more difficult for electron flow to occur [7]. Furthermore, alloying elements like magnesium and silicon also reduce the electrical conductivity of aluminium alloys [1]. Aluminium is a good conductor of electricity and heat because of the large number of free electrons moving about its lattice structure [8]. Similarly, [9] remarked that strengthening of light and very ductile metals such as aluminium can be achieved by strain hardening through cold working in order to withstand service conditions, but conductors strengthened in this way may tend to exhibit poor thermal stability and show susceptibility to mechanical failure. Though, process annealing of the cold worked alloy is usually put in place in the industrial production of electric cables, there is need to critically monitor and control the mode and degree of plastic deformation in order for the alloy to exhibit optimum conductivity values.

A study by [10] show the effect of cold working on 6063 aluminium alloy and remarked that significant effects on mechanical and electrical properties abound. Precisely, substantial improvement on toughness, strength, and hardness is noticed, while low resistance to current flow was reported feasible at a thickness reduction in the neighbourhood of 5%, and impairment of conductivity is envisaged under severe plastic deformation but no attempt was made to carry out such deformation.

The effect of artificial ageing on plane anisotropy of 6063 aluminium alloy was also worked upon by [11] and affirmed that moderate thermal treatment improved the formability and fracture toughness of the alloy with minimal anisotropy without correlating such effect with electrical resistance or conductivity.

In this work, the influence of a specific mode of plastic working on the electrical resistance and thermal conductivity of 6063-Aluminium alloy was investigated. This is important because the alloy is employed as electric cables in many countries, for instance, in Nigeria.

Material and Method

Aluminium-Magnesium-Silicon (6063) alloy obtained from Nigerian Aluminium Extrusion Company (NIGALEX), Lagos was used for the study. The composition of the alloy obtained from spark spectrometric analysis is given in Table 1 below,

Table 1. Chemical Composition of the 6063 alloy (wt %)

Elements	Si	Fe	Mn	Mg	Cr	Ti	Ca	Al
% Chemical Composition	0.455	0.201	0.023	0.487	0.002	0.001	0.012	Balance

The hot extruded, unaged, 6063 Aluminium alloy rod, (30 mm diameter and 600 mm length) obtained from NIGALEX is shown in Figure 1.

Figure 1. Extruded Al-Mg-Si alloy

Thirty-six (36) pieces, of 12 mm thickness and 30 mm diameter test specimens (or samples) were machined out of this stock using a power hacksaw. The test specimens are in form of small discs.

The thirty-six discs were then divided into twelve groups, each group consisting of three specimens. Group 2 specimens were deformed by 5%, group 3 deformed by 10%, group 4 by 15%, group 5 by 20%, group 6 by 25%, group 7 by 30%, group 8 by 35%, group 9 by 40%, group 10 by 45%, group11 by 50% and group 12 by 55%. The above arrangement constitutes three (3) runs for each percentage deformation. Average values were then recorded.

Electrical Resistance Test: The experiments used to determine the electrical resistance of the cold rolled specimens is the standard Ohm’s experiment. The set-up is as represented in the circuit diagram below.

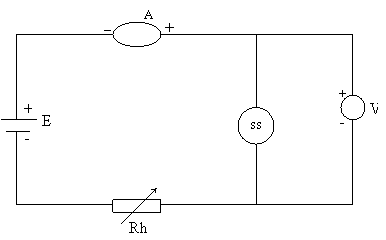
Figure 2. Circuit Diagram of Ohm’s Experiment

A 5 volts (DC) electrical power was supplied through the entire set up. The current and voltage or potential difference (p.d) across the specimens for 1, 2, 3, 4 and 5 minutes were read from the ammeter and voltmeter respectively and recorded. Average values were again computed and recorded.

Theory: The resistance (R) of the specimen to the flow of electricity is calculated from ohm’s law making use of the equation

R=V/I

(1)

where R is in Ohms (Ω), V is Voltage passing through the specimen; I is the current (in amperes) passing through the sample.

Resistivity is calculated from the expression,

ρ= RA/L

(2)

where ρ is resistivity in Ohm’s m (Ωm); R is resistance of the specimen to the flow of electricity; A is the area of the specimen in m², and L is the length of the specimen in m.

The electrical conductivity (σ) which is the inverse of resistivity is also given as

σ = 1/ρ

(3)

Results of electrical properties of the worked alloy are presented in figure 4, 5, and 6.

Thermal Conductivity Test: Thermal conductivity test was performed on the specimens (or samples) using the Lee’s Disc method, the details of which can be found in literature [8], T  The Lee’s Disc Apparatus (Figure 3) is made of polish wood and it consists of disc A, B, C, heater disc, and a space for the sample to be inserted to determine its thermal conductivity. There is a hole on each disc inside which the thermometer is placed. The discs A, B and C are of the same diameter and thickness, while the heater disc is of the same diameter but with a smaller thickness.

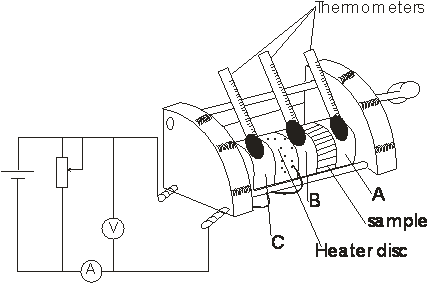
Figure 3. The Lee’s thermal Conductivity Experiment Set-up [12]

The disc and the samples were wiped and cleansed of dirts and placed in the order shown in Figure 3. It was ensured that the thermometer holes face upwards vertically and the clamp screw was tightened to hold it firmly. In order to avoid breakage of the thermometer, a small amount of glycerine was poured in each thermometer hole.

The heater disc was connected to a 6 V power supply as shown in Figure 3, and the fourth thermometer was placed fairly closed to the apparatus to measure the ambient temperature. The thermometer reading was allowed to be steady for 5 minutes before the initial reading of each of the four thermometers were taken. The final reading in each case was taken after 20 minutes of taking the initial reading. The same procedure was repeated for the entire samples.

Theory and Calculations: The following assumptions are made:

1. The heat transferred between the object and the surrounding depends on the exposed surface area of the object and temperature difference between the object and the surroundings.

2. Energy E (heat flux) is emitted from each exposed unit area of surface per seconds per °C above ambient temperature. E is measured in Js^-1m^-2 °C^-1.

3. This energy is the same for all the discs, and the temperature of the samples is the   mean temperature of A,B and C , hence the total heat emitted from the apparatus H, is

(4)

where α_A,α_B,α_C, and α_S are exposed surface areas on m² of A,B,C and S respectively (area α_A,α_B,α_C include the flat and sections of disc). T_A, T_B, T_c is the temperatures of the discs A, B, and C at steady state above the initial temperature respectively. The heat is supplied by the heating element (disc).

H=VI Js^-1

(5)

Where V is potential difference across the element (in volts) and I is the current flowing in amperes. From equation 4 and 5

	(6)
	(7)

From heat conduction equation i.e. Fourier law, the heat flowing through sample S, equals that of disc C. Hence the heat flowing through the sample is given as

hs = kA                or         hs = kA Js^-1

(8)

For a cylindrical (disc) specimen(s) A = area= Πr²

hs = kΠr^2    Js^-1

(9)

where r = radius of sample/specimen (s)

 k= thermal conductivity of sample

 d= thickness of sample.

All the heat entering S from B does not pass into A as some will be emitted from the curved surface of S. Assuming that the heat flow through S is the mean of the heat entering S from B is that which is emitted by S and A together. Hence, the heat entering S

from B is equal to heat emitted by S and;

hBS=

(10)

Also the heat leaving S and A is equal to heat emitted by A;

hSA = EαsTA  Js^-1

(11)

The mean of equation 10 and 11 is taken as

hs = Js^-1

(12)

From equation 9 and 12 we have

kΠr^2 =

(13)

Therefore,

k=              Js^-1m^-1 oC^-1

(14)

where k is the thermal conductivity of the samples.

Results and Discussion

The results obtained in this investigation are presented in Figures 4-10. Both electrical and thermal properties are crucial in materials application and these characteristics are affected by processing techniques consequent upon the processing-structure-property relationship in materials [13].

Effect of Plastic Deformation on Electrical Resistance and Conductivity: Electrical resistance is the most important tool in determining both electrical resistivity and conductivity of a material as shown in Figures 4, 5 and 6. It is seen in Figure 5 that the curves for the variation of resistance and resistivity with percentage deformation show a remarkable resemblance. Consequently, a rise in resistance brings about a rise in resistivity. On the contrary, the increase in resistance and resistivity culminates in a decrease in electrical conductivity. The reason for the initial decrease in resistance and resistivity of the alloy at lower degrees of deformation (1%-5%)and no deformation(as received) state could be adduced to the relatively low level of dislocations compared to what obtains at higher degrees of deformation. At lower degrees of deformation, electron scattering by dislocations is low resulting into low resistance to the flow of current. Furthermore, at very low degree of deformation, there are few second phase (Mg₂Si) particles and this equally, favours reduced resistance to current flow. The microstructure of the alloy at this level of deformation shows no evidence of mechanical fiberings, which are potential sites for dislocations, (Figure 11).

At 10% deformation (Figure 5) a rise in resistance and resistivity is readily observed due to the increase in dislocation density, as well as, the number of coarse, poorly conducting precipitates of Mg₂Si phase scattered at grain boundaries of the alloy.

At higher percentages of deformation above 10%, there is fluctuation in the manner of change of resistance and resistivity. This situation points to the fact that not only electron-scattering dislocations and second phase (Mg₂Si) particles might be responsible for the lowering or otherwise of resistance. Others factors such as closing up of voids, generation of cracks due to localized stress concentration, annihilation of dislocations, and small rise in temperature of the specimens during plastic deformation may contribute immensely to the level of resistance to the flow of current in the Al-Mg-Si alloy. It is a well-established fact that temperature rise inhibits the flow of current [14]. The points with highest resistance (20% and 40% deformation) show evidently clusters of lines (cracks) which prevent easy assage of current (Figure 12).

The overall effect of increasing degree of plastic deformation on the electrical conductivity of Al-Mg-Si alloy as revealed in this study (Figure 6) is that conductivity tends to increase with increasing degree of deformation. In other words, work hardening is less deleterious on the electrical conductivity of Al-Mg-Si alloy than may be expected. It is likely that some dislocations annihilation do take place as the degree of plastic deformation increases, thereby reducing the numbers of electron-scattering dislocations which in turn lowers the electrical resistivity of the deformed alloy.

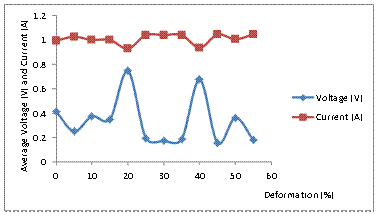
Figure 4. Variation of Voltage and Current passing through the Sample with

Percentage Deformation

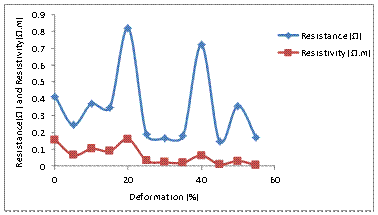
Figure 5. Variation of Electrical Resistance and Resistivity passing through the Sample with Percentage Deformation

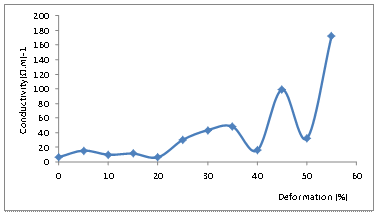
Figure 6. Variation of Electrical Conductivity passing through the Sample with Percentage Deformation

Usually, plastic deformation raises the electrical resistivity of alloys because of increased numbers of electron-scattering dislocations, which in turn lowers the electrical conductivity. But where the numbers of electron–scattering dislocations are reduced by virtue of dislocation annihilation, the electrical resistivity may not be raised appreciably leading to enhanced conductivity. According to [15] methods used to strengthen metals and alloys generally cause a pronounced decrease in electrical conductivity, so that trade-off must be made between conductivity and strengthening for specific applications.

Effect of Plastic Deformation on Thermal Conductivity: Figures 7 to 10 reflect the variation of the measured thermal properties of the alloy with percentage deformation. Figure 7 shows the plot of the computed thermal energy E, emitted by the standard discs of the thermal conductivity apparatus against the percentage deformation of the absorbing deformed alloy discs. From the figure, it could observed globally that there is a slight increase in the amount of energy E, emitted by the standard discs with increasing percentage deformation of the absorbing, deformed alloy discs.

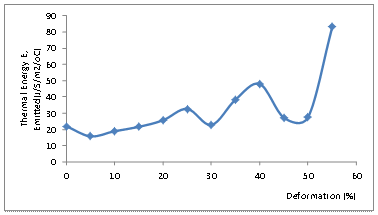
Figure 7. Variation of Thermal Energy E, Emitted with Percentage Deformation

Figure 8 presents the variation of the total heat emitted H, from the Lee’s apparatus as a function of the degree of deformation of the studied samples. The curve reflects a situation of heat instability. This is an indication to the fact that due to the large amount of cold working, the samples become thermally unstable and the rate of heat emission is enhanced. The closer packing of atoms consequent upon plastic deformation which apparently no longer give room for discontinuities and hiding place for the heat absorbed, is thought to account for the instability; and since the alloy Al-Mg-Si is ordinarily, a good conductor of heat and conduction is enhanced by physical or in this case atomic contact between conducting atoms,

the absorbed heat is quickly transferred from one atom to the other and then radiated away [16-17].

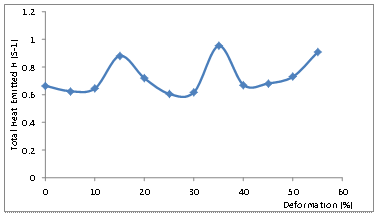
Figure 8. Variation of Total Heat Emitted, H with Percentage Deformation

It was also observed that as the degree of deformation increases, the rate of increase in temperature of the samples increased despite the equal rate of the heating of the specimens. This is due to the closing up of voids within the alloy, thereby increasing the contact area within the α-phase matrix by virtue of plastic deformation.

For ductile metals such as Al-Mg-Si alloy, alleviation of thermally induced stress may be accomplished by plastic deformation; this in turn would lead to improved heat conductivity [18-19]. Figures 9 and 10 reveal clearly that increasing the degree of plastic deformation on the average leads to enhanced thermal conductivity, as a result of improved electronic conduction.

However, in case of the presence of substantial level of crystalline imperfections (e.g. vacancies, interstitial atoms, and dislocations) a fairly unstable situation may arise [10, 20].

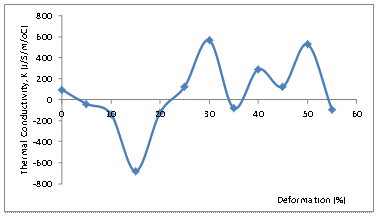
Figure 9. Variation of Thermal Conductivity, K with Percentage Deformation

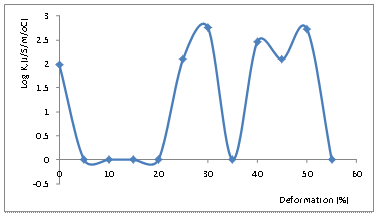
Figure 10. Variation of Log K with Percentage Deformation

Figure 11. Typical microstructure of the 6063 alloy in as-received state showing particles of Fe₃SiAl₁₂ (scriptlike), and Mg₂Si (small blocky form) in a matrix of Aluminium rich  solid solution. No evidence of mechanical fibering. Etched in 0.5 percent HF, 250x

Figure 12.Typical microstructure of the 6063 alloy subjected to 40% degree of deformation showing particles of Fe₃SiAl₁₂ (scriptlike), and Mg₂Si (small blocky form) in a matrix of Aluminium rich solid solution. Mechanical fibering is evident. Etched in 0.5 percent HF, 250x

Conclusions

From the results obtained in this study the following conclusions are drawn:

· Plastic deformation raises the electrical resistivity of Al-Mg-Si alloy where there are large numbers of electron-scattering dislocations and lowers the resistivity of the alloy in the presence of few electron-scattering dislocations.

· Other factors such as closing up of voids, generation of cracks due to localized stress concentration, annihilation of dislocations, and small rise in temperature during plastic deformation also contribute immensely to the level of resistance to the flow of current in the Al-Mg-Si alloy.

· Plastic deformation increased the rate of emission of heat from the alloy due to closing up of voids, which makes it more thermally conducting by virtue of improved atomic contact within the alloy matrix.

· A cold work alloy becomes thermally unstable, as it cannot retain much heat within itself; therefore, it is not advisable to strengthen metals that are to be used as heating elements by cold working.

Reference

1. Timings R.L., Engineering Materials, 1989, 1, p.8-264.

2. Bube R.H., Electrons in Solids, Third edition, 1992, Academic Press, San Diego.

3. Hummel R.E., Electronic Properties of Materials, Second edition, Springer-Verlag New York Inc., New York. 1992.

4. Chaudhari P., Electronic and Magnetic Materials, Scientific American, 1986, 255(4), p. 136-144.

5. Higgins R.A., Properties of Engineering Materials, ELBS, Great Britain, 1985, p. 367-371.

6. Sungho Jin., Recent Advances in Electrically Conductive Materials. Journal of Minerals, Metals and Materials (JOM), USA, 1997, 49(3), p 37.

7. Incropera F.P. , Fundamentals of Heat and Mass Transfer, Second edition, John Wiley and Sons Inc., Singapore, 1985, p. 2-6.

8. Holman J.P., Heat Transfer, Seventh edition, McGraw-Hill Book Company Singapore, 1990, p.1-20.

9. Polmear I.J., Light Alloys, Metallurgy of the Light Metals, Second edition, Edward Arnold Limited, London, 1993, p.1-167.

10. Adeosun S.O., Sekunowo O.I., Balogun S.A., Osoba L.O. Effect of Deformation on the Mechanical and Electrical Properties of Aluminum-Magnesium Alloy. Journal of Minerals and Materials Characterization and Engineering, 2011, 10(6), p.553-560.

11. Adeosun S.O., Sekunowo O.I., Bodude M.A., Agbeleye A.A., Balogun S.A., and Onovo H.O. Effect of Artificial Aging on Plane Anisotropy of 6063 Aluminium Alloy. International Scholarly Research Network ISRN Metallurgy, 2012, p. 5.

12. Federal University of Technology Akure, Physics Electronic Laboratory, 2012.

13. Heringhaus F., Schneider-Muntau H.J., Gottenstein G., Analytical Modelling of Electrical Conductivity of metal matrix composites-Bulk Scattering Mechanism in Metals. Materials Science and Engineering A, 2003, 347(1-2), p. 9-20.

14. Bowler N., and Huang Y. Electrical Conductivity Measurement of Metal Plates using Broadband Eddy-Current and Four-Point. Journal of Measurement Science Technology, 2005, 16(11), p. 2193-2200.

15. Lu L., Shen X., Qian L., Lu K. Ultrahigh Strength and High Electrical Conductivity in Copper Alloys. Science, 2004, 304(5669), p. 442-426.

16. Bolt P.J., Lamboo N.A.P.M., Rozier P.J.C.M. Feasibility of warm drawing of Aluminium products. Journal of Materials Processing Technology, 2001, 115(1), p.118-121.

17. Riahifar R. and Serajzadeh S. Three Dimensional Model for Hot rolling of Aluminium Alloys - Thermal Conductivity of 6063 Aluminium Alloy. Material and Design, 2007, 28(8), p. 2366-2372.

18. Kamat R.G., Butler J.F., Murtha S.J., Bovard F.S., Alloy 6022-T4E29 for automotive sheet applications. Mater. Sci. Forum, 2002, 396, p. 1591-1596.

19. Panigrahi S.K., and Jayaganthan R. Effect of Rolling Temperature on Microstructure and Mechanical Properties of 6063 Aluminium Alloy- Thermal Behaviour of Samples. Materials Science and Engineering A, 2008, 492(1-2), p. 300-305.

20. Bournane M., Berezina A.,Davydenko O., Monastyrska T., Molebny O., Spuskanyuk A., Kotko A., Effect of Severe Plastic Deformation on Structure and Properties of Al-Mg-Si Alloy of 6060 Type. Materials Science and Metallurgy Engineering, 2013, 1(2), p.13-21.