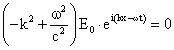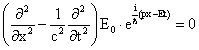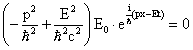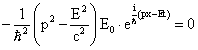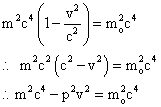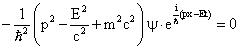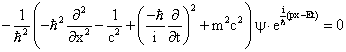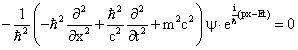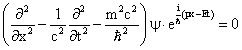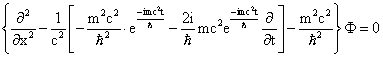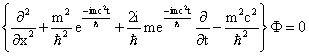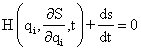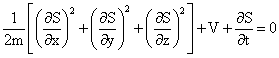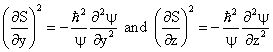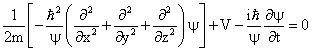Deriving time dependent Schrödinger equation from Wave-Mechanics, Schrödinger time independent equation, Classical and Hamilton-Jacobi equations

Nilesh P. BARDE^1*, Sandeep D. PATIL², Pravin M. KOKNE¹, Pranav P. BARDAPURKAR³

¹Department of Physics, Badrinarayan Barwale Mahavidyalaya, Jalna, Maharashtra, India

²Department of Mathematics, Badrinarayan Barwale Mahavidyalaya, Jalna, Maharashtra, India

³Department of Physics, S. N. Arts, D.J. Malpani Commerce & B. N. Sarda Science College, Sangamner, Maharashtra, India

E-mails: *nilesh_barde123@rediffmail.com; patil2005@rediffmail.com; pravin.kokne@rediffmail.com; bardapurkar@gmail.com

*Corresponding author, phone: +919420808535

Abstract

The concept of time dependent Schrödinger equation (TDSE) illustrated in literature and even during class room teaching is mostly either complex or meant for advanced learners. This article is intended to enlighten the concept to the beginners in the field and further to improve knowledge about detailed steps for abstract mathematical formulation used which helps in understanding to derive TDSE using various tools and in more comprehensible manner. It is shown that TDSE may be derived using wave mechanics, time independent equation, classical & Hamilton-Jacobi’s equations. Similar attempts have been done earlier by some researchers. However, this article provides a comprehensive, lucid and well derived derivation, derived using various approaches, which would make this article unique.

Keywords

Schrödinger wave equation; Simple harmonic motion; Hamilton-Jacobi’s equation

Introduction

Quantum Mechanics is an essential part of undergraduate syllabus in Physics as well as in Chemistry. This specialized branch of physics mainly deals with subatomic particles and the era where Newtonian laws are not obeyed.

While a student is uplifted from higher secondary level to graduate classes, he has a high impact and firm belief in classical mechanics and Newtonian laws. Many terms in quantum mechanics are contradictory to their classical counterparts. This underlines the importance and need of a focussed a ‘step-down’ approach to teach the new notions. The most crucial part of quantum mechanics comes when a teacher has to deal with what is called “Schrödinger’s equations (SE)” and the most regretful saga is that in most of the cases, this is dealt as a black box and hardly any efforts are taken to derive them following the “known to unknown” path.

In fact, it is expected that a teacher should start from the familiar concepts in classical mechanics and should land down with derivation of these equations giving the physical significance meaningfully. Same is the approach followed in many of the standard books. Many researchers, educationalists have attempted to bridge this gap and tried to give derivations of SE starting from many fundamental principles. However, again many of such attempts are thorny for undergraduate students. [1-9]

This pitfall itself is the motivation for the present work. Although similar attempts have been done by many researchers, this article has a primitive thrust to provide the derivation of SE giving detailed description with deduction of every small step involved in deriving it. Further, it is intended that the reader should get introduced with a variety of ways to derive the SE, with a least prerequisite knowledge of quantum mechanics.

This article provides the simplified derivation of Time Dependent Schrödinger’s Equation starting from wave mechanics, Schrödinger Time Independent Equation, classical and Hamilton-Jacobi equations.

On Schrödinger’s equation

In1924, de-Broglie suggested that every moving particle has a wave associated with it, which is also known as matter wave. Further, Erwin Schrödinger in continuation to de-Broglie’s hypothesis introduced a differential wave equation of second order to explain the wave nature of matter and particle associated to wave. This equation is analogous to the equation for waves in optics, which assumes that the particle behaves as wave and yields solution in terms of a function called the wave function. When this equation is solved, it gives two things; namely the wave function Ψ and the energy E, of the particle under consideration. Once the wave function Ψ is known, then everything about the particle is known or can be deduced from the wave function. Thus, the wave function Ψ is the most important thing, which itself does not have any physical significance, however the absolute square of Ψ, i.e. |Ψ|² gives the probability of finding the particle in a particular region of space at a particular instant of time. The term E in the equation is the energy of the particle depending upon the potential V and boundary conditions (constraints on the particle) can be continuous or quantized. Quantization of energy of the particle is a remarkable feature of the quantum mechanics i.e. a particle cannot have any energy or continuous energy, but can have only that permitted energy described by Schrödinger equation together with the potential V and the boundary conditions [10, 11].

Schrödinger’s equation was very much popular, though initially it was questioned by scientific community due to its limitation regarding non-relativistic particles. Heisenberg developed a matrix mechanics in which physical quantities are explained in terms of Eigen values of the matrix [6]. The mathematical equations in equivalence to matrix mechanics were successfully shown by Schrödinger in the series of papers published in 1926; the theory later on was consequently called as wave mechanics. Heisenberg’s matrix mechanics and Schrödinger’s wave mechanics were known to be two different descriptions of quantum mechanics [10-16].

Basically Schrödinger equations have two forms: one consisting of time termed as time dependent equation and the other in which time factor is eliminated and hence named as time independent equation [17-21].

Material and method

Different methods used to derive TDSE:

a) Using wave mechanics

Propagation of a wave makes particles of the medium to oscillate about their mean position. These oscillations are ‘to and fro, along the same path’ and the motion is referred as Simple Harmonic Motion (S.H.M.). Displacement of a particle from its mean position is given by a simple equation from wave mechanics, as

which can further be modified to

Quantum mechanically, this particle, describing S.H.M. in accordance with equation (0-II) has a wave, or in particular - a matter wave, associated with it, which is represented by a wave function y(x,t). This wave function is not a directly measurable quantity and may be complex in nature. The wave function associated with a particle moving along +x direction is given by

(1)

where, A is the amplitude of oscillations, ω is angular frequency, t is the time, x is position and v is its velocity.

As ω = 2πν and v = νλ, equation (1) modifies to,

(2)

If n is the frequency of oscillations, the total energy is given by

(3)

where ‘h’ is Planck’s constant and

Thus,

Also,  (by de-Broglie’s hypothesis)

Therefore equation (2) becomes

	(4)

Equation (4) represents a mathematical representation of an unrestricted particle of total energy E and momentum p moving along +x direction.

The total energy (E) of the particle can be written as

T.E. = E = K.E. + P.E.
	(5)

where, V is potential energy of the particle which is a function of x.

Differentiating equation (4) w.r. to x,

(6)

Again differentiating with respect to x,

Using equation (4),

(7)

which then becomes

(8)

Differentiating equation (4) with respect to t,

(9)

Again using equation (4),

	(10)
	(11)

Equation (5) becomes,

(12)

Substituting equations (8) and (11) in equation (5),

(13)

Equation (13) is the one dimensional TDSE. The same can be written in three dimensions as

(14)

where  is a Laplacian operator.

Thus, the Time Dependent Schrödinger Equation, TDSE, can be derived from the wave mechanics considering the equations for a particle describing S.H.M. This derivation has its own importance as it paves the way from classical to quantum mechanics.

Using Schrödinger’s time independent equation

The Schrödinger’s time independent equation in 3-D is given by,

(15)

Consider, a wave function represented as:

Ψ = A∙e^-iωt

(16)

where, A is amplitude of the wave, ω is an angular frequency and t is the time period. Differentiating equation (16) w.r. to t,

(17)

i.e., as E = hν

(18)

Hence, equation (15) becomes,

	(19)
	(20)

The above equation represents TDSE with the term:

 as the Hamiltonian operator.

Thus, the two legendary equations have a fair connection. These two equations are like statics and dynamics in classical mechanics, hence, derivability of the time dependent equation from the time independent form is much significant.

Using classical wave equation

The 1-D equation for an electromagnetic wave is expressed as

(21)

where, E is the energy of the wave, c is the velocity of light and t is the time, for a wave propagating in x-direction. The above equation is derived from Maxwell’s equations which governs EM waves in electrodynamics [9]. The solution is a plane wave solution which satisfies the above equation represented as

E(x, t) = E0∙e^i(kx-ωt)

(22)

where, k is propagation constant and ω is an angular frequency. Differentiating equation (22) w.r.to x,

(23)

Again differentiating w.r.to x,

(24)

Differentiating equation (22) w.r.to t,

(25)

Again differentiating w.r.to t,

(26)

Equation (21) becomes,

(27)

As, c = nl

(28)

Equation (22) becomes,

(29)

Differentiating equation (29) w.r.to x,

(30)

Differentiating again w.r.to x,

(31)

Differentiating equation (29) w.r.to t,

(32)

Differentiating again w.r.to t,

Equation (21) becomes,

E2 = p2c2	(33)

_{Now, the relativistic mass of a particle with rest mass mo, is given by}

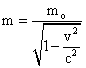
_{which can further be written as}

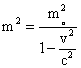
_{Multiplying the above equation by ,}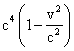

	(34)

_{Thus for an EM wave, considering E = mc2, equation (34) takes the form-}

(35)

_{Equation (33) refers to energy in case of non relativistic considerations. However, when the relativistic effects are considered, the same expression (equation – 33) modifies to equation (35). The rest mass term ‘mo’ will further be used as ‘m’ for the sake of simplicity.}

_{Thus, from equation (35),}

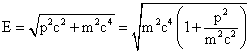
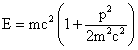
where, the higher order terms are neglected.

(36)

where, T is the classical kinetic energy.

            As we are not dealing with any electric field, the energy term in equation (29) may be replaced by any wave function Ψ and is represented by,

(37)

where, is amplitude of the wave.

The total energy from equation (36) can be substituted in equation (37) which leads to

	(38)

The first term of equation (38), , is associated with velocity of light, ‘c’, whereas the later term i.e. is associated with velocity of the particle. As the particle velocity can never be greater than that of the light, it is obvious that the former term will oscillate faster than the later.

Now, equation (38) can be written as

(39)

where, _{and is a non-relativistic function.}

Differentiating equation (39) twice with respect to ‘t’,

(40)

The second term in the above equation is much smaller than that of first term.

Using E² = p²c² + m²c⁴ i.e. and in equation (33),

(41)

But, the energy and momentum operators are,

and

The above equation becomes,

(42)

Neglecting small terms from equation (40) and using large terms in equation (42),

by neglecting two terms
	(43)

Equation (43) is the TDSE in 1-D without potential energy term. In 3-D form it modifies to

where  is a Laplacian operator.

(44)

This approach of deriving TDSE from classical wave equation is important as this helps the students to understand the interlinkage between the classical theory of electrodynamics and the modern quantum mechanics.

Using Hamilton-Jacobi equation

The Hamilton equations can be obtained by applying Canonical transformation equations to the spatial coordinates q_i and canonical momenta p_i for n-dimensional classical mechanical system which are represented as

(45)

where, H is the Hamilton of the system at any instant t [9]. The canonical transformed coordinates Q_i and momenta P_i for n-dimensional system satisfies the Hamilton equation as

(46)

where, k is the transformed Hamiltonian related to the original H as

(47)

where, F is a generating function of the canonical transformation i.e. F(q_i, Q_i, t)

The another generating function is S called as Hamilton’s principle function represented as

S = F(q_i, P_i, t).

Due to which the transformed Hamiltonian k vanishes

(48)

The transformation equations for spatial coordinate q_i and momenta p_i are

(49)

Substituting equation (49) in equation (48),

(50)

Equation (50) is called as Hamilton-Jacobi equation.

For the particle with Newtonian mass m and potential V, the Hamilton-Jacobi equation will be,

(51)

The quantum wave function in terms of coordinate x is given by,

Taking log on both sides,

(52)

where, X = (x,y,z) is the space coordinate.

Differentiating equation (52) w.r. to x,y,z and t,

(53)

Differentiating first equation only from above equation w.r.to x,

(54)

Differentiating momentum coordinate equation from equation (49) w.r.to x by taking I → q → x,

(55)

From first equation in equation (53),

(56)

Substituting this value in equation (54) and using equation (55)

	(57)
Similarly,	(58)

Using equation (53) for t, equation (57) and (58) in equation (51)

(59)

The above equation is Time Dependent Schrödinger Equation in 3-D form. The Hamilton-Jacobi equation is basically related to classical mechanics and is particularly used where conserved quantities mechanical systems are to be identified. Deriving TDSE with this methodology helps to have similar treatment in quantum mechanics too.

Applications

Schrödinger’s equation is a fundamental or building block of quantum mechanics and finds several applications. Some of the significant applications are discussed in the following section.

1. Estimation of allowed energy levels of a particle in a constrained rigid box

Schrödinger equation is used to determine the allowed or permissible energy levels of quantum mechanical systems like atoms, electrons, protons, neutrons etc. The associated wave function gives the probability of finding the particle at a certain position. The allowed energy levels of a particle constrained to a rigid box can also be determined using SE.

The best example can be an electron in a thin conducting wire. Here, the electron can be considered to move freely back and forth along the length of the wire but cannot escape from it. Then, using SE, one can derive the expression for the allowed energies of the electron, as given below

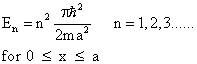
2. Investigation of possible energies of a free particle which are unconfined in any box

This is the case where the particle is not subjected to any forces and is completely unconfined. The potential energy of a free particle is constant and can be chosen to be zero. The SE can be set up and solved for such ‘free’ particle and the allowed energy levels can be determined.

3. Solutions to the problems related to tunnelling of a particle from different energy levels.

This is the fundamental basis for the modern characterization technique called Scanning Tunnelling Microscopy. SE can be used to comprehend the tunnelling or penetration of electrons through different energy levels.

The tunnelling current can be determined using solution to SE. Further, as the tunnelling current has a strong dependence on the surface morphology, the technique can then be directly applied to map the surface topography of a specimen.

4. Solutions to the problems related to step potential, square well potential in 1-D with different conditions for a particle.

Square well potential is a typical example or problem in quantum mechanics that exemplify differences between classical and quantum mechanical situations. This is analysed on the basis of energy of the particle which can be obtained only by solving SE. This underlines the utmost application.

5. Solutions to the problems related to a harmonic oscillator.

A simple harmonic oscillator is a system that oscillates about a stable equilibrium according to Hooke’s law. This situation resemble with vibrating atoms in a solid. The harmonic oscillator problem may be used to describe the vibrations of molecules. Again in this case, SE is the way to determine the potential energy, rather allowed energy levels, of vibrating atoms and to analyze their motion.

Conclusions

Discussion on Schrödinger’s equation, in particular, its derivation, is dealt with much complexity in books as well as during class room teaching. Present article is been an attempt to bridge this gap and to give a clear illustration of the concept along with its derivation, starting from many simpler concepts in classical mechanics. These ‘starting points’ included the equations from wave mechanics, Schrödinger Time Independent Equation, classical and Hamilton-Jacobi equations. It can be concluded that the article provides a stepping stone for the beginners in quantum mechanics, or the undergraduate students, to have an insight into SE and a varieties of way to derive it.

Acknowledgements

Authors (NPB, PPB) would like to thank Dr. R.S. Yennawar and Dr. S. A. Arote for the fruitful discussions and suggestions to enrich the manuscript

References

1. Pranab R. S., Direct Derivation of Schrödinger Equation from Hamilton-Jacobi Equation Using Uncertainty Principle, Romanian Journal of Physics, 2011, 56(9-10), p. 1053-1056.

2. Bodurov T., Derivation of the Nonlinear Schrödinger Equation from First Principles, Annales de la Fondation Louis de Broglie, 2005, 30(3-4), p. 343-352.

3. Ogiba F., Phenomenological Derivation of the Schrödinger Equation, Progress in Physics, 2011, 4, p. 25-28.

4. Piece P., Another Schrodinger Derivation of the Equation, Eur. J. Phys. 1996, 17, p. 116-117.

5. Ogborn J., Taylor E. F., Quantum Physics Explains Newton’s Laws of Motion, Phys. Educ. 2005, 40(1), p. 26-34.

6. Heisenberg W., Über Quantentheoretische Umdeutung Kinematischer und Mechanischer Beziehungen, Zeitschrift f¨ur Physik 1925, 33, 879.

7. Field J. H., Relationship of Quantum Mechanics to Classical Electromagnetism and Classical Relativistic Mechanics, Eur. J. Phys., 2004, 25, p. 385-397.

8. Hall M. J. W., Reginatto M., Schrodinger Equation from an Exact Uncertainty Principle, J. Phys. A, 2002, 35, p. 3289-3303.

9. Jackson J. D., Classical Electrodynamics, Wiley, New York, 3rd ed, 1999.

10. Schrödinger E., Quantization as an Eigenvalue Problem (First Communication), Annalen der Physik, 1926, 79, p. 361-376. [English translation in Gunter Ludwig Wave Mechanics 94-105 (Pergamon Press, 1968) ISBN 0-08-203204-1]

11. Schrödinger E., Quantization as an Eigenvalue Problem, (Second Communication) Annalen der Physik, 1926, 79, p. 489-527. [English translation in Gunter Ludwig Wave Mechanics 106-126 (Pergamon Press, 1968) ISBN 0-08-203204-1]

12. Schrödinger E., On the Relationship of the Heisenberg-Born-Jordan Quantum Mechanics to Mine, Annalen der Physik , 1926, 79, p. 734. [English translation in Gunter Ludwig Wave Mechanics 127-150 (Pergamon Press, 1968) ISBN 0-08-203204-1]

13. Schrödinger E., Quantization as an Eigenvalue Problem, (Fourth Communication) Annalen der Physik, 1926, 81, p. 109-139. [English translation in Gunter Ludwig Wave Mechanics 151-167 (Pergamon Press, 1968) ISBN 0-08-203204-1]

14. Feynman, R. P. “Space-Time Approach to Non-Relativistic Quantum Mechanics” Rev. Mod. Phys. 20, 1948, 367.

15. Dirac P. A. M., The Lagrangian in Quantum Mechanics”, Reprinted in ‘Selected Papers on Quantum Electrodynamics, Ed. Schwinger J. 1958, (New York: Dover) p. 312-320.

16. Vic Dannon H. Wave Particle Duality: de Broglie Waves and Incertainity, Gauge Institute Journal, 2006, 2(4), p. 1-19.

17. Briggs J. S., Rost J. M., On the Derivation of Time Dependent Equation of Schrödinger, Foundation of Physics, 2001, 31(4), p. 693-712.

18. Xavier A., et al, A Review of Transparent and Artificial Boundary Conditions Techniques for Linear and Nonlinear Schrödinger Equations, Communications in Computational physics, 2008, 4(4), p. 729-796.

19. Dubeibe F. L., Solving the Time Independent Schrödinger Equation with Absorbing Boundary Conditions and Source Terms in Mathematical 6.0”, International Journal of Modern Physics C, 2010.

20. Lajos Diosi, Classical-Quantum Coexistence: a ‘Free Will’ test, IOP Publishing, Journal of Physics: Conference Series, 2012, 361, 012028.

21. Putnam H., A Philosopher Looks at Quantum Mechanics (Again), Brit. J. Phil. Sci., 2005, 56, p. 615-634.