Fourth Zagreb index of Circumcoronene series of Benzenoid

Mohammad Reza FARAHANI^1* and Rajesh M. R. KANNA²

¹ Department of Applied Mathematics, Iran University of Science and Technology (IUST) Narmak, Tehran, 16844, Iran

² Department of Mathematics, Maharani's Science College for Women, Mysore- 570005. India

E-mails: ^*mr_farahani@mathdep.iust.ac.ir, mrfarahani88@gmail.com, Mr.rajeshkanna@gmail.com

^* Corresponding author, phone: +98-919-2478265

Abstract

A topological index of a graph is a numeric quantity related to a structure of a molecule which is invariant under graph automorphism. Recently, Ghorbani and Hosseinzadeh introduced Fourth Zagreb index of graphs. In this paper we determine a closed formula of this new topological index of the famous Benzenoid family named Circumcoronene series of Benzenoid H_k.

 Keywords

Molecular graph; Benzenoid graph; Circumcoronene series of benzenoid; Topological index; Eccentricity index; Fourth Zagreb index

Introduction

A molecular graph is a simple graph such that its vertices correspond to the atoms and the edges to the bonds. All graphs in this paper are finite and simple. For terms and concepts not defined here we refer the reader to any of several standard monographs such as e.g. [1-5].

Mathematical chemistry is a branch of theoretical chemistry for discussion and prediction of the molecular structure using mathematical methods without necessarily referring to quantum mechanics. Chemical graph theory is a branch of mathematical chemistry which applies graph theory to mathematical modelling of chemical phenomena [1-5]. This theory had an important effect on the development of the chemical sciences.

A graph invariant is any function on a graph that does not depend on a labelling of its vertices. Such quantities are also called topological indices. One of the best known and widely used is the Zagreb topological index introduced in 1972 by Gutman and Trinajstić and is defined as the sum of the squares of the degrees of all vertices of G [2, 5]. Let G be a connected graph with vertex and edge sets V(G) and E(G), respectively.

For every vertex uÎV(G), the edge connecting u and v is denoted by uv and d_G(u) (or d_u) denotes the degree of u in G (the number of first neighbors of vertex u in G).

The Zagreb indices were originally defined as follows:

M₁(G)=∑_{v Î V(G)} (d_v)²

M₂(G)=∑_{e=uv Î E(G)} (d_u×d_v)

here M₁(G) and M₂(G) denote the first and the second Zagreb index, respectively. The first Zagreb index can be also expressed as a sum over edges of G,

M₁(G)=∑_{e=uv Î E(G)} (d_u+d_v)

The readers interested in more information and some mathematical properties of Zagreb indices for general graphs can be referred to [5-11].

In 2012, Ghorbani and Hosseinzadeh introduced a new version of Zagreb index [12] as follows:

M**₁(G)=∑_{v Î V(G)} ε(v)²

In which for a vertex v of V(G) its eccentricity ε(v) is the largest distance between v and any other vertex u of G.

ε(v)=Max{d(u,v)|"uÎV(G)}

The maximum eccentricity over all vertices of G is called the diameter of G and denoted by D(G). Also the minimum eccentricity among vertices of G is called the radius and denoted by r(G). In other words,

D(G)=Max_vÎV(G){d(u,v)|"uÎV(G)}

R(G)=Min_vÎV(G){Max{d(u,v)|"uÎV(G)}}

The eccentric connectivity index ζ(G) of a graph G is defined as:

ζ(G)=∑_{v Î V(G)} d_v×ε(v)

For further study and more details see references [13-17].

The aim of this paper is to investigate a closed formula of new topological Zagreb index for Circumcoronene series of Benzenoid H_k (k≥1). In this paper, we call this new Zagreb index by Fourth Zagreb index and denote by M₄(G).

Material and method

In this section it is presented how to compute this new topological index for Circumcoronene series of Benzenoid H_k (k≥1). The Circumcoronene series is part of Benzenoid molecular graph family (consist several copy of benzene C₆). The general representation and some first members of this Benzenoid graph family are shown in Figures 1 and 2 (see [14-20]).

Figure 1. Some first members of Circumcoronene series of Benzenoid H_k (k≥1) [14-17]

In this article we use Cut method and Ring-cut method. Further studies on Cut Method and its modified version Ring-cut method can be seen in [19, 20]. Ring-cut method divides all vertices of G into some partitions with similar mathematical and topological properties. For example, readers can see ring-cuts of Circumcoronene series of Benzenoid in Figure 2.

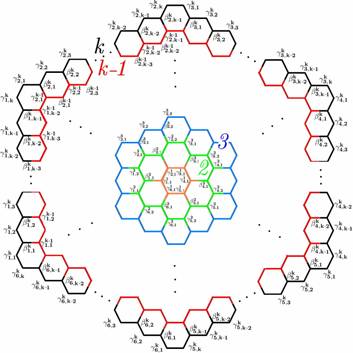
Figure 2. The Ring-cuts for the general representation of Circumcoronene series of Benzenoid H_k (k≥1) [14-17]

Thus, from the general representation of Circumcoronene series of Benzenoid H_k and its ring-cuts in Figure 2, one can see that [14-20]:

I. The vertex/atom set of H_k is V(H_k)={ |iÎZ_k & jÎZ_i & zÎZ₆}.

II. The edge/bond set of H_k is

E(H_k)={| iÎZ_k & jÎZ_i & zÎZ₆}.

III. The number of vertices is n_k=|V(H_k)|=6=6k² .

IV. The number of edges is e_k=|E(H_k)|=6+6k=9k²-3k.

V. "i=1..,k; jÎZ_i-1 & zÎZ₆: =2(k+i+1).

VI. "i=1..,k; jÎZ_i & zÎZ₆: =2(k+i)-1.

VII. The radius number of H_k is equal to r(H_k)=2k+1.

VIII. The diameter number of H_k is equal to D(H_k)=4k-1.

IX. ζ(H_k)=60k³-24k²-18k+18.

where all vertices are from I^th ring cut R_i of H_k., such that i=1,…, k and jÎZ_i & zÎZ₆ (Z_n is the cycle finite group of order n).

Results

Now, we can exhibit the closed formula of Fourth Zagreb index M₄(H_k) in following theorem and its proof.

Theorem 1: Let G be the Circumcoronene series of Benzenoid H_k (k≥1). Then Fourth Zagreb index of H_k is equal to:

M**1(Hk)=M4(Hk)=68k^4+4k^3-65k^2+71k-24

(1)

Proof: Consider Circumcoronene series of Benzenoid G=H_k (k≥1) as shown in Figure 2. Thus, we refer to definition of Fourth Zagreb index M₄(H_k) and compute this index for G=H_k in general case (kÎZ) as follows:

M**1(Hk)=∑v Î V(Hk) ε(v)^2 Þ

(2)

M4(Hk)=	(3)
= = =6i(2k+2i-1)^2+6(i-1)(2k+2i-2)^2 =6i(4k^2+4i^2+8ki-4k-4i+1)+6 (i-1)(4k^2+4i^2+8ki-8k-8i+4) =(12k^4+24k^3+12k^2)+(32k^4+16k^3-32k^2-16k)+(24k^4-36k^3-21k^2+39k)   -(24k^2-48k+24)

Finally, "kÎ Z, the Fourth Zagreb index is equal to:

M4(Hk)=68k^4+4k^3-65k^2+71k-24

(4)

Obviously, M₄(H₁=C₆)=6(3)²=54 and the proof is complete.

Conclusion

In this paper, we have computed closed formula of Fourth Zagreb index for famous Benzenoid molecular graph "Circumcoronene series of Benzenoid H_k (k≥1)".

                        References

1. Gutman I., Trinajstić N., Graph theory and molecular orbitals, Total π−electron energy of alternant hydrocarbons, Chem Phys Lett, 1972, 17, p. 535-538.

2. Randić M., On characterization of molecular branching, J. Am. Chem. Soc. 1975, 97, p. 6609-6615.

3. West D. B., Introduction to Graph Theory, Upper Saddle River, Prentice Hall, 1996.

4. Todeschini R., Consonni V., Handbook of Molecular Descriptors. Wiley, Weinheim, 2000.

5. Gutman I., Das K. C., The first Zagreb index 30 years after, MATCH Commun Math Comput Chem, 2004, 50, p. 83-92.

6. Farahani M. R., Computing Zagreb index, Zagreb Polynomial and some Connectivity index of Circumcoronene series, Advances in Materials and Corrosion, 2013, 2, p. 16-19.

7. Nikolic S., Kovacevic G., Milicevic A., Trinajstić N., The Zagreb indices 30 years after, Croat Chem Acta, 2003, 76, p. 113-124.

8. Braun J., Kerber A., Meringer M., Rucker C., Similarity of molecular descriptors: the equivalence of Zagreb indices and walk counts, MATCH Commun Math Comput Chem, 2005, 54, p. 163-176.

9. Khalifeh M. H., Yousefi-Azari H., Ashrafi A. R., The first and second Zagreb indices of graph operations, Discr Appl Math, 2009, 157, p. 804-811.

10. Zhou B., Gutman I., Relations between Wiener, hyper–Wiener and Zagreb indices, Chem Phys Lett, 2004, 394, p. 93-95.

11. Farahani M. R., Zagreb index, Zagreb Polynomial of Circumcoronene Series of Benzenoid, Advances in Materials and Corrosion, 2013, 2, p. 16-19.

12. Ghorbani M., Hosseinzadeh M. A., A New Version of Zagreb Indices, Filomat, 2012, 26(1), p. 93-100.

13. Ashrafi A. R., Ghorbani M., Hemmasi M., Eccentric connectivity polynomial of an infinite family of Dendrimer, Digest Journal of Nanomaterials and Biostructures, 2009, 4(3), p. 483-486.

14. Alikhani S., Iranmanesh M. A., Eccentric connectivity polynomial of an infinite family of Dendrimer, Digest Journal of Nanomaterials and Biostructures, 2011, 6(1), p. 253-257.

15. Farahani M. R., Computing Eccentricity Connectivity Polynomial of Circumcoronene Series of Benzenoid H_k by Ring-Cut Method. Annals of West University of Timisoara-Mathematics and Computer Science, 2013, 51(2), p. 29-37.

16. Farahani M. R., Modified Eccentric Connectivity polynomial of Circumcoronene Series of Benzenoid H_k, Journal of Advances in Physics, 2013, 2(1), p. 48-52.

17. Farahani M. R., Eccentricity Version of Atom-Bond Connectivity Index of Benzenoid Family ABC₅(H_k), World Applied Sciences Journal, 2013, 21(9), p. 1260-1265.

18. John P. E., Khadikar P. V., Singh J., A method of computing the PI index of Benzenoid hydrocarbons using orthogonal cuts, J Math Chem, 2007, 42(1), p. 27-45.

19. Klavžar S., Gutman I., Mohar B., Labeling of Benzenoid Systems which Reflects the Vertex-Distance Relations, J Chem Int Comput Sci, 1995, 35, p. 590-593.

20. Klavžar S., A Bird’s Eye View of The Cut Method and a Survey of Its Applications in Chemical Graph Theory, MATCH Commun Math Comput Chem, 2008, 60, p. 255-274.