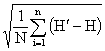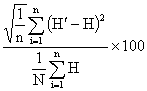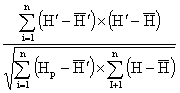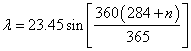Daily global solar radiation modelling using multi-layer perceptron neural networks in semi-arid region

Mawloud GUERMOUI^*, Abdelaziz RABEHI, Said BENKACIALI, Djelloul DJAFER

Unité de Recherche Appliquée en Energies Renouvelables, URAER, Centre de Développement des Energies Renouvelables, CDER, 47133, Ghardaïa, Algeria

E-mail (^*): gue.mouloud@gmail.com

^* Corresponding author, phone: 00(213)029 87 01 26, fax: 00(213)029 87 01 46

Received: March 19, 2016 / Accepted: July 14, 2016 / Published: July 31, 2016

Abstract

Accurate estimation of Daily Global Solar Radiation (DGSR) has been a major goal for solar energy application. However, solar radiation measurements are not a simple task for several reasons. In the cases where data are not available, it is very common the use of computational models to estimate the missing data, which are based mainly of the search for relationships between weather variables, such as temperature, humidity, sunshine duration, etc. In this respect, the present study focuses on the development of artificial neural network (ANN) model for estimation of daily global solar radiation on horizontal surface in Ghardaia city (South Algeria). In this analysis back-propagation algorithm is applied. Daily mean air temperature, relative humidity and sunshine duration was used as climatic inputs parameters, while the daily global solar radiation (DGSR) was the only output of the ANN. We have evaluated Multi-Layer Perceptron (MLP) models to estimate DGSR using three year of measurement (2005-2008). It was found that MLP-model based on sunshine duration and mean air temperature give accurate results in term of Mean Absolute Bias Error, Root Mean Square Error, Relative Square Error and Correlation Coefficient. The obtained values of these indicators are 0.67 MJ/m², 1.28 MJ/m², 6.12%and 98.18%, respectively which shows that MLP is highly qualified for DGSR estimation in semi-arid climates.

Keywords

Global Solar Radiation; Neural Network; Regression; Renewable Energy

Introduction

With increasing demands and interest in energy conservation and environmental protection, solar energy research has witnessed a growing interest and attracted a great deal of attention. Solar radiation is one of the most promising potential renewable energy sources which are believed to be cheap and clean energy in most regions.

The received solar radiation on earth surface depends upon climatic conditions of a location and geographical characteristic of the studied area. An optimal use of solar energy needs an accurate knowledge of solar radiation at a particular geographical location. Nevertheless, these data are not always dispensable particularly in isolated areas, in this respect several approaches have been developed in the literature for modeling and predicting solar radiation components such as: (i) empirical models [1-2], (ii) remote sensing retrievals [3-4] and (iii) soft computing using artificial neural network [5-6]. Many empirical regression models was proposed in the literature for estimating solar radiation, the most popular model was that proposed by Angström-Prescott [7] which establishes a simple relationship between global radiation and sunshine duration according to equation 1:

Rs/Ra = (S/S0)+b

(1)

where Rs is actual solar radiation, Ra is extra-terrestrial solar radiation, S is actual sunshine duration, so is potential sunshine duration, a and b are empirical parameters [8].

In recent years, several studies have been presented by researcher using many meteorological data to estimate the Daily Global Solar Radiation (DGSR). Due to the limited number of solar radiation measuring stations, the estimation of solar radiation are necessary.  In this respect new models and improvement are continually proposed which intend to improve the solar radiation values based on available meteorological variables. As mentioned before, Artificial Neural Network (ANN) which used widely to estimate and predict solar radiation is one of the earliest machine learning methods. The main issues of ANN include its instability with short data and its tendency to over fit training data. Dorvio et al [9], used Radial Basis Functions (RBF) and Multi-Layer Perceptron (MLP) networks to estimate the solar radiation from eight stations in Oman. It was pointed out that, in terms of RMSE between the observed and predicted solar radiation values, both the RBF and MLP models performed well, (0.83 MJ/m2/day) was obtained for the RBF and (1.01 MJ/m2/day) for the MLP. Banghanem et al. [5] used Radial Basis Functions (RBF) neural network to estimate DGSR at Al-Madina (Saudi Arabia). Four RBF models were developed using different meteorological data as input, it was found that the RBF model that uses sunshine duration and air temperature as input gives high performance (r = 98.8%). Senkal et al. [10] used MLP for estimating of the DGSR at 12 cities in Turkey using latitude, longitude, altitude, month, mean diffuse radiation and mean beam radiation as input whereas the output of the network is the solar radiation. According to the authors the MLP model performs better than the physical model, the obtained RMSE between the estimated values using the MLP and the physical model was 91 W/m² and 125 W/m² (testing cities), respectively.

Sozen et al. [11] proposed a neural network model for modeling solar radiation based on geographical coordinates (latitude, longitude and altitude), meteorological data (sunshine duration and mean temperature) and the corresponding month from seventeen stations in Turkey as inputs of the network. According to the others, the maximum mean absolute percentage error was found to be less than 6.7% and the correlation coefficient achieves 99.89% for the testing stations. Another interesting work proposed in [12] using hybrid model that combines Markov chain and neural network called ANN-MTM (Markov Transition Matrix). The geographic coordinates was used as input of the proposed model while the outputs are the DGSR. The obtained results between the measured and the predicted data generated by the proposed model in term of root mean square error (RMSE) is below 8% and the correlation coefficient between 90 and 92%.

Artificial neural network

Artificial neural network models employ artificial intelligence techniques and are data driven; they learn and memorize a data structure and subsequently simulate the structure.

ANN can be trained to be used to approximate a non-linear function [12], or to classify outputs [13].There are several algorithms available to train a neural network but this depends on the type of the topology of the neural networks. The aim of the present study is represented by developing artificial neural network (ANN) model for estimation of daily global solar radiation on horizontal surface in Ghardaia city (South Algeria).

The most prominent topology of ANN is the feed-forward networks. An ANN is composed of nodes organized into layers and connected through weight elements. At each node, the weighted inputs are aggregated, threshold and inputted to an activation function to generate an output of that nod. Mathematically, this can be represented by equation 2:

y(t) = f

(2)

x_i are neuron inputs, w_i are the weights and f[.] is the activation function.

Multilayer Feed-forward is a kind of neural network, which consist of a number of layers: the first has neurons directly connected to the input data, and they are linked to one or more neurons in a hidden layer, or directly connected to the neurons in the output layer. In this kind of network, all neurons in one layer are full connected to all neurons of the next layer, and there are no feedbacks or recurrent connections.

In this work, was used a Multilayer Feed-forward Neural Network with different inputs parameters, as show in Figure 1. Hyperbolic tangent sigmoid transfer function is used in the hidden layer and linear transfer function for neurons in the output layer. The neural network was trained with the Leven-berg-Marquardt Back-propagation algorithm [14], due to its high efficiency and fast convergence, although their computational requirements are high.

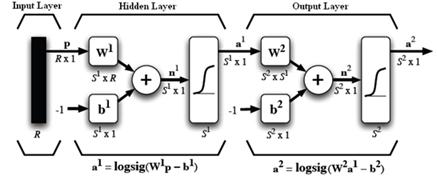
Figure 1. Architecture of MLP neural network

Materials and methodology

Site location and solar radiation data

The experimental data used in this work (Global Solar Radiation and sunshine duration, air temperature, relative humidity) , have been collected at the Applied Research Unit for Renewable Energies, (URAER) situated in the south of Algeria far from Ghardaïa city with latitude: +32.37°, longitude: +3.77°, and altitude of 450 m above the mean sea level Figure 2.

Figure 2. Location of the studied sites

The climate of Ghardaia region is semi-arid with a minimum and maximum air temperatures ranging from 14°C to 47°C and from 2°C to 37°C during summer and winter months respectively. The daily GSR varies between a minimum of 607Wh/m2/day to a maximum of 7574Wh/m2/day and the annual-mean-daily GSR is about 5656Wh/ m²/day. The data are recorded every 5 min with a high precision by a radiometric station installed at the rooftop of the URAER (Unité de Recherche Appliquée en Energie Renouvelable) as shown on Figure 3.

Figure 3. Instrumentation station

The prediction model uses the data collected between 2005 and 2008 (for some days, however, there is no information due to electrical outages).The daily evolution of global solar radiation on horizontal surfaces and sunshine duration is illustrated in Figure 4.

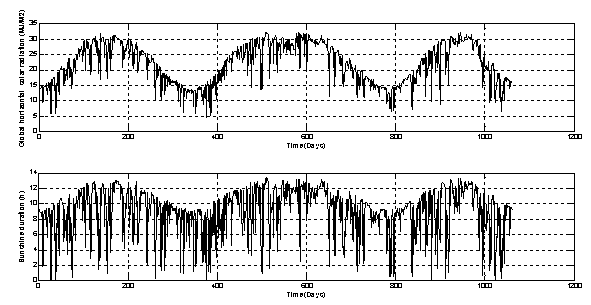
Figure 4. Daily evolution of the global horizontal radiation and sunshine duration

Model validation

The performance of MLP models for estimating DGSR on horizontal surface is evaluated by comparing the estimated values with the measured values using different statistical indexes such as Mean Absolute Bias Error (MABE), Root Mean Square Error (RMSE), Relative Square Error (RRMSE), Determination Coefficient (R²) and Correlation Coefficient(r). The MABE, give the mean absolute value of bias error. Its expression is given by equation 3:

MABS = f

(3)

where is the estimated value and is the measured value. The RMSE represents the difference between the predicted values and the measured values. In fact, RMSE identifies the model's accuracy. It is calculated by:

RMSE = f

(4)

The RRMSE is calculated by dividing the RRMSE to the average of measured data as:

RRMSE = f

(5)

The performance of the model is defined by the RRMSE range as follows:

· Excellent if: RRMSE≤10

· Good if: 10% < RMSE < 20%, 10 ≤ RRMSE ≤ 20

· Fair if: 20% < RMSE < 30%, 20% ≤ RRMSE ≤ 30%

· Poor if: RMSE > 30%, RMSE ≥ 30%

The R² and r indicate the strength of a linear relationship between the measured and predicted values. They are calculated as follows:

r = f

(6)

MLP-based implementation of solar radiation models

As mentioned before, the main objective of this letter is to assess the potential of MLP for modeling the global solar radiation from other parameters (e.g. Air temperature, Sunshine Ratio, Relative Humidity) in semi arid area (Ghardaia). In this respect several MLP-models are developed based on different input parameters and one output (which is the Clearness Index ).

Several combinations of the input parameters are used; we take Air Temperature, Relative Humidity and sunshine ration (SS) as inputs and clearness index, K_T = H/H₀ as output.

The collected data are divided into three subsets, first set for training (600 samples), the second (100 sample) for model validation and the rest for testing the performance of the studied MLP-models. The obtained statistical results are presented in Table1 for the testing data set. From Table 1, we can infer several observations. Firstly, we can point out that using different inputs influence the precision of the models. Secondly, MLP models that use air temperature achieve high performance compared with those based on relative humidity. Thirdly, combining air temperature and relative humidity does not improve significantly the performance of the models.

An important observation is that using sunshine ratio alone as input achieves high performance due to its high correlation with clearness index. Combining sunshine duration with air temperature and relative humidity boosts the performance and the model with higher accuracy are obtained using {T_Mean, SS} as input parameters.

Table 1. The studied MLP-models with different input attributes

Models	Input Parameters	MABE (MJ/m^2)	RMSE (MJ/m2)	RRMSE	r(%)
MLP-1	TMean, HMean	2.12	3.05	14.6	89.15
MLP-2	TMean, HMean,SS	0.76	1.38	6.59	97.98
MLP-3	TMean,,SS	0.75	1.28	6.12	98.18
MLP-4	HMean, SS	0.84	1.33	6.36	98.06
MLP-5	SS	0.91	1.55	7.42	97.27

The graphical prediction output of the all five MLP- models against the measured data is plotted in the Figures (4-8) as follow:

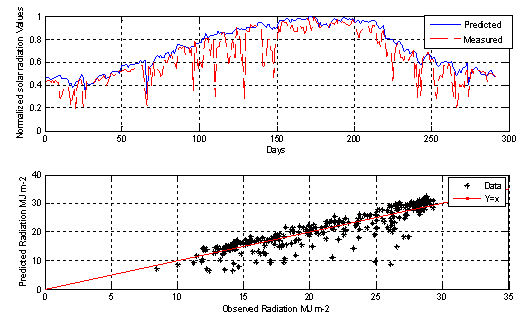
Figure 4. MLP-1 model output prediction

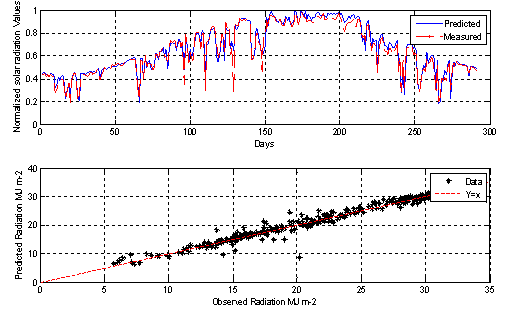
Figure 5. MLP-2 model output prediction

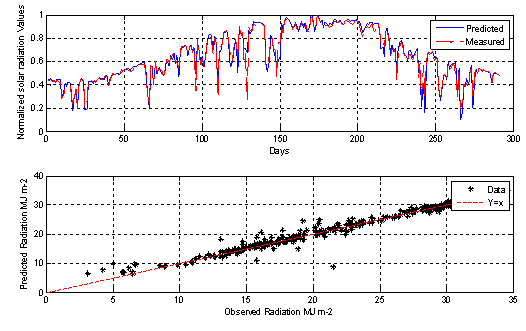
Figure 6. MLP-3 model output prediction

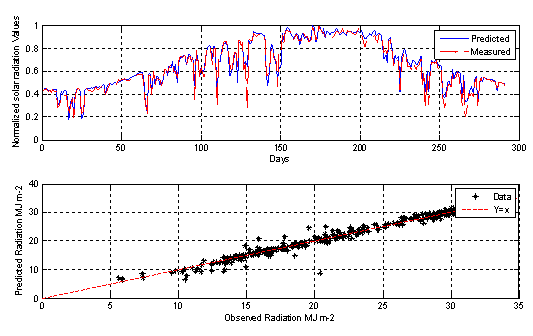
Figure 7. MLP-4 model output prediction

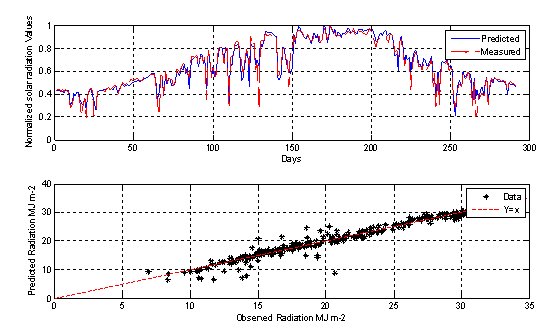
Figure 8. MLP-5 model output prediction

Conclusion

The conducted examination showed the appreciable effect of input parameters on the precision of MLP-models. It has been demonstrated that H = {SS, T_Mean} provides better accurate precision than the other proposed MLP-models.

It should be noted that the fraction of sunshine duration SS play an important role for obtaining high precision accuracy which has been seen in the case when we have eliminated the fraction of sunshine duration from the input of the MLP-models.

Additionally, more cases studies with various climate conditions should also be considered in the future investigations.

Acknowledgements

We would like to thank and acknowledge the support of the team at the Research Unit on Renewable Energies of Ghardaïa who collected the data used in the present study.

Appendix

Clearness index K_T, which is the ratio of global solar radiation on horizontal surface (H) to the extraterrestrial solar radiation on horizontal surface (H₀).The extra-terrestrial solar radiation (H₀) is given as:

H0 =

(7)

where I₀ is the solar constant equal to 1360 W/m², f is the eccentricity correction factor, λ is the latitude of the region, δ is the solar declination and w_s is the mean sunrise hour angle, n represents the number of days.

References

1. Besharat F., Dehghan A. A., Faghih A. A., Empirical models for estimating global solar radiation: A review and case study, Renewable and Sustainable Energy Reviews, 2013, 21, p. 798-821.

2. Gueymard C. A., Clear-sky irradiance predictions for solar resource mapping and large-scale applications: Improved validation methodology and detailed performance analysis of 18 broadband radiative models, Solar Energy, 2012, 86(8), p. 2145-2169.

3. Pinker R. T., Frouin R., Li Z., A review of satellite methods to derive surface shortwave irradiance, Remote Sensing of Environment, 1995, 51(1), p. 108-124.

4. Pinker R. T., Kustas W. P., Laszlo I., Moran M. S., Huete A. R., Bas in scale solar irradiance estimates in semiarid regions using GOES, Water Resources Research, 1994, 30(5), p. 1375-1386.

5. Benghanem M., Mellit A., Radial basis function network-based prediction of global solar radiation data: application for sizing of a stand-alone photovoltaic system at Al-Madinah, Saudi Arabia, Energy, 2010, 35(9), p. 3751-3762.

6. Kumar Y. A., Chandel S. S., Solar radiation prediction using Artificial Neural Network techniques: A review, Renewable and Sustainable Energy Reviews, 2014, 33, p. 772-781.

7. Prescott J. A., Evaporation from a water surface in relation to solar radiation, Transactions of the Royal Society of South Australia, 1940, 64:114-118.

8. Chen J. L., Li G. S., Wu S. J., Assessing the potential of support vector machine for estimating daily solar radiation using sunshine duration, Energy Conversion and Management, 2013, 75, p. 311-318.

9. Dorvlo A. S., Jervase J. A., Al-Lawati A., Solar radiation estimation using artificial neural networks, Applied Energy, 2002, 71(4), p. 307-319.

10. Şenkal O., Kuleli T., Estimation of solar radiation over Turkey using artificial neural network and satellite data, Applied Energy, 2009, 86(7), p. 1222-1228.

11. Sözen A., Arcaklioğlu E., Özalp M., Estimation of solar potential in Turkey by artificial neural networks using meteorological and geographical data, Energy Conversion and Management, 2004, 45(18), p. 3033-3052.

12. Mellit A., Benghanem M., Arab A. H., Guessoum A., A simplified model for generating sequences of global solar radiation data for isolated sites: Using artificial neural network and a library of Markov transition matrices approach, Solar Energy, 2005, 79(5), p. 469-482.

13. Guermoui M., Mekhalfi M. L., Ferroudji K., Heart sounds analysis using wavelets responses and support vector machines. In Systems, Signal Processing and their Applications (WoSSPA), 8th International Workshop, IEEE, 2013, p. 233-238.

14. Hagan M. T., Menhaj M. B., Training feed forward networks with the Marquardt algorithm, IEEE Transactions on Neural Networks, 1994, 5(6), p. 989-993.