Design and implementation of efficient low complexity biomedical artifact canceller for nano devices

Md Zia Ur RAHMAN^*, Asiya SULTANA, Burra Venkata SRIKANTH

Department of ECE, K L University, Green Fields, Guntur DT, AP, 522502, India

Emails: mdzr@kluniversity.in; asiyabits50@gmail.com; srikanthsesha8@gmal.com

^* Corresponding author, phone:  +91-9440712707

Received: March 19, 2016 / Accepted: July 17, 2016 / Published: July 31, 2016

Abstract

In the current day scenario, with the rapid development of communication technology remote health care monitoring becomes as an intense research area. In remote health care monitoring, the primary aim is to facilitate the doctor with high resolution biomedical data. In order to cancel various artifacts in clinical environment in this paper we propose some efficient adaptive noise cancellation techniques. To obtain low computational complexity we combine clipping the data or error with Least Mean Square (LMS) algorithm. This results sign regressor LMS (SRLMS), sign LMS (SLMS) and sign LMS (SSLMS) algorithms. Using these algorithms, we design Very-large-scale integration (VLSI) architectures of various Biomedical Noise Cancellers (BNCs). In addition, the filtering capabilities of the proposed implementations are measured using real biomedical signals. Among the various BNCs tested, SRLMS based BNC is found to be better with reference to convergence speed, filtering capability and computational complexity. The main advantage of this technique is it needs only one multiplication to compute next weight. In this manner SRLMS based BNC is independent of filter length with reference to its computations. Whereas, the average signal to noise ratio achieved in the noise cancellation experiments are recorded as 7.1059dBs, 7.1776dBs, 6.2795dBs and 5.8847dBs for various BNCs based on LMS, SRLMS, SLMS and SSSLMS algorithms respectively. Based on the filtering characteristics, convergence and computational complexity, the proposed SRLMS based BNC architecture is well suited for nanotechnology applications.

Keywords:

Artifacts; Biomedical noise cancellers; Computational complexity; Remote health care monitoring, Very-large-scale integration architectures

Introduction

Remote health care monitoring works by communicating the physiological information between patient and the medical examiner. During the signal acquisition using sensors from the patient, several artifacts, both physiological and non-physiological quantities contaminates signal quality. These artifacts mask the tiny features of the biomedical signals and makes ambiguities in diagnosis. In addition to these artifacts, in remote monitoring, during the data transmission through free space; channel noise also contaminates the signal [1,2]. Chronic Diseases (CD) refers to a large number of medical conditions relating to the functionality of various key organs. According to World Health Organization (WHO) every year millions of people in this industrialized world are getting affected with cardio vascular diseases (CVDs) and as a result it is necessary to see that the treatment must be given in a faster manner, also WHO reports that neurological disorders are important cause of mortality and constitute 12% of total deaths globally. Among the neurological disorders, cerebro-vascular diseases are responsible for 85% of the deaths [3-9]. In these scenarios, remote health care monitoring plays a vital role for proper diagnosis and immediate action when the patient is far from the hospital.

This includes the capability for monitoring biological condition of the patient with less effort and faithful reproduction of the data. In literature, several contributions are made during recent years on remote health care monitoring [10-16]. However, during acquisition of biological data from patient several artifacts contaminates the signal quality. The artifacts will spoil the signal in such a way that diagnosis will not be accurate. In addition to these artifacts, while transmitting the data to doctor’s end channel noise also effects the signal quality. As a result, to facilitate noise free high resolution at the receiving end, all the contaminations should be removed. Since the nature of the biomedical signal and the contaminations are non-stationery, adaptive filtering is a promising technique to eliminate the contaminations. In literature, several signal conditioning techniques are presented to eliminate artifacts from brain activity signals [17-19]. In these papers, authors proved the concept of elimination of artifacts to facilitate high resolution signals for diagnosis. In all these papers, only signal processing aspects for filtering the noise were discusses. To the best of author’s knowledge, none of the contributions have covered the Very-large-scale integration (VLSI) implementation of the filtering section.

Hence in this manuscript we propose the VLSI implementation of the techniques used in noise cancellation. This enables the development of Lab on Chip (LOC). Nowadays, with the rapid development of medical technology, both wearable and implantable devices play a key role in health care monitoring. Due to practical reasons, these devices should be in nano scale. In order to design a nano device, less computational complexity is desirable. This also reduces computational time, area of the circuit, power consumption and cost of implementation. Hence to achieve these advantages we design the filtering section with simplified algorithms.

There exist three simplified algorithms those are data sign regressor algorithm (SRA), sign error algorithm (SEA) and sign algorithm (SSA). These methodologies are applied on familiar LMS weight update recursion for the implementation of various BNCs. In [20-22], Rahman et al. presented several hybrid algorithms using the three simplified algorithms and normalized algorithms. In our implementations, we demonstrate the VLSI implementations as well as filtering aspects. To prove the filtering capability of the proposed implementations, we apply the techniques on real biomedical signals and performance measures are tabulated. Simulation results confirm that the proposed implementations are well suited to embed in a nano remote health care monitoring system.

Material and method

In a typical BNC section, adaptive filter can be used since both the signal and artifact are non-stationary components. In our implementation, also initially we consider a LMS algorithm for the implementation of BNC. Let us consider an L length transversal LMS adaptive filter as shown in Figure 1. In Figure 1, n₂ represents reference signal, which is somewhat correlated with the noise component present in the input bio-medical signal. Z^-1 is the delay between the samples, w_O(n) to w_L-1(n) are filter weights, L is the filter length, y(n) is the filter output, e(n) is error signal, s₁+n₁ is the input contaminated bio-medical signal.

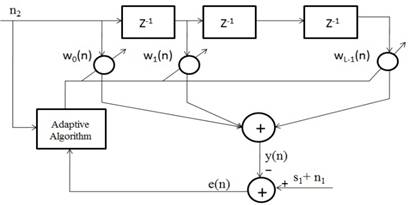
Figure 1. LMS based transversal adaptive filter

The weight update mechanism of LMS algorithm is given by the recursion (equation 1) [23]:

w(n+1) = w(n) + µe(n)x(n)

(1)

where µ is step size, e(n) is error calculated, x(n) is data regressor.

During acquisition of the biomedical signal s₁ several artifacts n₁ contaminates the signal component, hence the input to the BNC is contaminated signal s₁+n_1. In order to cancel the noise component, n₂ a noise component correlated with n₁ is given as reference signal to the noise canceller and we take that S₁, n₁ and n₂ are uncorrelated. Now we assume that s₁, n₁, n₂, and y are zero mean and stationary processes. The output e is given as:

e = S1+n1-y

(2)

Taking Expectation on both sides to the above equation and minimizing it we get:

E[e^2] = E[S1^2] +E[(n1 -y)^2] + 2E[S1(n1-y)]	(3)
E[e2] = E[S1^2] +E[(n1 -y)^2]	(4)
min E[e^2] = min E[S1^2] +min E[(n1 -y)^2]	(5)

When E [e²] reduces, then E [(n₁ – y)²] also gets reduced and y, e will be similar to n₁and S₁ respectively. As (5) reduces to a minimum value the error approaches the signal S₁ and noise reduces. It also leads to increase in SNR and the error will be exactly same as S₁. In this case, minimizing output power causes the output signal to be perfectly noise free. As error is given as feedback to the adaptive algorithm, the filter weights will adjust to the changing environment.

Implementation of simplified LMS algorithms

Sign based versions will have low computational complexity and are therefore suitable for nano technology based biotelemetry applications. In this section, we will apply signum function to various algorithms and enables BNC with less computational complexity.

These low computational complexity BNCs are suitable for nano health care monitoring systems. The convergence analysis of LMS and Signed algorithms leads to a conclusion that, signum based algorithms are just inferior to LMS algorithm [24, 25]. The familiar simplified algorithms are detailed in this section.

Sign Regressor LMS (SRLMS) algorithms obtained by replacing the input vector x(n) in LMS with Sign{x(n)}. The signed-regressor recursion is then given as,

W(n+1) = W(n) + µe(n)sign(x(n))

(6)

where:

Sign[x(n)] = 1: x(n) > 0 Sign[x(n)] = 0: x(n) = 0 Sign[x(n)] = -1: x(n) < 0

(7)

The k_th coefficient in the sign of the data vector may be written as follows:

(8)

In the sign regressor algorithm each data sample is normalized by the magnitude of the sample. This improves convergence as well as filtering performance. Due to this, even the data vector is clipped the performance is little inferior to LMS. When e(n) is clipped with signum function the algorithm becomes Sign LMS (SLMS)  The update equation is given as,

W(n+1) = W(n) + µsign(e(n))x(n)

(9)

When both the data and error are clipped with signum function the resultant algorithm is Sign-Sign LMS (SSLMS) algorithm. The update equation of the SSLMS algorithm is given as,

W(n+1) = W(n) + µsign(e(n))sign(x(n))

(10)

From (6) and (8) in SRLMS the filtering process of each sample is driven by a variable step size parameter. Here the selection of step size is based on the average size of x(n). This leads to a more homogeneous convergence of the signed regressor algorithm when compared with sign algorithm. Hence the performance of SRA is little bit inferior only. But in the case of SEA and SSA residual error remains due to error clipping, this leads to less resolution in the output signal [26,27]. The convergence characteristics are shown in Figure 2.

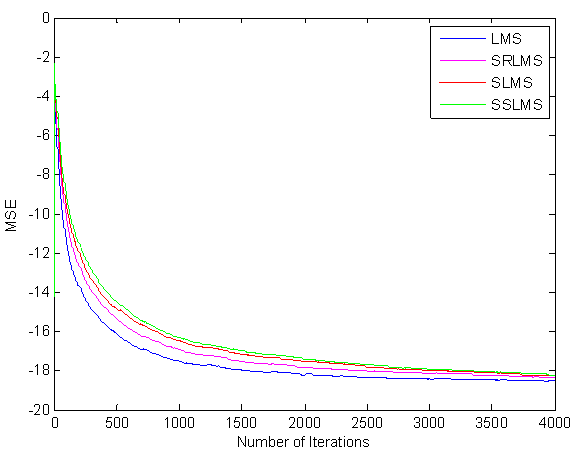
Figure 2.Convergence behavior of LMS and Simplified algorithms

From the Figure 2 it is clear that SRLMS is slightly inferior to LMS at the cost of minimum multiplications [28]. The goal of brain signal enhancement is to separate the valid components from the undesired artifacts and to present an EEG that facilitates easy and accurate interpretation [22]. In our simulations, the method has been validated using several EEG recordings with EBA obtained using the Emotive EPOC acquisition system [29] which has 14 data collecting sensors and 2 reference sensors. The sensors are placed according to the international 10-20 system and are labeled as such [30].

Computational complexity issues

Generally, to estimate and compare algorithm complexity number of multiplications required to complete the operation is taken as a measure. However, most of the DSP’s have a built in hardware support for multiplication and accumulation (MAC) operations. Usually they perform this operation in a single instruction cycle as well as addition or subtraction.

In this paper we are not trying to provide a precise analysis of a computational complexity, rather we concentrate on presenting a comparison between different adaptive algorithms. The computational complexity figures required to compute all the LMS based adaptive filters and their sign based realizations are summarized in Table 1, offers significant reduction in the number of operations required for LMS algorithm.

Table 1. Computational complexity of LMS and its sign based variants

S.No.	Algorithm	Multiplications	Additions	ASC
1	LMS	L+1	L+1	NIL
2	SRLMS	1	L+1	NIL
3	SLMS	L	L+1	NIL
4	SSLMS	NIL	NIL	L+1

Further, as these sign based algorithms are largely free from multiplication operation, these algorithms provides elegant means for removing the noise from the biomedical signals [20]. For example LMS algorithm L+1 multiplication and L+1 addition are required to compute the weight update equation (1), where L is the length of the filter. In case of signed regressor algorithm only one multiplication is required to compute μ e(n). Whereas other two signed LMS algorithms does not require multiplication if we choose μ value a power of 2.

In these cases multiplication becomes shift operation which is less complex in practical realizations. In SSA we apply signum to both data and vector, and then we add μ to weight vector with addition with sign check (ASC) operation [21].

Results and discussion

In our experiments to prove the ability of proposed implementations we carried our simulation in two different ways. One is VLSI implementation, to prove that low area, low power and low delay implementation suitable for nano devices can be achieved; another one is noise cancellation which proves that the above said techniques are effective.

Were implemented the algorithms in VERILOG taking the input signal length as eight, and the tap length is taken as 5, 10 and 15. Simulation is done using the Xilinx Design Simulator. Figures 3-6 shows the timing waveforms of the techniques.

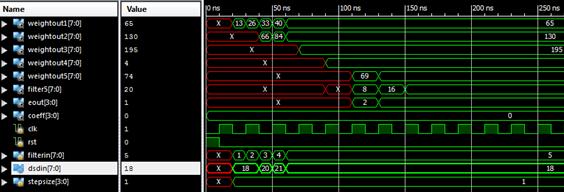
Figure 3.Waveform window showing the output of LMS simulation

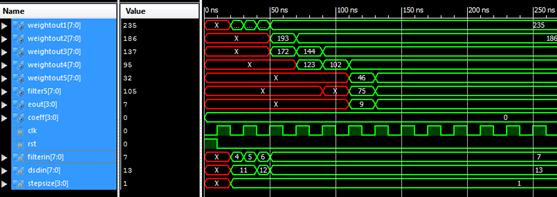
Figure 4. Waveform window showing the output of SRLMS simulation

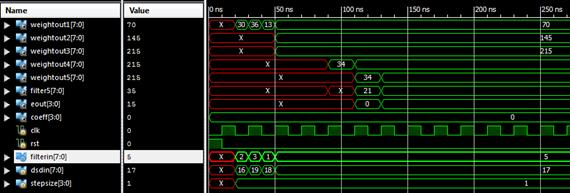
Figure 5. Waveform window showing the output of SLMS simulation

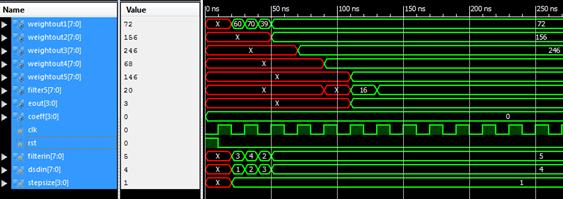
Figure 6. Waveform window showing the output of SSLMS simulation

The proposed technique utilized very less chip area and operated at high throughput rate compared to all the existing architectures. The design can be adapted to filters of any order and is particularly useful for filters of higher order and large base units. As the filter tap length increases then delay, number of LUT’s, power supply also increases. In-spite of the increase in all the parameters the consumed power is remaining approximately same. The consumed power is calculated from the supply power of field programmable gate array, to the number of look up tables used from the number of look up tables available from the synthesized Xilinix code. In the similar way the power consumed for all the architectures are shown in Table 2. Table 2 shows the comparison of power supply and power consumed in the proposed architectures for various algorithms.

Table 2. Comparison of various parameters with different tap length

Tap Length	Architecture	LUT's	Error out	Filter out	Path delay	Power supply	Power consumed
5	LMS	296	2	14	68.407	0.167	4.022mW
	SRLMS	304	2	6	68.407	0.167	4.13mW
	SELMS	310	2	14	66.326	0.168	4.23mW
	SSLMS	318	2	8	66.326	0.166	4.29mW
10	LMS	641	1	18	138.66	0.175	9.12mW
	SRLMS	649	2	12	138.66	0.171	9.03mW
	SELMS	707	1	27	139.785	0.17	9.43mW
	SSLMS	715	2	14	139.785	0.171	9.14mW
15	LMS	957	1	27	203.093	0.175	15.09mW
	SRLMS	987	2	10	207.369	0.178	14.29mW
	SELMS	1060	2	15	203.299	0.175	15.09mW
	SSLMS	1068	2	14	203.299	0.177	15.3mW

In LMS Filtering the noise is almost reduced and the filter is found to be tracking the signal better when the step size is optimum. Using the same filter tap lengths we implemented the techniques on Xilinx Vertex4 XC4VLX15 field programmable gate array.

To prove the ability of the proposed algorithms for filtering in real time environment, we implemented various BNCs using the LMS, SRLMS, SLMS and SSLMS as per the block diagram shown in Figure 1. For these simulations, we have taken Electro Encephalography (EEG) signal contaminated with Eye Blink Artifact (EBA). The acquisition system transmits encrypted data wirelessly to a machine; the wireless chip is proprietary and operates in the same frequency range as 802.11 (2.4GHz). Using this brain computer interface (BCI) system we have recorded brain signal contaminated with EBA.

Figure 7 shows the filtering results of various BNCs considered. In addition, Table 3 shows the performance of BNCs in filtering in terms of signal to noise ratio improvement (SNRI).

Figure 7. EBA Noise Cancelation in EEG Signal

Legend:
(a)	EEG with EBA
(b)	EEG after LMS based BNC
(c)	EEG after SRLMS based BNC
(d)	EEG after SLMS based BNC
(e)	EEG after SSLMS based BNC

Table. 3. SNRI Comparison of various algorithms in dBs

S.No	Record Number	LMS	SRLMS	SLMS	SSLMS
1	Record 1	7.8343	7.8757	6.4591	5.8771
2	Record 2	7.1989	7.2391	6.0935	5.6382
3	Record 3	6.7621	6.7964	6.2917	5.9075
4	Record 4	7.5826	7.7752	6.6893	6.3501
5	Record 5	6.1476	6.2018	5.8643	5.6509
Average		7.1059	7.1776	6.2795	5.8847

The EEG contaminated with EBA is given as input to the BNC shown in Figure 7 (a). Noise component correlated with EBA is given as reference to the noise canceller. The experiments are conducted on five data samples for ten times and average performance measures are tabulated. The filtering results are shown in Figure 7. We considered a data set of five EEG records contaminated with EBA. The noise cancellation experiment is performed for ten times and average values are tabulated in Table 3.

The SNRI, is used as performance measure and from the table it is clear that SRLMS achieves SNRI slightly superior to that of LMS based BNC. This is due to the data normalization operation performed by the signum function. The average signal to noise ratio achieved in the noise cancellation experiments are recorded as 7.1059dBs, 7.1776dBs, 6.2795dBs and 5.8847dBs for various BNCs based on LMS, SRLMS, SLMS and SSSLMS algorithms respectively.

Therefore among all the algorithms, SRLMS based BNC performs better in terms of computational complexity, convergence speed, SNRI. Hence this BNC is suitable for developing nano health care monitoring devices.

Conclusions

From the simulation results, it is clear that the tracking capability of the SRLMS based BNC is better than SLMS and SSLMS based BNCs. This is due to the data normalization embedded in the signum function. Due to this feature, SRLMS would little bit inferior in terms of convergence, but it is little bit superior in terms of filtering capability.

The BNC based on SRLMS needs only one multiplication for computing its recursion, i.e., the number of multiplications are independent of filter length. This feature enables SRLMS for practical realization of nano BNCs or lab on chip implementations for nano remote health care monitoring systems. 

References

1. Cromwell L., Weibell F. J., Pfeiffer E. A., Biomedical Instrumentation and Measurements, Prentice-Hall, 1980.

2. Guler N. F., Ubeyli E. D., Theory and Applications of Biotelemetry, Journal of Medical Systems, 2002, 26(2), p. 159-178.

3. Preventing chronic diseases a vital investment, World Health Organization, Geneva, 2005.

4. Prevention and control of non-communicable diseases: Implementation of global strategy, World Health Organization, Geneva, 2007.

5. Atlas: Epilepsy Care in the World, World Health Organization, Geneva, 2005, Neurological Disorders: Public Health Challenges, World Health Organization, Geneva, 2006.

6. Disease Control Priorities Related To Mental, Neurological, Developmental and Substance Abuse Disorders, World Health Organization, Geneva, 2006.

7. Brain and Eye Disease Researcher Survey, Bright Focus Foundation, 2012.

8. Neurological Diseases and Neuroscience, World Health Organization, Geneva, 2000.

9. Mazomenos E. B., Biswas D., Acharyya A., Chen T., Maharatna K., Rosengarten J., Morgan J., Curzen N., A Low-Complexity ECG Feature Extraction Algorithm for Mobile Healthcare Applications, IEEE Journal of Biomedical and Health Informatics, 2013, 17(2), p. 459-469.

10. Sriraam N., A High-Performance Lossless Compression Scheme for EEG Signals Using Wavelet Transformand Neural Network Predictors, International Journal of Telemedicine and Applications, 2012, p .1-9.

11. Singh M., Jindal I., Agarwal A., Pant P., V. Sinham, Kumar M. R., Kuma M., Jaiswal N., Application of Handheld Tele-ECG for Health Care Deliveryin Rural India, International Journal of Telemedicine and Applications, 2014, p.1-7.

12. Abo-Zahhad M., Ahmed S. M., Elnahas O., A Wireless Emergency Telemedicine System for Patients Monitoring and Diagnosis, International Journal of Telemedicine and Applications, 2014, 2014, Article ID 380787.

13. Chen T., Mazomenos E.B., Maharatna K., Dasmahapatra S., Niranjan M., Design of a Low-Power On-Body ECG Classifier for Remote Cardiovascular Monitoring Systems, IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2013, 3(1), p. 75-85.

14. Zhang Y., Wei S., Long Y., Liu C., Performance Analysis of Multi-scale Entropy for the Assessment of ECG Signal Quality, Journal of Electrical and Computer Engineering, 2015, p. 1-9.

15. Kyungtae Kang, An Adaptive Framework for Real-Time ECG Transmission in Mobile Environments, The Scientific World Journal, 2014, (2014), Article ID 678309.

16. Petrantonakis P. C., Hadjileontiadis L. J., Adaptive emotional information retrieval from EEG signals in the time-frequency domain, IEEE Transactions on Signal Processing, 2012, 60(5), p. 2604-2616.

17. Daly I., Billinger M., Scherer R., Muller Putz G., On the automated removal of artifacts related to head movement from the EEG, IEEE Transactions on Neural Systems and Rehabitation Engineering, 2013, 21(3), p. 427-434.

18. Noureddin B., Lawrence P. D., Birch G. E., Online removal of eye movement and blink EEG artifacts using a high-speed eye tracker, IEEE Transactions on Biomedical Engineering, 2012, 59(8), p. 2103-2110.

19. Rahman M. Z. U., Ahamed S. R., Reddy D. V .R. K., Efficient sign based normalized adaptive filtering techniques for cancelation of artifacts in ECG signals: Application to wireless biotelemetry, Signal Processing, 2011, 91, p. 225-239.

20. Rahman M. Z. U., Ahamed S. R., Reddy D. V. R. K., Efficient and simplified adaptive noise cancellers for ECG sensor based remote health monitoring, IEEE Sensors Journal, 2012, 12(3), p. 566-573.

21. Soumya I., Md Zia Ur Rahman., Reddy D. V. R. K., Lay-Ekuakille A., Efficient Block Processing of Long duration Biotelemetric Brain data for Health Care Monitoring, Review of Scientific Instruments, 2015, 86, 035003.

22. Ali H Syed, John Wiley and Sons, Adaptive Filters, New Jersey, USA, 2008.

23. Farhang-Boroujeny B., John Wiley and Sons, Adaptive Filters-Theory and Applications, Chichester, UK, 1998.

24. Eweda E., Comparison of RLS, LMS, and Sign Algorithms for Tracking Randomly Time-Varying Channels, IEEE Transactions on Signal Processing, 1994, 42(11), p. 2937-2944.

25. Park T. H., Youn D. H., Cha I. W., Multiplication-Free Adaptive Digital Filters, Proceedings of IEEE, 1988, 76(5), p. 632-634.

26. Punchalard R., Koseeyaporn J., Wardkein P., Adaptive IIR notch filter using a modified sign algorithm, 2009, Signal Processing, 89, p. 239-243.

27. Dasgupta S., Garnett J.S., Johnson C.R. Jr, Convergence of an Adaptive Filter with Signed Filtered Error, IEEE Transactions on Signal Processing, 1994, 42(4), p. 946-950.

28. Emotiv systems Emotiy Brain Computer Interface Technology, San Francisco, CA USA [Online] Available at: http://emotiv.com (accessed 07/12/2015)

29. Malmivuo J., Plonsey R., Bioelectromagnetism: Principles and Applications of Bioelectric and Biomagnetic Fields, Oxford, U.K.: Oxford University Press, 1995.