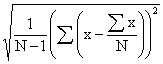Quality control chart for crushed granite concrete
Ewa E. DESMOND 1*, Okafor O. FIDELIS 2
1 Department of Civil Engineering, Cross River University of Technology, Calabar, Nigeria
2 Department of Civil Engineering, University of Nigeria Nsukka, Nigeria
E-mails: desmondewa4sky@gmail.com; fidelis.okafor@unn.edu.ng
* Corresponding author, phone: +234 806 792 8199
Received: February 20, 2016 / Accepted: July 17, 2016 / Published: July 31, 2016
Abstract
A chart for assessing in-situ grade (strength) of concrete, has been developed in this study. Four grades of concrete after the Nigerian General Specification for Roads and bridges (NGSRB)-C20, C25, C30 and C35, is studied at different water-cement ratios for medium and high slump range. The concrete mixes are made from crushed granite rock as coarse aggregate with river sand as fine aggregate. Compression test on specimens are conducted at curing age of 1, 3, 7, 14, 21, 28 and 56 days. Results on concrete workability from slump values, and water-cement ratios revealed that specimens with lower water-cement ratio were less workable but had higher strength, compared to mixes with higher water cement ratio. A simple algorithm using nonlinear regression analysis performed on each experimental data set produced Strength-Age (S-A) curves which were used to establish a quality control chart. The accuracy of these curves were evaluated by computing average absolute error (AAS), the error of estimate (EoE) and the average absolute error of estimate (Abs EoE) for each concrete mix. These were done based on the actual average experimental strengths to measure how close the predicted values are to the experimental data set. The absolute average error of estimate (Abs. EoE) recorded was less than ±10% tolerance zone for concrete works.
Keywords
Concrete grade; Compressive strength; Water-cement ratio; Crushed aggregate; Quality control
Introduction
Arguments on whether concrete mix used in a structure satisfies contract specification are common among stakeholders in the Nigerian construction industry. Collapse of a structure may take place if design strengths is not attained by the structure. In [1] is reported that the compressive strength of structural members of a collapsed 5-storey structure range from 9.30 to 11.2 N/mm2. The poor quality of concrete used led to eventual collapse. In one study, the authors [2] identified low quality materials for construction and low quality concrete as the two major factors responsible for incessant collapse of building in Nigeria. Properties that measure concrete quality include: compressive strength, tensile strength, density, shrinkage, creep, permeability, etc. The compressive test on hardened concrete and the slump test on fresh concrete are the most widely used criteria to assess concrete quality. This is because most other properties are directly or indirectly relate to the compressive strength and workability of concrete. While the compressive strength is conduct on hardened concrete to confirm conformity to strength specifications, slump values monitor the quality of fresh concrete before placement. Factors that influence the compressive strength of concrete are water-cement ratio, cement content, cement and aggregate properties [2, 3].
The grades of concrete for structural purpose and general construction specified by [4] include, C20, C25, C30 and C35. While the numerals represent the minimum cube crushing strength after a 28-day curing period [5]. The routine test by Nigerian codes to assess concrete quality is mainly by conducting compression test on concrete cylinders or cubes.
In reviewing contemporary issues in building collapse and its implications for sustainable development, [7] identified structural failure as the foremost cause of building collapse in Nigeria. When concrete used in a structure does not attain the minimum designed compressive strength, structural failure could occur among other reasons.
In this work, we proposed the use of empirically established concrete strength-age chart as a paradigm tool for quality control of concrete structures. The chart developed is for concrete grades specified by [4], made with crushed granite as coarse aggregate. This chart will serve as a quick guide to assess compliance of concrete used in a structure to the specified grade(s) provided in the contract.
Material and method
Materials used in the study include, Portland cement Type-I, class 32.5R manufactured by the UNITED CEMENT COMPANY OF NIGERIA, UNICEM as binder; Calabar River sand as fine aggregate; crushed granite obtained from a quarry located in Akamkpa LGA of Cross River State, Nigeria, was used as coarse aggregate. The aggregates were prepared in accordance with [8] and [9]. Pipe borne water is used as mixing water for making concrete.
All concrete laboratory works were prepared in the Cross River University of Technology Materials Laboratory. Batching of constituents’ materials were done by weighing and the physical test conducted on the concrete, were slump test to assess workability and compressive strength test. Concrete mixtures adopted for evaluation are shown in Table 1, for concrete of structural purpose and general construction for medium and high slump range as specified by [4].
Table 1. Mix Proportion
|
Grade, N/mm2 |
Designed slump, mm |
Mix ratio |
Water-cement ratio, w/c |
Cement, kg/m3 |
Water, kg/m3 |
Fine aggregate, kg/m3 |
Coarse aggregate, kg/m3 |
|
20 |
30-60 |
1:2.19:2.68 |
0.48 |
350 |
168 |
766 |
937 |
|
60-180 |
1:2.23:2.62 |
0.57 |
350 |
200 |
782 |
918 |
|
|
25 |
30-60 |
1:1.90:2.32 |
0.46 |
400 |
184 |
761 |
929 |
|
60-180 |
1:1.95:2.38 |
0.55 |
400 |
220 |
780 |
952 |
|
|
30 |
30-60 |
1:1.72:2.1 |
0.44 |
450 |
198 |
774 |
946 |
|
60-180 |
1:73:2.11 |
0.50 |
450 |
225 |
778 |
950 |
|
|
35 |
30-60 |
1:1.49:1.89 |
0.44 |
500 |
220 |
743 |
907 |
|
60-180 |
1:1.51:1.84 |
0.48 |
500 |
225 |
755 |
920 |
Workability of fresh concrete was assessed using slump test values carried out in accordance with [10]. The compressive strength of concrete is evaluate as given in Eq.(1):
|
fc = P/A |
(1) |
where fc = compressive strength (N/mm2 or MPa); P = load to failure, N; A = cross-sectional area, mm2.
To determine concrete compressive strengths, 150mm by 150mm concrete cubes were prepared in accordance with [11-13] and [6].
The compressive strengths were determined for 1, 3, 7, 14, 21, 28, and, 56 days curing periods. As required by [4], three (3) specimens were tested for each mix and the average compressive strength found.
Non-linear regression analysis was performed on each experimental data set to produce a strength-age relationship using the Log Function of Microsoft Excel 2016. The flow chart of Figure 1 shows the evolution of concrete strength-age chart.

Figure 1. Flow chart for evolution of concrete strength-age chart
In Nigeria, six test cubes are recommend for testing at curing ages 7 and 28 days; in accordance with [6]. After testing, the 28-day compressive strength should satisfy Eq.(2):
|
facc ≥ fm – 1.645 |
(2) |
where, facc = acceptable compressive strength of concrete, fm = average value of cube strength; S = standard deviation
The specification by [4] also, recommends that the overall average compressive strength and standard deviation is calculated using Equation (3) from the results obtained from the latest forty (40) consecutive sets.
|
S = |
(3) |
where N = Number of cubes tested; x = 28-day compressive strength of 150mm cube in N/mm2; S= Standard deviation in N/mm2.
The standard deviation is computed only when there are at least 40 sets of 3 tests cube for a given concrete mix.
Concrete compressive strength versus age, is related by Eq.4 [2]:
|
ft = A ln(t) + B |
(4) |
where (ft) is the compressive strength at age (t) days and (A) and (B) are constants.
The values of A and B can be evaluated for mixture-specific predicting models.
Results and discussion
Material characteristics
Table 2 shows the chemical composition of the UNICEM Type-I cement used for the study.
Table 2. Composition of cement used
|
CaO |
SiO |
Al2 |
Fe2 |
|
64.34 |
20.79 |
4.51 |
2.64 |
|
|
|
|
|
|
Mg |
SO |
K2 |
Na |
|
1.66 |
1.48 |
1.26 |
0.18 |
The grading curves for both fine and coarse aggregate are presented in Figure 2.
|
(a) River sand |
(b) coarse aggregate |
Figure 2. Particle size distribution curves
Workability of concrete
The results of the slump tests conducted on the different grades of concrete to measure concrete workability at various water cement ratios are summarized in Table 3.
Table 3. Workability of concrete mixes
|
Grade |
Mix ratio |
w/c |
Actual Slump (mm) |
|
20 |
1:2.19:2.68 |
0.48 |
47 |
|
1:2.23:2.62 |
0.57 |
62 |
|
|
25 |
1:1.90:2.32 |
0.46 |
51 |
|
1:1.95:2.38 |
0.55 |
156 |
|
|
30 |
1:1.72:2.1 |
0.44 |
39 |
|
1:73:2.11 |
0.50 |
101 |
|
|
35 |
1:1.49:1.89 |
0.44 |
46 |
|
1:1.51:1.84 |
0.48 |
100 |
Compressive strength of concrete
The results of the compressive strengths and age are presented in Table 4 for all the concrete grades under investigation.
The plots of compressive strengths versus age are presented in Figures 3 to 6. Nonlinear regression models using logarithmic function were fitted into all the experimental data set to produce predicting regression lines as shown.
Table 4. Compressive strength and age for various grades of concrete
|
Age (days) |
Compressive strengths (N/mm2) |
|||||||
|
C20, w/c = 0.48, Slump (30-60mm) |
C20, w/c = 0.57, Slump (60-180mm) |
C25, w/c = 0.46, Slump (30-60mm) |
C25, w/c = 0.55, Slump (60-180mm) |
C30, w/c = 0.44, Slump (30-60mm) |
C30, w/c = 0.50, Slump (60-80mm) |
C35, w/c = 0.44, Slump (30-60mm) |
C35, w/c = 0.45, Slump (60-180mm) |
|
|
1 |
5.34 |
5.29 |
7.50 |
7.03 |
7.86 |
7.47 |
10.61 |
9.33 |
|
3 |
15.04 |
14.63 |
18.07 |
17.73 |
20.32 |
19.40 |
23.30 |
23.11 |
|
7 |
18.13 |
17.82 |
23.08 |
22.58 |
23.04 |
22.72 |
27.82 |
27.48 |
|
14 |
23.37 |
22.84 |
26.08 |
25.09 |
28.56 |
27.43 |
33.36 |
32.16 |
|
21 |
24.12 |
23.90 |
28.68 |
27.81 |
30.65 |
29.79 |
35.13 |
34.55 |
|
28 |
25.69 |
25.06 |
31.14 |
29.18 |
33.11 |
32.17 |
38.43 |
36.91 |
|
56 |
27.04 |
26.26 |
32.68 |
31.20 |
34.19 |
33.06 |
40.33 |
38.02 |
|
(a) Slump(30-60mm) |
b) Slump(60-180mm) |
Figure 3. Strength-Age curve for concrete C20
|
(a) Slump(30-60mm) |
b) Slump(60-180mm) |
Figure 4. Strength-Age curve for concrete C25
Strength predicting models
The corresponding mixture-specific strength-age predicting models for the plots of Figures 3 to 6 are presented in Eq.(5) to (12), where D = age of concrete in hours, σ = compressive strength of concrete.
1. Concrete grade C20:
|
For w/c = 0.48, Slump = (30-60mm): σ = 5.4063·ln(D) + 7.3947, r2 = 0.9583 |
(5) |
|
For w/c = 0.57, Slump = (60-180mm): σ = 5.2659·ln(D) + 7.2992, r2 = 0.9565 |
(6) |
|
(a) Slump(30-60mm) |
b) Slump(60-180mm) |
Figure 5. Strength-Age for concrete C30
|
(a) Slump(30-60mm) |
b) Slump(60-180mm) |
Figure 6. Strength-Age for concrete C35
2. Concrete grade C25:
|
For w/c = 0.46, Slump= (30-60mm): σ = 6.2179ln(D) + 9.6001, r2 = 0.9707 |
(7) |
|
For w/c = 0.55, Slump= (60-180mm): σ = 5.8805ln(D) + 9.4317, r2 = 0.9617 |
(8) |
3. Concrete grade C30:
|
For w/c = 0.44, Slump= (30-60mm): σ = 6.5148ln(D) + 10.420, r2 = 0.9569 |
(9) |
|
For w/c = 0.50, Slump= (60-180mm): σ = 6.3557ln(D) + 9.9706, r2 = 0.9583 |
(10) |
4. Concrete grade C35:
|
For w/c = 0.44, Slump= (30-60mm): σ = 7.3383ln(D) + 12.990, r2 = 0.9721 |
(11) |
|
For w/c = 0.45, Slump= (60-180mm): σ = 7.8115ln(D) + 11.556, r2 = 0.9698 |
(12) |
The properties of cement used for concrete production meets the specification for Ordinary Portland Cement (Type I) [11]. The sand is well graded with a specific gravity of 2.55 and coefficient of uniformity (Cu) of 6.0. The coarse aggregate is also well graded with maximum size of 20 mm and specific gravity of 2.70. The aggregates specific gravity was used in determining total aggregates content during mix design. The slump values for each mix are within design range and increases for each grade with increase in the water cement ratio.
Strength of concrete increases with curing age as is seen in the plots. There were rapid increases within the first few days up to 7 days as hydration of cement progresses. This was followed by gradual increment in strength up to 56 days, this trend agrees with [11]. Concrete mixes with lower water-cement ratios (lower slump values), show higher strength compared to mixes with higher water-cement ratios. This trend agrees with [14] and [15].
The predicting models are mixture specific; implying they can be used to predict the compressive strength of concrete with the same mixture requirements. Each model has a coefficient of determination (R2) value greater than 0.95, indicating closeness with experimental strengths; since the R2 is the fraction of the total squared error that is explained by the model with desirable value approaching 1. An R2 value of 0.95 signifies a good predicting model. The novelty of this work is shown in Figure 7, which is a comparative presentation of the models of Equations (4-11), covering concrete grades 20-35N/mm2.
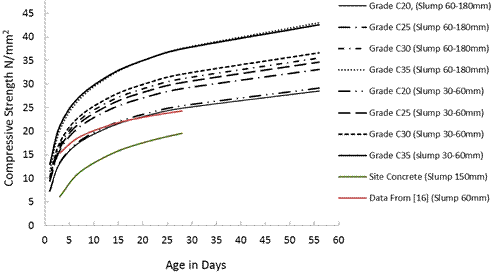
Figure 7. strength-age quality control chart for concrete grades made with crushed granite
This strength-age envelop could be used as a quality control chart to determine a particular concrete grade being used on site. Concrete mix delivered to site by a contractor could be collected and prepared in accordance with [3,8 and 9]. Nonlinear regression analysis is then carried out on the results to develop a mixture-specific strength-age curve.
This curve is then superimposed on Figure 7. By interpolation, the probable grade of concrete being used on site can be estimated. As shown in Figure 7, the new curve for a given Site Concrete (1:2:4, 0.50 mix with 150mm slump value) fell far below the envelope, the concrete grade may not be accepted as C20. Similarly, using the data from [16], with a mix ratio of 1:2:4 and with slump value of 60mm for rapid strength cement (Dangote 3X), the grade of concrete could be estimated to lie within the envelope of grade C20. Other similar concrete grades can be estimated by using the chart.
Conclusions
Nonlinear regression curves were successfully fitted into strength-age data of different concrete mixes to form a quality control chart. The coefficient of determination of each curve was greater than 0.95 and their accuracy was determined by evaluating the average absolute error (AAS), the error of estimate (EoE) and the average absolute error of estimate (Abs EoE) for each concrete mix. The absolute average error of estimate (Abs. EoE) recorded was within ±10% tolerance zone for concrete works. The concrete grade used at a construction site can be estimated by establishing a strength-age curve similar to those in the chart and thereafter, super-imposed on the already established chart.
References
5. Falade F. A., Iheonu E. E., Dede S., Sulymon N. A., Egege C.C, Mozea M. N., Collapse of Buildings in Nigeria: Technical Report on the collapse at Adenubi Close, Building and Road Research Institute Report, No. 23, 2011.
6. Metwally abd allah Abd elaty, Compressive strength prediction of Portland Cement Concrete with age using a new model, Housing and Building Research Center Journal, 2014, 10, p. 145-155.
7. Zongjin L., Advanced Concrete Technology 1st edition, New Jersey, John Wiley and Sons Inc, 2011.
8. General Specifications for Roads and Bridges, Government of the Federal Republic of Nigeria, 1997.
9. Kazeem K. A, Wasiu O. A., Idris A. A., Determination of appropriate mix ratios for concrete grades using Nigerian Portland-limestone grades 32.5 and 42.5, Leonardo Electronic Journal of Practices and Technologies, 2015, 14(26), p. 79-88.
10. BS 1881-108 ‘Testing of Concrete’ Part 108: Method for making test cubes from fresh concrete, British Standards Institution, London, 1983.
11. Abimbola O., Windapo, James O. Rotimi, Contemporary Issues in Building Collapse and Its Implications for Sustainable Development, Buildings, 2012, 2, p. 283-299.
12. BS 812-105-2 ‘Testing Aggregate. Method for determination of particle size’, British Standards Institution, London, 1990.
13. BS EN12620 ‘Specification for aggregates from natural sources for concrete’, British Standards Institution, London, 2002.
14. ASTM C143/C143M-12: ‘Standard Test Method for Slump of Hydraulic-Cement Concrete’. ASTM International, Pennsylvania, 2014.
15. ASTM C31/C31M ‘Practice for Making and Curing Concrete Test Specimens in the Field’. ASTM International, Pennsylvania, 2015.
16. ASTM C39/C39M - 05 ‘Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens’. ASTM International, Pennsylvania, 2005.
17. ASTM C-511: ‘Specification for Moist Cabinets, Moist Rooms, and Water Storage Tanks Used in the Testing of Hydraulic Cements and Concretes’. ASTM International, Pennsylvania, 2013.
18. Neville A. M., Properties of Concrete, Pearson Education Limited, Edinburgh Gate, England. 5th Edition, 2011, p. 304-305.
19. Nyiutsa S. A., Aondowase J. S., Ameh P. A., Josephat C. E., Paul T. A., Effect of Water-Cement Ratio on the Compressive Strength of gravel - crushed over burnt bricks concrete, Civil and Environmental Research, 2013, 3(4), p. 74-81.
20. Gideon O. B., Anthony N. E., Chioma E., Joshua J., Oluwaleke O., Tajudeen O., Assessment of Compressive Strength of Concrete Produced from Different Brands of Portland Cement, Civil and Environmental Research, 2015, 7(8), p. 31-38.