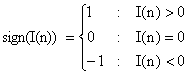Engineering, Environment
Efficient noise cancellers for ECG signal enhancement for telecardiology applications
Nagesh MANTRAVADI1, Svav PRASAD2, Muhammad Zia Ur RAHMAN3*
1& 2Department of Electronics and Communication Engineering, Lingaya’s University, Faridabad-121001, Haryana, India
3Department of Electronics and Communication Engineering, KKR & KSR Institute of Technology, Pratipadu Road, Vinjanampadu-522017, Guntur, A.P., India
Emails: 1nagesmLU@gmail.com, 2prasad.svav@gmail.com, *3mdzr55@gmail.com
*Corresponding Author, Phone: +91 -9440712707
Received: July 13, 2016 / Accepted: December 18, 2016 / Published: December 30, 2016
Abstract
In this paper some effective noise cancellers were proposed using the variants of Least Mean Fourth (LMF) Algorithm to remove the artifacts that occur during the acquisition stage of an ECG signal. In order to accelerate the performance of the LMF algorithm we introduce data normalization in weight update process. This results two variants of LMF algorithm, called normalized LMF (NLMF) and global NLMF (GNLMF) algorithms. Further, to minimize their computational complexity and improve convergence characteristics, tracking ability, filtering capability we apply signum and block processing on the two versions of normalized algorithms. Both the two treatments results six more algorithms. Using these algorithms we develop various adaptive noise cancellers (ANCs). These ANCs are tested with the help of standard MIT-BIH arrhythmia database for various records. The Signal to noise ratio, Excess Mean Square Error and misadjustment are taken as performances measures to analyze the performance of proposed methods. These ANCs exhibit improved performance over the LMF based ANC.
Keywords
Artifacts; ECG Signal; Higher order filters; Noise cancellation; Telecardiology
Introduction
Bio-telemetry basically involves transmission of biomedical information and it is generally employed in ambulatory health care. Any physiological information can be transmitted over the telemetry link provided the information is suitably transformed into electrical form by overcoming the effects of various artifacts. It has been gaining intensive response from the medical community and from the public owing to the recent trends in modern day communication and in handling the data right from the sophisticated acquisition systems to efficient encoding techniques. Out of the various possibilities we have chosen the cardiac signal, due to its importance in controlling the premature deaths. As per the report of World Health Organization (WHO) mortality rate due to the heart problems is 37% [1]. Remote diagnosis helps to reduce the damage to the heart. With the advent of ease of use acquisition systems and due to the vital information that is available, electrocardiography (ECG) units are most commonly observed in health care units. It helps to identify the abnormalities of heart commonly known as arrhythmia. But like any other signal the ECG is generally affected by the artifacts during the acquisition. Minimizing the artifacts is necessary to identify the tiny features of actual signal. It can be done through either adaptive filtering techniques or non adaptive techniques. But the advantage of adaptive filter type lies in their ability to change weights according to the dynamic signal characteristics.
Considerable amount of work is done in denoising the ECG signals using both the adaptive and non adaptive techniques. Saurab Paul et.al in [2] proposed an EMD based denoising and QRS detection technique. Here the low frequency noise is removed by using the slope minimization technique and high frequency noise is removed by discarding the lower order IMF’s. Similarly a multi channel model is proposed in [3] to evaluate the performance of the algorithms. In [4] an adaptive wavelet technique has been proposed to remove the noise. The wiener filter along with dyadic stationary wavelet transform has been used in this technique. In [5] also authors used the DWT approach with sym5 as basis function for removing noise and extracting the features of the ECG signal. In general notch filters were used to remove the predefined harmonics but it has certain limitations. In [6] an adaptive tunable notch filter was proposed to remove the PLI, in [7] an adaptive canceller that tracks the deviation from the predefined frequency using PLL is proposed to remove the noise and in [8] a weighted averaging method is to minimize the noise is proposed. In addition to the non adaptive and adaptive techniques the least mean square algorithm was also used independently in removing the noise from the ECG signal. In [9] Rahman et.al proposed a time-frequency approach to leaky adaptive noise cancellers. Similarly, in [10] the Least Mean Square based variants have been used to remove the artifacts. All the above are some of the examples of the vast techniques proposed to denoise the ECG signal. The main aim of this work is to develop some computationally effective and reliable noise cancellers.
In our present work we would like to use the Least Mean Fourth algorithm introduced by Eugene Walach et.al [11], due to its faster convergence and better MSE at low SNR conditions for noise cancellation in ECG signal. But LMF itself has some disadvantages in [12] Nascimento et.al have shown that the LMF is not mean square stable when the input regressor is getting unbounded and there will be a non zero probability of divergence when the input regressor is having an infinite support. In order to overcome these drawbacks of LMF similar to normalized version of LMS the normalized versions to LMF have been proposed. In [13] the normalization is done by using the squared first order norm. While in [14] normalization is done by means of fourth power of regressor (NLMF). The stability of these algorithms is still dependent on the input variance and noise in weights. ECG signal in general will often contain the zero or negligible values and these two algorithms will be unstable in this scenario. To overcome it in the normalized versions a small constant is added to retain the stability of the algorithm. In [15] Eweda Eweda has proposed a stabilized version of LMF called Global stabilized Normalized Least Mean Fourth (GNLMF) algorithm. This algorithm was found to exhibit stability to all signal statistics, signal power and weight initialization [16]. The stability and convergence properties can be improved by using the LMF for filtering ECG signal now it is necessary to reduce the complexity of the algorithm to meet the timing requirements. To address it Rahman et.al in [10] used the normalized sign based algorithms. Similarly block based versions are also used here to further the complexity.
To cope up with the problems associated with conventional noise cancellers in this paper we propose to develop various noise cancellers to enhance ECG signals using higher order algorithms. The algorithms so obtained by using the sign and block based versions are Normalized sign regressor LMF with increase stability (NSRLMF), Global stable Normalized sign regressor algorithm (GNSRLMF), block based normalized LMF with increased stability (BBNLMF), block based sign regressor normalized LMF with increased stability (BBNSRLMF), block based globally stable normalized LMF (BBGNLMF) and block based globally stable normalized sign regressor LMF (BBGNSRLMF).
Material and method
In this section we present various algorithms to develop various ANCs to clean ECG signals for recovering the signal buried in artifacts. The influence of these artifacts can be seen in terms of degraded signal morphology and spurious voltages. As the voltage is one of the factors in detecting the arrhythmia we need to remove the artifacts. In this section we aim at removing these artifacts from the ECG signal using the LMF algorithm and its variants. The basic working of an adaptive filter can be seen in [17], where the authors used two fundamental adaptive filtering structures. In which former takes the noise as reference and the later takes a clean signal itself as a reference. Here we would like to use the filter with noise as reference because from the conclusions drawn by Thakoor et.al [17] it is clear that providing a signal as reference will not yield correct results in case of changing signal shape. The structure taken for filtering is as shown in Figure 1.
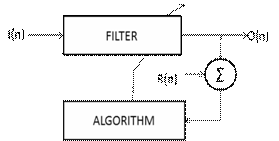
Figure 1. Basic adaptive noise canceller structure
Let us consider Z(n)=[z1,z2, .....zn]T be the weight vector of adaptive filter which we are going to use to extract the signal buried in noise. Let I(n)=[I1,I2,.....In]T be the input to this adaptive filter and R(n) is the vector holding the actual signal data. Let the noise added to this R(n) be denoted as v1, and the reference input I(n) is assumed to be correlated with the noise that corrupted the signal. Let O(n) be the output of the filter due to I(n). The error can be given as d(n) = O(n)-(R(n)+v1) where O(n) = I(n)*Z(n). Now by minimizing the term E[d4(n)] with respect to the weight Z(n) will yield the weight update equation for Least Mean Fourth Algorithm. Therefore, the weight update equation for the LMF filter is [11]:
|
|
(1) |
Based on the structure shown in Figure 1 we develop nine ANC structures. In these ANCs all the blocks, inputs and parameters are same, except algorithm used. To improve the performance of LMF algorithm we propose various versions of LMF based algorithms.
These are discussed in this section. Using these various algorithms, by replacing the all these algorithms we test the performance of various ANCs. The nine algorithms used to develop nine ANCs for ECG enhancement are: LMF, NLMF, BBNLMF, NSRLMF, BBNSRLMF, GNLMF, BBGNLMF, GNSRLMF and BBGNSRLMF algorithms.
From the earlier work it is clear that the LMF outperform LMS at low SNR and in non Gaussian environment. But the stability of the algorithm depends on the input signal power, how initial weights are chosen. The algorithm converges faster at low SNR while the rate of convergence reduces at high SNR which is not a desirable feature. In order to overcome these drawbacks of LMF, the normalized versions were introduced. The idea behind these normalization techniques is to control the step size by introducing the even ordered power of the data. As the step size is known to control the convergence and the error its normalization is justified. The weight update equation of the normalized version NLMF can be written [14]:
|
|
(2) |
But the above algorithm is not completely independent to signal power, so by considering the results in [16] the equation for the new normalized LMF called Global stabilized Normalized Least Mean Fourth algorithm (GNLMF) can be written as [15]:
|
|
(3) |
The constant δ is added here to overcome the instability that arises when the signal contains zero valued samples. The above algorithm is stable against all signal statistics, noise power and signal power. In addition to stability the computation time is known to be an important issue in any algorithmic design. Special focus need to be put in it if we were going to implement them in portable devices to make real time monitoring. An algorithm with highest accuracy but with larger computational time is not a desirable feature. To overcome this signum based versions were used in [10]. These basically fall into three categories wherein first type the signal is clipped called signed regressor, in second type error is clipped, it is called sign algorithm and finally both are clipped called the sign-sign algorithm. The signum function can be mathematically given as:
|
|
(4) |
The major advantage of sign regressor operation (SRO) is it requires only one multiplication in the computation of µd3(n)I(n) in the weight update recursion. Hence, the number of multiplications in SRO based algorithm is independent of filter length. This seems to be major advantage of this operation [10]. Now by applying this to the above equations, we get two new variants namely Normalized Sign regressor LMF (NSRLMF) and Global Normalized Signed Regressor LMF (GNSRLMF). The equations can be written as:
|
|
(5) |
|
|
(6) |
But in order to reduce the computational complexity we are going to use the block based versions. In these block based versions the step size parameter gets normalized with maximum data value of the input vector instead of all the elements of input data vector. Due to this, in the denominator of the weight update operation only one multiplication is need. By doing so, in denominator we are reducing L-1 multiplications. The weight update for block based versions BBNLMF, BBNSRLMF, BBGNLMF and BBGNSRLMF can be written:
|
|
(7) |
|
|
(8) |
|
|
(9) |
|
|
(10) |
These variants are found to be giving performance nearer to the original counterparts, with reduced number of multiplications. Therefore, based on SRO and block based normalization we are able to reduced the number of multiplications in the numerator as well as denominator of the weight update equation. Hence, based on this discussion with reference to computational complexity of the algorithm BBNSRLMF and BBGNSRLMF algorithms are better candidates for developing ANCs to enhance ECG signals.
Results and Discussion
The performance of the various proposed noise cancellers for ECG enhancement is discussed in this section. Based on the algorithms discussed in the previous sections we have developed of the proposed algorithms we have used MIT-BIH arrhythmia database. Among the various datasets we have taken 100, 105, 108, 203, 228 records each with a length of 4000 samples. Here the window length and block length are taken as 5, also the constant δ is taken as 0.1. In order to compare the performance of these versions we have used Excess Mean Square Error (EMSE), Misadjustment (MSD) and signal to noise ratio improvement (SNRI) as performance measures. Figures 2-5 illustrates the performance of the proposed implementations in filtering the artifacts.
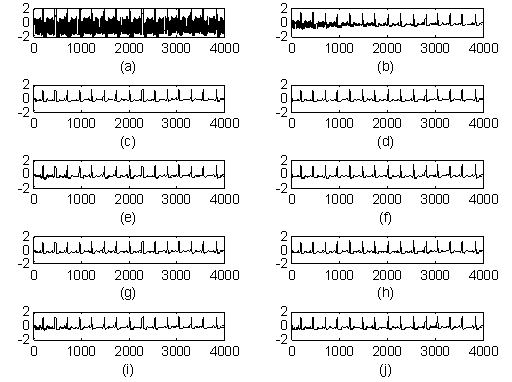
Figure 2. Power Line Interference Cancellation a) Contaminated ECG signal, ECG
signal filtered with b) LMF, c)NLMF, d)BBNLMF, e)NSRLMF,
f)BBNSRLMF,
g) GNLMF, h) BBGNLMF, i) GNSRLMF and j) BBGNSRLMF algorithms

Figure 3. Base Line Wander Cancellation a) Contaminated ECG
signal, ECG signal filtered with b) LMF, c)NLMF, d)BBNLMF, e)NSRLMF,
f)BBNSRLMF, g) GNLMF,
h) BBGNLMF, i) GNSRLMF and j) BBGNSRLMF algorithms

Figure 4. Muscle artifact Cancellation a) Contaminated ECG
signal, ECG signal filtered with b) LMF, c)NLMF, d)BBNLMF, e)NSRLMF,
f)BBNSRLMF, g) GNLMF, h) BBGNLMF,
i) GNSRLMF and j) BBGNSRLMF algorithms
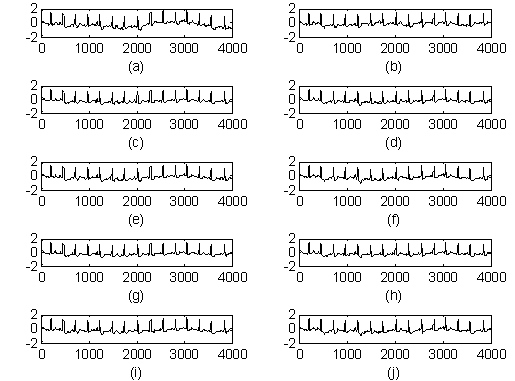
Figure 5. Motion Artifact Cancellation a) Contaminated ECG
signal, ECG signal filtered with b) LMF, c)NLMF, d)BBNLMF, e)NSRLMF, f)BBNSRLMF,
g) GNLMF, h) BBGNLMF,
i) GNSRLMF and f) BBGNSRLMF algorithms
Table 1, Table 2 and Table 3 shows the performance of the proposed noise cancellers in terms of SNRI, EMSE and MSD.
Table 1. SNRI performance of various algorithms for ECG enhancement
|
Noise Type |
Record Number |
LMF |
NLMF |
BBNLMF |
NSRLMF |
BBNSRLMF |
GNLMF |
BBGNLMF |
GNSRLMF |
BBGNSRLMF |
|
PLI |
100 |
8.12 |
10.96 |
12.66 |
9.95 |
10.52 |
14.94 |
16.25 |
13.90 |
16.00 |
|
105 |
8.35 |
11.47 |
13.79 |
10.95 |
11.98 |
14.67 |
16.78 |
13.63 |
15.41 |
|
|
108 |
8.67 |
10.30 |
13.76 |
9.62 |
10.76 |
14.96 |
16.30 |
13.91 |
15.98 |
|
|
203 |
7.45 |
9.88 |
13.50 |
9.13 |
10.85 |
14.65 |
16.98 |
13.42 |
15.82 |
|
|
228 |
8.17 |
10.40 |
13.36 |
8.95 |
10.03 |
14.93 |
16.99 |
13.02 |
15.79 |
|
|
BW |
100 |
4.44 |
11.89 |
12.66 |
9.88 |
10.96 |
14.07 |
15.91 |
13.86 |
13.12 |
|
105 |
4.98 |
11.29 |
13.78 |
9.96 |
10.76 |
14.65 |
15.21 |
13.13 |
12.29 |
|
|
108 |
3.61 |
10.45 |
11.76 |
9.40 |
10.94 |
14.06 |
15.28 |
13.48 |
12.59 |
|
|
203 |
3.26 |
11.00 |
11.50 |
9.84 |
10.45 |
14.19 |
15.82 |
13.29 |
12.22 |
|
|
228 |
3.25 |
10.28 |
12.36 |
9.98 |
10.84 |
14.82 |
15.26 |
13.48 |
12.32 |
|
|
MA |
100 |
4.75 |
12.76 |
13.48 |
10.53 |
11.46 |
14.27 |
15.23 |
13.69 |
14.31 |
|
105 |
5.98 |
12.32 |
13.72 |
10.74 |
11.30 |
14.16 |
15.12 |
13.80 |
14.27 |
|
|
108 |
5.55 |
12.84 |
13.01 |
10.52 |
11.80 |
14.30 |
15.94 |
13.76 |
14.27 |
|
|
203 |
5.53 |
12.71 |
13.97 |
10.62 |
11.04 |
14.98 |
15.63 |
13.40 |
14.07 |
|
|
228 |
5.49 |
12.21 |
13.53 |
10.88 |
11.43 |
14.10 |
15.09 |
13.03 |
14.44 |
|
|
EM |
100 |
4.68 |
11.57 |
12.81 |
10.71 |
11.93 |
14.99 |
15.57 |
13.82 |
14.05 |
|
105 |
5.11 |
11.95 |
12.63 |
10.29 |
11.97 |
14.90 |
15.35 |
13.21 |
14.16 |
|
|
108 |
5.21 |
11.85 |
12.20 |
10.20 |
11.60 |
14.16 |
15.29 |
13.72 |
14.24 |
|
|
203 |
5.75 |
11.20 |
12.62 |
10.46 |
11.59 |
14.21 |
15.64 |
13.54 |
14.25 |
|
|
228 |
3.72 |
11.03 |
12.60 |
10.38 |
11.19 |
14.57 |
15.18 |
13.73 |
14.81 |
Table 2. EMSE Performance of various algorithms for ECG enhancement
|
Noise Type |
Record Number |
LMF |
NLMF |
BBNLMF |
NSRLMF |
BBNSRLMF |
GNLMF |
BBGNLMF |
GNSRLMF |
BBGNSRLMF |
|
PLI |
100 |
-20.94 |
-31.15 |
-33.31 |
-28.61 |
-30.72 |
-35.44 |
-38.58 |
-32.97 |
-35.81 |
|
105 |
-22.83 |
-31.76 |
-33.94 |
-29.21 |
-30.41 |
-38.13 |
-40.59 |
-36.58 |
-38.65 |
|
|
108 |
-21.55 |
-31.85 |
-33.05 |
-29.46 |
-30.42 |
-35.66 |
-38.77 |
-33.31 |
-36.20 |
|
|
203 |
-22.54 |
-31.76 |
-33.93 |
-29.26 |
-30.74 |
-33.33 |
-36.23 |
-30.25 |
-33.02 |
|
|
228 |
-22.58 |
-32.13 |
-33.42 |
-29.66 |
-31.11 |
-36.20 |
-38.76 |
-34.03 |
-36.89 |
|
|
Average |
-22.09 |
-31.73 |
-33.53 |
-29.24 |
-30.68 |
-35.75 |
-38.59 |
-33.43 |
-36.11 |
|
|
BW |
100 |
-12.15 |
-11.35 |
-12.23 |
-10.09 |
-11.00 |
-11.48 |
-12.38 |
-10.12 |
-11.94 |
|
105 |
-12.44 |
-12.56 |
-13.34 |
-10.97 |
-11.19 |
-14.90 |
-15.34 |
-12.26 |
-13.11 |
|
|
108 |
-12.47 |
-11.85 |
-12.45 |
-10.20 |
-11.08 |
-11.55 |
-12.40 |
-10.24 |
-11.08 |
|
|
203 |
-10.96 |
-10.67 |
-11.14 |
-9.42 |
-10.79 |
-10.83 |
-11.92 |
-9.47 |
-10.76 |
|
|
228 |
-13.62 |
-12.86 |
-13.69 |
-11.09 |
-12.15 |
-12.93 |
-13.78 |
-11.34 |
-12.08 |
|
|
Average |
-12.33 |
-11.86 |
-12.57 |
-10.35 |
-11.24 |
-12.34 |
-13.01 |
-10.69 |
-11.79 |
|
|
MA |
100 |
-13.11 |
-13.98 |
-14.89 |
-11.17 |
-12.39 |
-14.24 |
-15.10 |
-11.78 |
-12.36 |
|
105 |
-13.45 |
-15.50 |
-16.08 |
-12.15 |
-13.82 |
-15.62 |
-16.16 |
-12.16 |
-13.85 |
|
|
108 |
-12.73 |
-14.43 |
-15.97 |
-11.24 |
-12.32 |
-14.05 |
-15.87 |
-12.01 |
-13.27 |
|
|
203 |
-12.61 |
-14.57 |
-15.14 |
-11.46 |
-12.20 |
-13.73 |
-14.56 |
-11.32 |
-12.79 |
|
|
228 |
-14.43 |
-16.25 |
-17.94 |
-12.02 |
-13.79 |
-16.16 |
-17.98 |
-13.26 |
-14.77 |
|
|
Average |
-13.27 |
-14.95 |
-16.01 |
-11.61 |
-12.90 |
-14.76 |
-15.94 |
-12.10 |
-13.41 |
|
|
EM |
100 |
-11.80 |
-11.92 |
-12.84 |
-10.25 |
-11.36 |
-12.01 |
-13.97 |
-10.41 |
-11.34 |
|
105 |
-11.72 |
-13.45 |
-14.19 |
-11.31 |
-12.46 |
-13.51 |
-14.16 |
-11.88 |
-12.39 |
|
|
108 |
-11.90 |
-12.62 |
-13.14 |
-10.52 |
-11.31 |
-12.10 |
-13.05 |
-10.81 |
-11.30 |
|
|
203 |
-9.24 |
-11.22 |
-12.18 |
-9.32 |
-10.08 |
-10.80 |
-11.72 |
-9.59 |
-10.63 |
|
|
228 |
-13.40 |
-13.74 |
-14.64 |
-11.88 |
-12.82 |
-13.79 |
-14.71 |
-12.25 |
-13.70 |
|
|
Average |
-11.61 |
-12.59 |
-13.40 |
-10.66 |
-11.61 |
-12.44 |
-13.52 |
-10.99 |
-11.87 |
Table 3. MSD Performance of various algorithms for ECG enhancement
|
Noise Type |
Record Number |
LMF |
NLMF |
BBNLMF |
NSRLMF |
BBNSRLMF |
GNLMF |
BBGNLMF |
GNSRLMF |
BBGNSRLMF |
|
PLI |
100 |
0.0711 |
0.0141 |
0.0058 |
0.0406 |
0.0132 |
0.0105 |
0.0022 |
0.0200 |
0.0038 |
|
105 |
0.0430 |
0.0111 |
0.0046 |
0.0394 |
0.0104 |
0.0095 |
0.0021 |
0.0187 |
0.0038 |
|
|
108 |
0.0724 |
0.0129 |
0.0054 |
0.0470 |
0.0117 |
0.0109 |
0.0022 |
0.0197 |
0.0038 |
|
|
203 |
0.0204 |
0.0078 |
0.0026 |
0.0032 |
0.0058 |
0.0092 |
0.0018 |
0.0192 |
0.0036 |
|
|
228 |
0.0515 |
0.0146 |
0.0062 |
0.0393 |
0.0138 |
0.0107 |
0.0024 |
0.0207 |
0.0040 |
|
|
Average |
0.0516 |
0.0121 |
0.0049 |
0.0339 |
0.0109 |
0.0101 |
0.0021 |
0.0196 |
0.0038 |
|
|
BW |
100 |
0.4829 |
0.5727 |
0.5577 |
0.7594 |
0.7446 |
0.5536 |
0.5409 |
0.7703 |
0.7388 |
|
105 |
0.4030 |
0.4009 |
0.3816 |
0.6583 |
0.5498 |
0.3929 |
0.3527 |
0.6700 |
0.5144 |
|
|
108 |
0.4960 |
0.5879 |
0.5364 |
0.8049 |
0.7834 |
0.5944 |
0.5741 |
0.8061 |
0.7766 |
|
|
203 |
0.3842 |
0.3727 |
0.3298 |
0.4038 |
0.4405 |
0.3923 |
0.3185 |
0.6456 |
0.4354 |
|
|
228 |
0.4630 |
0.5447 |
0.5238 |
0.7771 |
0.7873 |
0.5341 |
0.5152 |
0.7887 |
0.7427 |
|
|
Average |
0.4458 |
0.4957 |
0.4658 |
0.6807 |
0.6611 |
0.4934 |
0.4602 |
0.7361 |
0.6415 |
|
|
MA |
100 |
0.3667 |
0.3102 |
0.3038 |
0.5522 |
0.5808 |
0.2956 |
0.2866 |
0.5558 |
0.5050 |
|
105 |
0.4025 |
0.2136 |
0.1939 |
0.4520 |
0.4194 |
0.2095 |
0.1887 |
0.4496 |
0.4184 |
|
|
108 |
0.4579 |
0.3291 |
0.2960 |
0.6057 |
0.6168 |
0.3362 |
0.3231 |
0.6122 |
0.5163 |
|
|
203 |
0.6090 |
0.1867 |
0.1345 |
0.2924 |
0.2753 |
0.2137 |
0.1633 |
0.4043 |
0.2845 |
|
|
228 |
0.3262 |
0.2578 |
0.2402 |
0.5324 |
0.6356 |
0.2555 |
0.2448 |
0.5351 |
0.4782 |
|
|
Average |
0.4324 |
0.2594 |
0.2336 |
0.4869 |
0.5055 |
0.2621 |
0.2413 |
0.5114 |
0.4404 |
|
|
EM |
100 |
0.5319 |
0.4972 |
0.4881 |
0.6991 |
0.7171 |
0.4833 |
0.4790 |
0.7030 |
0.6915 |
|
105 |
0.5936 |
0.3302 |
0.3110 |
0.6180 |
0.4090 |
0.3326 |
0.3068 |
0.6281 |
0.4465 |
|
|
108 |
0.5792 |
0.5013 |
0.4486 |
0.7641 |
0.7286 |
0.5123 |
0.5059 |
0.7666 |
0.6809 |
|
|
203 |
0.6719 |
0.3698 |
0.2911 |
0.4766 |
0.4500 |
0.4112 |
0.3203 |
0.6650 |
0.4230 |
|
|
228 |
0.4929 |
0.4377 |
0.4279 |
0.6664 |
0.6567 |
0.4308 |
0.4232 |
0.6849 |
0.6028 |
|
|
Average |
0.5379 |
0.4272 |
0.3933 |
0.6448 |
0.5922 |
0.4304 |
0.4070 |
0.6895 |
0.5689 |
All the artifacts except power line interference (PLI) i.e., base line wander (BW), Muscle artifacts (MA) and Electrode motion (EM) artifact are taken from the MIT-BIH Normal Sinus Rhythm Database (NSTDB). These are recorded from 18 subjects at a sample rate of 128 Hz who have no noticed arrhythmias. Similarly the PLI is generated with 1mv in amplitude. Simulations results correspond to data 105 are shown in this paper.
Based on the analysis presented with reference to computational complexity BBNSRLMF and BBGNSRLMF algorithms are better candidates for developing ANCs to enhance ECG signals. Now by examining the experimental results presented in Figures 2 to 5 and Tables 1 to 3, we conclude which algorithm is a best candidate for ANC development with reference to SNR, EMSE and MSD.
Power Line Interference Cancellation
In this experiment the noisy ECG signal is given as input the ANC as I(n), a synthetic noise with a frequency of 60Hz is given as a reference signal R(n) as shown in Figure 1. The simulation results are shown in Figure 2. The SNRI values achieved by ANCs based on LMF, NLMF, BBNLMF, NSRLMF, BBNSRLMF, GNLMF, BBGNLMF, GNSRLMF and BBGNSRLMF are 8.3485dBs, 11.4725dBs, 13.7868dBs, 10.9466dBs, 11.9814dBs, 14.6712dBs, 16.7812dBs, 13.6284dBs and 15.4091dBs respectively. From these values by keeping computational complexity in consideration we can say that BBGNSRLMF based ANC outperforms in the enhancement process of ECG signal. This also evident by its EMSE, MSD values -38.6457dBs and 0.0038 respectively.
Base line Wander Cancellation
In this experiment the noisy ECG signal is given as input the ANC as I(n), a reference BW artifact is given as a reference signal R(n) as shown in Figure 1. The simulation results are shown in Figure 3. Similarly the SNR, EMSE, MSD can be observed in the Tables 1, 2 and 3. The SNRI values achieved by ANCs based on LMF, NLMF, BBNLMF, NSRLMF, BBNSRLMF, GNLMF, BBGNLMF, GNSRLMF and BBGNSRLMF are 4.9814dBs, 11.2891dBs, 13.7829dBs, 9.9608dBs, 10.7641dBs, 14.6536dBs, 15.2112dBs, 13.1317dBs and 12.2850dBs respectively. From these values by keeping computational complexity in consideration we can say that BBGNSRLMF based ANC outperforms in the enhancement process of ECG signal. This also evident by its EMSE, MSD values -13.1133dBs and 0.5144 respectively.
Muscle artifact cancellation
In this experiment the noisy ECG signal is given as input the ANC as I(n), a muscle artifact is given as reference signal R(n) as shown in Figure 1. The simulation results are shown in Figure 4. The SNRI values achieved by ANCs based on LMF, NLMF, BBNLMF, NSRLMF, BBNSRLMF, GNLMF, BBGNLMF, GNSRLMF and BBGNSRLMF are 5.9820dBs, 12.3248dBs, 13.7158dBs, 10.7392dBs, 11.3007dBs, 14.1589dBs, 15.1198dBs, 13.7969dBs and 14.2742dBs respectively. From these values by keeping computational complexity in consideration we can say that BBGNSRLMF based ANC outperforms in the enhancement process of ECG signal. This also evident by its EMSE, MSD values -13.8460dBs and 0.4184 respectively.
Motion artifact Cancellation
In this experiment the noisy ECG signal is given as input the ANC as I(n), a motion artifact is given as reference signal R(n) as shown in Figure 1. The simulation results are shown in Figure 4. The SNRI values achieved by ANCs based on LMF, NLMF, BBNLMF, NSRLMF, BBNSRLMF, GNLMF, BBGNLMF, GNSRLMF and BBGNSRLMF are 5.1127dBs, 11.9500dBs, 12.6323dBs, 10.2890dBs, 11.9696dBs, 14.8975dBs, 15.3474dBs, 13.2121dBs and 14.1625dBs respectively. From these values by keeping computational complexity in consideration we can say that BBGNSRLMF based ANC outperforms in the enhancement process of ECG signal. This also evident by its EMSE, MSD values -12.3940dBs and 0.4465 respectively.
Conclusions
In our work we proposed some noise cancellation techniques to filter the biomedical data in a way suitable to telemetry applications using the Least mean Fourth algorithm variants. The LMF along with its variants NLMF, GNLMF and their signed, block based versions NSRLMF, GNSRLMF, BBNLMF, BBGNLMF, BBNSRLMF, BBGNSRLMF are used to develop ANCs to enhance ECG signals in clinical environment. All the ANCs are tested on real ECG signals obtained from MIT-BIH database. The performance of these ANCs are measured and analyzed. Based on the experimental results presented in Figures 2 to 5 and Tables 1 to 3 it is found that, among all the ANCs BBGNSRLMF based ANC performs better. This ANC has lower computational complexity due to sign regressor operation involved and block based normalization. The performance measures are also very close to BBGNLMF which has much complexity. Hence, this ANC can be used for the practical realization of health care monitoring systems.
References
1. Global Status Report on Non communicable Diseases 2014 by WHO available at http://www.who.int/nmh/publications/ncd-status-report-2014/en/.
2. Saurabh Pal., MadhuchhandaMitra, Empirical mode decomposition based ECG enhancement and QRS detection, Computers in Biology and Medicine, 2011, p. 83-92.
3. Sameni R., Clifford G. D., Jutten C., Shamsollahi M. B., Multichannel ECG and Noise Modeling: Application to Maternal and Fetal ECG Signals, EURASIP Journal on Advances in Signal Processing , 2007.
4. Smital L., Vitek M., Kozumplik J., Provaznik I., Adaptive Wavelet Wiener Filtering of ECG Signals, IEEE Transactions on Biomedical Engineering, 2013, 60(2), p. 437-445.
5. Lin H. Y., Liang S. Y., Ho Y.L., Lin Y. H., Ma H. P., Discrete-wavelet-transform-based noise removal and feature extraction for ECG signals, Health com, 2013, p. 351-361.
6. Verm A. R., Singh Y., Adaptive Tunable Notch Filter for ECG Signal Enhancement, Procedia Computer Science, 2015, 57, p. 332 – 337.
7. Martens S. M. M., Mischi M., GuidOei S., Bergmans J. W. M., An Improved Adaptive Power Line Interference Canceller for Electrocardiography, IEEE Transactions on Biomedical Engineering, 2006, 53(11), p. 2220-2231.
8. Momot A, Methods of weighted averaging of ECG signals using Bayesian inference and criterion function minimization, Biomedical Signal Processing and Control, 2009, 4, p. 162–169.
9. Rahman M.Z.U., Karthik G.V.S., Fathima S.Y., Lay-Ekuakille A., An efficient cardiac signal enhancement using time–frequency realization of leaky adaptive noise cancellers for remote health monitoring systems, Measurement, 2013, 46, p. 3815–3835.
10. Rahman M.Z.U., AhamedShaik R., Reddy D.V.R.K., Efficient and Simplified Adaptive Noise Cancellers for ECG Sensor Based Remote Health Monitoring, IEEE Sensors Journal, 2012, 12(3), p. 566-573.
11. Walach E., Widrow B., The Least Mean Fourth (LMF) Adaptive Algorithm and Its Family, IEEE Transactions on Information Theory, 1984, 30(2), p. 275-283.
12. Nascimento V. H., Bermudez J. C. M., Probability of Divergence for the Least-Mean Fourth Algorithm, IEEE Transactions on Signal Processing, 2006, 54(4), p. 1376-1385.
13. Zerguine A., Convergence and steady-state analysis of the normalized least mean fourth algorithm, Digital Signal Processing, 2007, 17 (1), p. 17-31.
14. Eweda E., Zerguine A., A Normalized Least Mean Fourth Algorithm with Improved Stability, IEEE Asilomar conference 2010.
15. Eweda E., Global Stabilization of the Least Mean Fourth Algorithm, IEEE Transactions on Signal Processing, 2012, 60(3), p. 1473-1477.
16. Eweda E., Bershad N. J., Stochastic Analysis of a Stable Normalized Least Mean Fourth Algorithm for Adaptive Noise Canceling With a White Gaussian Reference, IEEE Transactions on Signal Processing, 2012, 60(12), p. 6235-6244.
17. Thakor N. V., Zhu Y. S., Applications of Adaptive Filtering to ECG Analysis: Noise cancellation and arrhythmia Detection, IEEE Transactions on Biomedical Engineering, 1991, 38(8), p. 785-794.