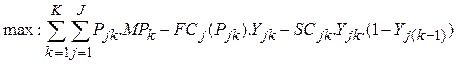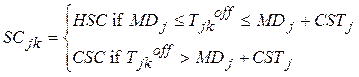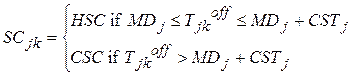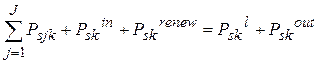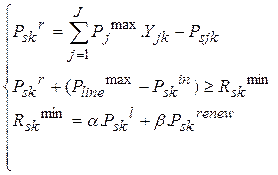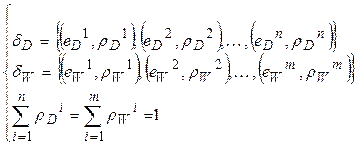Engineering, Environment

 

Generation scheduling of renewable energy resources under uncertainties in competitive environments

 

Emad NEMATBAKHSH, Rahmat-Allah HOOSHMAND*, Moein PARASTEGARI

 

Department of Electrical Engineering, University of Isfahan, Isfahan, Iran

E-mail(s): nematbakhsh.emad@eng.ui.ac.ir, hooshmand_r@eng.ui.ac.ir,

Parastegari@eng.ui.ac.ir

^* Corresponding author, phone: +98 31 37934073, fax: +98 31 37933071

 

Received: January 30, 2017 / Accepted: June 14, 2017 / Published: June 30, 2017

 

Abstract

Over the past few years, utilization of renewable energy resources (RERs) has become an active and interesting area of research in energy management of power systems. In this paper, a new three-stage generation scheduling method is proposed for thermal units and renewable energy resources. In the method, all generation units are bidding in a competitive market along with the external energy tie-line at the point of common coupling. The scheduling problem is solved while considering uncertainties in both generation and demand. At the first stage, Generation Companies (GenCos) use forecasted information (such as market price and climate conditions) to determine their optimal bidding strategy for maximum revenue. In the next stages, independent system operator (ISO) manages available contracts to minimize the operating cost of the power system. The proposed method is applied to a 10-unit network using GAMS software. Simulation results show that the effectiveness of this method is to the benefit of generation companies and ISO in the presence of traditional tie-line.

Keywords

Power Market; Renewable resources; Generation scheduling; Uncertainty

 

Nomenclature

a_j ,b_j ,C_j:           Fuel cost coefficient of unit j

P_sjk:                  Power generation of unit j at time k in scenario 5

P_j^Max , P_j^Min:        Maximum and Minimum generation limit of unit j

MU_j‘ MD_j:       Minimum up and down time of unitj

RU_j ‘ RD_j:        Ramp up and down limit of unit j

FC_j(P_sjk):         Generation cost of unit j at time k in scenario 5

SC_jk:                Startup cost of unit j at time k

HSC_j , CSC_j:   Hot and Cold start-up cost of unit j

T_jk^cold:               Continuous off time of unit j at time k

T^on , T^off:           Continuous on and off time of unit j

P_skⁱⁿ,P_sk^out:      Power imported or exported with tie line at time k in scenario 5

C_sjk^pen:            Penalty for each MWh of unit j at time k in scenario 5

P_jk^best:               Generation bid of unit j at time k

P_sk^r:                  Available reserve at time k in scenario 5

RP_k i MP_k:        Reserve and Market price at time k

RC_sk:              Spinning reserve cost at time k in scenario 5

P_sk^renew:            Generation of renewable units at time k in scenario 5

P_sk^l:                  Demand at time k in scenario 5

R_sk^Min:               Minimum required reserve

P_line^Max:           Line flow limit

α, β:                Reserve factors

 

Introduction

 

Nowadays, renewable energy resources are increasingly used in restructured power systems. One of the main disadvantages of these resources is their uncertain generation. Scheduling problem of generation units without considering renewable resources is a complex problem, yet by considering these resources, scheduling problem becomes more complex. In most studies, the generation scheduling problem is examined from the ISO’s point of view. Hence, the ISO manages the generation units to minimize the total operating cost. In reality, generation scheduling problem is considered from the favorable view of both ISO and GenCos. In this condition, generation scheduling problem could be solved by two general objective functions: cost minimization [5,7,22] or profit maximization [24,25,28] and by Cost Based Unit Commitment (CBUC) or Profit Based Unit Commitment (PBUC) solutions.

In [12-14], scheduling is performed in a cooperative environment. In this case, the hourly load should be lower than the total generation capacity and the system should work in a normal mode [18]. In a normal mode, no power is transferred from or to the system. In [18], two more modes are additionally considered excess demand and excess renewable generation. In these modes, unbalances between generation and consumption are controlled by exchanging power through the tie-line. In [15], a hybrid method is developed through adaptive search which is inspired from artificial immune system and genetic algorithm to carry out profit maximization of generation companies. In a power market, GenCos sell their energy and their reserve to energy and ancillary markets [24]. Changes in energy and reserve prices along with payment methods have a direct effect on the amount of power and reserve bids. There are several methods such as payment for the power delivered and payment for the reserve allocated for reserve market clearing [24]. In a competitive environment, it is not necessary for the power plants to supply the hourly demand. Accordingly, in [24, 29], it is considered that the generated power has to be equal or lower than the hourly demand, so that there is no excess generation in the system. Moreover, [23] tries to determine the optimal or near optimal scheduling to find Influence of improvement of generation scheduling on wheeling cost.

The generation scheduling problem has been studied from different aspects such as considering renewable resources [14-17,21-22,24,26], energy storage systems [14-16,22,25], generation uncertainty [14-18,21,27], reliability indices [27], Emission [1-4,14-15], and demand response [14,28]. In [13-15, 18], it is shown that the penetration of renewable energy resources brings about a decrease in the operating cost. Also, simultaneous scheduling of storage systems and renewable resources improve the performance of renewable energy resources [13]. In [26], the uncertainties of renewable energy resources are considered in retail markets. In this case, the scheduling problem is defined as a Multi-Area Dynamic Economic Dispatch (MA-DED) problem.

Scheduling problems can be solved by different methods. These methods can be divided into two categories: mathematical and meta-heuristic. Mathematical methods which can be used to solve different optimization problems are Lagrangian Relaxation (LR) [24], Evolutionary Programming (EP) [10], and Dynamic Programming (DP) [8]. The Meta-heuristic methods which can be used to solve optimization problems are: Bee Colony [14]; Genetic Algorithm (GA) [8]; Unit Characteristic Classification by using Genetic Algorithm (UCC-GA) [9]; Hybrid Particle Swarm Optimization (HPSO) [12]; and some hybrid methods such as LRGA [11].

In this paper, a hybrid method is presented for the generation scheduling of thermal and renewable units. In this method, a multi-objective problem tries to minimize the generation cost and maximize the profit of GenCos simultaneously. For this purpose, at first the optimal bidding strategy of generation units is determined without considering the power system constraints. Then, based on historical data, all scenarios of renewable energy resources and system loads are generated. Finally, by considering all scenarios, the main scheduling problem is modeled by meeting the security constraints of the system and generation units. Simulation results indicate that the proposed method can decreases the cost and increases the profit of the coordinated thermal and renewable units by using the traditional tie-line.

 

Material and method

Problem Formulation

Generation units can be categorized into two main categories: Dispatch able units and Non-Dispatch able units. In schedulable units, the scheduling program is determined based on fuel cost and other ancillary costs. The goal of the operator of these units is to maximize the profit. Operators of these units submit their bids to the market and if their bids are accepted, the ISO should use the bids in the scheduling program. If there are any violations between scheduling program and the actual state of the units, the ISO should pay the imbalance cost to GenCos. On the other hand, there are uncertainties in the power generation of the non-dispatch able units such as wind units; so, it is necessary to model these uncertainties to reach the optimal scheduling program. First, the generation of non-schedulable units is forecasted and then the uncertainties are modeled through the historical data by scenario method to model these uncertainties. It should be noted that the ISO schedules units according to their contracts, the scenarios of the generation of renewable resources, and the load scenarios. ISO uses renewable resources first, then uses the schedulable units, and finally uses tie-line power in its scheduling program.

 

 

Optimal bidding strategy of GenCos

In this section, optimal bidding strategy of generation units is determined. To determine the optimal bidding strategy of the units, it is first necessary to determine the pattern of the daily prices on the basis of the historical prices data and price fluctuations. Then, optimal bidding strategy of the units is determined by solving optimization problem consisting of an objective function and a set of constraints. The objective function of this problem is as follows:

(1)

The objective function consists of three parts. The first part represents the sales profit in the market. The second part represents the cost of generated power and the last part represents the startup cost. Y_jk variable is a binary variable indicating the status of unit j in period k. Generation and startup costs can be determined as follows:

	(2)
	(3)

In order to determine the optimal bidding strategy of the units, it is necessary that to consider the constraints of the generation units. These constraints are as follows:

1.     Generation limits: The output power must be within allowable limits:

(4)

2.     Minimum up and down times:

	(5)
	(6)

3.     Ramp up and ramp down limits: The change in the output power of the units must comply with the following limits:

	(7)
	(8)

 

 

Scheduling problem from the point of view of ISO

The scheduling problem used by ISO is introduced in this section. ISO executes the scheduling problem and the inputs of the problem are the generation bids (determined in the last subsection), the scenarios of the generation of the renewable energy resources, and the load scenarios. The objective of this scheduling problem is to minimize the operation cost of the system. This objective function is as follows.

(9)

This objective function (Eq. (9)) consists of four parts. In (9),  represents the violation penalty for any bid for unit j at period k in scenario s.  represents the cost of the spinning reserve at period k in scenario s. Also,  presents the energy cost of the tie-line. Meanwhile,  parameter indicates the probability of scenario s. Also, imbalanced and the reserve cost can be calculated as follows:

	(10)
	(11)
	(12)
	(13)

Constraints of the scheduling problem from the point of view of ISO are as follows:

1.     Generation Limits: This constraint is the same as that in (4);

2.     Minimum up and down times: These constraints are the same as those presented in (5) and (6);

3.     Ramp up and ramp down limits: These constraints are the same as those presented in (7) and (8);

4.     System power balance: the following equation represents the load balance equality.

(14)

Where: P_skⁱⁿ and P_sk^out represent the input and output transmitted power by the tie-line at period kin scenario s, respectively. Also, P_sk^renew represents the power generated by the renewable resources at period k in scenario s, and P_sk^l represents the demand at period k in scenario s.

1.  System reserve: the reserve of the network must be provided under the following conditions.

(15)

In Eq. (15), the spinning and non- spinning reserve value is specified. The total available reserve must be at least equal to required amount (i.e. Percentage of hourly demand or biggest generation unit capacity). P_sk^r represents the value of the spinning reserve provided by schedulable units at period k in scenario s. P_line^max - P_skⁱⁿ represents the non-spinning reserve value provided by the tie-line at period k in scenario s. Also, R_sk^min represents the minimum reserve requirements at period k in scenario s. The coefficients α and β represent the percentage of the demand and the generation of the renewable resources for the minimum reserve requirements.

2.  Tie-line flow limits: The value of the limits are as follows:

	(16)
	(17)

 

A method proposed for the defined problem

The algorithm of the proposed method is shown in Figure 1.

 

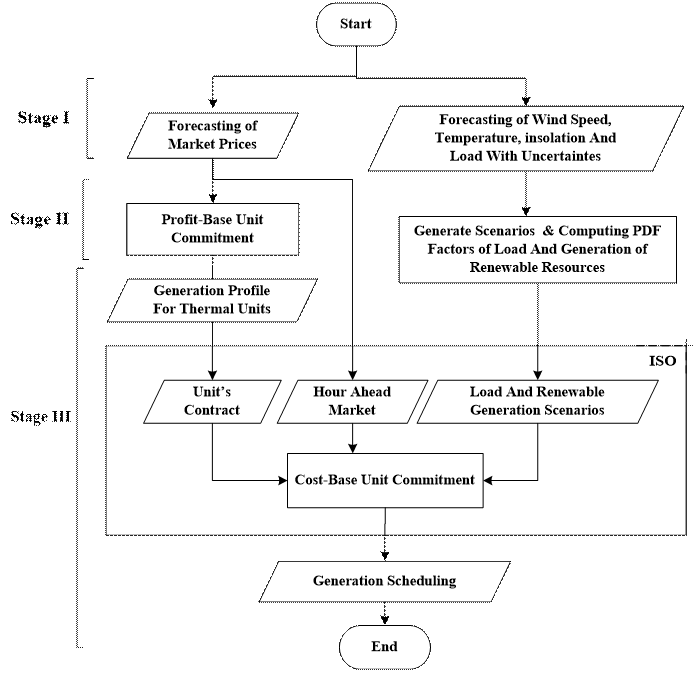
Figure 1. The proposed algorithm

 

As shown in this figure, this algorithm consists of three stages. In the first stage, the input data includes the market price forecasts, the predicted demand, and the forecast determined for the generation of renewable resources. In the second stage, by solving the PBUC problem, the optimal bidding strategies of GenCos are determined. The scenarios of the renewable generation and demand should be determined at this stage as well. In the last stage, based on previous results, the scheduling problem is modeled and solved by considering the power system constraints from the point of view of ISO.

Generation scheduling problems can be examined with regard to two contexts: Cooperative and Competitive. In the cooperative context, the generation units have to meet the demand with minimum reserve requirements. In this case, the network has no dealings with the outside network and the network must be self-sufficient to meet its demands. In the competitive context, the system operator can use the tie-line power to satisfy the demand. In this case, the system generation can be lower or higher than that of the demand required. Obviously, the profit of GenCos in competitive markets is more than that of cooperative markets. It should be noted that in a competitive context, the GenCos offer bids in a way that they make the maximum profit. But in a cooperative context, the GenCos should satisfy the demand. In the following, the three stages of the proposed method are introduced.

 

First stage

At this stage, the information required for solving the scheduling problem is determined as an input data to the generation scheduling problem.

These input data are as follows:

1.      Forecasted day-ahead market prices.

2.      Forecasted load and its scenarios.

3.      Forecasted generation of renewable resources for the next 24 hours and its scenarios

 

Second stage

In this stage, by using the information determined in the previous stage, optimal bidding strategies of the schedulable units are determined. For this purpose, the following data should be determined.

1.      Bids of the schedulable GenCos: the schedulable GenCos determine their optimal bidding strategy based on market prices by solving the problem presented in section (2-1).

2.       Demand scenarios: ISO calculates the demand scenarios based on historical information. The method used for scenario generation is described in the next sub-section.

Scenarios for the renewable generation of energy resources: based on the historical data of the renewable energy resources, renewable generation scenarios can be determined. The method used for the scenario generation is described as follows.

Scenario generation method: One of the main methods to generate the load and renewable power scenarios is to discretize the ‎probability distribution function (PDF) of the forecasting error [18]. ‎Demand and wind power generation errors can be modeled by using this method based on normal PDFs. Each continuous PDF is discretized to create a set of finite states such that a probability is assigned to each state according to its PDF. Forecasting errors are defined as per-unit and can be changed several times in one scenario. We assumed that these values are provided by renewable resources. The discrete sets of the load  and wind power  forecasting errors are described as follows:

	(18)
	(19)

Where:  - the error of scenario n of the forecasted load,  - the corresponding probability, and n - the total number of load scenarios. Also, , and  - the error and the probability of the wind generation forecast of the m-th scenario and m - the total number of wind generation scenarios. S represents the total number of scenarios.

In this stage, the data which is determined in the previous stages are used to schedule units. The optimal bidding strategy of the schedulable units determined in the previous stage will be considered as contracts on the market. Also, all the pieces of information such as the market price and the scenarios are collected for primary generation scheduling by solving the objective function (9).

 

Results and discussion

 

In order to illustrate the advantages of the algorithm presented in Section 3, this algorithm has been implemented on a 10-Units power system. At first, simulation results for both the cooperative and competitive contexts are introduced and then the results are compared with those of other studies. Finally, the results of the proposed algorithms are evaluated. It should be noted that DICOPT (Discrete and continuous optimizer) solver of GAMS software is used for solving the optimization problem. This solver is a program for solving mixed-integer nonlinear programming (MINLP) problems that involve linear binary or integer variables and linear and nonlinear continuous variables. While the modeling and solution of MINLP optimization problems have not yet reached the stage of maturity and reliability achieved by linear, integer, or non-linear programming modeling, these problems still have rich areas of application. The MINLP algorithm inside DICOPT solves a series of NLP and MIP sub-problems. NLP and MIP solvers that used for this simulation are CONOPT and CPLEX.

 

Initial data

The case under study consists of 10 thermal units with a total capacity of 1662 MW. The details of the 10 power units are presented in appendix A. The demand profile and the hourly market price are shown in Table 1 [24]. In this system, the required reserve is 10% of the hourly demand (α=0.1).

 

Table 1. Forecasted demands and spot market price

 

Comparing GAMS results with those of other solvers

By comparing the simulation result with [8-12, 24], scheduling problem is solved by both CBUC and PBUC objective functions [24]. CBUC problem is considered in the cooperative context and PBUC problem in the competitive context.

 

              CBUC Problem

The purpose of this scheduling is to minimize the operational cost resulting from limitations in the generation and the network. The results of the GAMS software compared with those of other methods are shown in Table 2.

 

 

Table 2. Comparing simulation results of proposed method with others

 

The responses obtained with respect to occurrence are divided into three categories: the best, average and the worst. Also, because of the unavailability of all responses, the term N/A is used in some methods. It is clear that the GA [8], DP [8], and LR [24] methods have the same answer and UCC-GA [9] and LRGA [11] attain better results. The results obtained by the GAMS software shows $563937.7 that is less than the amount obtained by the best solution in [12]. Numerical generation result of the 10 thermal units for the day-ahead scheduling is shown in Table 3. Compared to [24], better results are obtained due to changes in the generation power of units 5 and 6 over a period of 23.

Table 3. Power setting and generation cost of 10-Units

              PBUC Problem

The purpose of this scheduling is to maximize the profit of generation companies due to constraints and market price fluctuations. In a competitive context, reserve payment can be made in different ways: payment for an allocated reserve and payment for a reserve that is actually used. The second method is the method used in this section. The price of the ancillary service market is fixed at five times the spot price. In Table 4, the results of the generation and reserve scheduling for 10 units are shown. The results show that under these conditions the maximum profit is $112642.1. This value can be calculated by subtracting the total cost from the revenue in Table 4 which is $4767.1 more than [24]. This difference is due to changes in the generation rates and reserve power in stations 2, 5, and 6.

Table 4. Power setting and generation cost of 10-Units

 

To demonstrate the capabilities of the proposed algorithm in the network, the influence of market price fluctuations, penetration of renewable resources, and uncertainty in the scheduling problem have been tested. Four intended cases are shown in Table 5.

Case 1: Scheduling is offered without renewable resources, uncertainty, and volatility of the market price.

Case 2: Scheduling is offered with the effects of fluctuations in the market price.

Table 5. Cases considerations

 

Case 3: Scheduling is offered with renewable resources and fluctuations in the market price.

Case 4: Scheduling is offered with renewable resources, uncertainty, and volatility of the market price.

In the scheduling, communication line capacity is set to 700 MW and the coefficient α= 0.1. Penalties for each megawatt hour are equal to the spot market. The reserve price is equal to 25% of the market price. In this case, no penalties have been paid to the generation companies. So, the generation companies are working at their optimum point for maximum benefit. The results show that the cost is reduced from 565825 to 543034.9 because of the exchanged power through the lie-line. Also, by the use of the proposed method the profit is increased about $2531.9 in comparison with the generation pattern of thermal units in [8, 24].

 

Discussion of case 1:

The results of the proposed algorithm, in case 1, are presented in Table 6.

Table 6. Simulation result of proposed method – Case 1

 

Using renewable energy resources and storage systems presented in [15] leads to, operating cost about $554385.64. This cost is more than the cost of the proposed method. So, by selling the surplus power to the market, ISO not only did not pay any penalties to GENCOs but also reduced the operational cost. The details of the proposed scheduling are shown in Table 7.

Table 7. Power setting and reserve cost of 10-Units – Case 1

 

According to this table, it is clear that due to the cheaper cost of the market price compared to the marginal cost of thermal units at peak points, lack of power is supplied by the tie-line. By canceling the contracts of the expensive units over these hours, the system operator purchases the required power from the market and vice versa.

 

Discussion of case 2:

In the case, the hourly price pattern is taken from [25]. To maximize profits, the generation pattern of thermal units is shown in Figure 2. According to this figure, units 7 to 10 did not offer any power because of the average market price is low.

 

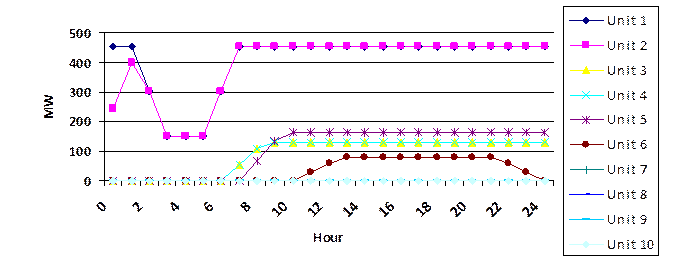
Figure 2. Profit-Base unit commitment of 10-Units – Case2

 

As we can see in Table 8, no penalties have been paid to the units. So, the plants are working at their optimum point for maximum profit.

Table 8. Simulation result of proposed method – Case 2

 

As it is shown in the table, the total cost of the system is reduced from $543034.9 to $529663.9, because a part of the energy is provided from power market via the tie-line. On the other hand, price uncertainty leads to an increase in the total profit of the system from $110406.9 to $147079.4. The hourly rates of the purchased () and sold () power are shown in Table 9.

Table 9. T-Line power setting – Case 2

 

Discussion of case 3:

In this case, besides considering the volatility of the market price, there is a wind farm with a capacity of 150 MW in addition to thermal power units [14] with a coefficient of β = 0.13 [18]. In this new condition, operational cost is decreased from $529663.9 to $445948.4 compared to case 2. Also, the operating cost is $84412.4 which is less than ‎ [14]. So, with same amount of wind power, the use of the proposed method leads to more profit by selling the exceeded power. In both cases of 2 & 3, profit is equal to $147079.4. The details of the scheduling in case 3 are shown in Table 10.

Table 10. T-Line & renewable resources power setting – Case 3

 

According to this table, it is clear that at any period the amount of the sale or purchase increased or decreased based on generation amount of renewable resources, respectively. Of course, it also depends on the capacity of the tie-line.

 

Discussion of case 4:

Results of case 4 are presented in Table 11. This table shows the effects of using proposed multi-scenario stochastic model to solve the day-ahead UC problem.

 

Table 11. Discrete probability distribution of wind and load

 

As shown in this table, five scenarios are considered for demand errors and wind power generation [15]. So, there are 25 scenarios employed to calculate through the use of Eq. (10). The scenario details include the PDFs and per unit errors as shown in Figure 3.

 

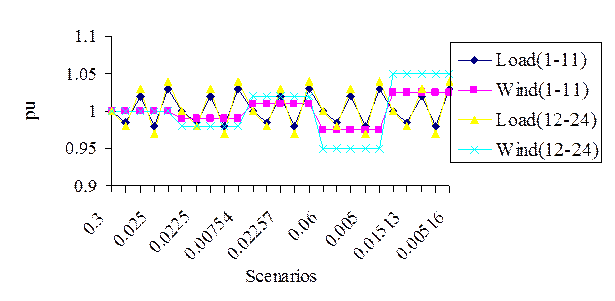
Figure 3. Scenario details

 

The operational cost of the system is increased from $445948.4 to $447112.4 and the profit is equal to case 3. By checking the expected values, it is clear that the most frequent scenario is no. 20. In this scenario, due to the decreased generation of renewable energy and increased demand, costs have increased significantly. Scenario 3 is the most expected one. It occurs when the demand is not changed and the renewable energy generation is reduced.

 

Conclusions

 

In this paper, a new method is presented for the generation scheduling in a competitive environment. Simulation results show that power trade via tie-line makes the generation scheduling problem more flexible. Therefore, ISO can prevent major penalties by exchanging power in the presence of high uncertainty. On the other hand, the proposed algorithm increases the profit of GenCos by following their bidding strategies as much as possible. As a result, the proposed algorithm improves the performance of energy management system by increasing the profit of both participants in the market.

 

Appendix

Characteristic information for economic dispatch and unit commitment problems of units for the 10-unit system are given in Tables 1 and 2, respectively.

 

Table a.1. Main characteristics of thermal units

 

Table a.2. Additional characteristics of thermal units

 

 

 

 

 

References

 

1.    Ahmadi, A., Sharafi Masouleh, M., Janghorbani, M., Yadollahi Ghasemi Manjili, Navid, Sharaf, A. M., Esmaeel Nezhad, A., Short term multi-objective hydrothermal scheduling, Electric Power Systems Research, vol. 121, pp. 357–367, 2015.

2.    Vithayasrichareon, P., MacGill, I. F., Incorporating short-term operational plant constraints into assessments of future electricity generation portfolios, Applied Energy, vol. 128, pp. 144–155, 2014.

3.    Hooshmand, R.-A., Parastegari, M., Morshed, M. J., Emission, reserve and economic load dispatch problem with non-smooth and non-convex cost functions using the hybrid bacterial foraging-Nelder–Mead algorithm, Applied Energy, vol. 89, no. 1, pp. 443–453, 2012.

4.    Glotić, A., Zamuda, A., Short-term combined economic and emission hydrothermal optimization by surrogate differential evolution, Applied Energy, vol. 141, pp. 42–56, 2015.

5.    Rasoulzadeh-akhijahani, A. Mohammadi-Ivatloo, B., Short-term hydrothermal generation scheduling by a modified dynamic neighborhood learning based particle swarm optimization, International Journal of Electrical Power & Energy Systems, vol. 67, pp. 350–367, 2015.

6.    Uyar, A. Ş., Türkay, B., Keleş, A., A novel differential evolution application to short-term electrical power generation scheduling, International Journal of Electrical Power & Energy Systems, vol. 33, no. 6, pp. 1236–1242, 2011.

7.    Zhang, J., Lin, S., Qiu, W., A modified chaotic differential evolution algorithm for short-term optimal hydrothermal scheduling, International Journal of Electrical Power & Energy Systems, vol. 65, pp. 159–168, 2015.

8.    Kazarlis, S. A., Bakirtzis, A. G., Petridis, V., A genetic algorithm solution to the unit commitment problem, IEEE Trans. Power Syst., vol. 11, no. 1, pp. 83–92, 1996.

9.    Senjyu, T., Yamashiro, H., Uezato, K., Funabashi, T., A unit commitment problem by using genetic algorithm based on unit characteristic classification, In Winter Meeting of the Power Engineering Society, 58–63, 2002.

10. Juste, K. A., Kita, H., Tanaka, E., Hasegawa, J., An evolutionary programming solution to the unit commitment problem,” IEEE Trans. Power Syst., vol. 14, no. 4, pp. 1452–1459, 1999.

11. Chuan-Ping Cheng, Chih-Wen Liu, Chun-Chang Liu, Unit commitment by Lagrangian relaxation and genetic algorithms, IEEE Trans. Power Syst., vol. 15, no. 2, pp. 707–714, 2000.

12. Ting, T. O., Rao, M., Loo, C. K., A Novel Approach for Unit Commitment Problem via an Effective Hybrid Particle Swarm Optimization, IEEE Trans. Power Syst., vol. 21, no. 1, pp. 411–418, 2006.

13. Logenthiran, T., Srinivasan, D., Short term generation scheduling of a Microgrid, In TENCON 2009 - 2009 IEEE Region 10 Conference, 1–6.

14. Govardhan, M. and Roy, R., Generation scheduling in smart grid environment using global best artificial bee colony algorithm, International Journal of Electrical Power & Energy Systems, vol. 64, pp. 260–274, 2015.

15. M. Kamel, Ahmed M. Azmy, A. Abou ElEla, Ahmed I.A. Shobair, Optimal Management and Operation of a Hybrid Energy System Based on Wind Energy Units, Journal of Electrical Systems, vol. 9, no. 2, pp. 191–202, 2013.

16. Cau, G., Cocco, D., Petrollese, M., Knudsen Kær, S., and Milan, C., Energy management strategy based on short-term generation scheduling for a renewable microgrid using a hydrogen storage system, Energy Conversion and Management, vol. 87, pp. 820–831, 2014.

17. Osório, G. J., Lujano-Rojas, J. M., Matias, J., and Catalão, J., A fast method for the unit scheduling problem with significant renewable power generation, Energy Conversion and Management, vol. 94, pp. 178–189, 2015.

18. ZeinAlabedin, A. M., El-Saadany, E. F., Salama, M. M. A., Generation scheduling in Microgrids under uncertainties in power generation, in 2012 IEEE Electrical Power & Energy Conference (EPEC), 133–38.

19. Hinojosa, V. H. and Leyton, C., Short-term hydrothermal generation scheduling solved with a mixed-binary evolutionary particle swarm optimizer, Electric Power Systems Research, vol. 92, pp. 162–170, 2012.

20. Gjorgiev, B., Kančev, D., Čepin, M., A new model for optimal generation scheduling of power system considering generation units availability, International Journal of Electrical Power & Energy Systems, vol. 47, pp. 129–139, 2013.

21. Simoglou, C. K., Kardakos, E. G., Bakirtzis, E. A., Chatzigiannis, D. I., Vagropoulos, S. I., Ntomaris, A. V., Biskas, P. N. et al., An advanced model for the efficient and reliable short-term operation of insular electricity networks with high renewable energy sources penetration, Renewable and Sustainable Energy Reviews, vol. 38, pp. 415–427, 2014.

22. Wang, Y., Zhang, K., Teng, X., Ding, Q., Huang, X., Coordinated operation of wind power and other resources considering power system requirements, J. Renewable Sustainable Energy, vol. 7, no. 2, pp. 23121, 2015.

23. I. Kranthi Kiran, A. Jaya Laxmi, Influence of improvement of generation dispatch together with generation scheduling on wheeling cost, Journal of Electrical Systems, vol. 10, no. 1, pp. 93–116, 2014.

24. Logenthiran, T., Woo, W. L., Van Phan, T., Lagrangian relaxation hybrid with evolutionary algorithm for short-term generation scheduling, International Journal of Electrical Power & Energy Systems, vol. 64, pp. 356–364, 2015.

25. Parastegari, M., Hooshmand, R.-A., Khodabakhshian, A., Zare, A.-H., Joint operation of wind farm, photovoltaic, pump-storage and energy storage devices in energy and reserve markets, International Journal of Electrical Power & Energy Systems, vol. 64, pp. 275–284, 2015.

26. Soroudi, A. and Rabiee, A., Optimal multi-area generation schedule considering renewable resources mix: a real-time approach,” IET Generation, Transmission & Distribution, vol. 7, no. 9, pp. 1011–1026, 2013.

27. MacCormack, J., Hollis, A., Zareipour, H., Rosehart, W., The large-scale integration of wind generation: Impacts on price, reliability and dispatchable conventional suppliers, Energy Policy, vol. 38, no. 7, pp. 3837–3846, 2010.

28. Saebi, J. and Hossein Javidi, M., Economic evaluation of demand response in power systems with high wind power penetration, J. Renewable Sustainable Energy, vol. 6, no. 3, pp. 33141, 2014.

29. Sharma, D., Trivedi, A., Srinivasan, D., Thillainathan, L., Multi-agent modeling for solving profit based unit commitment problem, Applied Soft Computing, vol. 13, no. 8, pp. 3751–3761, 2013.

30.       Amjady, N. and Vahidinasab, V., Security-constrained self-scheduling of generation companies in day-ahead electricity markets considering financial risk, Energy Conversion and Management, vol. 65, pp. 164–172, 2013.