Engineering, Environment
A new design for a robust fractional Smith predictor controller based fractional model
Riadh DJABRI1*, Moussa SEDRAOUI2, Abdelaziz YOUNSI3
1,3Department of electronic and telecommunication. University of 8 May 1945 Guelma, Algeria
2 Laboratoire des télécommunications, Université 8 Mai 1945 Guelma, Algeria
E-mail(s): 1 riadh.djabri@yahoo.com; 2 msedraoui@gmail.com; 3 az_younsi@yahoo.fr
* Corresponding author, phone: +213 670 199 780
Received: December 06, 2016 / Accepted: June 14, 2017 / Published: June 30, 2017
Abstract
The present paper deals with the fractional controller synthesis method based on the Smith Predictor (SP) scheme using the fractional model, where the obtained feedback control system satisfies both time and frequency domains specifications. Both fractional controller and model parameters are designed through solving two proposed constraint optimization problems and using the same meta-heuristic algorithm, called Particle Swarm Optimization (PSO). The proposed method is used to control some actual systems where the dynamic behaviour of each one is modelled by the mismatch model with dead time. The obtained simulation results are compared in time and frequency domains with those given by the conventional integer and fractional SP controllers to validate the effectiveness of the proposed method.
Keywords
Fractional calculus; Dead time; Smith Predictor; Fractional model; Fractional PID controllers; Optimization; PSO Algorithm; Identification
Introduction
Systems that possess a dead time are hard to be controlled by the classic controllers such as the proportional integral derivative (PID) controller [1]. However, they could be controlled using the Smith Predictor (SP) scheme, which is commonly used for this type of systems [2, 3]. This strategy control has been widely studied in recent research papers with different propositions leading to one goal [4]: an optimal controller based upon an optimal model obtained in two steps, which are (1) the modelling step and (2) the controller synthesis step [5]. In order to ensure a low tracking error index, a low-cost control, and a less sensitivity to both sensor noises and load disturbance signals [6, 7].
It is well known that the development of tuning rules, for the process with dead time, requires a perfect model that provides an ideal mathematical model with adequate details [8]. This model should provide a precise description of the real dynamic of the process to be controlled. Unfortunately, a perfect mathematical model is rarely available in practice due to the strong nonlinear dynamic of the process [9, 10]. To provide an exact description of the system, the process should be reduced in a suitable template such as a First-Order Plus Time Delay (FOPTD) model [8, 11] or a Second-Order Plus Time Delay (SOPTD) model [8, 12]. Various tuning rule methods based upon these models have been developed to approximate the dynamic of the process and guarantee the good robustness margin of the feedback control system [8, 13]. Among them, Zhuang and Atherton [14] proposed a tuning rule method for integer order PID controllers to handle FOPTD model, which is rather a poor approximation for higher-order processes [15]. Palmor [16] developed an auto-tuning algorithm for the Smith dead time compensator using a FOPTD model for stable plants. This algorithm estimates two points on the process of the Nyquist curve via automatic generation of the controlled limit cycles. The obtained points are then used in a least square procedure to estimate the model parameters, in which a primary integer order controller has been designed through the empirical Zeigler-Nichols method. Hang [17] proposed a method for auto-tuning and self-timing the modified SP using the relay feedback strategy. On the other hand, Wang [11] proposed an analytical way to design series of FOPTD models, in which the obtained controller is designed by only one of them. Kaya [18] suggested three types of integer order models, which are: a stable SOPTD, an integrating FOPTD, and an unstable FOPTD. Unfortunately, the previous integer models can generate errors in the estimation step of the model parameters, due to a large dead time delay and a higher order process. Baiyu [19] used the Radial Basis Function Neural Network (RBFNN) method to find FOPTD parameters for a nonlinear process [20, 21]. However, this method did not produce an analytical expression for the model. As a result, the controller parameters are not easy to design using the previous strategies [22, 23]. Notice that, the fractional order carried on the Laplace operator can be approximated into the usual integer transfer function that contains the infinite poles and zeros. Therefore, many advanced control strategies benefit to the previous property, in which the obtained robust fractional controller may be synthesized with less unknown parameters [24]. The obtained controller should satisfy several imposed specifications when the model parameters change in a wide range. Consequently, the size of the optimization problem becomes considerably reduced ensuring the success of the optimization tool.
The aim of this work is to enhance the performances of the closed loop SP scheme for systems with dead time. To achieve this goal, a new fractional-order model has been proposed. Also, a synthesis method based on SP scheme and an optimization problem with reduced constraints to design the proposed robust SP fractional controller. This proposed strategy ensures a good rejection dynamic, a good set-point tracking dynamic, and a good attenuation dynamic of the sensor noises for two different plants.
Material and method
In this section, we will present methods which are used in the modelling and the controller synthesis steps to obtain the proposed controller. But for the sake of clarity, let us define the basic notations of the fractional calculus and of the SP method [25].
Smith Predictor
The scheme proposed by Smith for the dead time compensation is shown in figure 1.
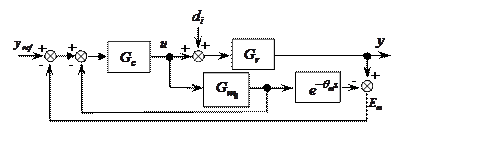
Figure 1. Smith Predictor scheme
Where:![]() ,
, ![]() ,
, ![]() and
and ![]() denote,
respectively, the process output, the control signal, the set-point reference,
and the plant input disturbance. Moreover, Gr is the actual process,
denote,
respectively, the process output, the control signal, the set-point reference,
and the plant input disturbance. Moreover, Gr is the actual process,
![]() is the proposed fractional model, which
will be determined later by an adequate optimization tool. Gc is the
proposed fractional controller, which will be designed through the previous
fractional model. Finally, Gm0 is the free dead time part of the
proposed model Gm.
is the proposed fractional model, which
will be determined later by an adequate optimization tool. Gc is the
proposed fractional controller, which will be designed through the previous
fractional model. Finally, Gm0 is the free dead time part of the
proposed model Gm.
In this paper, the SP synthesis controller has two phases (i) the modelling step, and (ii) the controller synthesis step. In the modelling step, the main goal is to find an efficient fractional model that perfectly fits the frequency response of the actual process. In addition, the main goal of the controller synthesis step is to design a robust fractional controller that satisfies several specifications.
Fractional calculus
The fractional calculus is the subject of interest for more than
three centuries. The number of applications where the fractional calculus has
been used is growing rapidly. The obtained fractional mathematical model can
describe a real object with greater accuracy than conventional integer model.
Fractional calculus is a generalization of the integration and differentiation
to the fractional order fundamental operator![]() ,
where
,
where ![]() and
and ![]() are
the limits and
are
the limits and ![]() is the order of the
operation. Among many definitions, two are commonly used for the generalized
fractional integral-derivative operations, which are the Grunwald-Letnikov (GL)
and the Riemann-Liouville (RL) definitions.
is the order of the
operation. Among many definitions, two are commonly used for the generalized
fractional integral-derivative operations, which are the Grunwald-Letnikov (GL)
and the Riemann-Liouville (RL) definitions.
The GL definition is given by Eq. (1), [25]:
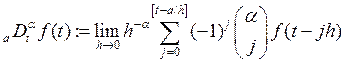 (1)
(1)
Where: ![]() means the integer part.
means the integer part.
The RL definition is given by the following Eq.(2), [25]:
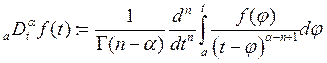 (2)
(2)
Where: ![]() and
and ![]() is
the Euler's
is
the Euler's ![]() function.
function.
For convenience, the Laplace domain is commonly used to describe the
fractional integral-derivative operation. According to the RL definition, the
Laplace transform of equation (2), under zero initial condition and![]() , is given by equation (3):
, is given by equation (3):
![]() (3)
(3)
Notice that, the fractional-order transfer function (FOTF) of powers
of ![]() requires approximating its fractional
parts into usual integer transfer function with a similar behaviour. This goal
is achieved by using the Oustaloup method [24] where
requires approximating its fractional
parts into usual integer transfer function with a similar behaviour. This goal
is achieved by using the Oustaloup method [24] where ![]() can
be approximated in the specified frequency range
can
be approximated in the specified frequency range ![]() with
the choice of the integer number
with
the choice of the integer number![]() , Eq. (4):
, Eq. (4):
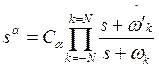 (4)
(4)
According to equation (4), zeros, poles, and gain are respectively given by Eq. (5-7):
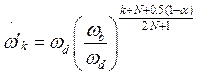 (5)
(5)
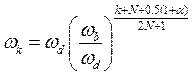 (6)
(6)
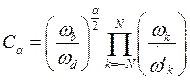 (7)
(7)
The implementation
problem of ![]() (where
(where![]() ) is
solved by considering
) is
solved by considering ![]() where
where![]() is the integer part
of
is the integer part
of ![]() and
and ![]() (where
(where![]() ) is determined by the Oustaloup method
[24] using equations (4) to (7).
) is determined by the Oustaloup method
[24] using equations (4) to (7).
On the proposed fractional model
In the modelling step, the fractional model parameters are determined from solving the proposed optimization problem using the particle swarm optimization (PSO) algorithm. The cost function is formulated as the Least Mean Square Error LMSE criterion, which is given by the discrepancy value, at each logarithmic space frequency, between both magnitudes of the actual process and the proposed fractional model. Furthermore, the inequality constraints are given through the absolute discrepancy value, at each logarithmic space frequency, between both phases of the actual process and the proposed fractional model. Hence, the transfer function of the proposed fractional model is Eq. (8-9):
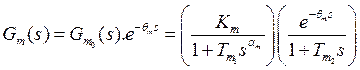 (8)
(8)
![]() (9)
(9)
Where: the model parameters are given by the vector ![]() (see equation (9)), which are:
(see equation (9)), which are: ![]() gain,
gain, ![]() -
time constants of first order transfer function,
-
time constants of first order transfer function, ![]() -
the order of the fractional system, and
-
the order of the fractional system, and ![]() - the
dead time value.
- the
dead time value.
Notice that, the above fractional model (see equation (8)) combines two transfer functions. The first one, given in the right, presents the integer FOPTD model that is commonly used in the modelling step of the standard SP design method. However, the second transfer function, given in the left, presents the stable multi-lag fractional model, which will be used later in the controller synthesis step. Moreover, the proposed fractional model parameters are usually determined by resolving the following optimization problem:
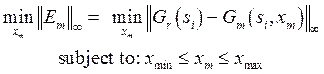 (10)
(10)
According to previous works, several methods have been proposed to reformulate the optimization problem given in equation (10). Among them, the chosen optimization problem is defined as follows Eq. (11):
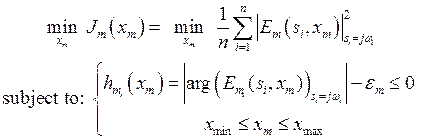 (11)
(11)
Where:![]() denotes the cost function to
be minimized,
denotes the cost function to
be minimized, ![]() is the number of frequencies
chosen from the frequency range
is the number of frequencies
chosen from the frequency range ![]() ,
, ![]() is the positive scalar which presents
the minimum distance allowed between both phases of the actual process and the
proposed fractional model,
is the positive scalar which presents
the minimum distance allowed between both phases of the actual process and the
proposed fractional model, ![]() and
and![]() are, respectively, the lower and upper
bounds that limit the design vector
are, respectively, the lower and upper
bounds that limit the design vector ![]() ,
, ![]() , where
, where ![]() are the
inequality constraints presenting the absolute error between both phases of the
actual process and the proposed model.
are the
inequality constraints presenting the absolute error between both phases of the
actual process and the proposed model.
Knowing that, the optimal solution of the optimization problem given by equation (11) is difficult due to the high number of the inequality constraints. To resolve this difficulty, the optimization problem will be transformed into the bounded constraints optimization using the same idea proposed in [23]. Afterward, the fractional model parameters are easily determined from its optimal solution using the PSO algorithm.
Synthesis Controller Step
In synthesis
controller step, the proposed fractional controller is designed using the
similar way proposed by Wang in [11]. Therefore, the free dead time part of the
proposed model ![]() can be decomposed into two
transfer functions such as, Eq. (12):
can be decomposed into two
transfer functions such as, Eq. (12):
![]()
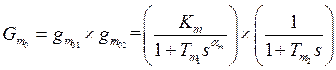 (12)
(12)
Where: ![]() and
and ![]() are,
respectively, the fractional and integer free dead time parts of the proposed
fractional model. Hence, the modified mismatch SP scheme is shown in figure 2
[11]:
are,
respectively, the fractional and integer free dead time parts of the proposed
fractional model. Hence, the modified mismatch SP scheme is shown in figure 2
[11]:
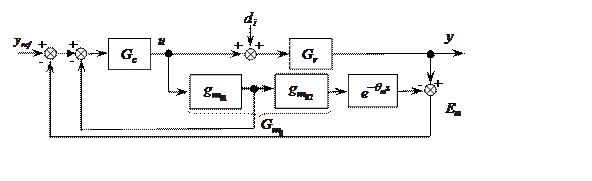
Figure 2. Smith Predictor
It can be simplified as the following modified mismatch SP schemes, which are given by both figures 3 and 4 [11].
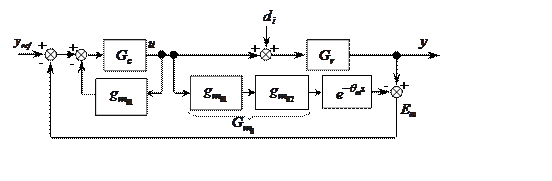
Figure 3. Modified mismatch SP (first version)
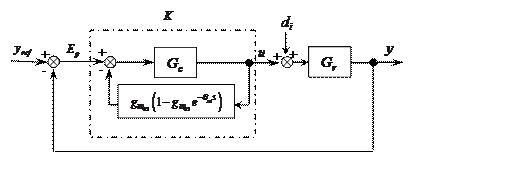
Figure 4. Modified mismatch SP (second version)
Where: Ep denotes the tracking error between the process output and the set-point reference.
Let us consider now ![]() the controller
parameter vector that defines the transfer function of the proposed fractional
controller
the controller
parameter vector that defines the transfer function of the proposed fractional
controller![]() , which is defined by Eq. (13):
, which is defined by Eq. (13):
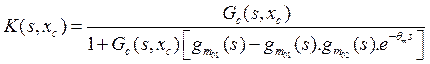 (13)
(13)
According to figure 4, the general scheme of the closed-loop system can be presented.
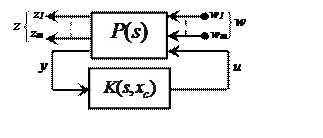
Figure 5. Block diagram of the feedback control system
Where: ![]() is the generalized plant
given by Eq. (14):
is the generalized plant
given by Eq. (14):
![]() (14)
(14)
As depicted in figure 5, the closed-loop system has ![]() exogenous inputs, which are presented
by the vector
exogenous inputs, which are presented
by the vector![]() including various exogenous
inputs such as sensor noises, plant input disturbances
including various exogenous
inputs such as sensor noises, plant input disturbances![]() ,
plant output disturbances
,
plant output disturbances![]() , and set point
references
, and set point
references![]() . In addition, it has also
. In addition, it has also ![]() exogenous outputs that are presented
by the vector
exogenous outputs that are presented
by the vector ![]() where all imposed
characteristics are considered. The proposed fractional controller
where all imposed
characteristics are considered. The proposed fractional controller ![]() utilizes the measured output vector
utilizes the measured output vector ![]() to elaborate the control vector
to elaborate the control vector![]() , which modifies the natural behaviour
of the process
, which modifies the natural behaviour
of the process ![]() (see equation (14)). The
obtained controller should satisfy some imposed specifications such as, a good
tracking dynamic of set point references, a good attenuation of all load
disturbances and sensor noises. These requirements are formulated as the
following optimization problem [5]:
(see equation (14)). The
obtained controller should satisfy some imposed specifications such as, a good
tracking dynamic of set point references, a good attenuation of all load
disturbances and sensor noises. These requirements are formulated as the
following optimization problem [5]:
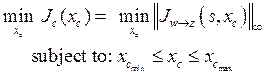 (15)
(15)
Where: ![]() denotes the closed-loop
transfer matrix between both exogenous input
denotes the closed-loop
transfer matrix between both exogenous input ![]() and
output
and
output ![]() vector.
vector.
Proposed Fractional-order Controller
The proposed robust fractional controller is given by the following fractional structure, Eq. (16):
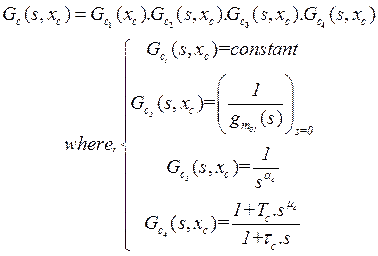 (16)
(16)
Where: each part of this controller is well detailed in [5]. The
design controller is achieved by finding five variables, which are presented by
![]() where the PSO algorithm is used.
Accordingly, the controller tuning parameters are usually carried out by an
optimization process which involves a complex search operation. It may lead to
a wrong controller if an obtained solution is trapped in local minima. To avoid
this problem difficulty, the second contribution of this paper is to propose an
analytical way that reduces the search size of the optimization problem shown
in (15),(16), where the tuning parameters of the proposed robust fractional
controller depend only on three arguments.
where the PSO algorithm is used.
Accordingly, the controller tuning parameters are usually carried out by an
optimization process which involves a complex search operation. It may lead to
a wrong controller if an obtained solution is trapped in local minima. To avoid
this problem difficulty, the second contribution of this paper is to propose an
analytical way that reduces the search size of the optimization problem shown
in (15),(16), where the tuning parameters of the proposed robust fractional
controller depend only on three arguments.
Search space reduction of the optimization problem
A similar procedure given in [15] is used to reduce the variable number of our controller. The proposed idea is summarized as follows:
According to figure 3, if the modelling
error is well minimized (i.e.,![]() ), the open loop
transfer function is determined through the inner loop of figure 3. It yields
), the open loop
transfer function is determined through the inner loop of figure 3. It yields![]() .
.
The main goal is to ensure, by![]() ,
the same characteristic behaviours of the open loop reference model given by
Eq. (17):
,
the same characteristic behaviours of the open loop reference model given by
Eq. (17):
![]() (17)
(17)
Where:![]() , and
, and ![]() are
the new real parameters determined by an adequate optimization algorithm.
According to equation (17), the above proposed fractional order reference model
has two parts:
are
the new real parameters determined by an adequate optimization algorithm.
According to equation (17), the above proposed fractional order reference model
has two parts:
i) The first part
presents the Bode’s ideal transfer function defined by [25]: ![]() ,
,
ii) The second one
corresponds to usual first order transfer function given by: ![]() .
.
In the controller synthesis step proposed by Wang [11], the open loop transfer function of the reference integer model is given by:
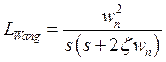 (18)
(18)
Where: ![]() and
and ![]() denote,
respectively, the damping ratio and the natural frequency of the desired open
loop. According to equations (17) and (18), if
denote,
respectively, the damping ratio and the natural frequency of the desired open
loop. According to equations (17) and (18), if![]() ,
and
,
and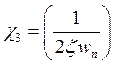 , the Wang’s model becomes a particular
case of our proposed fractional model. Furthermore, if
, the Wang’s model becomes a particular
case of our proposed fractional model. Furthermore, if![]() ,
the ideal Bode’s model becomes also a particular case of our proposition. As a
result, our proposition has the ability of satisfying a more level of imposed
specifications than the one proposed by other synthesis controllers in the
standard SP control strategy. Based on equations (16) and (17), the transfer
function of the proposed robust fractional controller is rewritten as Eq. (19):
,
the ideal Bode’s model becomes also a particular case of our proposition. As a
result, our proposition has the ability of satisfying a more level of imposed
specifications than the one proposed by other synthesis controllers in the
standard SP control strategy. Based on equations (16) and (17), the transfer
function of the proposed robust fractional controller is rewritten as Eq. (19):
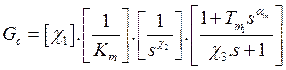 (19)
(19)
Where: the controller parameters are reduced to the three degrees of
freedom![]() , and
, and![]() .
Its optimal values are given by an adequate optimization algorithm, in which
some imposed
.
Its optimal values are given by an adequate optimization algorithm, in which
some imposed ![]() specifications are well satisfied.
specifications are well satisfied.
Fractional-Order SP Controller Based on Optimization Problem
In the robust control theory, the robustness conditions impose certain constraints. These constraints present the magnitudes of sensitivity functions with small values for all frequencies. In addition, the sensor noise and the plant disturbance must have large values
The objective of this issue is to achieve this robustness with minimum magnitudes of the control signal. So, the above conditions are formulated as the following multivariable optimization problem:
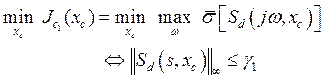 (20)
(20)
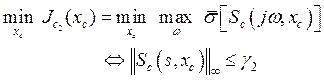 (21)
(21)
![]()
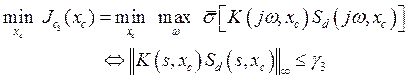 (22)
(22)
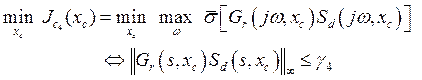 (23)
(23)
Where: Sd and Sc denote, respectively, the
sensitivity and the complementary sensitivity functions, with formula![]() . In addition,
. In addition, ![]() presents
the maximum singular value of the transfer function
presents
the maximum singular value of the transfer function![]() .
Knowing that,
.
Knowing that, ![]() is numerically equivalent to
the infinite norm of Xi(s,xc), Where
is numerically equivalent to
the infinite norm of Xi(s,xc), Where ![]() , with
, with ![]() is
the positive level fixed by the user. In order to avoid the complexity of
calculus, and based on the recent property, we tried to simplify the above
multi-objective optimization problem to a mono-objective one, under
constraints. To achieve this goal, one of the four objective functions (see
equations (20)-(23)) must be selected as the main objective function and the
others are considered as the inequality constraints. Then, we will solve the
obtained optimization problem, using the PSO algorithm [22] to determine the
optimal controller parameters vector, Eq. (24):
is
the positive level fixed by the user. In order to avoid the complexity of
calculus, and based on the recent property, we tried to simplify the above
multi-objective optimization problem to a mono-objective one, under
constraints. To achieve this goal, one of the four objective functions (see
equations (20)-(23)) must be selected as the main objective function and the
others are considered as the inequality constraints. Then, we will solve the
obtained optimization problem, using the PSO algorithm [22] to determine the
optimal controller parameters vector, Eq. (24):
![]() .
(24)
.
(24)
Consequently, the equation ![]() becomes numerically equivalent to
becomes numerically equivalent to![]() , where
, where ![]() is
the positive level fixed by the user.
is
the positive level fixed by the user.
Proposed algorithm for the modelling and the controller synthesis steps
In the modelling step, the fractional model parameters are determined according to the following steps:
Step 1: Choose the set of lower and
upper bounds that limit the design variable![]() , in
which the following condition should be satisfied:
, in
which the following condition should be satisfied: ![]() .
In addition, choose the positive scalar
.
In addition, choose the positive scalar![]() and
go the next step.
and
go the next step.
Step 2: Notice that the ![]() frequency responses of the actual process
frequency responses of the actual process![]() are, usually, available in the world
control society. In this paper, the previous frequency responses are generated using
the Matlab command logspace, in which the
are, usually, available in the world
control society. In this paper, the previous frequency responses are generated using
the Matlab command logspace, in which the ![]() logarithmically
equally spaced points between decades
logarithmically
equally spaced points between decades ![]() and
and![]() can be generated. Set
can be generated. Set![]() and go the next step.
and go the next step.
Step 3: For each ![]() step of the PSO algorithm, the
solution vector
step of the PSO algorithm, the
solution vector ![]() is generated within the range
is generated within the range![]() . Based upon this solution, the
. Based upon this solution, the ![]() frequency responses of the proposed
fractional model
frequency responses of the proposed
fractional model ![]() are determined using equation
(8). Therefore, the cost function of the optimization problem (11) is
determined through the mean absolute error between both gains of the actual
process and the proposed model. However, the inequality constraints of the
optimization problem (11) are determined by the
are determined using equation
(8). Therefore, the cost function of the optimization problem (11) is
determined through the mean absolute error between both gains of the actual
process and the proposed model. However, the inequality constraints of the
optimization problem (11) are determined by the ![]() phases
of the actual process and the proposed fractional model where each obtained
value is compared by the positive level
phases
of the actual process and the proposed fractional model where each obtained
value is compared by the positive level![]() .
.
Step 4: From the previous optimization problem, the new bounded constraints optimization problem is determined using the same idea proposed in [23].
Step 5: The obtained new optimization
problem is solved by the Matlab command particle swarm, which is
available in the Matlab®2015a\toolbox\globaloptim. The syntax of this
command is given by: ![]() , where
, where ![]() is the M-function that defined the
cost function of the bounded constraints optimization problem,
is the M-function that defined the
cost function of the bounded constraints optimization problem, ![]() is the number of the proposed
fractional model.
is the number of the proposed
fractional model.
Step 6: If the stop condition is
satisfied, the algorithm terminates with the optimal solution vector![]() . Otherwise, set
. Otherwise, set![]() and
go back to the step 3.
and
go back to the step 3.
The same previous steps should be followed to determine the robust
fractional controller parameters, in which the optimization problem can be
formulated through equations (20) to (23) where its optimal solution![]() is done by the PSO algorithm.
is done by the PSO algorithm.
In the next section, two actual processes with long dead time will be chosen to validate the proposed fractional controller based upon fractional model for the SP control strategy.
Example 1: Actual process with dead time delay
Considering the actual process defined in [11, 15] by: ![]() , the following numerical data are
chosen in the modelling phase as:
, the following numerical data are
chosen in the modelling phase as:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() and
and![]() .
.
Where: ![]() are, the parameters needed in the PSO
optimization method.
are, the parameters needed in the PSO
optimization method.
Notice that the integer model proposed by Wang in [11], for the same previous process, is defined by Eq. (25):
![]() (25)
(25)
Now, in the synthesis step, the desired robust controller should ensure a good minimization of the sensor noises effect, in which the obtained control signal should be given by a less magnitude. These requirements are formulated as the following constrained optimization problem, Eq. (26):
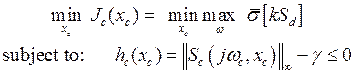 (26)
(26)
Also, the numerical data such as: ![]() ,
, ![]() and
and
![]() are used in the initialization step. On the other side, the
integer order PID controller proposed by Wang in [11] is given by Eq. (27):
are used in the initialization step. On the other side, the
integer order PID controller proposed by Wang in [11] is given by Eq. (27):
![]() (27)
(27)
Example 2: Multiple-lags process
Considering the actual process defined in [11] by: ![]() , the following numerical data are
chosen in the modelling phase as:
, the following numerical data are
chosen in the modelling phase as:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ,
,![]() .
.
Notice that the integer model proposed by Das in [8] is given by Eq. (28):
![]() (28)
(28)
Next, the proposed controller should satisfy a good trade-off between the robust stability and the nominal performances. This goal is formulated as the following optimization problem, Eq. (29):
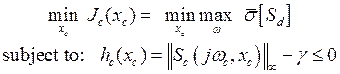 (29)
(29)
To determine the proposed fractional controller, we used the numerical data:
![]() ,
, ![]() ,
, ![]() and
and ![]() in
the initialization step. On the other side, the fractional order PID controller
proposed by Das in [8] is given by:
in
the initialization step. On the other side, the fractional order PID controller
proposed by Das in [8] is given by:
![]() (30)
(30)
Results and discussion
Figure 6 compares the obtained performances given by the proposed fractional model with those given by the integer model of Wang.
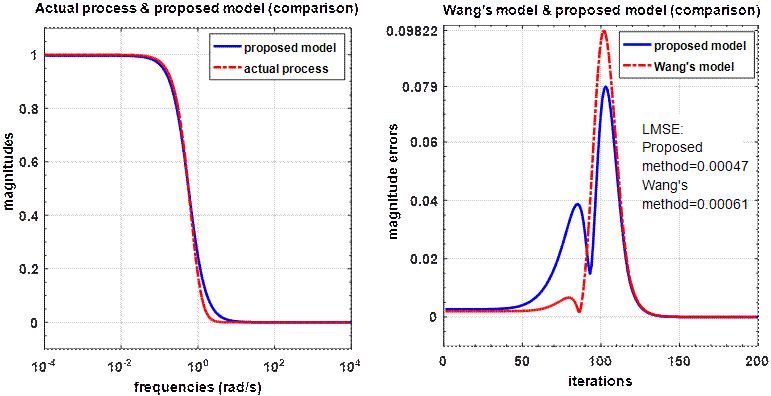
Figure 6. The obtained fractional order model and compared by the Wang's model
The obtained ![]() vector
needed in the transfer function of the proposed
fractional-order model for example 1 is given by equation:
vector
needed in the transfer function of the proposed
fractional-order model for example 1 is given by equation:
![]()
According to figure 6, it can be seen that the proposed
model based on the PSO algorithm ensures a good tracking dynamic to the actual
process in each frequency points. Compared to the Wang's model, the proposed
modelling method ensures a costly value of the maximum error magnitude ![]() and a good minimization of the mean
least square error
and a good minimization of the mean
least square error![]() . Also, the optimal
parameters obtained from running the proposed method are the following
. Also, the optimal
parameters obtained from running the proposed method are the following![]() . These parameters are used to obtain
the proposed fractional order SP controller for example 1. Figure 7 shows the
maximal singular values of both sensitivity functions
. These parameters are used to obtain
the proposed fractional order SP controller for example 1. Figure 7 shows the
maximal singular values of both sensitivity functions ![]() and
and
![]() given by Wang's controller and the
proposed one.
given by Wang's controller and the
proposed one.
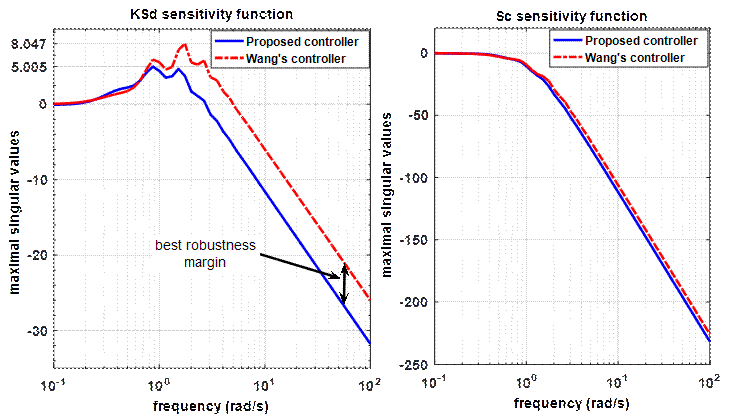
Figure 7. The two sensitivity functions obtained using Wang's method and our proposed one
According to this figure, especially the left side, all
the singular values of the sensitivity function![]() ,
given by the two synthesis methods, are reduced in all frequency points. This
guarantees a proper less control energy. This figure also shows that the
better-obtained sensitivity function is reached when its maximum magnitude
value is small as much as possible, so that the proposed method ensures a
better control signal in the time domain. In addition, it can be seen that,
according to the right side of figure 7, the maximum singular values of the
complementary sensitivity function
,
given by the two synthesis methods, are reduced in all frequency points. This
guarantees a proper less control energy. This figure also shows that the
better-obtained sensitivity function is reached when its maximum magnitude
value is small as much as possible, so that the proposed method ensures a
better control signal in the time domain. In addition, it can be seen that,
according to the right side of figure 7, the maximum singular values of the
complementary sensitivity function ![]() are reduced at
frequencies that are beyond the system bandwidth in order to secure the
robustness at high frequencies. Also, we can see that the better minimization
dynamic of the sensor noises effect is given when the maximum singular values
of the complementary sensitivity function are as small as possible in high
frequencies. As a result, the proposed model controller provides a better
robustness margin. To confirm the above results in the time domain, we use the
following three exogenous inputs on the feedback control system. The first one
represents the set-point reference input
are reduced at
frequencies that are beyond the system bandwidth in order to secure the
robustness at high frequencies. Also, we can see that the better minimization
dynamic of the sensor noises effect is given when the maximum singular values
of the complementary sensitivity function are as small as possible in high
frequencies. As a result, the proposed model controller provides a better
robustness margin. To confirm the above results in the time domain, we use the
following three exogenous inputs on the feedback control system. The first one
represents the set-point reference input ![]() which is assumed as a unit-step
function. The second input represents the load disturbance input
which is assumed as a unit-step
function. The second input represents the load disturbance input ![]() which is assumed as a unit-step function with a gain equal
to
which is assumed as a unit-step function with a gain equal
to![]() , with start-time 40 seconds. Finally,
the third input represents the sensor noise signal
, with start-time 40 seconds. Finally,
the third input represents the sensor noise signal ![]() which
is taken as a Gaussian random distributed form with mean and variance values
are
which
is taken as a Gaussian random distributed form with mean and variance values
are ![]() and
and ![]() respectively
with start-time t = 60 seconds.
respectively
with start-time t = 60 seconds.
Figure 8 compares the obtained performances by the proposed fractional model with those given by the integer Wang’s model.
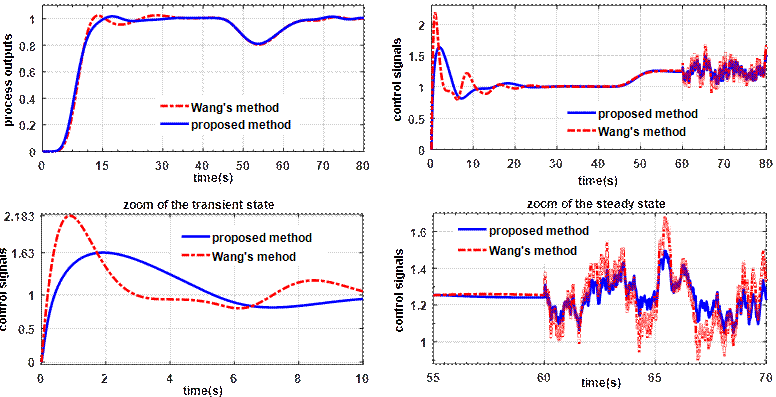
Figure 8. The obtained closed-loop feedback control outputs of the two controllers
From this figure, it is easy to see that the most efficient minimization of the sensor noises effect is ensured by the proposed controller in the steady state. This figure shows also a better control signal with a less magnitude value is guaranteed by the proposed controller in the transient state in which it is not ensured by the other methods.
Now, after running the proposed algorithm to control the
actual process presented in example 2. The optimal ![]() vector needed in the proposed fractional-order model is obtained as follows
vector needed in the proposed fractional-order model is obtained as follows![]() . Also, the optimal parameters vector
. Also, the optimal parameters vector ![]() of
the proposed SP controller (for example 2) is obtained as follows:
of
the proposed SP controller (for example 2) is obtained as follows: ![]() . The obtained performances by the
proposed controller are compared with those given by Das (see Table 1 and Table
2).
. The obtained performances by the
proposed controller are compared with those given by Das (see Table 1 and Table
2).
Figures 9, 10, and 11 compare the closed loop performances given by the proposed fractional controller with those given by the fractional order PID controller proposed by Das.
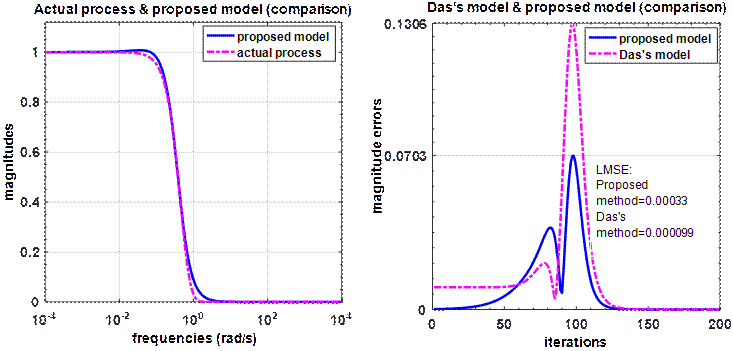
Figure 9.The obtained fractional order model compared by Das's one
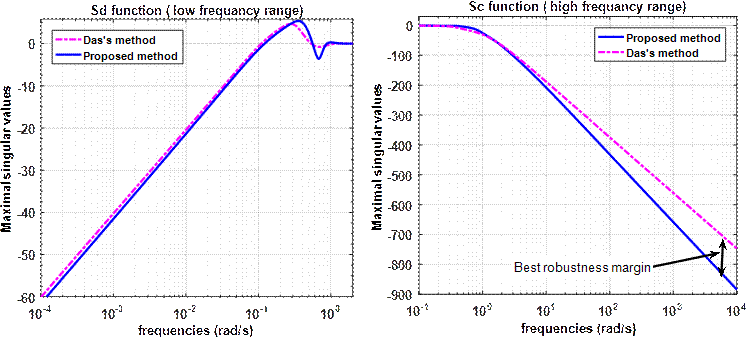
Figure 10. Comparison between the proposed controller and the Das's one in the frequency domain
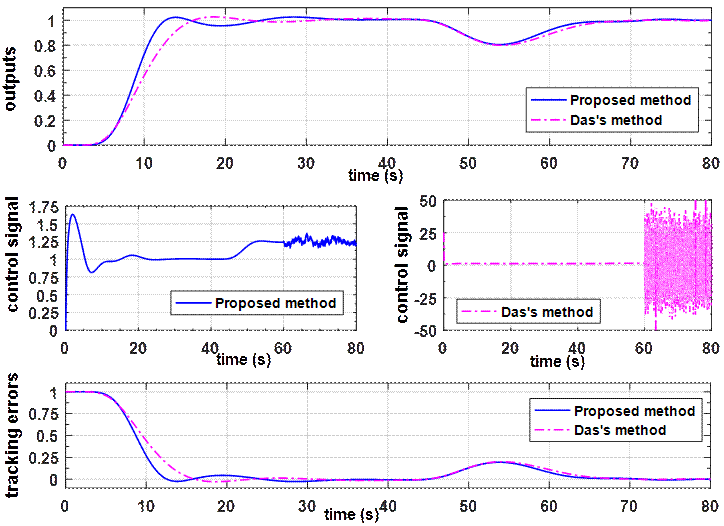
Figure 11.Comparison between the proposed controller and the Das's one in the time domain
Figure 9 compares between both models in the frequency
domain for example 2. It can be seen that the proposed model ensures a good
tracking dynamic of the multiple lags actual process. This result is explained
by a costly value of the maximal error magnitude ![]() and
a better minimization of the least mean square error
and
a better minimization of the least mean square error![]() .
In the second stage, according to figures 10 and 11, it is easy to see that the
proposed controller guarantees the better margin of the stability robustness.
This result is explained in the time domain by a good minimization of the
sensor noises effect in the steady state. To confirm this result, we apply
three exogenous inputs on the feedback control system as follows:
.
In the second stage, according to figures 10 and 11, it is easy to see that the
proposed controller guarantees the better margin of the stability robustness.
This result is explained in the time domain by a good minimization of the
sensor noises effect in the steady state. To confirm this result, we apply
three exogenous inputs on the feedback control system as follows:
The first one is the set-point reference, which is a
unit-step function. The second input corresponds to the load disturbance, which
assumed a step function with amplitude![]() ,
and the start-time is t=40 seconds.
,
and the start-time is t=40 seconds.
Finally, the sensor noise effect signal is chosen as a Gaussian random distributed form, where, the mean and the variance values are respectively, equal to 0 and 0.25, with start-time t=60 seconds. Hence, we can observe that in the steady state, the proposed controller ensures a good minimization of the sensor noise effect. However, in the transient state, the optimal nominal performance is ensured by this proposed controller, where their characteristics are illustrated in table 1 and table 2.
Comparison between the obtained nominal performances by the proposed and the Das's controllers in the transient state (better results are in bold) (Table 1).
Table 1. Comparison proposed and the Das's controllers
|
Indicators |
Proposed controller |
Das's controller |
|
Rise time ( |
5.2297 |
7.7493 |
|
Settling time ( |
63.8253 |
65.5162 |
|
Settling-Min |
0.8049 |
0.7993 |
|
Settling-Max |
1.0253 |
1.0268 |
![]() Table 2. Overshoot and peak time
Table 2. Overshoot and peak time
|
Indicators |
Proposed controller |
Das's controller |
|
Overshoot |
2.4947 |
2.9271 |
|
Peak at time (s) |
1.0253 at (28.4599) |
1.0268 at (18.6034) |
In control systems design, it is often expected to
design a system that has a short rise and settling times, with a small
percentage of overshoot or no overshoot at all. Therefore, according to Tables
1 and 2, it is easy to see that the step response of the closed-loop system
provided by the proposed method has a good time properties in the transient
state, which are a shorter rise time (![]() seconds),
faster settling time (
seconds),
faster settling time (![]() seconds) with less overshoot peak.
seconds) with less overshoot peak.
Conclusions
A new design for a fractional-order controller is proposed combining the Smith Predictor and the fractional reference model. This proposed method is based on the determination of an optimal fractional order model by resolving the proposed bounded constraint optimization problem using PSO algorithm.
In order to satisfy some frequency specifications, a controller synthesis is proposed, where the parameters are obtained by a bounded minimization problem with a reduced search space.
The higher order dead time process has been used to demonstrate the efficiency of the proposed method. The simulation results show that, the proposed controller enhances the performance robustness in both time and frequency domains.
Also, a good tracking behaviour of the set-point references, a good attenuation of the load disturbance dynamic, and a good minimization of both the sensor noises effect, and the energy control cost have been guaranteed.
References
1. Ogata K., Modern Control Engineering. Prentice Hall, Englewood Cliffs, NJ (1990).
2. Giraldo S.A.C., Flesch R.C.C., Normey-Rico J.E., Multivariable greenhouse control using the filtered Smith predictor, J. Control Autom. Electr. Syst., (2016), 27: 349.
Doi: 10.1007/s40313-016-0250-6.
3. Feliu V., Rivas R., Castillo F., Sanchez Rodreguez L., Smith predictor based robust fractional order control. Application to water distribution in a main irrigation canal pool, Journal of Process Control, 2009, vol. 19, no. 3, p. 506-519.
4. Bettayeb M., Mansouri R., Fractional IMC-PID-Filter controllers design for non-integer order systems. J. Process Control, 2014, 24(4), p. 261–271.
5. Bettayeb M., Mansouri R., Al‐Saggaf U., Mehedi I.M., Smith predictor based fractional order filter PID controllers design for long time delay systems. Asian Journal of Control, 2016, 19(2), p. 1–12.
6. Sedraoui M., Boudjehem D.J., Robust fractional-order controller based on improved PSO algorithm for the wind turbine equipped with a doubly fed asynchronous machine, Journal of Systems and Control Engineering, 2012, vol. 226(9), p. 1274 –1286.
7. Vu T. N.L., Lee M., Smith predictor based fractional-order PI control for time-delay processes. Korean Journal of Chemical Engineering, 2014, 31(8), p. 1321-1329.
8. Saptarshi D., Indranil P., Shantanu D., Gupta A., Improved model reduction and tuning of fractional-order controllers for analytical rule extraction with genetic programming. ISA Transactions, 2012, vol. 51(1), p. 237-261.
9. Jesus I., Tenreiro M.J.A., Fractional control with a Smith predictor, J. Comput. Nonlinear Dyn, 2011, 6(3), 031014.
10. Tenreiro M.J.A., Fractional order modelling of fractional-order holds, Nonlinear Dyn., 2012, 70(1), p. 789—796.
11. Wang Q.G., Bi Q., Zhang Y., Re-design of Smith predictor systems for performance enhancement. ISA Transaction., 2000, vol. 39(1), p.79-92.
12. Normey-Rico, J.E., Sartori, R., Veronesi, M., Visioli A., An automatic tuning methodology for a unified dead-time compensator. Control Engineering Practice, 2014, 27, p. 11–22.
13. Tenreiro M.J.A., Optimal tuning of fractional controllers using genetic algorithms. Nonlinear Dyn, 2010, 62(1--2), p. 447—452.
14. Zhuang M., Atherton, D.P., Automatic tuning of optimum PID controllers. In IEE Proceedings D-Control Theory and Applications, 1993, 140(3), p. 216-224.
15. Zhang W., Xu X., Analytical Design and Analysis of Mismatched Smith Predictor. ISA Transactions, 2001, vol. 40(1), p. 133-138.
16. Palmor Z.J., Blau M., An Auto-Tuner for Smith Dead Time compensator. International Journal of Control, 1994, vol. 60(1), p. 117-135.
17. Hang C.C., Wang Q.G., Cao L.S., Self-Tuning SPs for Processes with Long Dead Time, International Journal of Adaptive Signal Process., 1995, vol. 9(1), p.255—270.
18. Kaya I., Obtaining controller parameters for a new PI-PD Smith predictor using auto tuning. Journal of Process Control, 2003, vol. 13(1), p. 465—472.
19. Baiyu O., Lei S., Chunlei Ch., Tuning of Fractional PID Controllers by Using Radial Basis Function Neural Network. In: 8th IEEE international conference on control and automation, 2010, p.1239-1244.
20. Monje C.A., Vinagre B.M., Feliu V. et al., Tuning and auto-tuning of fractional order controllers for industry applications. Control Engineering Practice, 2008, vol. 16 (7), p. 798--812.
21. Jabri K., Dumur D., Godoya E., Mouchetteb A., Béleb B., Particle swarm optimization based tuning of a modified smith predictor for mould level control in continuous casting. Journal of Process Control, 2011, vol. 21 (1), p. 263—270.
22. Clerc M., Kennedy J., The particle swarm explosion, stability and convergence in a multidimensional complex space. IEEE Trans. Evolut. Comput., (2002), 6: 58-73. DOI 10.1109/4235.985692.
23. Maruta I., Hyoung T., Sugie T., Fixed-Structure Controller: A Meta-Heuristic Approach Using Simple Constrained Particle Swarm Optimization. Automatica, 2009, vol. 45(1), p. 553-559.
24. Aoun M., Malti R., Levron F., Oustaloup A., Synthesis of fractional Laguerre basis for system approximation, Automatica, 2007, 43(9), p. 1640-1648.
25. Ramiro S., Barbarosa S., al. Tuning of PID Controllers Based on Bode's Ideal Transfer Function. Non-Linear Dynamic Journal, 2004, vol. (38), p. 305-321.