Engineering,
Environment
Neuron network application
for speed control and fault detection of asynchronous machine
Kheira MENDAZ1, Houria
BOUNOUA2, Aicha TOUHAMI3
1,3 University Centre Belhadj
Bouchaib Ain Temouchent, Electrical engineering department, Ain Temouchent, 46000, Algeria
2Djillali Liabes University, School of Engineering
Sciences, IRECOM Laboratory, Electrical Engineering department, Sidi Bel Abbes,
22000, Algeria
E-mail(s): 1kheiramendez@gmail.com, 2
hsemmach@yahoo.fr, 3 touhami_aicha@yahoo.com
* Corresponding author, Phone: +2130799006615
Received: July
05, 2017 / Accepted: December 27, 2017 / Published: December 30, 2017
Abstract
The induction machine will play a role very important in the industry,
but the existence of a certain defect returns their use limited as the defects
rotor (broken bar). This article presents a study of Controller neuronal with
the existence of a rotor defect on the one hand and another hand of a defect of
switch of the five levels inverter to see the influence of these two defects on
the physical parameters of the machine. The
application of neural control with the existence of a broken bar in the motor
allows us to see the effect of this fault on the motor parameters (speed,
electromagnetic torque and current), to control itself is also used in
existence of five-level inverter fault (delay of blocking the switch) to give the
results shown the swelling of this fault on the engine. With this controller,
each fault influenced the parameters of Engine and can notice it from the
simulation results.
The results, simulations are done using
Matlab/Simulink. Simulation results show clearly and robustness of neural
controller.
Keywords
Induction machine; Rotoric faults; Broken
bar; Five levels inverter; Switch fault; Neural controller
Induction motor is widely used in the industrial applications and is a
very important part to support industry in the manufacturing
process due to its low cost, easy operation and simple maintenance.
However, in recent years the induction motor drives have been able to be used
in variable speed applications with the rapid development.
There are various faults occurring in the induction machine (IM) such as broken
rotor bar fault. Motor
rotor faults are caused by a combination of
various stresses that act on the rotor. The broken rotor bar is a common fault
of the motor rotor [1]. It can be caused by the following reasons: (1) Thermal
stresses due to thermal overload and unbalance, hot spots, or excessive losses,
sparking; (2) Magnetic stress caused by electromagnetic forces, unbalanced
magnetic pull, electromagnetic noise, and vibration or residual stresses due to
manufacturing problems [2].
The neural network
(ANN) is widely used as a universal approximates in nonlinear mapping and
uncertain nonlinear control problems. Neural control is very powerful tool
capable of achieving very good results in the control of complex systems. It is
preferred to use neural networks (ANN) for control when requirements for
precision are high and system is not identified precisely or its parameters are
changing [3, 4, 5].
This article discusses two studies: the first is the use of a neural
speed regulation with the existence of a rotor defect (broken bars) and then an
addition to this regulator a neural detection of
rotor broken bars, concerning the secondly, it is the application of a
neural speed regulation, but this time for an existence of a defect at the five-level
inverter (switch faults), after adding to this regulator a neural detection of
switch fault. The first part we used the neural speed regulator with an existence of a rotor defect of the induction machine that
allows us to have an improvement of signal quality of speed, torque and
currents (no overshoot, reduction of rise time) with
modulation of these signals at the time of application of faults, and then goes
on to use this neural speed regulator with a neural detection of rotor broken bars which gives a signal
quality performance and at the same time can notice a ripple only at the time
of fault application. In the second part uses a neural speed regulator, but
this time we apply a switch fault at five-level inverter which gives a certain
result which shows the influence of these defects on the physical parameters of
the machine, after we add to this regulator a neural detection of switch fault
to receive a result more preferment. [6]. Result simulation using Matlab shows
the effect of this controller.
Material and method
In this section we present the model of the asynchronous machine with a rotoric defect (broken bar) which will be in combination of a
five level inverter contains a switch fault, first we used a neuronal speed
controller for the improving response time and system
stability with the existence of these defects, the application of this
controller allows to notice the effect of these faults on the physical
parameters of the asynchronous machine, then we let us add a neural detector
fault (neural detector of broken bar fault on the one hand and on the other
hand a neural detector inverter fault) to the neuronal speed controller with
the presence of these defects, which shows more performance
results can be seen in the imbalance and perturbations which attracts the
physical parameters of the machine at the moment of defect.
Mathematical modelling of the
induction motor
The model of the induction motor is derived by using
d and q variables (Park model) in a synchronous rotating reference frame, can
be represented by Eq. (1):
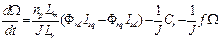 (1)
(1)
Where: Ω - the rotor speed; np - is the quantity of poles pair; Lr - rotoric inductance;
Lm - mutual inductance; ɸrd - arm of the flux generated by the rotor on the axes d; ɸrd - arm
of the flux generated by the rotor on the axes q; Isd - current on the axes d; Isq - current on the axes q; J - inertia of rotor; f - is the friction of the rotor; Ce - torque of induction machine; Cr
- load of induction machine.
The current
equation Isd, its
expression is given by Eq. (2):
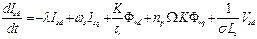 (2)
(2)
Where: Vsd -
the stator voltage on the axes d, ωs – statoric pulsation ; K –positive constant
equal to the report of the mutual inductance on statoric inductance multiplied
by rotoric inductance and Blondel coefficient ; τr - rotor time constant;
σ – Blondel coefficient ; Ls – statoric induction; λ- constant is the
relation between the Blondel coefficient and the constant of stator and rotor
time.
The equation for the constants used in Eq. (2), is given by Eq. (3-4):
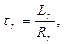
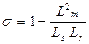 ,
, 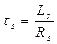 (3)
(3)
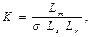
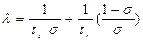 ,
, 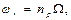 (4)
(4)
Where: Ls - statoric inductance,
τs - stator time constant, ԝr - the pulsation of the rotor field, Rs - statoric resistance,
Rr - rotoric resistance.
The current equation Isq is given as Eq. (5):
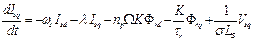 (5)
(5)
Where: Vsq
- rotor voltage on the axes q; ԝs - statoric pulsation.
We can get the rotoric flux equation in the axes (q-d) is given by using the Eq. (6-7):
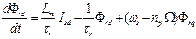 (6)
(6)
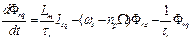 (7)
(7)
The
rotoric fault model of the induction machine
It is necessary to develop a model of
rotoric fault that explains the disequilibrium who transit a minimum of parameters [7-9], these
parameters must be the image of the fault presented in the machine. The figure 1 illustrated the conventional modelling of the rotor.
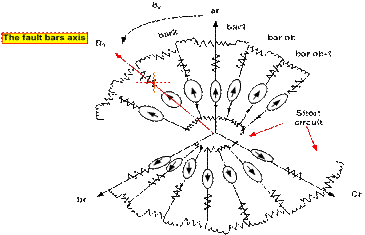
Figure
1. Modelling of elementary dipoles for
rotoric fault
The detection, fault of broken bars of the induction machine can be obtained
by the dynamic model
developed in a stationary reference frame (d-q) that was given by the following Eq. (8-9):
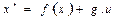 (8)
(8)
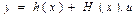 (9)
(9)
Where: x*-
state equation
With the
state vector and the input vector, Eq. (10):
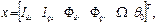
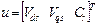 (10)
(10)
Where: x - is the state vector, u- the input
vector
With the output vector, Eq. (11):
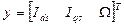 (11)
(11)
Where: y- the output vector.
The state matrix, Eq. (12):
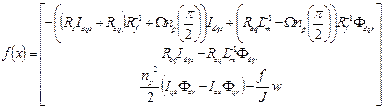 (12)
(12)
Where: f(x) -
state matrix, Req - the resistance equivalent to the rotor, is the series
connection of the sound rotoric resistance Rr and a fault resistance Rf.
The command matrix, Eq. (13):
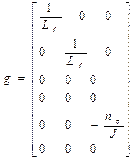 (13)
(13)
Where:
g - is the command matrix; h(x)
- output matrix.
The resistance equivalent to the rotor and the fault resistance, Eq.
(14-16):
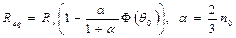 (14)
(14)
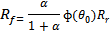 (15)
(15)
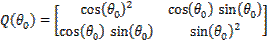 (16)
(16)
Where: Q (θ0) – defect matrix; θ0 - the angle indicating the defect; n0 - reported defect equal
to the report of the number of faulty turns on the total number of turns in a
fictitious three-phase rotor phase without defect; ɸ (θ0) - flux
which is a stationary magnetic field with in the report to the rotor and is
directed along the axis θ0.
Structure of the five levels inverter
associated with induction machine
In order to go up in voltage and power, the conventional inverter on two
levels starts with uses replaced by the inverters multi levels in the
industrial applications most varied, requiring a great power. The judicious
exploitation of the point medium of the continuous source appreciably improves
quality of the wave of voltage with dimensions receiver what is advantageous to
reduce the pulsating torque and the losses in the induction machines [10].
An advantage
which rises from this structure consists with the best controls constraints in
the components voltage, the amplitude of the terminal voltage is limited to the
half voltage of the source raised of has overpressure due to the commutation of
the switches.
This topology can generate a simple voltage on five levels [11-12]
(between the arm of inverter and the point medium). In this paragraph, we study
the structure of the inverter to five levels (Figure 2).
This structure is composed of three symmetrical arms consisted each of
six switches of series and two others in parallels G7 and G8. More two diodes,
noted D9, D10 allowing obtaining level zero of the voltage Vk0 (k=R, S, T).
Each one of these switches is composed of a semiconductor bi-controllable and
of a diode assembled in teat digs.
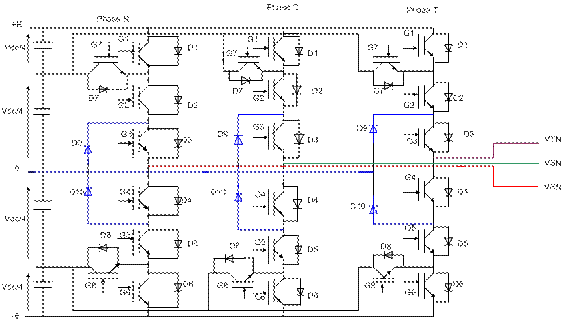
Figure 2. The five levels
inverter structural
In order to avoid short-circuits of the sources voltage [13], and to have
a continuous conduction, therefore an operation completely controllable one adapts a complementary order
definite as follows:
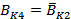
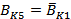
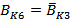
Where: BKS=
[Gk-Dk] is IGBT with anti-parallel
diode for the
arm k (k=R, S, T); Ki=1: Show the closed of high switch
and opened of law switch; Ki=0: Show the open of high switch and closed of law
switch.
Diagnostics faults of seven levels inverter
In the inverter five level, the voltage of phases has fifteen levels
under symmetrical functional, but their levels of voltage seem to be different
with each fault from commutation. The voltage of phase for the positive period
has only five levels because the current of phase crosses the K17
switch instead of k11 in the state of P (positive) [12]. In the
event of fault of commutation of k12, the voltage of phase for the
positive period has only three levels because the current of phase crosses the
K13 switch in the state of P (positive). Consequently, when each
fault of commutation occurs, the voltage of fictitious phase differently
appeared between them.
The fault of K17 and k12
induces disequilibrium in the three phases [10-13], which translates by the
discharge of the lower condensers of the arm R of the inverter five levels.
K12: the switch
of first arm (phase R) composed for [G2, D2].
K11: the switch of first arm (phase R) composed for [G1, D1].
K13: the switch of first arm (phase R) composed for [G3, D3].
K17: the switch of first arm (phase R) composed for [G7, D7].
K18: the switch of first arm (phase R) composed for [G8, D8].
G1, G2, G3,
G4, G5, G6, G7, G8, G9, G10 are insulated-gate bipolar transistor
(IGBT), and D1, D2, D3, D4, D5, D6, D7, D8, D9, D10 are freewheel diode.
Construction of neural network
Supervise techniques
for neural networks are based on the existence of a database of training data
[4], from which one seeks to find a relationship between the input variables
and output variables. From these input variables, the neural network provides a
response characterized by two types of output variables [14-15-16].
Actual output
variables which can represent an estimate of the supervise parameter or output
categorical variables that represent the state of functionality equipment [4].
The type of neural
network application in the supervise domains is related to the nature of the
output data.
Determining the
neural model for the identification is an essential phase [7-8], which may be more or heavy months of executing the
industrial diagnosis.
The algorithm allows
us to select the robust neural model [17-18], for
identification will be aspiring in the following steps:
1.
The knowledge
about the system to be identified;
2.
Chosen of the
inputs and outputs of the neural model;
3.
Determination of
the internal behaviour of the number of neurons in each hidden layer;
4.
Chosen of
activation functions;
5.
Chosen of
accuracy and the number of iteration.
Speed regulation with neural network
The Figure 3 illustrated the
application of neural network controller that use for speed control, the
algorithm of back propagation to use it is gradient [7,15-16].
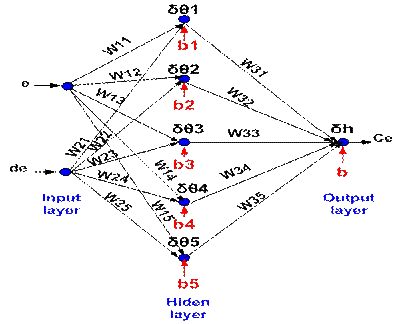
Figure
3. Multilayer perceptron, structural (2, 5, 1)
The figure represents the input layer
which is made up of two neurons the error and the derivative of the error, so
the hidden layer which consists of five neurons and the output layer of only
one neuron that couples [19-21].
Back propagation of gradient
The functions defining
the output neuron are presented by the following equations, Eq. (17, 19, 21, 23,
25, 27):
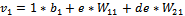 (17)
(17)
Where: v1 -
the function defined by the output neuron, which
realizes a scalar product between the weight and input value with the addition
of bias; W11
- weight of input
layer
for first neuron; W21 - weight of input layer for second neuron; e - the error of the first input neuron,
is the difference between the value of the desired output d and the present
value of the output of the neuron Ce; de - error derivative of second input
neuron;
b1 - biais of first neuron in the hidden layer.
The activation functions that determine the output of the
first neuron from the input layer and the second neuron from the input layer
are presented by the following equations, Eq. (18, 20, 22, 24, 26).
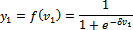 (Sigmoid function) (18)
(Sigmoid function) (18)
Where: δ- Degree of
nonlinearity = 1; y1 - activation
function that determines output between the first neuron in the input layer and
the second neuron in the input layer.
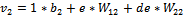 (19)
(19)
Where: v2 - is
the function defined by the output neuron; W12 - weight of the input
layer of the first neuron in the input layer; W22 - weight of the
input layer for the second neuron in the input layer; b2 - biais of the second neuron for hidden layer.
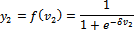 (20)
(20)
Where: y2 - is the activation function that determines output between the first
neuron of input layer and the second neuron of the input layer.
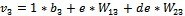 (21)
(21)
Where: V3 is
the function defined by the output neuron, W13 - weight of the input
layer of the first neuron in the input layer, W23 - weight of the input
layer of the second neuron in the input layer, b3 - biais of third neuron in the hidden
layer.
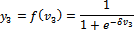 (22)
(22)
Where: y3 - is the activation function that determines output between the first
neuron of input layer and the second neuron in the hidden layer.
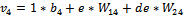 (23)
(23)
Where: V4 is
the function defined by the output neuron, W14 - weight of the
input layer of the first neuron in the input layer, W24 - weight of the input
layer for the second neuron in the input layer, b4 is the biais of fourth neuron in the hidden
layer.
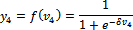 (24)
(24)
Where: y4 - the activation function that determines output between the first
neuron of input layer and the second neuron in the hidden layer.
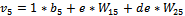 (25)
(25)
Where: V5 - the
function defined by the output neuron; W15 - weight of the
input layer of the first neuron in the input layer; W25 - weight of the
input layer of the second neuron in the input layer; b5 -biais of the fifth neuron in the hidden
layer.
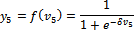 (26)
(26)
Where: y5 - is the activation function that determines output between the first
neuron of input layer and the second neuron in the hidden layer.
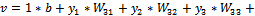
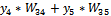 (27)
(27)
Where: v -
the function defined by the output neuron; W31- weight of the
input layer of the first neuron in the hidden layer, W32 - weight of the input
layer of the second neuron in the hidden layer, W33 - weight of the
input layer of the third neuron in the hidden layer W34 is the weight of the
input layer of the fourth neuron in the hidden layer, W35 - weight of the
input layer of the five neuron in the hidden layer, b-biais of output neuron in the output
layer.
The activation function that determines the output between
the all neuron in the hidden layer and the neuron in the output layer is
presented by Eq. (28, 29, 31):
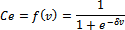 (28)
(28)
Where: Ce - is the activation function that determines output between the all
neuron in the hidden layer and the neuron in the output layer.
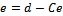 (Error) (29)
(Error) (29)
Where:
d-Desired
value.
The error gradient is presented by Eq. (30, 32-36):
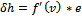 (Gradient) (30)
(Gradient) (30)
Where: δh - is the
error gradient for neuron in the output layer
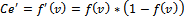 (31)
(31)
Where:
Cé́ʹ is
the derivative
activation function
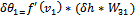 (32)
(32)
Where:
δθ1
is the error gradient of the first neuron in the hidden layer, fʹ (v1) - derivative activation function.
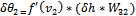 (33)
(33)
Where:
δθ2
is the error gradient of the second neuron in the hidden layer, fʹ (v2) - derivative activation function.
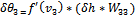 (34)
(34)
Where:
δθ3
is the error gradient of the third neuron in the hidden layer, fʹ (v3) - derivative activation function.
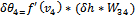 (35)
(35)
Where:
δθ4
is the error gradient of the fourth neuron in the hidden layer, fʹ (v4) - derivative activation function.
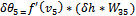 (36)
(36)
Where:
δθ5
is the error gradient of the fifth neuron in the hidden layer, fʹ (v5) - derivative activation function.
The structural multi-layer perceptron used in the neural network of the
asynchronous machine for detection of broken bars for one hand and in other
hand for detection of switch fault of five levels inverter is given in Figure
4.
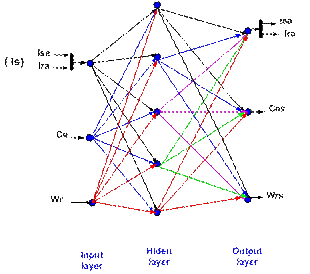
Figure 4. Multilayer perceptron,
structural (3, 5, 3)
Where: Ce - input electromagnetique torque of neural network;
Wr - input measured speed of neural network; Is (Isa, Ira) - input statoric,
rotoric current of neural network; y - output neural, (x1, x2… xn) are the
inputs neural, (w1, w1… wn) the correspondence heaviness, b is bias of neuron.
After the upload of the output and
input, we created a neural network of three layers (two input layers, one
output layer and five hidden layers), by the utilization of Matlab “newff”
function, and the chosening of learning function “trainlm”. However, if the
neural network is constructed and the learning afflicted the satisfactory
performances, we utilized the Matlab function “train” and simulated the results
(utilization of Matlab function “sim”).
In the first regulator neural network, the error speed (Wref-Wr)
is the input of neural network, and the electromagnetic torque (Ce) is the output of neural network, this
controller use for speed control.
In the second controller neural network, in our model of induction machine, the
speed Wr, electromagnetic torque Ce and the statoric, rotoric current Is
are the inputs of neural network, and the (Ces, Wrs,
Isa and Ira) are the outputs of neural network which
designated the value (0 0 1 0), so the corresponding fault: broken bars (0:
there is not a fault; 1: induces of fault).
The Figure 5 shows the model of the asynchronous machine in the Park
reference (dq) associated with a five-level inverter with the application of
the command field oriented control (FOC), or also the use of a neural speed
controller (RNA1), thus the second neural controller for the detection of rotor
faults (bar breaking) on the one hand and, on the other hand, for the detection
of faults in the inverter (switch fault) which is named by RAN2.
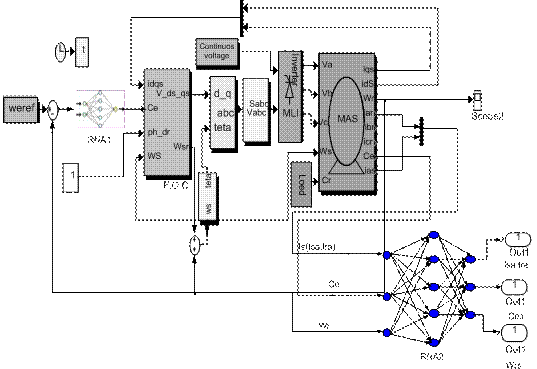
Figure
5. Command of induction machine with application of regulator neural
network
Results and discussion
The Figure 6 shows the position of
neural.
In the Figure 6 (a) shows the
position of the neurons used in the speed control of the asynchronous machine
we used position (1, I) which shows the input layer which contains two neurons,
the hidden layer consisting of five neurons and the output layer that will have
a neuron saddle, or maybe even the connection between the input layer and
hidden layer and thus the hidden layer and the output layer.
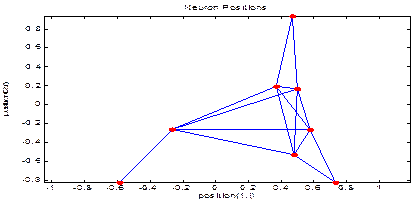
(a)
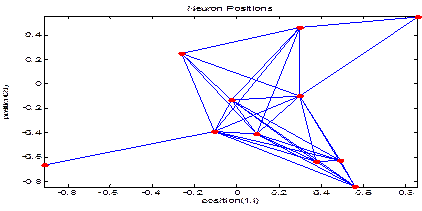
(b)
Figure 6. (a) Neuron position for the first; (b)
Second neural controller
Figure 6 (b) shows the position of the neurons used in the second
controller for fault detection (bar fault and inverter switch), we have taken
positions (1, I) which shows the connection between the input layer (Three
neurons) layer hidden (five neurons) and so the connection between hidden layer
and output layer (three neurons).
Bars fault
The simulation was elaborated on Matlab/Simulink for the induction
machine associated with five levels inverter. For showing the effect of broken
bars on induction machine with utilization of neural network controller (show
the effect of the broken bars on simulated vectors: speed (Wr),
electromagnetic torque (Ce) and the statoric and rotoric current Isa,
Ira), and the effect of switching fault for the inverter on the simulated vector for the
induction machine. The type of fault that we study is the
broken bars of the cage asynchronous machine.
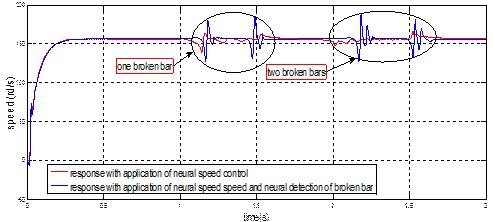
Figures 7-8
represent the characteristics of the sound machine with existence of fault
rotoric (one broken bar at t= (1s, 1.5s) and two broken bars
at t=(2s, 2.5))
with application of neural speed control and application of neural speed regulation control with neural
detection of rotor broken bars.
(a)
(b)
Figure 7. (a) Speed, (b) Electromagnetic
torque result of induction machine
In the figure 7(a) we
observe a slight modulation disturbs the evolution of speed when the first bar
is broken at t =
(1s, 1.5s). We also note that this modulation becomes more
important with the advent of the second fault at t=(2s, 2.5s).
In theory, this amplitude modulation is identical to the speed, frequency 2gf but as we can see,
it is relatively difficult to discern with a simple visual analysis. The
figure 7 (a) with application
of two neuronal controller (neural speed control and neural detection of broken
bar) during the rotor defect we remark a disturbance on the speed.
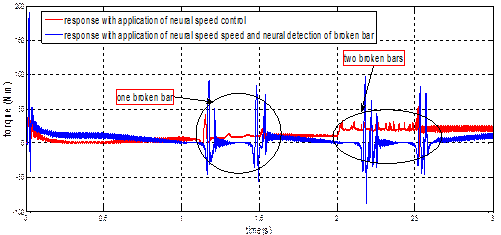
In the figure 7 (b)
the analyses of the electromagnetic
torque with application of speed neural control show a significant change in
its appearance when rotor faults occur. The presence of an oscillation, when
there is a rotoric fault of the machine, is due to the consideration of space
harmonics in the model. In figure 7(b), the application of neural speed control and neural detection of broken
bar during the rotor defect (broken bars), the electromagnetic torque
signal show the oscillation at the time of one broken bar
, this oscillation become more at the time of two
broken bars.
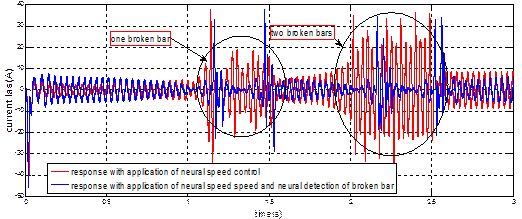
(a)
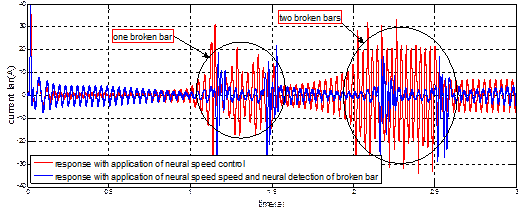
(b)
Figure 8. (a) The current Isa;
(b) Ira result of
induction machine
In the figure 8 (a) we note that the first broken bar indicates a more
perturbation in the statoric current during the
application only of the neuronal speed controller. But
the use of two controllers (neural speed control and neural detection of broken bar) at
the same time shows a very small increase in this current. The Figure 8 (b) and
concerning the rotor current there exists on their signals the undulations and
oscillations during the two defects.
The application of neural speed regulation with neural
detection of rotor broken bars gives the performance result compared with the application of neural
speed regulation.
Inverter fault
The figure 9,
from the switch fault K12 of five levels inverter with application of neural
speed control, we notice the voltage unbalance during the fault.
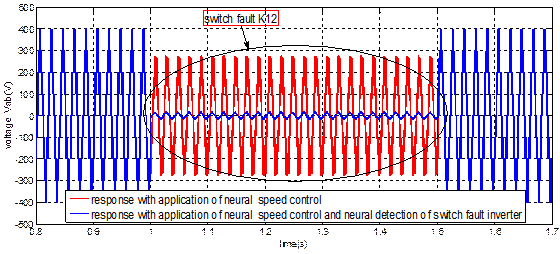
Figure 9. Voltage
results Vab of five levels inverter with switch fault K12
at t (1s, 1.5s)
Unlike the use of two controllers (neural
speed control and neural detection of a switch fault inverter) which
shows the disequilibrium voltage during the fault, that notice how the faults
of this switcher K12 induce a disequilibrium on these voltages.
(a)
(b)
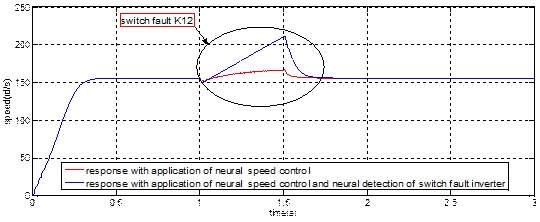
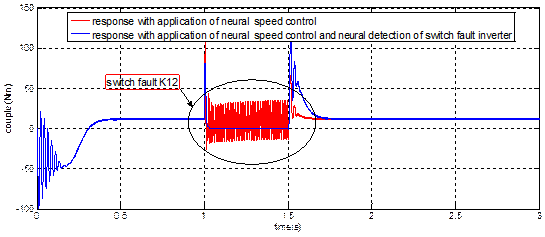
Figure 10. (a) Speed,
(b) Electromagnetic torque results of induction machine
In the figure 10 (a), the use of neural speed control during the
existence of a defect switch K12 at t (1s, 1.5s) of the inverter five level
show the effect of this fault on the physical parameters of the induction
machine which are translated by an increasement of speed, this increasement
become important with application of two controllers.
But the Figure 10 (b) with application of a neuronal speed controlled
during the fault switch K12 allows us to see more ripples on the
electromagnetic torque signal, unlike the application of two controllers which
shows the cancellation of this signal during the fault.
(a)
(b)
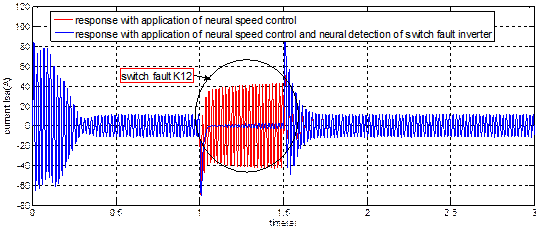
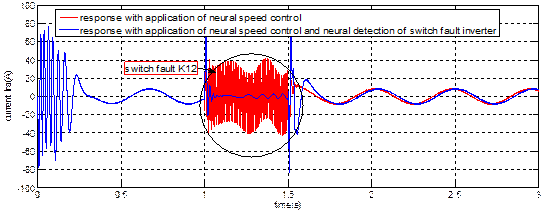
Figure 11. (a) Current result Isa,
(b) Current result Ira of induction machine
The figure 11 (a)
and with the application of neural speed
control
during the switch fault K12 at t (1s, 1.5s) induces disequilibrium on the
currents Isa which can be seen by the undulation which disturbed the
signal during the fault, but the application of two controllers (neural speed control and neural detection of a switch
fault inverter) shows a different result when can noticed by the
current cancellation during the fault.
In the figure 11 (b),
it is possible
that the same results can also be noticed on the rotoric current Ira which is
disturbed during the switch defect K12 when applying only a neuronal speed
controller and the cancellation of current at the time of default using two
controllers (neural speed control and
neural detection of switch fault inverter).
If they have a production of the fault in the five levels inverter, the
current deporting in the medium point caused a
ground effect on the charge/discharges
condensers variation.
The fault in high switchers, produce an increase in lower discharges condensers, and the voltage level appears to be
different for each switching fault, this disadvantage of five levels inverter
has an influence on the induction machine.
Conclusions
Each of these two controller that we presented (neural speed controller, neural
speed controller with neural detection of broken bar for one hand and in other
hand neural speed controller with neural detection of switch fault inverter)
for a rotor fault existence or for a defect of switch of the five levels
inverter gives results different, but performance,
each regulator enables us to have the influence of the existence of a defect on
the physical parameters of the induction machine (speed, electromagnetic couple
and the two stator current and rotor) which is in the undulation and the
oscillation which disturbed various signals, Two controllers neural speed and neural speed with
neural detection of broken bar show the bar breaking effect, or see the undulation
on the speed, the torque and the stator, rotor currents oscillation of the asynchronous
machine. Contrary to the detection of the switch faults five-level inverter,
after using a neuronal speed controller with a neuronal detection of switch
faults five-level inverter noticed that the results show the cancellation of torque, elevation of The speed and
oscillation of the currents during the application of fault, comparing to the
use of a neuronal controller speed only by noticing that the speed is raised
more, the torque and the current will be more undulating, its enables us to
conclude deterioration and damage system for the presence of these defects.
References
1.
Hsu J.S., Monitoring
of defects in induction motors through Air-Gap torque observation, IEEE Transactions on Industry
Applications, 1995, 31 (5), p. 1016-1021.
2.
Bellini A.,
Filippetti F., Quantitative evaluation of induction motor broken bars by means
of electrical signature analysis, IEEE Trans. On Industry Applications, 2001,
37 (5), p. 1248-125.
3.
Khammar F.,
Debbache N.E., Application of artificial intelligence techniques for the control
of the asynchronous machine, Journal of Electrical and Computer Engineering,
2016, 1 (1), p. 1-11.
4.
Julien M.,
Reconnaissance des défauts de la machine asynchrone application des modèles
d’intelligence artificielle, Doctoral Thesis in information science and
Technology, University Québec, Chicoutimi, 2017, p. 245-251.
5.
Hammoumi A.,
Massoum A., Meroufel A., Wira P., Application de réseaux de neurons pour la
machine asynchrone sans capteur mécanique, Acta Electrotechnica, 2012, 53 (2),
p. 99-104.
6.
Kowalski G.T.,
Orlowska K.T., Neural networks application for induction motor faults
diagnosis, Mathematics and Computes in Simulation, 2003, 3 (5), p. 435-448.
7.
Kanika G.,
Arunpreet K., Devender K., Induction machine rotor faults diagnostics through stator
current using artificial neural network, International Journal of Emerging
Trends and Technology in Computer Sciences, 2014, 3 (4), p. 13-21.
8.
Ebrahimi M.,
Rezaei E., Vaseghi B., Danesh M., Rotor resistance identification using neural networks
for induction motor drives in the case of insensitivity to load variations,
Iranian Journal of Science & Technology, Transaction B, Engineering, 2006,
30 (B2), p. 223-236.
9.
Tian H., Bo-Suk
Y., Won-Ho C., Jae-Sik K., Fault diagnosis system of induction motors based on neural
network and genetic algorithm using stator current signal, International
Journal of Rotating Machinery, 2006, 1 (1), p. 1-13.
10. Mendaz K., Bounoua H., Felliti M.,
Comparative study of diagnostic of inverter three and five levels associated
with asynchronous machine, International Journal of Science and Research
(IJSR), 2013, 2 (9), p. 385-389.
11. Seguier G., Labrique F., Les
convertisseurs de l’électronique de puissance, technique et
documentation-Lavoisier, 1989.
12. Ouhid B., La contribution de
l’analyse des onduleurs multi niveaux, mémoire de magister, 2005.
13. Mendaz K., Bounoua H., Felliti
M., Diagnostic of inverter three levels associated with asynchronous machine,
International Journal of Engineering Research and Technology IJERT, 2013,
2 (9), p. 3101-3106.
14. Deepa C., Arulmozhiyal K., Optimized neural
network based speed control of sensor less induction motor, International
Journal of Micro and Nano Systems, 2011, 2 (1), p. 59-63.
15. Taifour A., Abdelaziz Y.M.A., Ekram
H.A.O., Control of induction motor drive using artificial neural network,
Journal of Engineering and Computer Science, 2014, 15 (2), p. 1-7.
16. Moradian M., Ebrahimi M., Danesh M.,
Bayat M., Detection of broken bars in induction motors using a neural network,
Journal of Power Electronics, 2006, 6 (3), p. 245-252.
17. Ibrahim M.M., Nekad H.J., Broken bar fault
detection based on the discrete wavelet transform and artificial neural network,
Asian Transactions on Engineering, 2013, 3 (2), p. 1-6.
18. Babhale N., Jawadekar A., Application
of cepstrum and neural network for induction motor fault diagnosis,
International Journal of Electrical, Electronics and Data Communication, 2017,
5 (2), p. 50-54.
19. Pu S., Zheng C., Yuriy V., Fault
detection and diagnosis of induction machines based on wavelet and
probabilistic neural network, International Journal of Computer Applications,
2013, 69 (14), p. 44-50.
20. Rijaniaina N.A., Modélisation du
défaut d’excentration dans une machine asynchrone. Application au diagnostic et
à la commande de deux machines spécifiques, doctoral Thesis in electrical
Engineering, University Henri Poincaré, Nancy I, 2009, p. 125-140.
21. Bachir S., Trigeassou J.K., Tnani S.,
Cauet S., Diagnostic des défauts statoriques et rotoriques par identification
paramétrique sans capteur de vitesse, International Conference of Francophone
Automatic, Nantes, 2002, p. 447-452.
![]() (1)
(1)![]() (2)
(2)![]()
![]() ,
, ![]() (3)
(3)![]()
![]() ,
, ![]() (4)
(4)![]() (5)
(5)![]() (6)
(6)![]() (7)
(7) 
![]() (8)
(8) ![]() (9)
(9)![]()
![]() (10)
(10)![]() (11)
(11)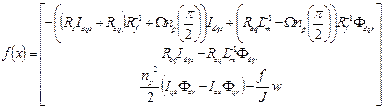 (12)
(12)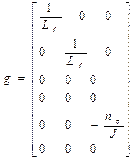 (13)
(13)![]() (14)
(14)![]() (15)
(15)![]() (16)
(16)













