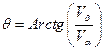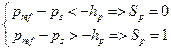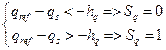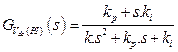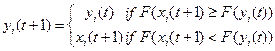Engineering, Environment

Optimization of direct power control of three-phase shunt active power filter by using PSO algorithm

Mohamed Rida BENGOURINA¹*, Mostefa RAHLI¹, Saadi SLAMI², Linda HASSAINE³

¹ Laboratory LORE, Faculty of Electrical Engineering, University of Science and Technology Oran, Algeria

² Sciences and Technology Faculty University of Djelfa, Algeria

³ Centre de Développement des Energies Renouvelables (CDER), Algeria

E-mail(s): ¹bengourina.rida@yahoo.fr; ¹rahlim@yahoo.fr; ²saadisdz@gmail.com; ³l.hassaine@cder.dz.

^* Corresponding author, phone: +213665516070

Received: August 07, 2017 / Accepted: November 25, 2017 / Published: December 30, 2017

Abstract

This paper presents the modelling and simulation of a three-phase shunt active power filter (SAPF) using the direct power control (DPC) based on the Particle Swarm Optimization (PSO) algorithm for power quality improvement. In the DPC technique, the switches states of the inverter are selected from a table of switching based on the immediate errors between the active and reactive powers and their reference values. PSO algorithm is used in order to optimize the PI controller gains of the DC link voltage. This PI-PSO gives better results for robustness, harmonic minimization and reduces the overshoot and undershoot of PI controller. A MATLAB/SIMILINK simulation is provided to demonstrate the performance of the proposed approach.

Keywords

Shunt Active Power Filter; Direct power control; Particle Swarm Optimization

Introduction

Now in the power system the Power electronics converters are widely used. These equipment’s behave like nonlinear loads, generating harmonics and cause electromagnetic compatibility problems. Like the diode and thyristor rectifiers that absorb non-sinusoidal currents and inject of harmonic [1, 2, and 3]. This result in the reduction of power factor, reduces the efficiency and reduces the system performs.  Traditionally, the simplest method to eliminate current harmonics and to increase the power factor is the usage of passive LC. However, the use of passive filter has many disadvantages [4]. Recently, because of the rapid progress in modern power electronic technology, the previous works were oriented mostly on the active filters instead of passive filters.

The shunt active power filter (SAPF) is one of the most popular active filters. The shunt active power filter injects currents equal but opposite with the harmonic components, thus only the fundamental components flows in the point of common coupling (PCC). Various types of control of the three-phase shunts filters were presented in the literature, such as Voltage Oriented Control (VOC) [5] [6], the PQ theory, the synchronous reference current theory.

This paper describes the direct control of power controller based shunt active power filter for the harmonics and reactive power compensation due to the non-linear and unbalanced loads. The DPC strategy is based on the instantaneous active and reactive power comparators. The active power command is provided from a dc-bus voltage controller block, while the reactive power command is directly given from the outside of the controller. Errors between the commands and the estimated feedback power are input to the hysteresis comparators. Inner current control loops and PWM modulator are not required in DPC because the converter switching states are selected by a switching table based on the instantaneous errors between the commanded and estimated values of active and reactive powers [7].

 The optimization of PI regulator’s parameters is crucial [8] [9]. In this work, the active power is delivered from the outer proportional- integral controller this PI controller is formulated as an optimization problem.

The problem formulation assumes in this study the integral absolute time error of step as the objective function to determine the PI control parameters for getting a well performance under a given system. We propose an optimization method for SAPF in the aim to improve the compensation performances and reduce harmonic distortion through electrical lines distribution under all voltages conditions. These objectives are obtained by minimizing the fitness function.

In this work, we propose the use of the particle swarm optimization (PSO) method to search for the optimal parameters of a PI controller. DPC based on classical PI regulator and PSO algorithm are developed and a comparison study is presented. To show the performances, a numerical simulation is performed.

Material and method

Principle of the shunt active filter

The structure of the active filter consists essentially of two parts, a power and a control part (Figure 1).

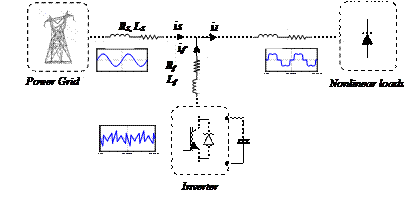
Figure 1. Principle of shunt active filter

The power part consists of an inverter, a coupling filter and a source of energy. The control part is used to control the switching of semiconductor elements forming the inverter from the power part.

Au through appropriate control strategies, it is possible to generate harmonic signals at the output of the inverter to offset those present on the power grid, such as, Eq. (1) [10].

(1)

Where: i_s – source current; i_l – load current; i_f – filter current.

Direct power control

The main idea of the direct power control (DPC) originally proposed by Ohnishi (1991) and further developed by Noguchi and Takahachi in 1998, is like the direct torque control (DTC) of induction machines. Instead of flux and torque, the active power (Ps) and reactive power (Qs) are selected as two instantaneous magnitudes to control [7]. The figure (3) shows the configuration of the direct power control for a three-phase inverter.

The estimated values of (Ps) and (Qs) in terms of the three phase line currents and voltages can be derived as Eq. (2-4) [7, 11].

	(2)
	(3)
	(4)

Where: S_s – source apparent power; i_s(abc) – three phase line currents; v_s(abc) – three phase line voltages.

Determination of sector

The phase of the power-source voltage vector is converted to the digitized signal. For this purpose, the working plane (α, β) is divided into 12 sectors (Figure 2).

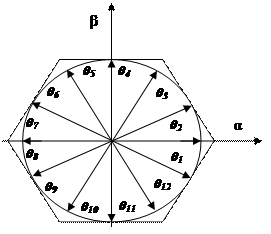
Figure 2. Plant (α, β) divided in 12 sectors

The sectors can be numerically determined by the following Eq. (5-6). [7].

(5)

Where: N= 1, 2, 3….12 is the number of the sector.

(6)

Where: θ – the line voltage vector position; V_α, V_β – the line voltage vector in plan (α, β).

Development of controllers

The references of reactive power (qref) and active power (pref) are compared with the estimated reactive (qs) and active (ps) values.

Errors between the commands and the estimated feedback power are input to the hysteresis comparators and digitized to the signals Sp and Sq. The output signal of the active power controller is defined in Eq. (7):

(7)

And similarly, for the reactive power controller as Eq. (8):

(8)

Where: hp – bandwidth hysteresis regulator of active power; hq – bandwidth hysteresis regulators of reactive power.

Switching table

For all sectors, the switching table proposed is represented in the Table 1.

Table 1. All sectors switching table

Sp	Sq	θ1	θ2	θ3	θ4	θ5	θ6	θ7	θ8	θ9	θ10	θ11	θ12
1	0	101	111	100	000	110	111	010	000	011	111	001	000
	1	111	111	000	000	111	111	000	000	111	111	000	000
0	0	101	100	100	110	110	010	010	011	011	001	001	101
	1	100	110	110	010	010	011	011	011	101	101	101	100

The synthesis of the switching table is based on the signs of derivatives of active and reactive power in each sector.

PI controller

The regulation of the continuous voltage of inverter is ensured by a regulator of PI type. The error between the voltage of the capacitor V_dc and the reference voltage V_dcref is used as an input to PI Controller and the output is the reference active power pref. The transfer function of the PI Controller is defined in Eq. (9):

(9)

This transfer function represents a second-order system.                                                            

Where: kp - is the proportional constant gain; ki - is the integral constant gain. These gains are tuned by using Particle Swarm Optimization (PSO).

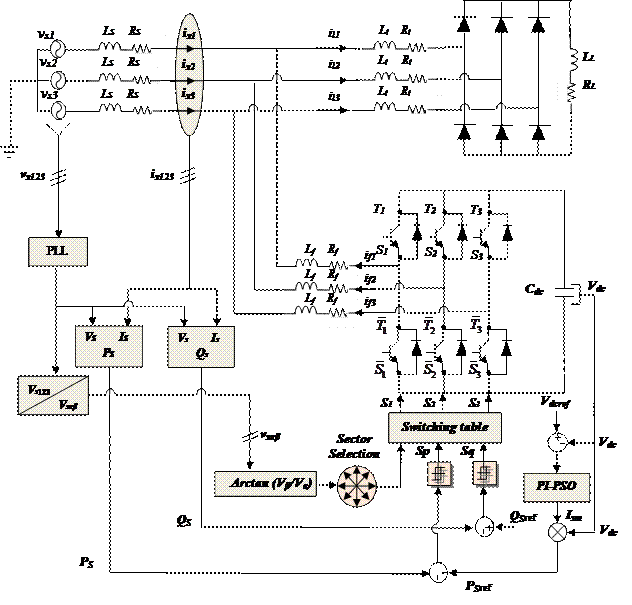
Figure 3. General structure of shunt active filter controlled by DPC with PI-PSO

Particle swarm optimization

The particle swarm optimization (PSO) algorithm was first described in 1995 by Kennedy and Eberhart [12, 13]. The technique has evolved greatly since then. PSO is a stochastic, population based evolutionary computer algorithm for problem solving. In a PSO system, a swarm of individuals (called particles) fly through the search space. Each particle represents a candidate solution to the optimization problem. The position of a particle is influenced by the best position visited by itself (i.e., its own experience) and the position of the best particle in its neighbourhood (i.e., the experience of neighbouring particles). When the neighbourhood of a particle is the entire swarm, the best position in the neighbourhood is referred to as the global best particle, and the resulting algorithm is referred to a global best PSO. When smaller neighbourhoods are used, the algorithm is generally referred to a local best PSO.

The performance of each particle (i.e., how close the particle is from the global optimum) is measured using a fitness function that varies depending on the optimization problem [12, 14]. The flow chart of the PSO algorithm is shown in Figure 4.

Figure 4. The flow chart of PSO algorithm

The personal best position of particle i is the best position visited by particle i so far. Let F denote the objective function.

Then the personal best of a particle at time step t is updated as Eq. (10):

(10)

Where: x_i – is the current position of the particle; y_i - is the personal best position of the particle.

For the global best model, the best particle is determined from the entire swarm by selecting the best personal position. If the position of the global best particle is denoted by the vector, then Eq. (11-12): 

	(11)
	(12)

Where:  – the neighbourhood best position of the particle; s – the size of the swarm; the velocity update step is specified for each dimension;  represents the j_th element of the velocity vector of the i_th particle.

Thus, the velocity of particle i is updated using the following Eq. (13):

(13)

After Eq. (13) we show the Eq. (14-15):

	(14)
	(15)

Where: ω – the inertia weight; , – the acceleration constants; ,  – the random coefficients distributed,   and .

The position of particle i, is then updated using the following Eq. (16):

(16)

This process is repeated until a specified number of iterations is exceeded, or velocity updates are close to zero. The quality of particles is measured using a fitness function which reflects the optimality of a particular solution.

The following steps summarize the basic PSO algorithm.

PSO Algorithm:

For each particle i=1, …, s do

Randomly initialize

Randomly initialize  (or just set to zero)

Set

end for

Repeat

For each particle i=1, …, s do

Evaluate the fitness of particle i,

Update using Eq. (11)

Update  using Eq. (13)

For each dimension j= 1, …, N_d  do

Apply velocity update using Eq. (14)

End loop

Apply position update using Eq. (16)

End loop

Until some convergence criteria is satisfied

Objective function formulation

In this study, the PSO algorithm is proposed to tune the PI parameters of voltage controller by minimizing the cost function. So that, the proportional (kp) and integral (ki) gains of PI controller is defined as the problem parameters that should be optimized. The proposed approach to find the optimal PI parameters is presented in Figure 5.

 Figure 5. Insertion of PSO approach with the PI controller

Thus, everyone of population is composed of the controller parameters kp and ki. Then, the optimization problem of PI controller is formulated as the minimization of the integral time absolute error ITAE and of the maximum overshoot.

Therefore, the objective function is defined as Eq. (17):

(17)

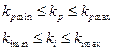
Where: n - is the total number of points for which the optimization is carried out; ts - is the time rang of simulation or simulation period.

Results and discussion

To prove the robustness and the performance of the proposed PI controller designed by PSO to the Direct Power Control Technique for Three-Phase Shunt Active Power Filter, the filtering system depicted in Figure 2 has been simulated using the SimPowerSystem with S-function of Matlab/Simulink installed on a computer system with Intel Core i5-4210 CPU, 1.70 GHz speed and 4GO of memory.

Parameters used in simulation are as follows (Table 2 and 3):

Table 2. Parameters of PSO algorithm

Parameter	Values
Swarm size	10
Number of iterations	100
r1	0.3
r2	0.95
c1	1.49
c2	1.49

Table 3. SAPF Parameters

Parameter	Values
Source voltage	220V
Supply frequency	50Hz
Source impedance Rs, Ls	3mΩ, 2.6 µH
Filter impedance Rf, Lf	20m Ω, 2.2mH
Line impedance Rl, Ll	10mΩ, 0.3mH
DC-link voltage reference Vdcref	700V
DC-link capacitor C	4500µF
Diode rectifier load RL, LL	20 Ω, 2mH

We have simulated the systems before and after the compensation, Figure 6 shows the system before harmonic compensation. The source voltages (vs), source current (is), active power (p) and reactive power (q) are depicted.

The supply current of phase A and its total harmonic distortion is represented in Figure 7.

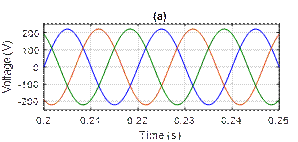
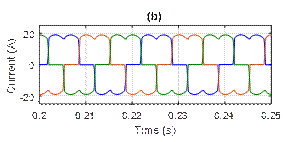
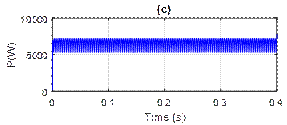
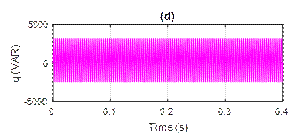
Figure 6.  Simulation results before harmonics compensation: (a) Source voltage, (b) Source current, (c) Active power, (d) Reactive power

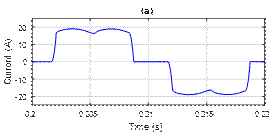
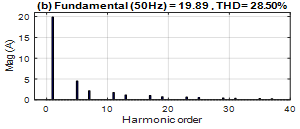
Figure 7. (a) Supply current before harmonics compensation, (b) Harmonic spectrum

The results show that the system is affected by the nonlinear load during the operation. Where, the Total Harmonic Distortion (THD) of the supply current is high and equals 28.50%.

Figure 8 and 10 shows the system after harmonic compensation for PI and PI-PSO controllers. The source current (is), source voltage (vs), filter current (if), DC bus voltage (Vdc), active power (p) and reactive power (q) are depicted. The sources current become perfectly sinusoidal compensated by the filter current at unity power factor. The reactive power is almost kept zero, which is compensated by the reactive current injected at the PCC via the SAPF.

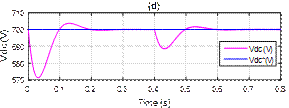
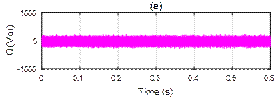
Figure 8. Simulation results with PI controller after harmonics compensation: (a) Source current, (b) Source voltage and source current of 1-phase, (c) Filter current, (d) DC-link voltage vdc, (e) Reactive power, (f) Active power

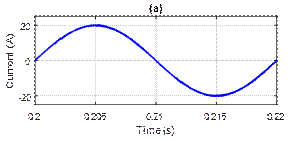
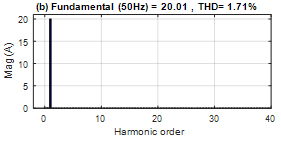
Figure 9. (a) Supply current after harmonics compensation using PI controller, (b) Its harmonic spectrum

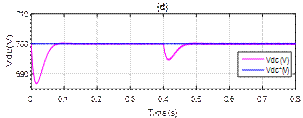
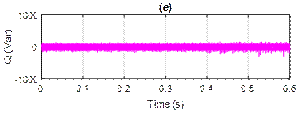
Figure 10. Simulation results with PI-PSO controller after harmonics compensation: (a) Source current, (b) Source voltage and source current of 1-phase, (c) Filter current, (d) DC-link voltage vdc, (e) Reactive power, (f) Active power

The dynamic behaviour under a step change of the load at t = 0.4s is presented in Figure. 8 and 10.

The source current presents significant variation in amplitude, although the form remains perfectly sinusoidal during change of load and injected current also is increased.

The active power was changed stepwise after varying the load which proves that the power consumed by the load is increased.

The reactive power continues to oscillate around zero.

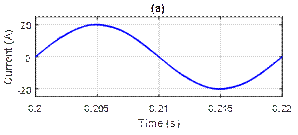
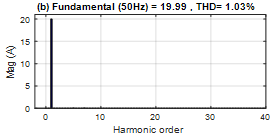
Figure 11. (a) Supply current after harmonics compensation using PI-PSO controller, (b) Its harmonic spectrum

The current source before and after application of the active filtering are represented on the figure 7, 9 and 11 the active filter decreases the total harmonic distortion (THD) from 28.50% to 1.71% with PI controller.

 However, with PI-PSO controller the THD is increased to 1.03% which proves the effectiveness of the proposed controller.

The error function evolution with iterations for PSO algorithm is presented in Figure 12.

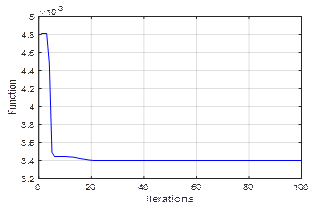
Figure 12. Error function evolution with iterations for PSO algorithm

The performance indices for SAPF considered are overshoot, % THD and ITAE and the values of the performance indices for switch-on response are listed in Table 4.

Table 4. Comparisons of SAPF indexes between used and unused PSO algorithm

Performance indices	Type of Controller
	Conv. PI	PI-PSO
Kp	0.2		0.512
Ki	10		20.92
Overshoot %	14.258		1.579
%THD	1.71		1.03
ITAE	0.1048		0.0151

The absence of an overshoot and undershoot in dc voltage response during load change with smallest amount of time and low source current THD, demonstrates the superiority of the PI-PSO controller compared to the PI controller.

Conclusions

This paper describes the design and simulation of a shunt active power filter (SAPF) using direct power control technique based PSO tuning.

The proposed control scheme is used to improve the performances of the DPC, in particular to achieve harmonics elimination, reactive power compensation, and dc voltage regulation.

To show the performances of the proposed methods, simulations were performed using Matlab-Simulink. The simulation results obtained in the various loading condition demonstrate the effectiveness and high robustness for both methods compared to classical DPC in terms of the current harmonic distortion, regulates the power factor and excellent transient response with minimal steady state error and lower overshoot.

References

1. Haddad M., Rahman S., Hamadi A., Al-Haddad K., New single phase multilevel reduced count devices to perform active power filter, Proceedings of the IEEE SoutheastCon, 2015, p. 1-6.

2. Zahzouh Z., Khochmane L., Haddouche A., Command of the novel multilevel active power filter by an algorithm through the P-Q developed, International Review on Modelling and Simulations (IREMOS), 2015, 8, p. 41-47.

3. Peng F. Z., Akagi H., Nabae A., A new approach to harmonic compensation in power systems: A combined system of shunt passive and series active filters, IEEE Transaction on Industry Application, 1990, 26, p. 983-990.

4. Chaoui A., Gaubert J., Karim F., Power quality improvement using DPC controlled three-phase shunt active filter, Electric Power Systems Research, 2010, 80, p. 657–666.

5. Kazmierkowski M. P., Malesani L., Current control techniques for three-phase voltage-source PWM converters. A survey, IEEE Transactions on Industrial Electronics, 1998, 45, p. 691–703.

6. Noguchi T., Tomiki H., Kondo S., Takahashi I., Direct power control of PWM converter without power-source voltage sensors, IEEE Transaction on Industry Application, 1998, 34, p. 473–479.

7. Bouzidi M., Bouafia S., Bouzidi A., Benaissa A., Barket S., Application of back stepping to the virtual flux direct power control of five-level three-phase shunt active power filter, International Journal of Power Electronics and Drive System (IJPEDS), 2014, 4, p. 173-191.

8. Berbaoui B., Benachaiba C., Rahli M., Tedjini H., An efficient algorithm to tuning PI-controller parameters for shunt active power filter using ant colony optimization, PRZEGLĄD ELEKTROTECHNICZNY (Electrical Review), 2011, 6, p. 140-145.

9. Gu J. J., Xu D. G., Active power filters technology and its development, Electric Machines and Control, 2003, 7, p. 126-132.

10. Antoniewicz K., Jasinski M., Kazmierkowsk M., Malinowski M., Model predictive control for 3-level 4-leg flying capacitor converter operating as shunt active power filter, IEEE Transactions on Industrial Electronics, 2016, 63, p. 5255–5262.

11. Chaoui A., Karim F., Gaubert J., Rambault L., DPC controlled three-phase active filter for power quality improvement, International Journal of Electrical Power & Energy Systems, 2008, 30, p. 476–485.

12. Kennedy J., Eberhart R. C., Particle swarm optimization, In Proceeding of IEEE International Conference on Neural Networks (Perth, Australia), 1995, p. 1942–1948.

13. Mazouze L., Zidi S. A., Saadi S., Benmessaoud T., Elaguab M., Hybrid swarm intelligence approach based PI regulator for VSC-HVDC optimal parameters, Journal of Electrical Engineering, 2014, 2, p. 362-370.

14. Mazouze L., Zidi S. A., Khatir M., Benmessaoud T., Saadi S., Particle swarm optimization based PI controller of VSC-HVDC system connected to a wind farm, International Journal of System Assurance Engineering and Management, 2016, 7, p. 239-246.

15. Saadi S., Elaguab M., Guessoum A., Bettayeb M., Optimizing UPFC parameters via two swarm algorithms synergy, In: Proceedings of the IEEE. Systems, signals and devices (SSD), 9th international multi-conference, Chemnitz, Germany, 2012.