Engineering, Environment
A new hybrid algorithm of particle swarm optimizer with grey wolves’ optimizer for solving optimal power flow problem
Aboubakr KHELIFI 1, Saliha CHETTIH 1and Bachir BENTOUATI 1*
1 LMSF Laboratory, Electrical Engineering Department, Laghouat 03000, Algeria,
E-mail(s): 1a.khelifi@lagh-univ.dz; 1s.chettih@lagh-univ.dz; 1*b.bentouati@lagh-univ.dz
* Corresponding author, +213 666 81 29 21
Received: June 17, 2018 / Accepted: June 17, 2018 / Published: June 30, 2018
Abstract
The current trend of study is to hybridize two and more algorithms to gain the best solution in the area of optimization problems. In this paper presents the recently developed hybrid optimization technique named PSO-GWO combines the framework of particle swarm optimization (PSO) with grey wolves optimization (GWO) to solve the optimal power flow (OPF) problem. OPF is formulated as a nonlinear optimization problem with conflicting objectives and subjected to both equality and inequality constraints. The performance of this technique is deliberated and evaluated on the standard IEEE 30-bus test system with a single objective and multi-objective cases such as fuel cost minimization, Active power loss reduction, Voltage profile improvement and Voltage stability enhancement, and is compared to approaches available in the literature. The hybrid PSO-GWO provides better results compared to the original PSO, GWO, and other techniques mentioned in the literature as shown in the simulation results.
Keywords
Optimal power flow; Voltage stability; Active power loss; Emission; Constraints; Hybrid PSO-GWO.
Introduction
The Optimal Power Flow (OPF) is a significant appliance for planning and operation studies in the power system operator. OPF is a widely non-linear and non-convex optimization problem, and this is more difficulty in practical applications in the large number's presence of discrete variables. The goal of OPF is to provide the optimal settings of the power system by improving objective function while meeting the equality and inequality constraints [1], then this problem has been addressed by several researchers. The objective functions, such as the minimization of total fuel cost, improvement of voltage stability index and reduction of real power loss are considered individually in the literature for this study.
The problem of power flow is one of the fundamental problems in which the load and the powers of the generator are given or corrected. The OPF has a long history in its development, and it was primarily introduced by Carpentier in 1962, and the next investigations on OPF in [2]. However, it took a long time to turn into an effective technique that could be applied in daily use. The actual interest for OPF is focused on its capability to solve for the optimal solution that has considered the security of the system. The optimal power flow has been applied to regulate the active power outputs and voltages of the generator, transformer tap settings, shunt reactors/capacitors and other controllable variables to minimize the generator fuel cost, network active power loss, voltage stability index, while keeping all the load bus voltages, generator reactive power outputs, network power flows, and all other state variables in the power system within their secure and operational bounds. In its most common problem formulation, the OPF is a non-convex, static, large-scale optimization problem with both continuous and discrete control variables [3]. Even in the absence of non-convex generator operating cost functions, prohibited operating zones (POZs) of generating units, and discrete control variables, the OPF problem is a non-convex because of the existence of the non-linear alternating current power flow equality constraints. The existence of discrete control variables, such as transformer tap positions, switchable shunt devices, phase shifters, further complicates the formulation and solution of the problem.
Different conventional optimization methods have been used to solve the OPF problem. These involve Newton methods [4], linear programming [5], and quadratic programming [6]. A comprehensive survey of different conventional optimization techniques used to solve OPF problems was presented. Nevertheless, in practice, conventional techniques suffer from some weakness. Some of its shortcomings through other things are: First, they do not assure to find the global optimum, second, conventional techniques involve complex computations with a long time, and they do not suitable for discrete variables [7].
During the last little decades, a lot of powerful meta-heuristics were developed. Several of them have been implemented to the OPF problem with very successfully. various of the modern implementations of meta-heuristics for the OPF problem are: Black Hole (BH) [8], League Championship Algorithm (LCA) [9], Gravitational Search Algorithm (GSA)[10], Artificial Bee Colony (ABC)[11], Group Search Optimization (GSO)[12], Imperialist Competitive Algorithm (ICA) [13], Differential Search Algorithm (DSA) [14], Teaching Learning Based Optimization (TLBO)[15], and Krill Herd Algorithm (KHA) [16], adaptive clonal selection algorithm(ACSA) [17] .Though, because of changing objectives while solving OPF problems, no algorithm is the greatest one to solve all the OPF problems. Consequently, there is still a need for a novel algorithm, which can effectively solve the most of OPF problems.
Particle Swarm Optimization (PSO) has an uncomplicated concept, simple to carry out, Relative effectiveness to control parameters and computational adequacy[18] Although it has many advantages, it obtain restricted in the local minimum, When dealing with severely constrained problems because of limited local/global search abilities [19, 20]. Gray Wolf Optimizer (GWO) is a powerful evolutionary algorithm newly developed by Mirjalili [20] it has the capability to converge to the superior quality near-optimal solution and has preferable convergence properties than other dominant techniques. In addition, GWO has a perfect balance between exploration and exploitation that result in avoidance high of the local optima.
In this article, we introduce a new hybrid algorithm, named a PSO-GWO which is constructed on incorporating PSO with GWO algorithms. The effectiveness of this technique to the OPF problem with non-smooth cost functions like as fuel cost with prohibited zones, piecewise quadratic cost function, fuel cost with valve-point effects is tested and analyzed on the standard IEEE 30-bus test systems With various objective functions and is Compared to the techniques mentioned in the literature. Investigational results on the OPF problem show that the modern hybrid algorithm has preferable effectiveness in both convergence and global excellent, compared with original PSO, GWO and other algorithms mentioned in the literature. We confirm that the suggested method has perfect efficiency and capability to get a solution of OPF problem. This suggested technique can optimize the number of various objectives and can be useful for system operators in choosing a wise decision in implementing the system performance.
Material and method
Optimal Power Flow formulation
The OPF is a power flow problem that provides the optimal settings of the control variables for specific settings of the load by means of reducing a predefined objective function such as the cost of real power generation or transmission losses. OPF takes into account the operating limits of the system and it can be mathematically formulated as a nonlinear constrained optimization problem as follows, Eq. (1):
Minimize: J (𝑥, 𝑢) (1)
![]()
Subject to: ![]()
Where: J (x, u) - objective function; h (x, u) - set of equality constraints; g(x, u) - set of inequality constraints; U - the vector of control variables; X - the vector of state variables; the control variables u and the state variables x of the OPF problem are explained in (2) and (3), respectively.
Control variables:
These are the set of variables that can be regulated to satisfy the load flow equations [21]. The set of control variables in the mathematical formulation of the OPF problem are:
PG: is the 𝑖-th active power bus generator (except swing generator).
VG: is the voltage magnitude at 𝑖-th PV bus (generator bus).
T: is the transformer tap setting.
QC: is the shunt VAR compensation.
The control variables U can be formulated as Eq. (2):
![]() (2)
(2)
Where: NC, NT and NG are the number of VAR compensator, the number of regulating transformers and the number of generators respectively.
State variables:
These are the set of variables that report any unique state of the system [21]. The set of state variables for mathematically formulated the OPF problem as follow:
PG1: is the generator active power at slack (or swing) bus.
VL: is the bus voltage of 𝑝-th load bus (PQ bus).
QG: reactive power generation of all generator units.
SL: transmission line loading (or line flow)
The state variables X can be formulated as Eq. (3):
![]() (3)
(3)
Where: NL, and nl are the number of load buses and the number of transmission lines, respectively.
Constraints:
The OPF constraints can be classified into equality and inequality constraints, as explained in the next sections.
- Equality constraints
The equality constraints that express the typical nonlinear power flow equations that control the power system, presented as follows.
a) Real power constraints, Eq. (4):
![]() (4)
(4)
b) Reactive power constraints, Eq. (5):
![]() (5)
(5)
Where: NB is the
number of buses, ![]() and
and![]() are active and
reactive load demands, respectively,
are active and
reactive load demands, respectively, ![]() is the difference in voltage angles
between bus 𝑖 and
bus 𝑗
is the difference in voltage angles
between bus 𝑖 and
bus 𝑗 ![]() is the transfer
conductance and
is the transfer
conductance and ![]() is
the susceptance between bus 𝑖 and bus 𝑗,
respectively.
is
the susceptance between bus 𝑖 and bus 𝑗,
respectively.
- Inequality constraints:
The Inequality constraints that reflect operational of the system and the system's physical limits presented as follows.
1. Generator constraints. For all generators comprising the slack: voltage, active and reactive outputs shall be limited by their minimum and maximum limits as follows, Eq. (6-8):
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
2. Transformer constraints. Transformer tap settings must be limited to their specified minimum and maximum limits as follows, Eq. (9):
![]() (9)
(9)
Shunt VAR compensator constraints. Shunt VAR compensator have to be limited by their lower and upper limits as follows, Eq. (10):
![]() (10)
(10)
Security constraints:
These comprise the constraints of voltage magnitude at load buses and transmission line loadings. The Voltage of each load bus has to be limited within its minimum and maximum operating limits. Line flow through each transmission line must be limited by its capacity limits. These constraints can be expressed as given follows, Eq. (11-12):
![]() (11)
(11)
![]() (12)
(12)
Where: ![]() and
and ![]() - represents lowest
and the upper load voltage of i-th unit,
- represents lowest
and the upper load voltage of i-th unit,![]() - represents apparent power flow of i-th
branch
- represents apparent power flow of i-th
branch ![]() - represents
maximum apparent power flow limit of i-th branch.
- represents
maximum apparent power flow limit of i-th branch.
Particle swarm optimization (PSO):
Particle swarm optimization, inspired by societal the conduct of birds is an optimization technique based on swarm intelligence that suggested a population-based research process by taking particles and moving them around in the search space for be given the best solution for the problem. In PSO, particles change position in a multi-dimensional search space, any particle adjusts its location pursuant to its own experiment and the experiment of neighbouring particles, and take advantage of the best position encountered by itself and its neighbours. The direction of the swarm of a particle is determined by all the neighbouring particles of the particle and experiment of its history [22]. PSO is a non-deterministic, stochastic optimization method and supplies a population-based search operation for global optimization, Have the main advantage of easy to achieve and few parameters to regulate. PSO involves two expressions A and B. Position and speed are updated over the course of iteration from these follows Eq. (13-15):
![]() (13)
(13)
![]() i=1,2….NP
j=1,2….NG (14)
i=1,2….NP
j=1,2….NG (14)
![]() (15)
(15)
Where: vijt+1, vijt is the speed of j-th member of i-th particle at iteration number, r1 and r2 are two random values within [0, 1].
Grey wolf optimization (GWO)
Mirjalili et al are the first to propose a new algorithm called are Grey Wolf Optimization [23], The technique was inspired by the popular conduct and hunting mechanism of grey wolves in nature. In a group, the grey wolves follow so strong social leadership hierarchy. The group leaders are male and female, named alpha (α). The second level of grey wolves, which are subaltern wolves that assist leaders, are named beta (β). The deltas (δ) are the grey wolves' third level that must submit to alphas and betas but controls the omega. The downgrade of the grey wolf is omega (ω), which must capitulate to all other wolves that govern. The GWO technique is presented in mathematical models as next [24].
Social hierarchy
In the mathematical pattern of the social hierarchy of grey wolves, alpha (α) is considered the most suitable solution. As a result, the second preferable solution is called beta (β) and the third preferable solution is called delta (δ) respectively. The remaining candidate solutions are taken as omega (ω). In the GWO, the optimal (shooting) alpha, beta, and delta are guided. The omega wolves must come behind these wolves [24].
Encircling prey
The grey wolves surround victim through the hunt. The encircling conduct can be modelled mathematically as follows, Eq. (16-17):
![]() (16)
(16)
![]() (17)
(17)
Where: ![]() - shows the existing
iteration,
- shows the existing
iteration, ![]() and
and
![]() are
coefficient vectors,
are
coefficient vectors, ![]() is the position vector of the victim and
is the position vector of the victim and
![]() shows the
position vector of a grey wolf. The vectors
shows the
position vector of a grey wolf. The vectors ![]() and
and ![]() are calculated as follows, Eq. (18-19):
are calculated as follows, Eq. (18-19):
![]() (18)
(18)
![]() (19)
(19)
Where: elements of 'l' are linearly diminished from 2 to 0 through the course of iterations and r1, r2 are arbitrary vectors in the cavity [0,1].
Hunting
Hunting is generally guided by alpha, beta and delta, which have a better understanding of the potential location of the victim. The other search agents have to update their positions based on the preferable search position of agent. The position of their agent update can be expressed as follows Eq. (20-22) [25]:
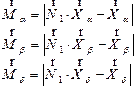 (20)
(20)
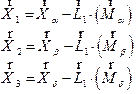 (21)
(21)
![]() (22)
(22)
Search for prey and attacking prey
The 'L' is an arbitrary value in the interval [-2a, 2a].When | L | <1, the wolves are forced to offensive the victim. Offensive the victim is the exploitation capability and searching for a victim is the exploration capability. The random values of 'L' are employed to force the search agent to move far from the victim. When | L | > 1, grey wolves are forced to move far from the victim.
Hybrid PSO-GWO
Whoever the technique is used for optimization, it has advantages and disadvantages. Exams were suggested for enhancement to achieve the best possible technique. Hybridization techniques can help to find enhancement in order to the advantages and disadvantages of each technique are compensated. Presently, the hybrid meta-heuristics have become more deliberative in order to the best results for some optimization problems have been received with hybrid methods. In this article, we have select two new meta-heuristics (PSO and GWO) to solve the OPF problem, but like all techniques, PSO and GWO have advantages and disadvantages. So as to combine the characteristics of the two techniques to draw their benefits and have the preferable results, we hybridized them as appear in Figure 1.

Figure 1. Flowchart of the hybrid GWO-PSO algorithm
The PSO-GWO algorithm has been using to solve the OPF problem for exam system and for many cases with various objective functions. The considered power systems networks are the IEEE 30-bus test system network. The advanced software program is written in MATLAB computing environment and used on a 2.20 GHz i7 personal computer. In our study, the PSO-GWO population size or a number of stars is selection to be 50.
IEEE 30-bus test system
In order to illustrate the performance of the proposed PSO-GWO method, it has been examined first on the standard IEEE 30-bus test system. The standard IEEE 30-bus system selection in this paper has the next characteristics [26]: 6-generators at buses 1, 2, 5, 8, 11 and 13, 4-transformers with off-nominal tap ratio at lines 11, 12, 15 and 36, 9- shunt VAR compensation buses at buses 10, 12, 15, 17, 20, 21, 23, 24 and 29.
In addition, line data, bus data, generator data, and lower and upper restriction for control variables are presented in [27].
For this exam system, Six various cases have been studied with various objectives and all the obtained results are outlined in Tables 1, 4 and 7. The first column of this table appears the optimal control settings found here:
- PG1Through PG6 and VG1 through VG6 represent the powers and the voltages of generator 1 through generator 6.
- T11, T12, T15 and T36 are the tap settings of transforms involved between lines 11, 12, 15 and 36.
- QC10, QC12, QC15, QC17, QC20, QC21, QC23, QC24 and QC29 represent the shunt VAR compensations connected to buses 10, 12,15, 17, 20, 21, 23, 24 and 29.
Moreover, fuel cost ($/h), active power losses (MW),
voltage deviation and ![]() represent
the total fuel cost of the system, the total active transmission losses, the
deviation of load voltages from 1and the index of stability, respectively.
More description of these results will be presented in the next sections.
represent
the total fuel cost of the system, the total active transmission losses, the
deviation of load voltages from 1and the index of stability, respectively.
More description of these results will be presented in the next sections.
Case 1: Minimization of generation fuel cost
The first case studied in this article is the basic case of minimizing the cost generation fuel expressed by a quadratic function. Therefore, the objective function of this case is Eq. (23):
![]() (23)
(23)
Where: fi - is the fuel cost of the ith generator. Usually, the OPF generation fuel cost curve is formulated by a quadratic function.
Hence, fi can be formulated as follows Eq. (24):
![]() (24)
(24)
Where: ai, bi, ci - are the element, the linear and the quadratic cost coefficients of the ith generator, respectively. The values of these coefficients are presented in [27].
Figure 2 appears the trend of total fuel cost over iterations. It seems that the proposed technique has good convergence characteristics. The optimal settings of control variables are presented in Table 1. The total fuel cost obtained by the suggested PSO-GWO technique is (799.1079 $/h). Compared to the original PSO, GWO the total fuel cost is significantly decreased.
Using the identical conditions (limits of control variables, initial conditions, and system data), the results obtained in Case 1 apply the PSO-GWO technique are compared to other methods described in the literature as appears in Table 2. There is some proof, that the suggested technique outperforms several methods used to solve the OPF problem by decreasing of generation fuel cost. For instance, the results obtained by the PSO-GWO are better than the ones obtained the GWO and PSO methods.
Case 2: Minimization of fuel cost and voltage deviation
Bus voltage is one of the most significant and considerable security and service quality indices [27]. Reducing only the total cost in the OPF problem as in Case 1 may result in a suitable Solution, but voltage profile may not be reasonable. Consequently, this case purposes at minimizing fuel cost with a improve voltage profile by considering a dual objective function.
The voltage profile is optimized by reducing the load bus voltage deviation (VD) from 1.0 p.u, the objective function, in this case, can be formulated as follows Eq. (25):
![]() (25)
(25)
Where: w - is an appropriate weighting factor, to be chosen by the user to accord a weight to each of the two expressions of the objective function. In this case, w is selection as 100.
![]() and
and ![]() are
presented as follows Eq. (26-27):
are
presented as follows Eq. (26-27):
![]() (26)
(26)
![]() (27)
(27)
Results and discussion
The PSO-GWO technique has been utilized to search for the optimal solution of the problem. The variations in the fuel cost and voltage deviation through the iterations are outlined in Figure 3a and Figure 3b.
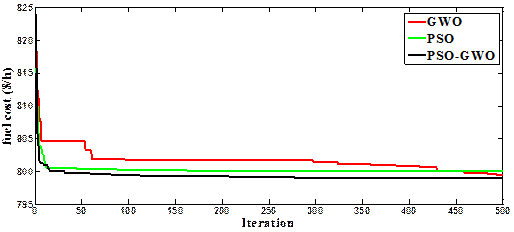
Figure 2. Convergent curves of Case 1
The optimal settings of the control variables are presented in Table 1. Apply PSO-GWO the fuel cost and the voltage deviation yielded are (803.5881$/h) and (0.1044 p.u.), respectively. The voltage profile obtained by PSO-GWO is compared with other algorithms as appears in Table 2. It is clear that the voltage profile is the least among all other comparable methods. It is decreased from 1.6899 p.u. in the case 1 to 0.1044 p.u. in case 2, Hence, in case 2, the fuel cost is slightly augmented by 0.55% compared to case 1.
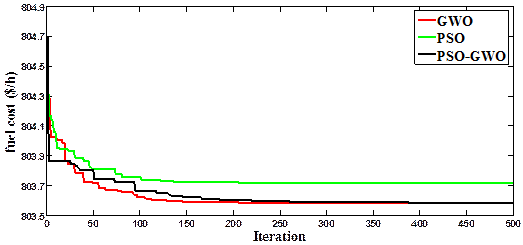
Figure 3a. Convergent curves of Case 2
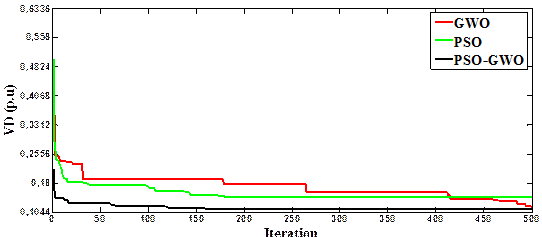
Figure 3b. Convergent curves of Case 2
CASE 3: Minimization of fuel cost considering valve point effect
So as to have a realistic and greater effective modeling of generator cost functions, the valve point–effect must be considered. The generating units with multi-valve steam turbines display a major variation in the fuel-cost functions and output a ripple-like effect [30]. So as to considered the valve-point effect of generating units, a modeled as a sinusoidal term is added to the cost function. Thus, the objective function can be formulated as follow Table 1 and Table 2:
Table 1. Optimal settings of the control variables for case1 to case 3.
|
Control variable |
Case 1 |
Case 2 |
Case 3 |
||||||||
|
PSO-GWO |
GWO |
PSO |
PSO-GWO |
GWO |
PSO |
PSO-GWO |
GWO |
PSO |
|||
|
PG1 (MW) |
176.57 |
176.66 |
177.84 |
177.52 |
176.09 |
178.16 |
200.17 |
200.08 |
200.00 |
||
|
PG2 (MW) |
48.81 |
47.83 |
49.06 |
49.26 |
48.92 |
49.11 |
43.14 |
41.86 |
43.53 |
||
|
PG5 (MW) |
21.61 |
21.19 |
21.48 |
21.77 |
21.59 |
21.64 |
18.32 |
18.49 |
18.63 |
||
|
PG8 (MW) |
21.02 |
20.25 |
22.09 |
22.74 |
22.39 |
22.44 |
10.08 |
11.28 |
10.00 |
||
|
PG11 (MW) |
11.78 |
12.91 |
10 |
10 |
12.21 |
10.04 |
10.00 |
10.01 |
10.00 |
||
|
PG13 (MW) |
12.21 |
13.21 |
12 |
12 |
12 |
12 |
12.00 |
12.01 |
12.00 |
||
|
V1(p.u) |
1.1 |
1.1 |
1.1 |
1.05 |
1.04 |
1.06 |
1.10 |
1.10 |
1.10 |
||
|
V2(p.u) |
1.09 |
1.09 |
1.1 |
1.03 |
1.02 |
1.04 |
1.08 |
1.09 |
1.10 |
||
|
V5(p.u) |
1.06 |
1.06 |
1.1 |
1.01 |
1.01 |
1.01 |
1.06 |
1.06 |
1.08 |
||
|
V8(p.u) |
1.07 |
1.07 |
1.1 |
1.00 |
1.01 |
1.00 |
1.06 |
1.07 |
1.10 |
||
|
V11(p.u) |
1.1 |
1.1 |
1.1 |
1.1 |
0.98 |
1.1 |
1.10 |
1.09 |
1.10 |
||
|
V13(p.u) |
1.1 |
1.1 |
1.1 |
0.97 |
1.03 |
0.96 |
1.10 |
1.10 |
1.10 |
||
|
Qc10(Mvar) |
1.80 |
0.38 |
0 |
0 |
0 |
0 |
5.00 |
0.18 |
0 |
||
|
Qc12(Mvar) |
2 |
0.12 |
0 |
1.35 |
2.24e-06 |
5 |
0.25 |
0.23 |
5.00 |
||
|
Qc15(Mvar) |
5 |
1.57 |
0 |
5 |
5 |
5 |
3.92 |
0.12 |
5.00 |
||
|
Qc17(Mvar) |
5 |
0.09 |
0 |
0 |
5 |
5 |
3.53 |
0.22 |
0 |
||
|
Qc20(Mvar) |
0.01 |
2.47 |
5 |
5 |
5 |
5 |
0.59 |
3.43 |
0 |
||
|
Qc21(Mvar) |
4.87 |
1.49 |
5 |
5 |
5 |
5 |
5.00 |
2.68 |
5.00 |
||
|
Qc23(Mvar) |
3.08 |
1.58 |
5 |
5 |
5 |
5 |
0.02 |
0.07 |
3.66 |
||
|
Qc24(Mvar) |
5 |
1.79 |
5 |
4.93 |
5 |
5 |
5.00 |
1.49 |
5.00 |
||
|
Qc29(Mvar) |
0.46 |
3.22 |
0 |
2.64 |
5 |
5 |
3.81 |
1.61 |
5.00 |
||
|
T6–9 |
1.04 |
1.04 |
1.1 |
1.1 |
0.99 |
0.96 |
1.02 |
1.08 |
0.99 |
||
|
T6–10 |
0.90 |
0.92 |
0.9 |
0.9 |
0.9 |
1.1 |
0.93 |
0.93 |
1.10 |
||
|
T4–12 |
1.07 |
1.02 |
1.02 |
0.92 |
1.02 |
0.9 |
1.01 |
1.06 |
1.10 |
||
|
T28–27 |
0.96 |
0.99 |
0.99 |
0.97 |
0.98 |
0.98 |
0.99 |
0.99 |
1.10 |
||
|
Fuel cost ($/h) |
799.1079 |
799.5063 |
800.4361 |
803.5881 |
803.5802 |
803.7326 |
829.8394 |
830.4784 |
831.6223 |
||
|
VD |
1.6899 |
1.3010 |
1.6857 |
0.1044 |
0.1151 |
0.1464 |
1.5136 |
0.9963 |
1.0404 |
||
|
|
0.1283 |
0.1338 |
0.1294 |
0.1487 |
0.1491 |
0.1490 |
0.1321 |
0.1362 |
0.1453 |
||
|
Emission (ton/h) |
0.3646 |
0.3642 |
0.3687 |
0.3677 |
0.3631 |
0.3695 |
0.4433 |
0.4426 |
0.4425 |
||
|
|
8.5944 |
8.6613 |
9.0431 |
9.8890 |
9.8007 |
9.9780 |
10.3089 |
10.3455 |
10.7552 |
||
Table 2. Comparison of the results obtained for Case 1to Case 3.
|
Case 1 |
Case 2 |
Case 3 |
|||
|
Algorithms |
Fuel cost ($/h) |
Algorithms |
VD (pu) |
Algorithms |
Fuel cost ($/h) |
|
PSO-GWO |
799.1079 |
PSO-GWO |
0.1044 |
PSO-GWO |
829.8394 |
|
GWO |
799.5063 |
GWO |
0.1151 |
GWO |
830.4784 |
|
PSO |
800.4361 |
PSO |
0.1464 |
PSO |
831.6223 |
|
MGBICA [31] |
801.1409 |
BHBO [8] |
0.1262 |
ICBO[36] |
830.4531 |
|
ABC [32] |
800.660 |
DE [34] |
0.1357 |
BSA[21] |
830.7779 |
|
HSFLA-SA[33] |
801.79 |
IEM [35] |
0.1270 |
|
|
![]() (28)
(28)
Where: ![]() and
and ![]() are the
coefficients that show the valve-point loading effect.
are the
coefficients that show the valve-point loading effect.
In this case to arrive at a rise in cost than in case 1 with a conclusive value being 829.8394$/h, obtained by PSO-GWO. The optimal control variables obtained are shown in Table 1 output outcome of a method used in our study are better than most of the results revealed in past literature on the problem of OPF that is presented in table 2.
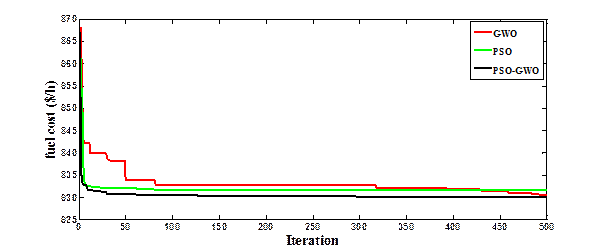
Figure 4. Convergent curves of Case 3
Case 4: Minimization of fuel cost and enhancement of voltage stability
The prediction of voltage instability is a problem of paramount
significance in power systems. In [28] Kessel and Glavitch
have developed a voltage stability index named![]() which is defined build on local
indicators
which is defined build on local
indicators ![]() and
it is presented by Eq. (29):
and
it is presented by Eq. (29):
![]() ,
, ![]() (29)
(29)
Where: ![]() is the local
indicator of bus j and it is given as follows Eq. (30)
is the local
indicator of bus j and it is given as follows Eq. (30)
![]()
![]() (30)
(30)
Where: H - matrix is produced by the partial inversion of Ybus. More specifics can be given in [28].
The indicator![]() varies between 0 and 1 where the lower the indicator, the more the system
stable. Thus, enhancing voltage stability can be obtained by the minimization
of
varies between 0 and 1 where the lower the indicator, the more the system
stable. Thus, enhancing voltage stability can be obtained by the minimization
of![]() the
complete system [29]. Hence, the objective function can be formulated as Eq.
(31):
the
complete system [29]. Hence, the objective function can be formulated as Eq.
(31):
![]() (31)
(31)
Where: ![]() is
a weighting factor chosen as 100 in this work. The results of the optimization
study are presented in Table 3 while the direction of convergence appears in
Figure 5a and 5b. It seems that the Lmax has
been decreased from 0.1283 to 0.1251compared with CASE 1,
is
a weighting factor chosen as 100 in this work. The results of the optimization
study are presented in Table 3 while the direction of convergence appears in
Figure 5a and 5b. It seems that the Lmax has
been decreased from 0.1283 to 0.1251compared with CASE 1,
Hence the results obtained are compared with other algorithms as given in Table 4.
Table 3. Optimal settings of the control variables for case 4 to case 6.
|
Control variable |
Case 4 |
Case 5 |
Case 6 |
|||||||||||
|
PSO-GWO |
GWO |
PSO |
PSO-GWO |
GWO |
PSO |
PSO-GWO |
GWO |
PSO |
||||||
|
PG1 (MW) |
177.13 |
178.06 |
177.9656 |
113.11 |
112.85 |
111.84 |
51.39 |
51.55 |
51.37 |
|||||
|
PG2 (MW) |
49.22 |
49.64 |
49.1534 |
59.11 |
58.98 |
58.40 |
79.93 |
79.91 |
80.00 |
|||||
|
PG5 (MW) |
21.99 |
21.99 |
21.3946 |
27.48 |
27.61 |
27.35 |
50.00 |
49.96 |
50.00 |
|||||
|
PG8 (MW) |
18.60 |
19.01 |
21.9131 |
35.00 |
35.00 |
35.00 |
35.00 |
34.94 |
35.00 |
|||||
|
PG11 (MW) |
12.28 |
11.51 |
10.0000 |
26.60 |
27.87 |
30.00 |
29.99 |
30.00 |
30.00 |
|||||
|
PG13 (MW) |
12.98 |
12.14 |
12.0000 |
27.19 |
26.29 |
26.05 |
40.00 |
39.95 |
40.00 |
|||||
|
V1(p.u) |
1.10 |
1.10 |
1.1000 |
1.10 |
1.10 |
1.10 |
1.10 |
1.10 |
1.10 |
|||||
|
V2(p.u) |
1.09 |
1.09 |
1.1000 |
1.09 |
1.09 |
1.10 |
1.10 |
1.10 |
1.10 |
|||||
|
V5(p.u) |
1.07 |
1.07 |
1.0744 |
1.07 |
1.07 |
1.08 |
1.08 |
1.08 |
1.10 |
|||||
|
V8(p.u) |
1.07 |
1.08 |
1.0852 |
1.08 |
1.08 |
1.10 |
1.09 |
1.09 |
1.10 |
|||||
|
V11(p.u) |
1.10 |
1.10 |
1.0624 |
1.10 |
1.10 |
1.10 |
1.10 |
1.10 |
1.10 |
|||||
|
V13(p.u) |
1.10 |
1.10 |
1.1000 |
1.10 |
1.10 |
1.10 |
1.10 |
1.10 |
1.10 |
|||||
|
Qc10(Mvar) |
5.00 |
1.81 |
0 |
2.89 |
2.24 |
5.00 |
0.01 |
3.44 |
5.00 |
|||||
|
Qc12(Mvar) |
0.05 |
0.30 |
5.0000 |
0.96 |
3.62 |
0 |
0.47 |
0.85 |
5.00 |
|||||
|
Qc15(Mvar) |
3.04 |
0.39 |
0 |
5.00 |
1.22 |
0 |
2.71 |
2.78 |
5.00 |
|||||
|
Qc17(Mvar) |
0.02 |
1.73 |
5.0000 |
4.72 |
0.53 |
5.00 |
4.58 |
3.83 |
0 |
|||||
|
Qc20(Mbar) |
5.00 |
0.10 |
5.0000 |
3.91 |
0.00 |
0 |
5.00 |
1.07 |
0 |
|||||
|
Qc21(Mvar) |
0.36 |
4.87 |
0 |
0.27 |
1.33 |
5.00 |
0.50 |
3.70 |
5.00 |
|||||
|
Qc23(Mvar) |
0.51 |
0.17 |
5.0000 |
1.82 |
1.74 |
0 |
4.27 |
3.86 |
0 |
|||||
|
Qc24(Mvar) |
0.62 |
0.55 |
5.0000 |
5.00 |
0.03 |
0 |
5.00 |
1.02 |
5.00 |
|||||
|
Qc29(Mvar) |
0.84 |
0.24 |
0 |
1.14 |
0.02 |
2.21 |
0.03 |
1.80 |
2.21 |
|||||
|
T6–9 |
0.99 |
0.98 |
0.9000 |
1.04 |
0.97 |
0.97 |
1.04 |
1.08 |
1.10 |
|||||
|
T6–10 |
0.91 |
0.93 |
1.1000 |
0.92 |
1.02 |
1.10 |
0.92 |
0.90 |
0.90 |
|||||
|
T4–12 |
0.99 |
0.98 |
1.0132 |
1.01 |
1.03 |
1.10 |
1.01 |
1.00 |
1.01 |
|||||
|
T28–27 |
0.94 |
0.94 |
0.9426 |
0.99 |
0.98 |
1.01 |
0.97 |
0.99 |
0.99 |
|||||
|
Fuel cost ($/h) |
799.7188 |
799.9043 |
800.3247 |
834.9486 |
835.9200 |
838.1687 |
966.9805 |
966.5853 |
967.3598 |
|||||
|
VD |
1.8169 |
1.7976 |
1.7615 |
1.6909 |
1.3259 |
1.2613 |
1.8087 |
1.6767 |
1.8015 |
|||||
|
|
0.1251 |
0.1250 |
0.1255 |
0.1303 |
0.1327 |
0.1343 |
0.1281 |
0.1302 |
0.1282 |
|||||
|
Emission (ton/h) |
0.3659 |
0.3690 |
0.3692 |
0.2426 |
0.2422 |
0.2406 |
0.2072 |
0.2072 |
0.2072 |
|||||
|
|
8.7897 |
8.9339 |
9.0267 |
5.0851 |
5.1929 |
5.2424 |
2.8946 |
2.9100 |
2.9732 |
|||||
Table 4. Comparison of the results obtained for Case 4 to Case 6.
|
Case 4 |
Case 5 |
Case 6 |
|||
|
Algorithms |
|
Algorithms |
Emission(ton/h) |
Algorithms |
Ploss (MW) |
|
PSO-GWO |
0.1251 |
PSO-GWO |
0.2426 |
PSO-GWO |
2.8946 |
|
GWO |
0.1250 |
GWO |
0.2422 |
GWO |
2.9100 |
|
PSO |
0.1255 |
PSO |
0.2406 |
PSO |
2.9732 |
|
ABC [32] |
0.1379 |
MOGWO [40] |
0.245126 |
MSA[39] |
3.1005 |
|
ARCBBO[37] |
0.1369 |
NSGA-II[40] |
0.3214 |
ABC[32] |
3.1078 |
|
Gbest-ABC [38] |
0.1370 |
|
|
ARCBBO[37] |
3.1009 |
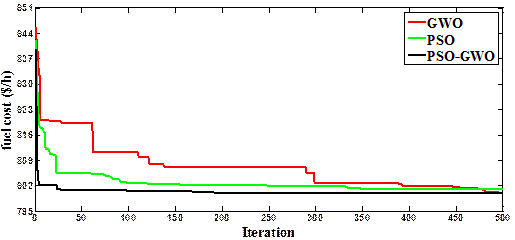
Figure 5a. Convergent curves of Case 4
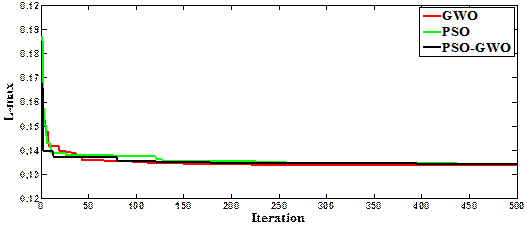
Figure 5b. Convergent curves of Case 4
CASE 5: Minimization of fuel cost and emission
Electrical power generation from conventional sources of energy emits hazardous gases into the environment. The quantity of sulfur oxides (SOx), nitrogen oxides (NOx) emission in tons per hr (t/h) is higher with the rise in generated power (in p.u. MW) next to the relationship presented in Eq. (32).
![]() (32)
(32)
Where: αi, βi, Υi, ωi
and μi are all emission coefficients provided in [21]. The
objective function for this case is assumed by Eq. (33):
![]() (33)
(33)
The weight factors are selected as ![]() = 100 in this case.
= 100 in this case.
The results yielded after optimization applied the PSO-GWO technique are presented in Table 3 and the trend of optimization is shown in Figure 6. The results appear that the emission has been decreased from (0.3646 ton/h) to (0.2426 ton/h), Thus, the total fuel cost has augmented from (799.1079$/h) to (834.9486$/h) i.e. by 4.29% compared with CASE 1, and the results obtained are compared with other techniques as shown in Table 4.
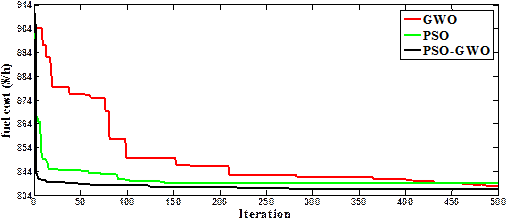
Figure 6. Convergent curves of Case 5
Case 6: Minimization of real power loss
In this case, the purpose of the OPF problem is to minimize power losses; the real power loss to be minimized is formulated as follows, Eq. (34):
![]() (34)
(34)
Where: ![]() is the difference in
voltage angles between bus 𝑖
and bus 𝑗 and
is the difference in
voltage angles between bus 𝑖
and bus 𝑗 and ![]() is transfer
conductance.
is transfer
conductance.
The tendency to decrease the objective function of total real power transmission loss using the PSO-GWO technique appears Figure 7. The optimal settings of the control variables are presented in Table 3 in this case 6 by PSO-GWO result in real power losses of 2.8946 MW, better than all the results summarized in Table 4.
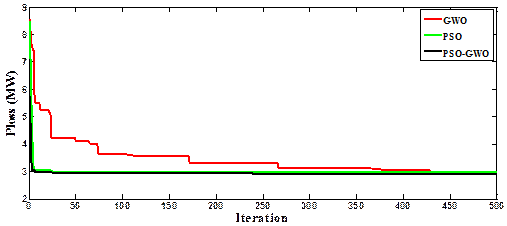
Figure 7. Convergent curves of Case 6
Conclusions
In this article, a new Hybrid technique called PSO-GWO is applied to solve OPF problems. One test system and six cases have been studied in order to evaluate the performance of the suggested technique. The OPF problem was reported as a non-linear optimization problem with equality and inequality constraints. Where several objective functions have been considered to minimize the fuel cost, to improve the voltage profile, and to enhance the voltage stability. However, the yielded results have been compared to those yielded using standard optimization techniques such as PSO, GWO. The essential conclusion that can be extracted from this article is that the PSO-GWO is a very efficient and robust technique for solving OPF problems. It has perfect convergence characteristics and can be realized better effectiveness than some well-known optimization techniques. A comparison of the results yielded from PSO-GWO and other techniques confirm the superiority of the algorithm for the suggested PSO-GWO on stochastic methods in terms of solution efficiency for the OPF problems.
References
1. Cain M., O'Neill R., Castillo A., History of optimal power flow and formulations, FERC Staff Tech Pap; 2012. p. 1–36.
2. Hinojosa V.H., Araya R., Modelling a mixed-integer-binary small-population evolutionary particle swarm algorithm for solving the optimal power flow problem in electric power systems, Appl. Soft Comput. J., 2013, 13, p. 3839–3852.
3. Niknam T., Azizipanah-Abarghooee R., Narimani M.R., Reserve constrained dynamic optimal power flow subject to valve-point effects, prohibited zones and multi-fuel constraints, Energy, 2012, 47 (1):451e64.
4. Ambriz-Perez H., Acha E., Fuerte-Esquivel C.R., De La Torre A., Incorporation of a UPFC model in an optimal power flow using Newton’s method, IEEE Proc Gener Transm Distrib., 1998, 145: 336e44.
5. Momoh J.A., El-Hawary M.E., Adapa R., A review of selected optimal power literature to 1993. Part II: Newton, linear programming and interior point methods, IEEE Trans Power Syst., 1999; 14:105e11.
6. Burchett R.C., Happ H.H., Vierath D.R., Quadratically convergent optimal power flow, IEEE Trans Power Appar Syst., 1984; 103 (11), p. 3267–76.
7. Niknam T. , Raoul Narimani M., Jabbari M., Malekpour A.R., A modified shuffle frog leaping algorithm for multi-objective optimal power flow, Energy, 2011, 36, p. 6420–6432.
8. Bouchekara H.R.E.H., Optimal power flow using black-hole-based optimization approach, Appl Soft Comput J., 2014, 24, p. 879–88.
9. Bouchekara H.R.E.H., Abido M.A., Chaib A.E., Mehasni R., Optimal power flow using the league championship algorithm: a case study of the Algerian power system, Energy Convers. Manag., 2014, 87, p. 58–70.
10. Bhattacharya A., Roy P.K., Solution of multi-objective optimal power flow using gravitational search algorithm, IET Gener. Transm. Distrib., 2012, p. 751–763.
11. Khorsandi A., Hosseinian S.H., Ghazanfari A., Modified artificial bee colony algorithm based on fuzzy multi-objective technique for optimal power flow problem, Electr. Power Syst. Res., 2013, 95, p. 206–13.
12. Daryani N., Hagh M.T., Teimourzadeh S., Adaptive group search optimization algorithm for multi-objective optimal power flow problem, Appl. Soft Comput., 2016, 38, p. 1012–1024.
13. Ghasemi M., Ghavidel S., Ghanbarian M.M., Massrur H.R., Gharibzadeh M., Application of imperialist competitive algorithm with its modified techniques for multi-objective optimal power flow problem: a comparative study, INF Sci (Ny), 2014, 281, p. 225–47.
14. Bouchekara HRE-H, Abido M.A., Optimal power flow using differential search algorithm, Electr Power Components Syst., 2014, 42, p. 1683–99.
15. Bouchekara H.R.E.H., Abido M.A., Boucherma M., Optimal power flow using teaching-learning-based optimization technique, Electr. Power Syst. Res., 2014, 114, p. 49–59.
16. Mukherjee A., Mukherjee V., Solution of optimal power flow using chaotic krill herd algorithm, Chaos, Solitons Fract., 2015, 78, p. 10–21.
17. Rao B.S., Vaisakh K., Multi-objective adaptive clonal selection algorithm for solving optimal power flow considering multi-type FACTS devices and load uncertainty, Appl. Soft Comput., 2014, 23, p. 286–297.
18. Mirjalili S., Lewis A., Adaptive gbest-guided gravitational search algorithm, Neural Comput Appl., 2014, 25 (7–8), p. 1569–1584.
19. Dhillon J.S., Kothari D.P., Power system optimization, 2nd edn. PHI, New Delhi, 2010.
20. Mirjalili S., Mirjalili V., Lewis A., Grey wolf optimizer, Adv. Eng. Softw., 2014, 69, p. 46–61.
21. Chaib A.E., Bouchekara H.R.E.H., Mehasni R., Abido M.A., Optimal power flow with emission and non-smooth cost functions using backtracking search optimization algorithm, Int. Journal of Electrical Power & Energy Systems, 2016, 81, p. 64-77.
22. Yohannes M.S., Solving economic load dispatch problem using particle swarm optimization technique, International Journal of Intelligent Systems and Applications (IJISA), 2012, 4 (12), 12.
23. Mirjalili S., Mirjalili S.M., and Lewis A., Grey wolf optimization, Advances in Engineering Software, 2014, 69, p. 46-61.
24. Sharma S., Mehta S, Chopra N., Economic load dispatch using grey wolf optimization, International Journal Of Engineering Research and Applications(IJERA),ISSN:2248- 9622, 2015, 5 (4).
25. Vikram K.K., A novel hybrid PSO–GWO approach for unit commitment problem, Neural Computing and Applications, Springer, 2015.
26. Abido M.A., Optimal power flow using particle swarm optimization, Int. J. Electr. Power Energy Syst., 2002, 24 (7), p. 563–571.
27. Abou El Ela A.A., Abido M.A., Optimal power flow using differential evolution algorithm, Electr. Power Syst. Res., 2010, 80 (7), p. 878–885.
28. Kessel P., Glavitsch H., Estimating the voltage stability of a power system, IEEE Trans Power Deliv., 1986, 1, p. 346–54.
29. Abou El Ela A.A., Abido M.A., Spea S.R., Optimal power flow using differential evolution algorithm, Electr. Power Syst. Res., 2010, 80, p. 878–85.
30. Hardiansyah H., A modified particle swarm optimization technique for economic load dispatch with valve-point effect, Int. J. Intell Syst. Appl., 2013, 5, p. 32–41.
31. Ghasemi M., Ghavidel S., Ghanbarian M.M., Gitizadeh M., Multi-objective optimal electric power planning in the power system using Gaussian bare-bones imperialist competitive algorithm, Inf. Sci., 2015, 294, p. 286–304.
32. Adaryani M.R., Karami A., Artificial bee colony algorithm for solving multi-objective optimal power flow problem, Int. J. Electr. Power Energy Syst., 2013, 53, p. 219–230.
33. Niknam T., Narimani M.R., Azizipanah-Abarghooee R., A new hybrid algorithm for optimal power flow considering prohibited zones and valve point effect, Energy Convers. Manage., 2012, 58, p. 197–206.
34. Vaisakh K., Srinivas L.R. Evolving ant direction differential evolution for OPF with non-smooth cost functions, Engineering Applications of Artificial Intelligence, 2011, 24, p. 426–436.
35. Bouchekara H.R.E.H., Abido M.A., Chaib A.E., Optimal power flow using an improved electromagnetism-like mechanism method, Electric Power Components and Syst., 2016.
36. Bouchekara H.R.E.H., Chaib A.E., Abido M.A., El-Sehiemy R.A., Optimal power flow using an improved colliding body’s optimization algorithm, Applied Soft Computing, 2016, 42, p. 119-131.
37. Kumar A.R., Premalatha L., Optimal power flow for a deregulated power system using adaptive real coded biogeography-based optimization, Electr. Power Energy Syst., 2015, 73, p. 393–399.
38. Roy R., Jadhav H.T., Optimal power flow solution of power system incorporating stochastic wind power using Gbest guided artificial bee colony algorithm, Electrical Power and Energy Systems, 2015, 64, p.562–578.
39. Mohamed A.A.A., Mohamed Y.S., El-Gaafary A.A., Hemeida A.M., Optimal power flow using moth swarm algorithm, Electric Power Systems Research, 2017, 142, p. 190-206.
40. Dilip L., Bhesdadiya R., Jangir P., Optimal power flow problem solution using multi-objective grey wolf optimizer algorithm, Springer Nature Singapore, Pte. Ltd., 2018.